La Crittografia Simmetrica – I Campi di Galois e i Cifrari a Flusso

La crittografia è la scienza che si occupa di cifrare e decifrare i dati, in modo da garantire la protezione e riservatezza delle informazioni. La cifratura è la trasformazione del messaggio (o testo) in chiaro in testo cifrato, mentre la decifratura consiste nel ricostruire il testo in chiaro a partire dal testo cifrato.
La crittografia è divisa in due branche fondamentali: la crittografia simmetrica e la crittografia asimmetrica.

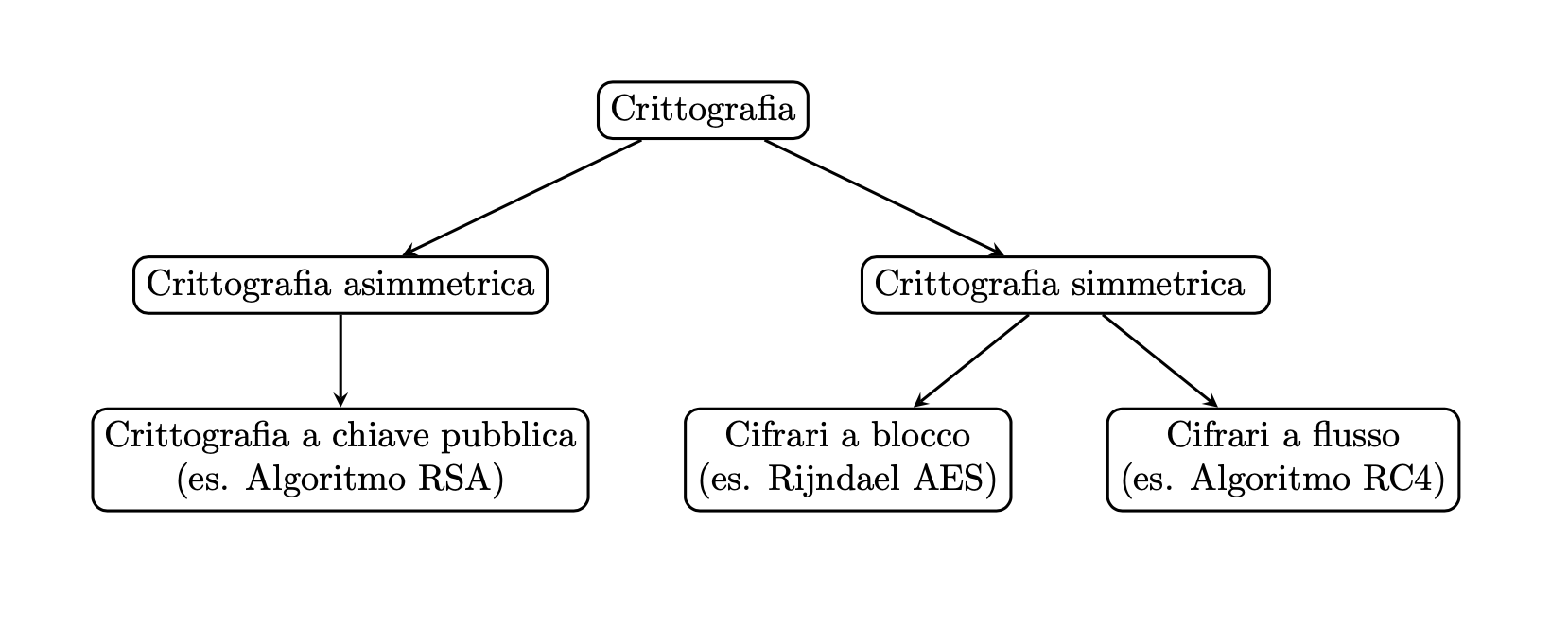
La crittografia simmetrica è suddivisa a sua volta in due grandi categorie: cifrari a flusso e cifrari a blocco. In questo articolo ci occuperemo dei cifrari a flusso. Per descrivere questo tipo di cifrari studieremo in particolare la teoria matematica dei campi finiti, chiamati anche campi di Galois, in onore del grande matematico francese Évariste Galois (1811-1832). Questa branca della matematica ha importanti applicazioni nella crittografia e in altri settori delle scienze dell’informazione e dell’ingegneria.

1) La crittografia simmetrica

Come è noto, la crittografia simmetrica è basata sull’utilizzo di una stessa chiave da parte del mittente e del destinatario del messaggio. La chiave rappresenta l’informazione segreta condivisa fra le parti, che intendono scambiare le informazioni in modalità riservata. Un sistema di crittografia simmetrica utilizza due funzioni fondamentali:

\[ \begin{array}{l} c = e(k,m) \quad \text{ cifratura } \\ m = d(k,c) \quad \text{decifratura } \\ \end{array} \]

dove

• \(m\) è il messaggio in chiaro
• \(c\) è il messaggio cifrato
• \(k\) è la chiave segreta
• \(e\) è la funzione di cifratura
• \(d\) è la funzione di decifratura

Indichiamo con \(M\) lo spazio dei messaggi in chiaro possibili, con \(C\) l’insieme di tutti i messaggi cifrati e con \(K\) l’insieme di tutte le possibili chiavi, cioè lo spazio delle chiavi. Possiamo dare questa definizione formale di sistema crittografico:

Definizione 1.1
Un cifrario simmetrico definito sugli spazi \((M,K,C)\) è una coppia di algoritmi (o funzioni) \(e,d\), così definiti:

\[ \begin{array}{l} e: K \times M \to C \quad \text{cifratura} \\ d: K \times C \to M \quad \text{decifratura} \end{array} \]

Le due funzioni devono verificare la seguente condizione di coerenza:

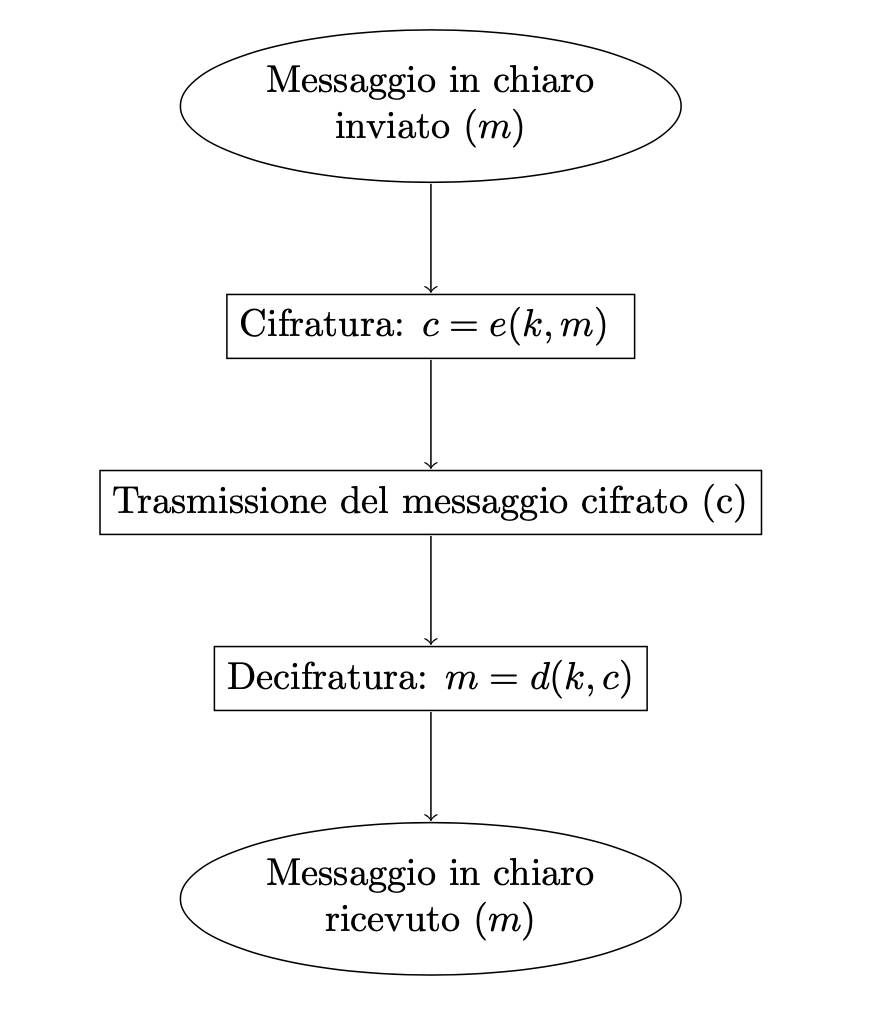
\[ \begin{array}{l} d (k,e(k,m)) = m \quad \forall k \in K, m \in M \end{array} \]

Il diagramma seguente evidenzia le principali operazioni nei processi di cifratura e decifratura:

In base al principio di Kerckhoff (vedi articolo su questo sito) le funzioni di cifratura e decifratura dovrebbero essere rese pubbliche. L’unica parte segreta è la chiave \(k\), la quale deve essere conosciuta dal mittente e dal destinatario.
Naturalmente una condizione necessaria per avere un sistema difficile da attaccare è che lo spazio delle chiavi \(K\) sia abbastanza grande, altrimenti si potrebbe capire il funzionamento mediante una ricerca esaustiva delle chiavi possibili.
Per comprendere il funzionamento dei moderni sistemi crittografici è necessario conoscere le teorie matematiche che sono alla base degli algoritmi: algebra, teoria dei numeri, probabilità, generazione di numeri casuali, ecc. Di seguito introduciamo alcuni concetti di algebra astratta e in particolare le proprietà dei campi finiti, che hanno un ruolo fondamentale negli algoritmi utilizzati nei cifrari a flusso.

2) Le strutture algebriche fondamentali: gruppi, anelli e campi

Un insieme è una collezione di oggetti che vengono chiamati gli elementi dell’insieme. La teoria degli insiemi è la branca della matematica che studia gli insiemi e le loro proprietà. Le strutture algebriche sono definite associando agli insiemi delle opportune operazioni o trasformazioni. Le strutture base dell’algebra sono i gruppi, gli anelli e i campi. Esempi classici di strutture algebriche sono gli insiemi di numeri interi, razionali, reali e complessi, con le usuali operazioni di addizione e moltiplicazione.
Per definire una struttura algebrica su un insieme generico introduciamo il concetto di operazione binaria.

Definizione 2.1
Sia dato un insieme \(A\). Una operazione binaria è una funzione

\[ \begin{array}{l} f: A \times A \to A \\ f: (a,b) \to f(a,b) \end{array} \]

che ad ogni coppia di elementi di \(A\) assegna un valore sempre dell’insieme \(A\) (proprietà di chiusura). Possiamo indicare l’operazione binaria con un simbolo qualsiasi, ad esempio

\[ *: (a,b) \to a * b \]

Tuttavia in genere utilizzeremo il simbolo moltiplicativo \(\cdot\), tranne nel caso di gruppi additivi per i quali useremo il simbolo \(+\).
Nel seguito descriveremo brevemente le tre strutture algebriche più importanti: i gruppi, gli anelli e i campi.

2.1) Gruppi

Un gruppo è una coppia ordinata \((G,\cdot)\) dove \(G\) è un insieme e \(\cdot\) è un’operazione binaria su \(G\), che ad ogni coppia di elementi di \(G\) associa un elemento di \(G\) e verifica le seguenti proprietà (o assiomi):

• proprietà associativa: \(a \cdot (b \cdot c)=(a \cdot b) \cdot c\)
• elemento neutro: esiste un elemento \(e\) di \(G\) tale che \(a \cdot e=a\) per ogni \(a \in G\)
• elemento inverso: per ogni elemento \(a \in G\) esiste un elemento \(b\) tale che \(a \cdot b=e\)

Un gruppo si dice commutativo, o abeliano in onore del grande matematico norvegese N.H. Abel (1802-1829), se risulta

\[ a \cdot b = b \cdot a \quad \forall a,b \in G \]

L’elemento neutro \(e\) viene indicato in genere con \(1\) nel caso di gruppi moltiplicativi, con \(0\) nel caso di gruppi additivi. L’inverso di un elemento \(a\) viene indicato con \(a^{-1}\) nel caso di gruppi moltiplicativi e con \(-a\) nel caso di gruppi additivi.
In genere si aggiunge un quarto assioma, imponendo che l’elemento dell’operazione binaria \(a \cdot b\) debba appartenere all’insieme \(G\); tuttavia questo assioma è chiaramente superfluo, in quanto è già implicito nella definizione di operazione binaria.
Si chiama ordine di un gruppo il numero di elementi dell’insieme \(G\) e si indica con il simbolo \(|G|\).

Esempio 2.1
L’insieme degli interi \(\mathbb{Z}\) con l’operazione di addizione è un gruppo additivo, di ordine infinito. Con l’operazione di moltiplicazione non è un gruppo, in quanto l’inverso moltiplicativo di un intero \(x\) non esiste, tranne nel caso \(x= \pm 1\).
L’insieme dei numeri naturali non è un gruppo con l’operazione binaria di addizione, in quanto non esistono gli inversi additivi dei numeri naturali. Naturalmente non è un gruppo neanche rispetto alla moltiplicazione.

Esempio 2.2
L’insieme dei numeri razionali \(\mathbb{Q}\) con l’operazione di addizione è un gruppo additivo.
Con l’operazione di moltiplicazione non è un gruppo in quanto il numero \(0\) non ha un inverso. Tuttavia, se togliamo lo zero allora l’insieme \(\mathbb{Q}^{*}=\mathbb{Q}\setminus 0\) è un gruppo moltiplicativo.
Considerazioni simili si possono fare per gli insiemi dei numeri reali \(\mathbb{R}\) e dei numeri complessi \(\mathbb{C}\).

Esercizio 2.1
Dimostrare che l’insieme dei numeri complessi \(G=\{1,-1,i,-i\}\) è un gruppo con l’operazione di moltiplicazione. Determinare l’elemento neutro e per ogni elemento del gruppo trovare il suo inverso.

Ricordiamo la definizione di relazione di congruenza fra due interi. Sia \(n\) un intero non nullo e siano \(a,b\) due interi qualsiasi. Si dice che \(a\) è congruente a \(b\) modulo \(n\), e si scrive \(a \equiv b \pmod{n}\), se e solo se risulta

\[ n | b-a \quad \text{cioè} \quad b-a=kn \ , \quad k \in \mathbb{Z} \]

La relazione di congruenza è una relazione di equivalenza (riflessiva, simmetrica e transitiva), che induce una partizione dell’insieme degli interi in \(n\) classi di equivalenza disgiunte.

Esercizio 2.2 – Il gruppo additivo delle classi di congruenza
Indichiamo con \(\mathbb{Z}_{n}\) l’insieme costituito dalle classi di congruenza modulo \(n\). L’insieme contiene \(n\) elementi o classi. Ogni classe relativa ad un intero \(a\) è così definita:

\[ \overline{a}=\{x \in \mathbb{Z}: x \equiv a \pmod{n} \} \]

Sostanzialmente la classe \(\overline{a}\) contiene tutti gli interi che danno lo stesso resto di \(a\) nella divisione per \(n\). Ovviamente sono possibili solo \(n\) resti diversi. Ad esempio la classe \(\overline{0}\) contiene lo zero e tutti i multipli positivi e negativi di \(n\).
Sull’insieme delle \(n\) classi definiamo questa operazione binaria di addizione:

\[ \overline{a}+ \overline{b}= \overline{a+b} \]

Esercizio 2.3
Dimostrare in primo luogo che l’operazione è ben definita, cioè il risultato non dipende dall’elemento che si prende come rappresentante di una data classe. Quindi dimostrare che con questa operazione l’insieme diventa un gruppo abeliano.
Il gruppo delle classi di congruenza modulo \(n\) viene anche indicato con il simbolo \(\mathbb{Z}/n\mathbb{Z}\) o più semplicemente con \(\mathbb{Z}_{n}\).

Esempio 2.3
Nell’insieme \(\mathbb{Z}_{n}\) possiamo definire anche una operazione di moltiplicazione fra le classi residuo. Date due classi \(\overline{a},\overline{b}\), l’operazione è così definita:

\[ \overline{a}\cdot \overline{b}= \overline{a \cdot b} \]

È facile verificare che l’operazione è ben definita, cioè il risultato non dipende dall’elemento che si prende come rappresentante di una data classe. L’insieme \(\mathbb{Z}_{n}\) non è un gruppo con l’operazione di moltiplicazione, in quanto la classe \(\overline{0}\) non ha un inverso. Tuttavia, anche prendendo l’insieme \(\mathbb{Z}_{n}\setminus{0}\) in generale non abbiamo un gruppo, in quanto non sempre esiste l’inverso moltiplicativo.
Ad esempio se \(n=6\) solo \(1\) e \(5\) hanno l’inverso moltiplicativo. Infatti \(1^{-1}=1\) e \(5^{-1}=5\). Il numero \(2\) non ha inverso moltiplicativo modulo \(6\), in quanto non esiste alcun intero \(x\) tale che \(2x \equiv 1 \pmod{6}\), come è facile verificare. Lo stesso vale per i numeri \(3,4\).
L’esistenza dell’inverso moltiplicativo di una classe è determinata dal seguente teorema:

Teorema 2.1
Un elemento \(a\) ha un inverso moltiplicativo \(b\), cioè \(ab \equiv 1 \pmod{n}\), se e solo se \((a,n)=1\).

Questo teorema deriva direttamente dal teorema di Bézout (vedi articolo) e dal piccolo teorema di Fermat (vedi articolo), che ricordiamo:

Teorema 2.2 – Fermat
Se \(p\) è un numero primo e \(a\) un intero, allora:

\[ a^{p} \equiv a \pmod{p} \]

Il teorema può essere scritto nella seguente forma:

\[ a^{p-1} \equiv 1 \pmod{p} \quad \text{se }(a,p)=1 \]

Da questo segue che se \((a,p)=1\) allora esiste l’inverso moltiplicativo di \(a\). Basta porre \(x=a^{p-2}\).

Esempio 2.4
Supponiamo \(a=17\) e \(n=36\). Abbiamo \((17,36)=1\). Per calcolare l’inverso moltiplicativo si può utilizzare l’algoritmo di Euclide. Tuttavia nei casi semplici si può determinare per tentativi. Ad esempio l’inverso moltiplicativo di \(17\) è uguale a \(17\) stesso, in quanto \(17 \cdot 17 = 289 = 36*8 +1\), e quindi

\[ 17 \cdot 17 \equiv 1 \pmod{36} \]

Indichiamo con \(\mathbb{Z}_{n}^{*}\) l’insieme delle classi residuo che hanno inverso moltiplicativo, cioè l’insieme delle classi \(\overline{a}\) tali che \((a,n)=1\). Tale insieme è un gruppo abeliano moltiplicativo. L’unità del gruppo è la classe \(\overline{1}\). Il numero degli elementi del gruppo \(\mathbb{Z}_{n}^{*}\) viene indicato con il simbolo \(\varphi(n)\), chiamata funzione di Eulero (vedi articolo).

Esempio 2.5 – Tabella moltiplicativa di \(\mathbb{Z}_{15}^{*}\)
Verificare la seguente tabella di Cayley per le operazioni del gruppo \(\mathbb{Z}_{15}^{*}\).

\[ \begin{array}{r|rrrrrrrr} \hline \times\quad & 1 & 2 & 4 & 7 & 8 & 11 &13 & 14\\ \hline 1 \quad & 1 & 2 & 4 & 7 & 8 & 11 &13 & 14\\ \hline 2 \quad & 2 &4 & 8 & 14 & 1 & 7 &11 & 13\\ \hline 4 \quad & 4 &8 & 1 & 13 & 2 & 14 &7 & 11\\ \hline 7 \quad & 7 &14 & 13 & 4 & 11 & 2 &1 & 8\\ \hline 8 \quad & 8 &1 & 2 & 11 & 4 & 13 &14 & 7\\ \hline 11 \quad & 11 &7 &14 & 2 & 13 & 1 &8 & 4\\ \hline 13 \quad & 13 &11 &7 & 1 & 14 & 8 &4 & 2\\ \hline 14 \quad & 14 &13 & 11 & 8 & 7 & 4 &2 & 1\\ \hline \end{array} \]

Esercizio 2.4
Trovare gli inversi moltiplicativi degli elementi del gruppo \(\mathbb{Z}_{11}^{*}\), cioè di \(\{1,2,3,4,5,6,7,8,9,10\}\).
Ad esempio l’inverso di \(9\) è \(5\), in quanto \(9 \cdot 5 \equiv 1 \pmod{11}\).

Definizione 2.2
Un sottoinsieme \(H\) di \(G\) è un sottogruppo di \((G,\cdot)\) se i suoi elementi formano un gruppo con la stessa operazione binaria.

È facile dimostrare che un sottoinsieme non vuoto \(H\) è un sottogruppo di \(G\) se e solo se risulta

\[ a \cdot b^{-1} \in H \quad \forall a,b \in H \]

Ricordiamo l’importante teorema di Lagrange:

Teorema 2.3 – Lagrange
Se \(H\) è un sottogruppo di \(G\) allora

\[ |G| = n |H| \ , \quad n \text{ intero positivo} \]

La teoria dei gruppi è una branca della matematica molto bella e molto vasta. Per uno studio approfondito vedere ^[1] oppure ^[2].

2.2) Anelli

Sia dato un insieme non vuoto \(R\)  sul quale sono definite due operazioni binarie chiuse, che indicheremo con \(+\) (addizione) e \(\cdot\) (moltiplicazione). La struttura \(R(+,\cdot)\) è un anello se soddisfa i seguenti assiomi:

• \(R(+)\) è un gruppo abeliano rispetto alla addizione
• \(a \cdot (b \cdot c)=(a \cdot b) \cdot c \quad\) (proprietà associativa)
• \(a \cdot (b+c)= (a \cdot b) + ( a \cdot c) \quad\) (proprietà distributiva)

Per il gruppo abeliano usiamo la notazione \(+\) per indicare l’operazione binaria, l’elemento neutro viene indicato con il simbolo \(0\). L’inverso di un elemento \(a\) è indicato con il simbolo \(-a\) e viene chiamato anche l’opposto di \(a\).
Un anello si dice commutativo se risulta

\[ a \cdot b = b \cdot a \quad \forall a,b \in R \]

Un anello si dice dominio di integrità se non ha divisori dello zero, cioè se

\[ a \cdot b = 0 \implies a=0 \lor b = 0 \]

Esercizio 2.5
Dimostrare che in un dominio di integrità vale la legge di cancellazione del prodotto:

\[ c \neq 0 \land (a \cdot c = b \cdot c) \quad \implies a = b \]

Esercizio 2.6
Dimostrare che in un anello vale la legge dei segni:

\[ (-a)\cdot (-b) = a \cdot b \]

Un anello \(R\) si dice anello unitario se esiste un elemento, che chiamiamo elemento unità e indichiamo con \(1\), tale che

\[ a \cdot 1 = 1 \cdot a = a \quad \forall a \in R \]

L’elemento unità se esiste è unico, come è facile verificare.
In un anello con unità, un elemento \(a\) si dice una unità se esiste un altro elemento \(b\) tale che \(a \cdot b = 1\). L’elemento \(b\) si chiama l’inverso moltiplicativo di \(a\) e si indica con \(a^{-1}\).

Esempio 2.6
L’insieme degli interi \(\mathbb{Z}(+,\cdot)\) è un anello commutativo, con le operazioni di addizione e moltiplicazione. L’elemento neutro rispetto all’addizione è lo zero. L’unità moltiplicativa è il numero 1. Inoltre \(Z(+,\cdot)\) è un dominio di integrità, in quanto non esistono divisori dello zero.

Esercizio 2.7 – L’anello delle classi di congruenza
Dimostrare che l’insieme \(\mathbb{Z}_{n}\) con le operazioni di somma e prodotto definite in precedenza è un anello commutativo con unità. L’unità è la classe \(\overline{1}\).

Esercizio 2.8
Dimostrare che in generale l’anello \(\mathbb{Z}_{n}\) non è un dominio di integrità. Cioè possono esistere due classi non nulle \(\overline{a},\overline{b}\) tali che \(\overline{a} \cdot \overline{b}=\overline{0}\).

Suggerimento
Considerare ad esempio le due classi \(\overline{2}\) e \(\overline{3}\) nell’anello \(\mathbb{Z}_{6}\).

Per semplicità spesso una classe si indica con il simbolo \(a\) al posto del simbolo \(\overline{a}\).

Esempio 2.7 – L’anello dei polinomi coefficienti interi
Indichiamo con \(\mathbb{Z}[x]\) l’insieme di tutti i polinomi a coefficienti interi nella variabile \(x\). Un polinomio \(f(x) \in \mathbb{Z}[x]\) se e solo se

\[ f(x) = a_{0} + a_{1}x + a_{2}x^{2} + \cdots a_{n}x^{n} \ , \quad n \ge 0 \ , \quad a_{k} \in \mathbb{Z} \]

Se \(a_{n} \neq 0\) allora il polinomio si dice di \(\textbf{grado}\) \(n\), e si scrive \(\deg f(x)=n\). Il polinomio i cui coefficienti sono tutti nulli viene chiamato polinomio zero.
Un polinomio può anche essere rappresentato da una serie infinita

\[ f(x)=\sum\limits_{k=0}^{\infty}a_{k}x^{k} \]

con l’intesa che solo un numero finito di coefficienti è diverso da zero.
Sull’insieme dei polinomi \(\mathbb{Z}[x]\) possiamo definire due operazioni binarie di addizione e moltiplicazione. Dati due polinomi \( f(x) = \sum\limits_{k=0}^{\infty}a_{k}x^{k},\ g(x) = \sum\limits_{k=0}^{\infty}b_{k}x^{k}\) abbiamo

\[ \begin{array}{l} \displaystyle f(x) + g(x) = \sum\limits_{k=0}^{\infty}(a_{k}+b_{k})x^{k} \\ \displaystyle f(x) \cdot g(x) = \sum\limits_{k=0}^{\infty}c_{k}x^{k} \ , \quad c_{k}=\sum\limits_{i=0}^{k}a_{i}b_{k-i} \end{array} \]

Esercizio 2.9
Dimostrare che con queste operazioni \(\mathbb{Z}[x]\) è un anello commutativo. Inoltre è anche un dominio di integrità.

Al posto dell’anello degli interi \(\mathbb{Z}\) si può utilizzare qualsiasi altro anello \(R\) e definire l’anello \(R[x]\) dei polinomi corrispondenti. Si può dimostrare che l’anello \(R[x]\) è commutativo se e solo se \(R\) è commutativo. Inoltre \(R[x]\) è un dominio di integrità se e solo se anche \(R\) è un dominio di integrità.
Come per gli interi, anche per i polinomi possiamo introdurre la relazione di divisibilità. Un polinomio \(f(x)\) è divisibile da un polinomio \(g(x)\) non identicamente nullo, se esiste un polinomio \(q(x)\) tale che

\[ f(x)=q(x)g(x) \ , \quad f(x),g(x),q(x) \in R[x] \]

Indichiamo la relazione di divisibilità con la notazione \(g(x) \mid f(x)\).
Il concetto di congruenza può essere esteso anche ai polinomi. Dati tre polinomi \(f(x),g(x),q(x) \in R[x]\), si dice che \(f(x)\) è congruente a \(g(x)\) modulo \(h(x)\) se \(h(x)\) divide la differenza \(f(x)-g(x)\). Formalmente

\[ f(x) \equiv g(x) \pmod{h(x)} \iff h(x)|f(x) – g(x) \]

Esercizio 2.10
Dimostrare che la relazione di congruenza fra polinomi è una relazione di equivalenza, cioè è riflessiva, simmetrica e transitiva.

Possiamo quindi definire le classi di congruenza in modo analogo a quanto fatto per l’anello dei interi. Ad esempio la classe di equivalenza modulo \(h(x)\) associata ad un polinomio \(f(x)\) è

\[ \overline{f(x)}=\{g(x) \in R[x]: g(x) \equiv f(x) \pmod{h(x)}\} \]

Fissato un polinomio \(h(x)\), mediante la relazione di congruenza modulo \(h(x)\) l’anello dei polinomi \(R[x]\) può essere partizionato in classi di equivalenza. Possiamo quindi definire l’anello quoziente rispetto alla congruenza modulo \(h(x)\), indicato con \(R[x]/h(x)\),

\[ R[x]/h(x)= \{\overline{f(x)},\overline{g(x)}, \cdots \} \]

dove

\[ \overline{f(x)}=\{f(x) + \lambda(x) \cdot h(x): \quad \lambda(x) \in R[x]\} \]

Esempio 2.8
Consideriamo l’anello dei polinomi a coefficienti razionali: \(\mathbb{Q}[x]\). Allora se \(h(x)=x^{2}-2 \in \mathbb{Q}[x]\) abbiamo

\[ \mathbb{Q}[x]/(x^{2}-2) = \{ax+b: a,b \in \mathbb{Q}\} \]

In questo esempio ogni polinomio di qualunque grado viene ridotto ad un polinomio di primo grado, sostituendo ogni potenza \(x^{2}\) con \(2\).

2.3) Campi

Un campo è un insieme \(F\) sul quale sono definite due operazioni binarie \(+,\cdot\) tali che:

• \(F(+)\) è un gruppo abeliano. L’elemento neutro viene indicato con \(0\) e l’inverso additivo di \(a\) con \(-a\);
• \(F \setminus \{0\}(\cdot)\) è un gruppo abeliano. L’elemento neutro viene indicato con \(1\) e l’inverso moltiplicativo di \(a\) con \(a^{-1}\);
• vale la legge di distribuzione: \(a\cdot(b+c)=a \cdot b + a \cdot c\).

Un campo può essere finito o infinito. Nel caso finito, un campo di ordine \(n\) viene in genere indicato con \(F_{n}\), oppure con \(GF(n)\) in onore del matematico francese Galois.

Esempio 2.9
Sono campi le seguenti strutture algebriche:

\[ \begin{array}{l} \mathbb{Q}(+,\cdot) \quad \text{campo dei numeri razionali} \\ \mathbb{R}(+,\cdot) \quad \text{campo dei numeri reali} \\ \mathbb{C}(+,\cdot) \quad \text{campo dei numeri complessi} \\ \end{array} \]

Esercizio 2.11
Dimostrare che il seguente insieme:

\[ \mathbb{Q}(\sqrt{2}) =\{a + b \sqrt{2}: a,b \in \mathbb{Q}\} \]

è un campo, con le normali operazioni di addizione e moltiplicazione di numeri reali.
Un modo equivalente di studiare il campo \(\mathbb{Q}(\sqrt{2})\) è il seguente. Il valore \(\sqrt{2}\) è una radice del polinomio \(x^{2}- 2=0.\) Possiamo quindi considerare l’anello quoziente

\[ \mathbb{Q}[x] / (x^{2}-2) \]

Questo anello in realtà è un campo, isomorfo (cioè equivalente dal punto di vista algebrico) al campo \(\mathbb{Q}(\sqrt{2})\). L’isomorfismo è dato dalla seguente corrispondenza:

\[ a + bx \iff a + b \sqrt{2} \ ,\quad a,b \in \mathbb{Q} \]

Esempio 2.10
Consideriamo l’anello dei polinomi a coefficienti interi: \(\mathbb{Z}[x]\). Se \(h(x)=x^{2}+1\) allora l’anello quoziente è equivalente agli interi di Gauss, cioè l’insieme dei numeri complessi \(z=a+bi\), dove \(a,b\) sono interi (vedi articolo).

Definizione 2.3 – Sottocampo
Sia \(F\) un campo. Un sottoinsieme \(S \subset F\) è un sottocampo di \(F\) se anche esso è un campo con le stesse operazioni di \(F\). Se \(F\) è un sottocampo di un campo \(K\), allora si dice che \(K\) è una estensione di \(F\).
Ad esempio \(\mathbb{Q}\) è un sottocampo di \(\mathbb{R}\). Inoltre \(\mathbb{R}\) è un sottocampo di \(\mathbb{C}\).

Esercizio 2.12
Se \(K\) è un campo, dimostrare che l’intersezione di tutti i suoi sottocampi è un campo.

2.4) Spazi vettoriali

Uno spazio vettoriale su un un campo \(F\), i cui elementi vengono chiamati scalari, è un insieme non vuoto \(V\), i cui elementi sono chiamati vettori, nel quale sono definite due operazioni di somma di due vettori e di moltiplicazione di un vettore per uno scalare:

\[ \begin{array}{l} +: V \times V \to V \ ,\quad (u,v) \to u+v \\ \cdot: F \times V \to V \ ,\quad (\alpha,v) \to \alpha \cdot v \end{array} \]

Inoltre devono essere verificate le seguenti proprietà (per semplicità indichiamo l’operazione di prodotto scalare semplicemente con \(\alpha v\)):

\[ \begin{array}{l} V(+) \quad \text{è un gruppo abeliano} \\ \alpha (u+v) = \alpha u + \alpha v \\ (\alpha + \beta)v = \alpha v + \beta v \\ (\alpha \beta)v= \alpha (\beta v) \end{array} \]

Esercizio 2.13
Dimostrare che

\[ \begin{array}{l} 1 \cdot v = v \quad \forall v \in V \\ 0 \cdot v = 0 \quad \forall v \in V \\ \end{array} \]

Base e dimensione di uno spazio vettoriale
Sia \(B=\{v_{1},v_{2}, \cdots,v_{n}\}\) un insieme di vettori di uno spazio vettoriale \(V\) su un campo \(F\). Si chiama combinazione lineare di vettori l’espressione

\[ v = a_{1}v_{1}+ \cdots + a_{n}v_{n} \ ,\quad a_{i} \in F \]

I vettori \(v_{1},v_{2}, \cdots,v_{n}\) si dicono liberamente indipendenti se la combinazione lineare è nulla se e solo se tutti i coefficienti \(a_{i}\) sono uguali a zero. Altrimenti si dicono linearmente dipendenti.

Definizione 2.4 – Base di uno spazio vettoriale
Un sottoinsieme \(B=\{v_{1},v_{2}, \cdots,v_{n}\}\) di uno spazio vettoriale \(V\) è una base dello spazio \(V\) se soddisfa alle seguenti condizioni:

• ogni vettore di \(V\) può essere espresso in modo unico come combinazione lineare dei vettori di \(B\);
• i vettori di \(B\) sono liberamente indipendenti.

Ogni spazio vettoriale ha una base, che può essere finita o infinita. Per uno spazio vettoriale possono essere scelte diverse basi, che tuttavia hanno lo stesso numero di elementi. Il numero di elementi della base si chiama dimensione dello spazio vettoriale.

Esempio 2.11
L’esempio base di spazio vettoriale su un campo \(F\) è dato dal prodotto cartesiano

\[ F^{n}=\{(a_{1}, a_{2}, \cdots, a_{n}), a_{i} \in F\} \]

Dati due vettori \(a=(a_{1}, \cdots, a_{n})\), \(b=(b_{1}, \cdots, b_{n})\) e uno scalare \(\alpha \in F\) abbiamo

\[ \begin{array}{l} a+b= (a_{1}, \cdots, a_{n})+ (b_{1}, \cdots, b_{n}) = (a_{1}+ b_{1}, \cdots, a_{n}+b_{n}) \\ \alpha a= \alpha (a_{1}, \cdots, a_{n}) = (\alpha a_{1}, \cdots, \alpha a_{n}) \end{array} \]

La base canonica per lo spazio \(F^{n}\) è \(B=\{e_{1},e_{2}, \cdots,e_{n}\}\) dove

\[ \begin{array}{l} e_{1}=(1,0,0, \cdots,0) \\ e_{2}=(0,1,0, \cdots,0) \\ \vdots \\ e_{n}=(0,0,0, \cdots,1) \end{array} \]

Si può dimostrare che ogni spazio vettoriale \(V\) di dimensione finita \(n\) su un campo \(F\) è equivalente allo spazio \(F^{n}\), per una opportuna scelta di una base di \(V\).
Un campo può essere considerato come spazio vettoriale su uno dei suoi sottocampi. I vettori sono gli elementi del campo e gli scalari sono gli elementi del sottocampo. Se lo spazio vettoriale ha dimensione finita, allora la dimensione dello spazio vettoriale si chiama grado del campo rispetto al suo sottocampo.

Esercizio 2.14
Determinare le dimensioni dei seguenti spazi vettoriali:
1) spazio vettoriale di un campo su se stesso
2) spazio vettoriale dei numeri reali \(\mathbb{R}\) sul campo dei razionali \(\mathbb{Q}\)
3) spazio vettoriale dei numeri complessi \(\mathbb{C}\) sul campo dei numeri reali \(\mathbb{R}\)

3) Anello dei polinomi su un campo

In precedenza abbiamo introdotto l’anello \(R[x]\) dei polinomi nella variabile \(x\), definiti su un anello generico \(R\). Supponiamo ora che l’anello base sia un campo \(F\) e studiamo l’anello dei polinomi sul campo \(F[x]\). Il campo \(K\) può essere costituito dai razionali, reali, complessi, oppure può essere un campo finito. Un polinomio \(f(x) \in F[x]\) di grado \(n\) ha la seguente rappresentazione:

\[ f(x)=a_{0} + a_{1}x^{1}+ a_{2}x^{2}+ \cdots + a_{n}x^{n}=\sum\limits_{k=0}^{n}a_{k}x^{k} \ ,\quad a_{n} \neq 0 \]

dove i coefficienti \(a_{k},\ k=0,1,\cdots,n\) appartengono al campo \(F\). Se \(a_{n}=1\) il polinomio si chiama monico.

Esempio 3.1 – Polinomi sul campo \(F_{2}\)
Un polinomio nel campo finito \(F_{2}\) ha la stessa forma di un polinomio a coefficienti reali, ma i coefficienti assumono solo i valori \(0,1\). Ad esempio \(p(x)= x^{5}+ x^{2}+1\).
Diversamente dal caso reale, due polinomi diversi sul campo \(F_{2}\) possono rappresentare una stessa funzione, cioè assumono gli stessi valori. Ad esempio \(p(x)=x^{2}+x+1\) e \(q(x)=1\) assumono gli stessi valori.
Per i polinomi su un campo vale un algoritmo di divisione simile a quello degli interi.

Teorema 3.1 – Teorema di divisione dei polinomi
Siano dati due polinomi \(f(x),g(x) \in F[x]\), con \(g(x) \neq 0\). Allora esistono e sono unici due polinomi \(q(x),r(x) \in F[x]\) tali che

\[ f(x) = g(x)q(x) + r(x) \]

dove \(r(x)=0\) oppure il grado di \(r(x)\) è minore del grado di \(g(x)\).

Dimostrazione
Se \(f(x)=0\) oppure \(f(x)\) ha grado minore di \(g(x)\) basta definire \(q(x)=0\) e \(r(x)=f(x)\). Altrimenti si effettua la divisione fra i due polinomi con il metodo elementare per calcolare il quoziente \(q(x)\) e il resto \(r(x)\). Alla fine della divisione può risultare \(r(x)=0\) oppure il grado di \(r(x)\) è inferiore al grado di \(g(x)\).
Per dimostrare l’unicità della coppia \(q(x),r(x)\) supponiamo che esista un’altra decomposizione \(f(x) = g(x)q_{1}(x) + r_{1}(x)\). Allora avremo

\[ r(x) -r_{1}(x)=g(x)(q_{1}(x)-q(x)) \]

Questo implica che \(g(x)|(r(x)-r_{1}(x)\). Ma questo è possibile solo se \(r(x)-r_{1}(x)\) è identicamente nullo, in quanto il grado di \(g(x)\) è maggiore del grado di \(r(x)-r_{1}(x)\).

3.1) Massimo comune divisore e algoritmo di Euclide per i polinomi

Definizione 3.1 – Massimo comune divisore di due polinomi
Un polinomio \(d(x)\) si dice massimo comune divisore di due polinomi \(f(x),g(x) \in F[x]\) se:

• \(d(x) \mid f(x)\) e \(d(x) \mid g(x)\)
• \(d(x)\) è una combinazione lineare dei due polinomi
• ogni altro divisore comune dei due polinomi divide \(d(x)\)

Teorema 3.2
Siano dati due polinomi \(f(x),g(x) \in F[x]\), non identicamente nulli. Allora esiste il massimo comune divisore.

Dimostrazione
Grazie al teorema di divisione dei polinomi, possiamo definire l’algoritmo di Euclide per il calcolo del massimo comune divisore di due polinomi, in modo simile al caso degli interi. Infatti abbiamo

\[ f(x) = g(x)q(x) + r(x) \implies \text{mcd}(f(x),g(x))=\text{mcd}(g(x),r(x)) \]

Eseguendo successive divisioni il grado del polinomio resto diminuisce fino a diventare zero. A questo punto il massimo comune divisore dei polinomi iniziali è l’ultimo resto non nullo.

Esercizio 3.1
Determinare il massimo comune denominatore dei seguenti polinomi \(f(x),g(x) \in \mathbb{Q}[x]\):

\[ f(x) = x^{4}+3x^{3}-x^{2}-4x -3 \\ g(x) = 3x^{3} + 10x^{2}+ 2x -3 \]

Soluzione: [\(\text{mcd}= x+3\)]

Esercizio 3.2
Determinare il massimo comune denominatore dei seguenti polinomi \(f(x),g(x) \in \mathbb{Z}_{2}[x]\):

\[ f(x) = x^{5}+x^{4} + x^{2}+1 \\ g(x) = x^{4} + x^{2} + x +1 \]

Soluzione: [\(\text{mcd}=x+1\)]

3.2) Polinomi primi e irriducibili

Definizione 3.2
Sia \(F\) un campo. Un polinomio non nullo \(f(x)\) dell’anello \(F[x]\) si dice irriducibile se non può essere scritto come prodotto di due polinomi con coefficienti nel campo \(F\), entrambi di grado inferiore al grado di \(f(x)\).

Esempio 3.2
Il polinomio \(x^{2}-2\) è irriducibile su \(\mathbb{Q}[x]\).
Il polinomio \(x^{2}+1\) è irriducibile sul campo dei numeri reali, ma è riducibile sul campo dei numeri complessi, in quanto \(x^{2}+1=(x+i)(x-i)\).

Esercizio 3.3
Dimostrare che il polinomio \(p(x)=x^{2}+x+1\) è irriducibile su \(GF(2)[x]\).

I polinomi irriducibili hanno un ruolo simile a quello dei numeri primi sull’anello degli interi \(\mathbb{Z}\). Vale un teorema analogo al lemma di Euclide per gli interi.

Teorema 3.3
Se un polinomio irriducibile \(p(x)\) divide un prodotto \(f(x)g(x)\) di due polinomi, allora \(p(x) \mid f(x)\) oppure \(p(x) \mid g(x)\).

Dimostrazione
Se \(f(x)=0\) oppure \(g(x)=0\) il teorema è ovvio. Supponiamo ora nessuno dei due polinomi sia identicamente nullo. Supponiamo anche che \( p(x)\) non divide \( f(x)\), altrimenti avremmo finito. Poiché \((p(x),f(x))=1\) segue che esistono due polinomi \(F(x),G(x)\) tali che

\[ p(x)F(x)+f(x)G(x)=1 \]

Moltiplicando per \(g(x)\) abbiamo

\[ p(x)g(x)F(x)+f(x)g(x)G(x)=g(x) \]

Poiché \(p(x)|f(x)g(x)\) e naturalmente \(p(x)|p(x)g(x)F(x)\) si ha che \(p(x)|g(x)\).

Teorema 3.4 – Teorema fondamentale dell’aritmetica dei polinomi
Sia \(F\) un campo. Per ogni polinomio \(f(x) \in F[x]\) esiste una fattorizzazione

\[ f(x) = k p_{1}(x)p_{2}(x) \cdots p_{r}(x) \]

dove \(p_{i}\) sono polinomi monici irriducibili, \(k\) è un numero razionale. La fattorizzazione è unica, a parte l’ordine dei fattori.

Dimostrazione
L’esistenza della fattorizzazione è ovvia. La costante \(k\) può essere calcolata in modo da rendere tutti i fattori dei polinomi monici.
Per dimostrare l’unicità supponiamo che esista un’altra fattorizzazione \(f(x) = k q_{1}(x)q_{2}(x) \cdots q_{s}(x)\). Per il teorema precedente deve essere \(p_{1}(x)|q_{i}(x)\) per qualche indice \(i\). Per comodità possiamo riordinare i polinomi della seconda fattorizzazione in modo che \(p_{1}(x)=q_{1}(x)\). Poiché sono entrambi polinomi monici irriducibili deve essere \(p_{1}(x)=q_{1}(x)\). Eliminando questi fattori e proseguendo il ragionamento, arriviamo alla conclusione che

\[ r=s \ ,\quad p_{1}(x)=q_{1}(x) \ ,\quad p_{2}(x)=q_{2}(x) \ ,\quad \cdots \ ,\quad p_{r}(x)=q_{r}(x) \]

Criterio di Eisenstein
Diamo ora un criterio utile per determinare se un polinomio è irriducibile. Sia

\[ f(x)= a_{0}+ a_{1}x+ \cdots + a_{n}x^{n} \]

un polinomio a coefficienti interi. Supponiamo che esista un primo \(q\) tale che:

• \( q\) non divide \(a_{n} \)
• \( q\) divide \(a_{0},a_{1},\cdots,a_{n-1}\)
• \(q^{2}\) non divide \( a_{0}\)

Allora \(f(x)\) è irriducibile sui razionali.

Dimostrazione
Per il teorema di Gauss è sufficiente dimostrare che \(f(x)\) è irriducibile sugli interi. Supponiamo per assurdo che \(f=gh\):

\[ \begin{array}{l} g(x)= b_{0}+ b_{1}x+ \cdots + b_{r}x^{r} \\ h(x)= c_{0}+ c_{1}x+ \cdots + c_{s}x^{s} \\ \end{array} \]

Allora \(r+s=n\). Ora \(a_{0}=b_{0}c_{0}\) e quindi \(q|b_{0}\) oppure \(q|c_{0}\). Tuttavia non può dividerli entrambi e quindi possiamo supporre, senza perdita di generalità, che \(q|b_{0}\) ma non divide \( c_{0}\). Se tutti i coefficienti \(b_{i}\) fossero divisibili per \(q\), allora \(a_{n}\) sarebbe divisibile per \(q\), ma questo non è possibile per le ipotesi. Sia quindi \(b_{i}\) il primo coefficiente di \(g(x)\) non divisibile per \(q\). Allora

\[ a_{i}=b_{i}c_{0}+ \cdots + b_{0}c_{i} \]

dove \(i \lt n\). Questo implica che \(q|c_{0}\) in quanto divide \(a_{i},b_{0},b_{1},\cdots,b_{i-1}\), ma non divide \(b_{i}\). Abbiamo una contraddizione e quindi l’ipotesi che \(f(x)\) è riducibile non è vera.

Esempio 3.4
Dimostrare che il polinomio

\[ f(x)=x^{p-1}+ x^{p-2}+ \cdots + x + 1 \]

è irriducibile sul campo dei razionali \(\mathbb{Q}\).

Suggerimento
Espandere \(f(x+1)=(x+1)^{p-1}+ (x+1)^{p-2}+ \cdots + (x+1) + 1 \) ed esaminare i coefficienti. Se \(f(x+1)\) è irriducibile su \(\mathbb{Q}\) lo è anche \(f(x)\).

4) Campi finiti

Un campo finito è un campo con ordine finito, cioè con un numero finito di elementi. La teoria dei campi finiti ha trovato applicazione in importanti branche della matematica pura e applicata, come algebra, analisi combinatoria, teoria dei codici, crittografia, ecc.

Esempio 4.1
Il caso più semplice di campo finito è il campo \(GF(2)=F_{2}=\mathbb{Z}/2\mathbb{Z}=\{0,1\}\) costituito da due elementi. Le operazioni sul campo sono quelle binarie dell’operatore \(OR\) esclusivo (\(XOR\)), che indichiamo con \(+\):

\[ \begin{array}{l} 0+0 = 0 \ ,\quad 0+1=1 \ ,\quad 1+0=1 \ ,\quad 1+1 = 0 \\ 0 \cdot 0 =0 \ ,\quad 0 \cdot 1=0 \ ,\quad 1 \cdot 0=0 \ ,\quad 1 \cdot 1 =1 \end{array} \]

In generale l’anello \(\mathbb{Z}/\mathbb{nZ}\), con \(n \gt 2\), non è un campo (vedi anche esercizio 2.8).

Esercizio 4.1 – Il campo \(GF(4)\)
Consideriamo il seguente insieme: \(F=\{0,1,a,b\}\). Definiamo le operazioni di addizione e moltiplicazione, definite mediante le seguenti tabelle:

\[ \begin{array}{r|rrrr} + \quad & 0\ &\ 1\ &\ a\ &\ b \\ \hline 0\quad &\ 0\ &\ 1\ &\ a\ &\ b\ \\ 1\quad &\ 1\ &\ 0\ &\ b\ &\ a\ \\ a\quad &\ a \ &\ b\ &\ 0\ &\ 1\ \\ b\quad &\ b\ &\ a\ &\ 1\ &\ 0\ \end{array} \quad \quad \begin{array}{r|rrrr} \times \quad & 0\ &\ 1\ &\ a\ &\ b \\ \hline 0\quad &\ 0\ &\ 0\ &\ 0\ &\ 0\ \\ 1\quad &\ 0\ &\ 1\ &\ a\ &\ b\ \\ a\quad &\ 0 \ &\ a\ &\ b\ &\ 1\ \\ b\quad &\ 0\ &\ b\ &\ 1\ &\ a\ \end{array} \]

Dimostrare che si tratta di un campo finito di ordine \(4\), che possiamo indicare con \(GF(4)\) oppure con \(F_{4}\).

Definizione 4.1
La caratteristica di un campo è il più piccolo intero positivo \(n\) tale che

\[ \underbrace{1+1+ \cdots +1 }_{n \text{ volte}}=0 \]

Se tale intero positivo non esiste si dice che il campo ha caratteristica uguale a 0.
I campi \(\mathbb{Q},\mathbb{R}\) hanno caratteristica uguale a \(0\).

Teorema 4.1
La caratteristica di un campo \(F\) è uguale a \(0\) oppure è un numero finito. Nel caso finito, la caratteristica è un numero primo.

Dimostrazione
Supponiamo che la caratteristica sia un numero intero positivo composto, cioè \(\text{char}(F)=ab, a,b \neq 1\). Per ipotesi

\[ \begin{array}{l} \underbrace{1+1+ \cdots +1}_{a \text{ volte}} \neq 0 \\ \underbrace{1+1+ \cdots +1}_{b \text{ volte}} \neq 0 \\ \end{array} \]

Moltiplicando le due sequenze abbiamo

\[ \begin{array}{l} (\underbrace{1+1+ \cdots +1}_{a \text{ volte}})( \underbrace{1+1+ \cdots +1}_{b \text{ volte}})= \underbrace{1+1+ \cdots +1}_{ab \text{ volte}}=0 \end{array} \]

Questa è una contraddizione in quanto il gruppo abeliano moltiplicativo \(F^{*}\) per definizione non contiene l’elemento \(0\), ma il prodotto \(ab\) deve appartenere a \(F^{*}\).

Esercizio 4.2 
Dimostrare che se \(p\) è un numero primo e \(F\) è un campo con caratteristica uguale a \(p\), allora:

\[ (a+b)^{p}=a^{p}+ b^{p} \quad \forall a,b \in F \]

Suggerimento
Utilizzare il teorema binomiale e ricordare che \( \displaystyle p|\binom{p}{k}\) con \(1 \le k \lt p\).

Teorema 4.1 – Il campo \(\mathbb{Z}_{p}=GF(p)\)
Sia \(p\) un numero primo. Allora l’anello \(\mathbb{Z}_{p}\) è un campo di ordine \(p\).

Dimostrazione
Chiaramente \(\mathbb{Z}_{p}\) è un anello commutativo con unità. Si deve solo dimostrare che ogni elemento non nullo ha un inverso moltiplicativo. Ma, per il teorema di Fermat, ogni numero \(a\) primo con \(p\) ha un inverso. Infatti

\[ a \in \mathbb{Z}_{p}-\{0\} \implies (a,p)=1 \implies \exists x: ax \equiv 1 \pmod {p} \]

Definizione 4.2
Il più piccolo sottocampo di un campo \(F\) si chiama sottocampo primo. Può essere definito anche come l’intersezione di tutti i sottocampi di \(F\).
Sia \(S\) un sottoinsieme di un campo \(F\). Si chiama sottocampo di \(F\) generato da \(S\) l’intersezione di tutti i sottocampi che contengono l’insieme \(S\).

Si può dimostrare il seguente teorema:

Teorema 4.2
Il sottocampo primo \(K\) di un campo finito \(F\) è il sottocampo generato da \(1\).

Dimostrazione
Sia \(p=\text{char}(F)\). Allora il sottocampo \(K\) generato da \(1\) contiene \(p\) elementi. Sia \(K=\{0,1,\cdots, p-1\}\). Poiché ogni sottocampo di \(F\) deve contenere il sottogruppo additivo generato da \(1\), ne deriva che \(K\) è il sottocampo primo di \(F\).

Vale il seguente fondamentale teorema:

Teorema 4.3
Supponiamo che \(F\) sia un campo finito e sia \(K\) un sottocampo di \(F\) contenente \(q\) elementi. Allora \(F\) è uno spazio vettoriale su \(K\) e \(|F|=q^{m}\), dove \(m\) è la dimensione dello spazio vettoriale \(F\) su \(K\).

Dimostrazione
È facile verificare che \(F\) è uno spazio vettoriale su \(K\). Poiché \(F\) è finito, esiste una base finita dello spazio vettoriale \(B=\{b_{1}, \cdots,b_{m}\}\). Ogni elemento \(a\) di \(F\) può essere espresso in modo univoco come combinazione lineare degli elementi della base: \(a=a_{1}b_{1}+ \cdots +a_{m}b_{m} \), dove \(a_{i} \in K\). In totale gli elementi di \(F\) sono le \(m\)-uple di elementi di \(K\) cioè \(q^{m}\).
Il valore di \(m\) viene chiamato grado di \(F\) su \(K\).
Dal teorema precedente, ricordando che ogni campo finito ha come caratteristica un numero primo, deriva il seguente:

Teorema 4.4
Sia \(F\) un campo finito con \(q\) elementi. Allora \(q=p^{n}\), dove \(p\) è la caratteristica di \(F\) e \(n\) è il grado di \(F\) sul suo sottocampo primo.

Abbiamo quindi dimostrato che ogni campo finito ha come ordine la potenza di un numero primo. Si può dimostrare anche il seguente teorema di esistenza:

Teorema 4.5
Per ogni numero primo \(p\) e ogni numero intero positivo \(m \ge 1\) esiste un campo con \(p^{m}\) elementi.
Si può anche dimostrare che tutti i campi finiti di un certo ordine \(q=p^{n}\) sono isomorfi fra loro, cioè sono equivalenti dal punto di vista algebrico.

4.1) Generatori di un campo finito

Consideriamo ora l’insieme \(F_{q}^{*}\) degli elementi non nulli di un campo finito. Si tratta di un gruppo abeliano con l’operazione di moltiplicazione. Si chiama ordine di un elemento \(a\) di \(F_{q}^{*}\) il più piccolo intero positivo \(d\) tale che \(a^{d}=1\).

Esercizio 4.3
Sia \(F\) un campo finito con \(q\) elementi, e sia \(a \in F\) con \(a \neq 0\). Allora

\[ a^{q-1}=1 \]

Segue anche che \(a^{q}=a\) per ogni \(a \in F\).

Suggerimento
Utilizzare il teorema di Lagrange.

Nel caso del campo \(\mathbb{Z}_{p}\) ritroviamo il teorema di Fermat.
Dal teorema precedente segue facilmente il seguente:

Teorema 4.6
L’ordine di ogni \(a \in F_{q}^{*}\) divide \(q-1\).

Definizione 4.3 – Generatori di un campo finito
Un generatore di un campo finito \(F_{q}\) è un elemento non nullo \(g \in F_{q}\) tale che ogni elemento del campo è uguale ad una potenza di \(g\). In altri termini un generatore è un elemento di ordine \(q-1\).
Un generatore si chiama anche elemento primitivo di \(F_{q}\).

Teorema 4.7
Ogni campo finito ha un generatore. Inoltre se \(g\) è un generatore allora è un generatore anche \(g^{i}\), dove \((i,q-1)=1\).

Dal teorema precedente segue che il numero dei generatori distinti di \(F_{q}^{*}\) è uguale a \(\varphi(q-1)\) dove \(\varphi(n)\) è la funzione di Eulero, che conta il numero degli interi \(1\le k \le n\) che sono primi con \(n\).
Il risultato fondamentale è quindi che il gruppo moltiplicativo \( F_{q}^{*}\) di un campo finito \(F_{q}\) è un gruppo ciclico.

Esempio 4.2
ll gruppo moltiplicativo del campo \(\mathbb{Z}_{p}\) indicato con \(\mathbb{Z}_{p}^{*}\) contiene gli elementi \(1,2,\cdots,p-1\). Quindi il gruppo moltiplicativo \(Z_{p}^{*}\) è un gruppo ciclico.

Esercizio 4.4 – Il gruppo \(\mathbb{Z}_{13}^{*}\)
In questo caso abbiamo

\[ \begin{array}{l} \mathbb{Z}_{13}=\{0,1,2,3,\cdots,12\} \\ \mathbb{Z}_{13}^{*}=\{1,2,3,\cdots,12\} \\ \end{array} \]

Il numero dei generatori è uguale a \(\varphi(12)=4\). Determinare i quattro generatori.

Soluzione: [\(2,6,7,11\)]

5) Polinomi sui campi finiti

Studiamo ora alcune proprietà specifiche dei campi finiti \(F_{q}=GF(p^{n})\), con \(q=p^{n}\), e dell’anello dei polinomi \(F_{q}[x]\).
Ricordiamo che un polinomio \(f(x) \in F_{q}[x]\) si dice irriducibile se non può essere fattorizzato nel prodotto di due polinomi \(h(x),g(x) \in F_{q}[x]\) di grado inferiore.

Esempio 5.1
Il polinomio \(f(x)=x^{5} + x^{4}+ 1\) è riducibile in \(GF(2)[x]\), in quanto

\[ x^{5} + x^{4}+ 1= (x^{2}+ x+1)(x^{3}+x+ 1) \]

È facile verificare che il polinomio \(f(x)=x^{2} + x+ 1\) è irriducibile in \(GF(2)[x]\), cioè non esistono due elementi \(a,b \in \{0,1\}\) tali che \(f(x)=(x-a)(x-b)\).
Si può dimostrare che ogni polinomio irriducibile di grado \(n\) nell’anello \(F_{q}[x]\) divide il polinomio \(x^{q^{n}-1}-1\). In base a questo risultato possiamo dare una definizione equivalente di polinomio primitivo:

Definizione 5.1
Un polinomio irriducibile \(f(x) \in F_{q}[x]\) di grado \(n\) si dice primitivo se il più piccolo intero positivo \(m\) per il quale \(f(x)\) divide \(x^{m}-1\) è \(m=q^{n}-1\).

Esempio 5.2
Il polinomio \(x^{4}+x^{3}+x^{2}+x +1 \) è irriducibile in \(F_{2}[x]\). Tuttavia non è primitivo in quanto è un fattore di \(x^{5}-1\).

Osserviamo che in \(F_{2}[x]\) abbiamo \(x^{5}-1=x^{5}+1\).

Esempio 5.3
Il polinomio \(x^{3}+x +1 \) è irriducibile in \(F_{2}[x]\). È anche primitivo in quanto non divide nessuno dei polinomi \(x^{4}-1\), \(x^{5}-1\), \(x^{6}-1\).

Esempio 5.4
In \(F_{2}[x]\) abbiamo

\[ (1+x+ x^{2})^{4}=(1+x^{2}+x^{4})^{2}=1+x^{4}+x^{8} \]

Esercizio 5.1
Dimostrare che il polinomio \(f(x)= x^{4}+x+1 \in F_{2}[x]\) è irriducibile su \(F_{2}\).
Dimostrare che è anche un polinomio primitivo.

5.1) Costruzione dei campi finiti

L’esempio base di campo finito è costituito dal campo \(F_{p}=GF(p)=\mathbb{Z}/p\mathbb{Z}\), dove \(p\) è un numero primo. ll processo di costruzione dei campi finiti che estendono il campo \(F_{p}\) è simile a quello usato nel caso reale, utilizzato per costruire dei campi infiniti a parte dal campo base \(\mathbb{Q}\) dei numeri razionali. Ad esempio il campo \(\mathbb{Q}(\sqrt{2})\) viene costruito prendendo il polinomio \(f(x)=x^{2}-2\) che non ha radici razionali. Si prende una delle due radici reali, ad esempio \(\alpha=\sqrt{2}\) e si considera l’insieme

\[ \mathbb{Q}(\sqrt{2})= \{x+\alpha y, \ x,y, \in \mathbb{Q}\} \]

Questo insieme con le normali operazioni di addizione e moltiplicazione è un campo infinito.
Per costruire un campo finito \(F_{q}=GF(p^{m})\), dove \(q=p^{m}\), possiamo utilizzare un polinomio primitivo \(f(x)\) su \(F_{p}\) di grado \(m\).
I passi per costruire un campo finito di ordine \(p^{m}\), con \(p\) primo e \(m\) intero positivo maggiore di \(1\), sono i seguenti.

• Prendere un polinomio primitivo \(f(x)\) di grado \(m\) appartenente all’anello \(F_{p}[x]=GF(p)[x]\).
• Le operazioni di somma e prodotto modulo \(f(x)\) sono le stesse dell’anello \(F_{p}[x]\), ma ridotte modulo \(f(x)\).
• Indichiamo con \(\alpha\) una radice di \(f(x)\), cioè \(f(\alpha)=0\). Il campo finito \(F_{q}=GF(p^{m})\) contiene i seguenti elementi: \(\{0,1=\alpha^{0},\alpha^{1}, \cdots, \alpha^{p^{m}-2}\}\). Gli elementi vanno presi modulo \(f(\alpha)\).

Il campo finito \(GF(p^{m})\) può essere rappresentato nei tre seguenti modi equivalenti:

\[ \begin{array}{l} \displaystyle F_{q}= F_{p}[x]/(f(x))=\{a_{0} +a_{1}x + \cdots +a_{m-1}x^{m-1}\} \ ,\quad a_{i} \in F_{p},i=0,1,\cdots,m-1 \\ F_{q}=\{0,1=\alpha^{0},\alpha^{1}, \cdots, \alpha^{p^{m}-2}\} \\ F_{q}=\{a_{0},a_{1}, \cdots,a_{m-1}\} \ ,\quad a_{i} \in F_{p},i=0,1,\cdots,m-1 \end{array} \]

Esempio 5.5
Costruiamo il campo \(GF(2^{2})\) a partire dal polinomio \(f(x)=x^{2}+x+1 \in GF(2)[x]\). Indichiamo con \(\alpha\) una radice del polinomio \(f(x)\). In questo caso \(\alpha^{2}=1+\alpha\). Quindi gli elementi del campo \(GF(4)\) sono i seguenti: \(\{0,1,\alpha, 1+\alpha\}\). Le tabelle per le due operazioni sono le seguenti:

\[ \begin{array}{r|rrrr} + & 0 & 1 & \alpha & \alpha +1 \\ \hline 0 & 0 & 1 &\alpha & \alpha +1 \\ 1 & 1 & 0 & \alpha +1 & \alpha \\ \alpha & \alpha & \alpha +1 & 0 & 1 \\ \alpha +1 & \alpha +1 & \alpha & 1 & 0\ \end{array} \] \[ \begin{array}{r|rrrr} \times & 0 & 1 & \alpha & \alpha +1 \\ \hline 0 & 0\ & 0 & 0 & 0 \\ 1 & 0 & 1 &\alpha & \alpha +1 \\ \alpha & 0 & \alpha & \alpha +1 & 1 \\ \alpha +1 & 0 & \alpha +1 & 1 & \alpha \end{array} \]

Esempio 5.6
Costruiamo il campo \(GF(2^{3})\) a partire dal polinomio \(f(x)=x^{3}+x^{2}+1 \in GF(2)[x]\).

Ogni elemento di \(GF(2^{3})\) può essere rappresentato da una tripletta di coefficienti binari: \((a_{0},a_{1},a_{2})\).
Ricordiamo che se \(\alpha\) è uno zero di \(f(x)\) allora

\[ f(\alpha)=\alpha^{3}+ \alpha^{2}+1 = 0 \implies \alpha^{3}=-\alpha^{2}-1=\alpha^{2}+1 \]

Dimostrare che la lista degli elementi di \(GF(2^{3})\) è la seguente:

\[ \begin{array}{|c|c|c|} \hline \alpha^{k} & \text{polinomio} \ &\text{binario} \\ \hline 0 & 0 & 000 \\ \hline \alpha^{0} & 1 & 100 \\ \hline \alpha^{1} & \alpha & 010 \\ \hline \alpha^{2} & \alpha^{2} & 001 \\ \hline \alpha^{3} & \alpha^{2}+1 & 101 \\ \hline \alpha^{4} & \alpha^{2}+\alpha +1 & 111 \\ \hline \alpha^{5} & \alpha +1 & 110 \\ \hline \alpha^{6} & \alpha^{2}+\alpha & 011 \\ \hline \end{array} \]

Per un approfondimento della teoria dei numeri applicata alla crittografia vedere il testo eccellente di Koblitz ^[4].

6) I cifrari a flusso

Un cifrario a flusso è un sistema crittografico simmetrico nel quale i simboli del messaggio (bit o byte) sono cifrati indipendentemente l’uno dall’altro. In pratica viene utilizzato un generatore di numeri pseudo-casuali, che utilizza una chiave segreta, condivisa fra il mittente e il destinatario. A partire dal messaggio e dalla chiave viene creata una stringa casuale di caratteri, della stessa lunghezza del messaggio. Il testo cifrato viene ottenuto effettuando una operazione logica di XOR (OR esclusivo) fra la stringa pseudo-casuale e il messaggio in chiaro. La decifratura avviene con la stessa modalità effettuando l’operazione logica di XOR tra il testo cifrato e la chiave segreta.
Prima di descrivere il funzionamento dei cifrari a flusso ricordiamo alcuni concetti sugli algoritmi di generazione di numeri casuali.

6.1) I generatori di numeri casuali

Il concetto di numero casuale è collegato alle proprietà di una successione di numeri. Teoricamente i numeri della sequenza non dovrebbero avere alcuna correlazione tra loro. Una caratteristica fondamentale di una sequenza di numeri casuali è che deve avere la proprietà dell’uniformità. Per una definizione precisa è necessario ricordare le proprietà della distribuzione uniforme, che è la più semplice tra le distribuzioni di probabilità.
Per una variabile aleatoria discreta uniforme \(X\), che può assumere un numero finito di valori \(\{x_{1},x_{2}, \cdots, x_{n}\}\), ogni valore deve avere la stessa probabilità:

\[ P(X=x_{i})= \frac{1}{n} \ ,\quad i=1,2,\cdots,n \]

Una sequenza di numeri casuali può essere ottenuta effettuando \(n\) lanci di un dado. In questo caso la variabile aleatoria può assumere i valori \(X=\{1,2,3,4,5,6\}\), ognuno con probabilità \(p=\dfrac{1}{6}\).

Un generatore di numeri casuali, identificato con la sigla RNG (random number generator) può essere un dispositivo fisico o meccanico, oppure un algoritmo matematico. Naturalmente per verificare la bontà del processo di generazione è necessario analizzare una quantità grande di numeri e sottoporre il processo ad opportuni test statistici. Esistono due categorie principali di generatori di numeri casuali:

• Pseudo Random Number Generators (PRNG), chiamati anche Deterministic Random Number Generators (DRNG)
• True Random Number Generators (TRNG)

I generatori TRNG generano numeri casuali a partire da fenomeni fisici di varia natura (ad esempio il rumore di fondo nell’atmosfera, il decadimento radioattivo, ecc.). La procedura consiste nel riuscire a registrare le più piccole variazioni delle grandezze fisiche associate al fenomeno fisico.
Un generatore di numeri pseudo-casuali (PRNG) è costituito da un algoritmo deterministico che genera una sequenza di numeri. La sequenza deve naturalmente approssimare alcune proprietà caratteristiche dei numeri casuali. L’algoritmo prevede un input iniziale, chiamato il seme (seed) del PRNG. Ogni sequenza di numeri è completamente determinata dal seme iniziale: se si utilizza lo stesso seme iniziale la sequenza generata è sempre la stessa. La scelta del seme iniziale è molto importante; una gestione non corretta potrebbe rendere un sistema vulnerabile ad attacchi informatici. La scelta ottimale del seme deve permettere di generare una sequenza diversa ogni volta che si esegue l’algoritmo.
Esistono diversi esempi di PRNG. I più utilizzati per la crittografia sono i registri a scorrimento con retroazione lineare e i registri non lineari.
Per maggiori informazioni sui generatori di numeri casuali vedere articolo, oppure il testo di Knuth ^[3].

6.2) Il cifrario di Vernam (One Time Pad)

Prima di introdurre i cifrari a flusso, descriviamo brevemente il cifrario One Time Pad, conosciuto anche come cifrario di Vernam, inventato nel \(1917\) da Gilbert Vernam (1890-1960).
Supponiamo utilizzare l’alfabeto inglese di \(26\) lettere e di trasmettere testi di lunghezza fissata \(n\). L’insieme delle chiavi è costituito dalle \(26^{n}\) stringhe di \(n\) lettere; la distribuzione delle stringhe è uniforme, cioè ogni stringa ha la stessa probabilità \(p=\dfrac{1}{26^{n}}\).
Scegliamo in modo casuale una chiave \(k=k_{1}k_{2}\cdots k_{n}\) e supponiamo di trasmettere un testo testo in chiaro \(m=m_{1}m_{2}\cdots m_{n}\). Il testo cifrato \(c\) è il seguente:

\[ c=c_{1}c_2{\cdots c_{n}} \quad \text{dove } c_{i}=m_{i}\oplus k_{i} \]

Esempio 6.1
Nel codice Ascii la lettera “A” è codificata con la stringa binaria “01000001”. Supponendo la chiave uguale a “11001010” la cifratura con l’algoritmo One Time Pad è la seguente:

\[ \begin{array}{|c|c|c|c|c|l|} \hline m \quad & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & \text{messaggio in chiaro} \\ \hline k \quad & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & \text{chiave} \\ \hline c= m \oplus k \quad & 1 &0 & 0 & 0 & 1 & 0 & 1 & 1 & \text{messaggio cifrato}\\ \hline \end{array} \]

Nel 1949 Claude Shannon, considerato il padre della teoria dell’informazione, pubblicò il suo lavoro fondamentale ‘Communication Theory of Secrecy Systems‘. In particolare Shannon introdusse il concetto di segretezza perfetta: un crittosistema è a segretezza perfetta se

\[ P(m|c) = P(m) \quad \forall m \in M \text{ e } \forall c \in C \]

cioè se la probabilità a posteriori che il testo in chiaro sia \(m\), dato che il testo cifrato è \(c\), è uguale alla probabilità a priori che il testo in chiaro sia \(m\).
Shannon dimostrò che il cifrario di Vernam costituisce un sistema perfetto di segretezza. Tuttavia questo sistema è poco pratico, in quanto richiede una chiave di lunghezza uguale a quella del testo in chiaro. Dal punto di vista pratico è preferibile utilizzare una chiave più corta, anche se questo comporta un livello minore di sicurezza.
Comunque il cifrario di Vernam può essere utile nel caso di applicazioni specifiche e critiche.

6.3) Struttura dei cifrari a flusso

I cifrari a flusso cercano di approssimare l’algoritmo One Time Pad, rinunciando ad utilizzare una chiave lunga quanto il messaggio da trasmettere. In particolare si rinuncia alla completa casualità della chiave, quindi si abbassa il livello di sicurezza.
Per creare le chiavi si utilizzano gli algoritmi PRNG, che come abbiamo visto sono in grado di generare numeri pseudo-casuali. Nonostante la chiave non sia sicura al 100%, tuttavia per molte applicazioni questo sistema è pratico e sufficientemente sicuro.
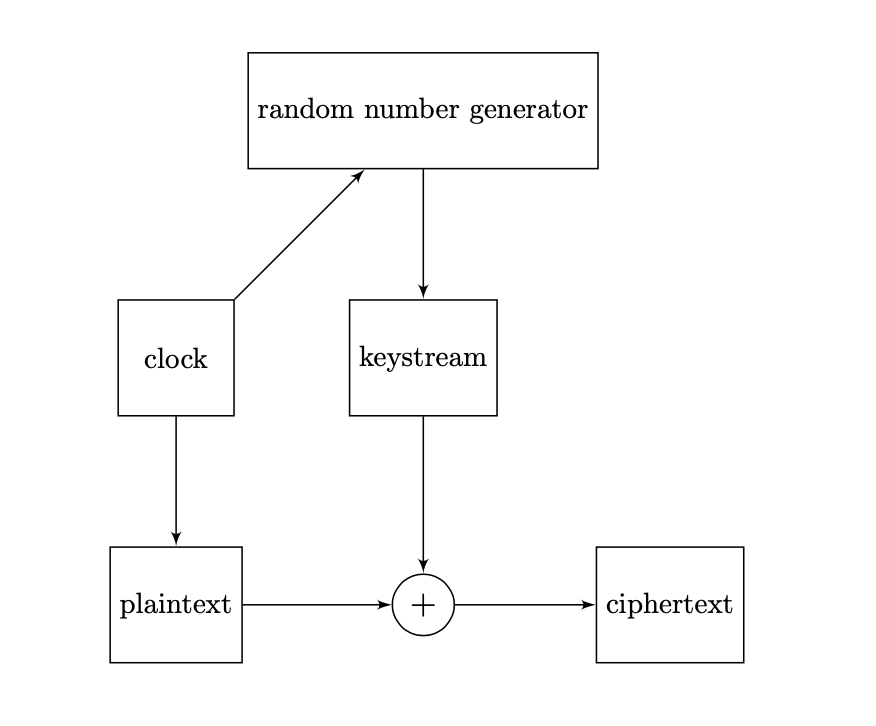
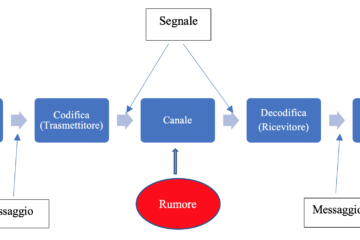
Come abbiamo visto in precedenza, un algoritmo PRNG è una funzione deterministica che produce una stringa in output di lunghezza maggiore della stringa in input. Possiamo immaginarlo come una funzione che ha in input un seme iniziale e una lunghezza \(L\), e in output crea una stringa pseudo-casuale di lunghezza \(L\). Il seguente diagramma illustra il processo di cifratura di un testo in chiaro:

L’operazione di decifratura si ottiene invertendo i ruoli del testo in chiaro e del testo cifrato.
Il termine keystream indica un flusso di caratteri pseudo-casuali che sono combinati con il messaggio in chiaro per produrre il messaggio cifrato. Il keystream viene prodotto dal generatore di numeri pseudo-casuali.
Ad ogni impulso dell’orologio, viene generato un bit (o un byte) dal generatore e viene effettuata l’operazione logica di XOR tra il keystream e il testo in chiaro, producendo il testo cifrato.

I cifrari a flusso vengono suddivisi in due categorie principali: cifrari sincroni e cifrari auto-sincronizzanti. Un cifrario a flusso si dice sincrono se il keystream è costruito a partire dalla chiave in modo indipendente dal testo in chiaro che si deve cifrare. Per poter funzionare sia il mittente che il destinatario devono essere sincronizzati, cioè devono utilizzare la stessa chiave e lavorare nello stesso stato data la chiave. Un cifrario a flusso si dice auto-sincrono se ogni elemento del keystream dipende dal precedente testo in chiaro: la sequenza cifrata è ottenuta dalla combinazione del keystream, del testo in chiaro e dei caratteri in precedenza cifrati.

6.4) Confusione e diffusione

Un cifrario sicuro dovrebbe nascondere le proprietà statistiche del testo in chiaro, per rendere difficili le operazioni di attacco al codice. Shannon introdusse due concetti importanti per caratterizzare gli algoritmi crittografici: confusione e diffusione. Entrambi questi concetti sono utilizzati per impedire la possibilità di ricostruire la chiave, o in generale il testo in chiaro, a partire dal testo cifrato (vedi articolo su questo sito). 
La confusione riguarda la relazione fra il testo cifrato e la chiave simmetrica, che deve essere la più complessa possibile, in modo da rendere difficile scoprire la chiave.
La diffusione riguarda la relazione fra il testo in chiaro e il testo cifrato, che deve essere la più complessa possibile. In altre parole un singolo bit del testo in chiaro dovrebbe avere influenza su diversi bit del testo cifrato.
I cifrari a flusso garantiscono la confusione, ma non la diffusione, in quanto ogni bit del testo in chiaro è mappato su un singolo bit del testo cifrato.

7) Codici con registri a scorrimento con retroazione (feedback) lineare

Una modalità diffusa per creare i cifrari a flusso è quella che utilizza i registri a scorrimento con retroazione lineare (LFSR – linear feedback shift register). Un registro a scorrimento lineare di lunghezza \(n\) è composto da \(n\) elementi di memoria binaria, chiamati anche stadi, che possono contenere i valori \(0,1\). Il registro può trovarsi in \(2^{n}\) configurazioni diverse, in corrispondenza ad ognuna delle possibili n-uple di cifre binarie \(\{s_{0},s_{1},\cdots,s_{n-1}\}\).
In generale abbiamo un insieme di celle collegate in serie, come illustrato nel seguente diagramma:

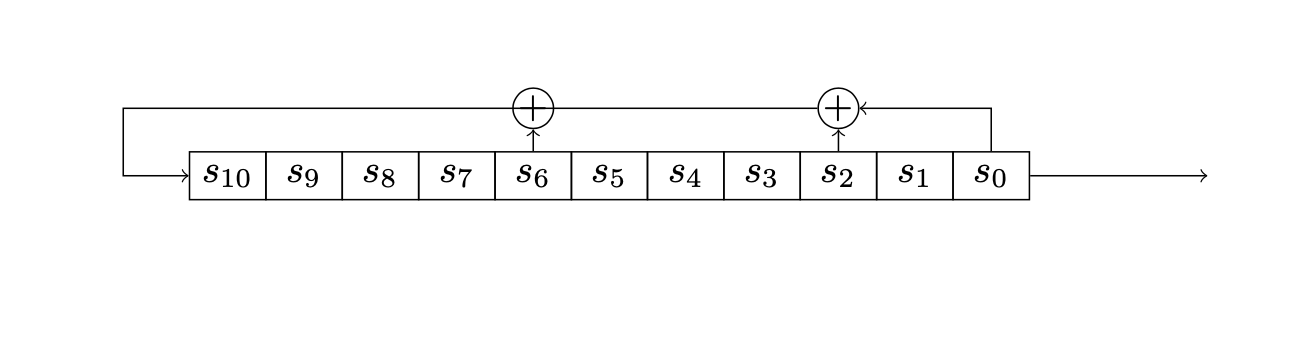
Ad intervalli di tempo regolari scanditi da un orologio, il contenuto di ciascuno stadio viene trasferito nello stadio di destra ed il contenuto di \(s_{0}\) “esce” dal registro. Anche il contenuto dello stadio più a sinistra, \(s_{n-1}\), va aggiornato: ciò viene effettuato mediante la funzione di retroazione, detta “feedback” del registro.
Il cambiamento di stato ad ogni ciclo è rappresentato dalla seguente trasformazione:

\[ \{s_{0},s_{1},\cdots,s_{n-1}\} \to \{s_{1},s_{2},\cdots,s_{n-2},f(s_{0},s_{1}, \cdots,s_{n-1})\} \]

Nel caso dei registri LFSR, la funzione di retroazione \(f\) è una funzione lineare di \(n\) variabili, che utilizza alcuni dei bit memorizzati nel registro per determinare il nuovo valore di \(s_{n-1}\). Nel caso più semplice è un addizionatore collegato ad alcuni stadi, che somma il contenuto di questi stadi prima che il registro venga aggiornato e imposta il valore calcolato nella cella \(s_{n-1}\).
Indichiamo con \(a_{0},a_{1},\cdots,a_{n-1}\) i coefficienti di retroazione associati ai vari stadi, i cui valori sono \(1\) oppure \(0\), a seconda che i rispettivi stadi siano collegati o non collegati all’addizionatore.
Il valore calcolato per lo stadio \(s_{n-1}\) al tempo \(t+1\) è quindi dato dalla seguente equazione lineare:

\[ s_{n-1}(t+1)=a_{0}s_{0}(t) + a_{1}s_{1}(t) + \cdots + a_{n-1}s_{n-1}(t) \quad \label{F7.1}\tag{7.1}\]

La chiave è data dallo stato iniziale e dai coefficienti di retroazione. Le uscite del registro sono costituite dalle cifre binarie pseudocasuali che via via occupano lo stadio \(s_{0}\).
I registri sono controllati da un orologio (clock) e ad intervalli prestabiliti il contenuto di una cella passa nella successiva.
Naturalmente escludiamo lo stato iniziale nullo, corrispondente alla n-upla \((0,0, \cdots,0)\), poiché in tal caso il registro emetterebbe soltanto degli zeri.
Se la relazione non è lineare allora si parla di registri a scorrimento non-lineari. Ad esempio possono essere introdotte operazioni di moltiplicazione.
Ad un registro a scorrimento di lunghezza \(n\) con coefficienti di retroazione \(a_{0},a_{1}, \cdots, a_{n-1}\) possiamo associare il polinomio monico di grado \(n\):

\[ f(x)= a_{0}+ a_{1}x^{1}+ \cdots + a_{n-1}x^{n-1}+ x^{n} \]

dove \(x\) può assumere i valori binari \(0,1\) e tutte le operazioni vengono fatte con l’aritmetica modulare di modulo 2.

7.1 ) Registri a periodo massimo

Una successione \(\{s_{0},s_{1},s_{2},\cdots \}\) si dice periodica se esiste un intero positivo \(d \gt 1\) tale che risulta \(s_{i}=s_{i+d}\) per tutti gli \(i \ge 0\). Si chiama periodo della sequenza il più piccolo intero \(d\) per il quale vale la proprietà.
Se la relazione \(s_{i}=s_{i+d}\) vale solo per valori di \(i\) sufficientemente grandi, allora la successione si dice eventualmente periodica.

Esercizio 7.1
Dimostrare che la sequenza generata da un registro LFSR è eventualmente periodica. Dimostrare anche che per un registro di lunghezza \(n\) il periodo massimo è \(2^{n}-1\).

La sequenza di uscita del registro è la stringa dei bit meno significativi. La dimensione della sequenza di bit prima che venga ripetuta è chiamata periodo. Abbiamo visto che un componente essenziale dei cifrari a flusso è il generatore della stringa pseudo-casuale (keystream) di cifre binarie. Due proprietà importanti del keystream sono le seguenti:

• avere caratteristiche pseudo-casuali, in grado di superare test statistici di casualità;
• avere un periodo il più lungo possibile.

Supponiamo ora che il polinomio associato al registro LFSR sia

\[ f(x)= a_{0}+ a_{1}x^{1}+ \cdots + a_{n-1}x^{n-1}+ x^{n} \]

La scelta del polinomio è fondamentale per avere un periodo massimo. Infatti vale il seguente teorema:

Teorema 7.1
Un registro LFSR di lunghezza \(n\) produce una sequenza di periodo massimo, cioè \(2^{n}-1\), se e solo se il polinomio \(f(x) \in \mathbb{Z}_{2}[x]\) associato al registro è primitivo.

In generale, se \(f(x)\) è un polinomio irriducibile ma non primitivo, allora il periodo della sequenza è minore del massimo teorico. Per ogni lunghezza \(n\) esiste almeno un polinomio primitivo di grado \(n\). In base al teorema precedente, il periodo massimo di una sequenza pseudo-casuale cresce esponenzialmente con la lunghezza del registro. La tabella riportata di seguito contiene alcuni polinomi primitivi modulo 2, di diverso grado.

Tabella polinomi primitivi
La seguente tabella contiene alcuni esempi di polinomi primitivi.

\[ \begin{array}{l|llll} \text{grado} \quad & \text{polinomi}\\ \hline 2 \quad & 1+ x + x^{2} \\ \hline 3 \quad & 1+ x + x^{3} \\ & 1+x^{2}+x^{3} \\ \hline 4 \quad & 1+ x + x^{4} \\ & 1+x^{3}+x^{4} \\ \hline 5 \quad & 1+ x^{2} + x^{5} \\ & 1+x^{3}+x^{5} \\ & 1+x^{2}+x^{3}+x^{4}+x^{5} \\ & 1+x+x^{2}+x^{3}+x^{5} \\ & 1+x+x^{2}+x^{4}+x^{5} \\ & 1+x+x^{3}+x^{4}+x^{5} \\ \hline \end{array} \]

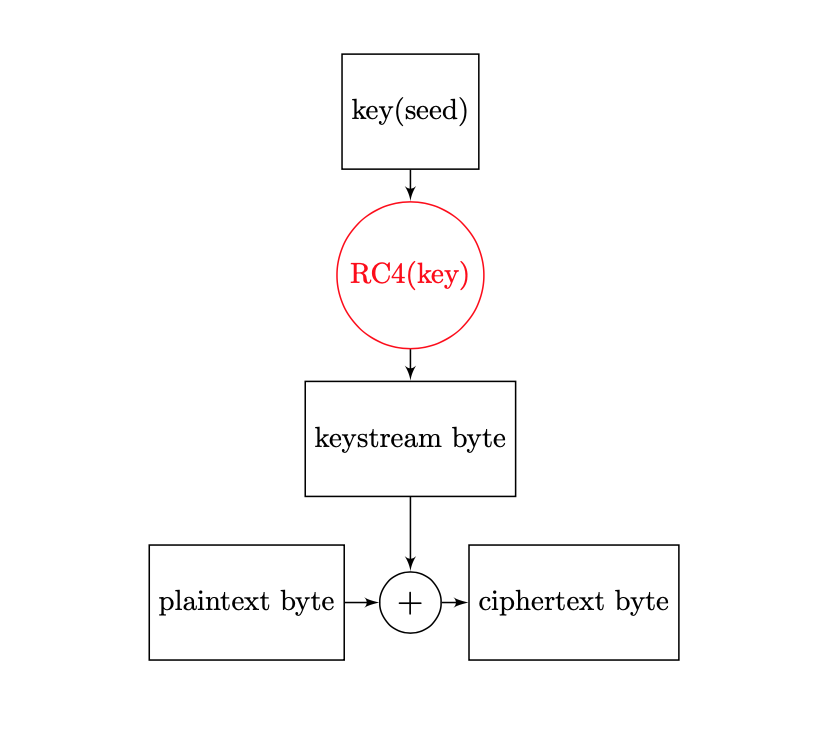
7.2) Il cifrario RC4

Uno dei cifrari a flusso più utilizzati è il cifrario RC4, progettato da Ron Rivest nel \(1987\). È utilizzato anche nei protocolli di trasmissione TLS (transport layer security) e SSL (secure socket layer). Come è noto TLS e SSL sono protocolli crittografia utilizzati per la trasmissione sicura dei dati sulle reti di computer, in particolare sulla rete internet.
Il cifrario RC4 crittografa i messaggi un byte per volta, invece che un bit. RC4 è un cifrario a flusso sincrono.

Le informazioni di stato sono contenute in un vettore \(S\), contenente le \(256\) stringhe binarie (bytes) corrispondenti ai numeri da \(0\) a \(255\). Il cifrario RC4 è costituito da due componenti:

• un algoritmo per la scelta della chiave (KSA)
• un algoritmo per la generazione dei numeri pseudo-casuali (PRGA)

Nella fase iniziale viene scelta una chiave \(K\) segreta mediante l’algoritmo KSA, utilizzata per inizializzare il vettore di stato \(S\). Quindi ad ogni ciclo, mediante l’algoritmo PRGA, viene generato un byte di keystream estraendo uno degli elementi del vettore \(S\).
Per la cifratura viene quindi seguita l’operazione di XOR fra il byte generato e il byte del messaggio in chiaro. Per la decifratura viene eseguita l’operazione di XOR fra il byte generato e il byte del messaggio cifrato.

8) Crittoanalisi dei cifrari a flusso con testo in chiaro

In generale per forzare un cifrario simmetrico è necessario conoscere la chiave utilizzata. Un modo per riuscire a scoprire la chiave utilizzata nei cifrari a flusso basati su registri lineari è quello di conoscere una coppia formata da un messaggio in chiaro e il corrispondente testo cifrato. Si tratta di una eventualità possibile in molte situazioni: basta avere accesso al sistema di cifratura e inserire un proprio messaggio, memorizzando il corrispondente cifrato.
Se la chiave iniziale (seed) del cifrario ha lunghezza \(n\), allora basta conoscere un messaggio di \(2n\) cifre e il corrispondente crittogramma per riuscire a forzare il cifrario. Ricordando il meccanismo di scorrimento del registro, possiamo scrivere le seguenti relazioni:

\[ \begin{array}{l} s_{1}(t)=s_{0}(t+1) \\ s_{2}(t)=s_{0}(t+2) \\ \vdots \\ s_{n-1}(t)=s_{0}(t+n-1) \\ \end{array} \]

In base alla formula \eqref{F7.1}, il contenuto dello stadio \(s_{0}\) ad un dato istante si può quindi esprimere come combinazione lineare dei valori di \(s_{0}\) negli \(n\) istanti precedenti:

\[ \begin{array}{l} s_{0}(t+n)=a_{0}s_{0}(t) + a_{1}s_{0}(t+1) + \cdots + a_{n-1}s_{0}(t+n-1) \quad \label{F8.1}\tag{8.1} \end{array} \]

Supponiamo ora di intercettare un messaggio \(m=m_{1}m_{2}\cdots m_{2n}\) in chiaro e il corrispondente messaggio cifrato \(c=c_{1}c_{2}\cdots c_{2n}\). Allora possiamo scrivere le seguenti equazioni:

\[ \begin{array}{l} c_{1} = m_{1} + s_{0}(1) \\ c_{2} = m_{2} + s_{0}(2) \\ \vdots \\ c_{2n} = m_{2n} + s_{0}(2n) \\ \end{array} \]

Risolvendo questo sistema troviamo i valori \(s_{0}(1),s_{2}(2), \cdots,s_{0}(2n)\).
Utilizzando la formula \eqref{F8.1} per gli \(n\) valori \(\{t=1,2,\cdots,n\}\) possiamo calcolare i coefficienti \(a_{0},a_{1},\cdots,a_{n-1}\).
A questo punto, sempre utilizzando la formula \eqref{F8.1}, possiamo calcolare i valori \(s_{2n+1}, s_{2n+2}, \cdots\) e quindi siamo in grado di forzare il cifrario.

Un modo per superare questo punto debole dei cifrari a flusso che utilizzano registri lineari è quello di utilizzare i registri a scorrimento non lineari, che hanno una funzione di feedback più complessa. Un altro modo è quello di combinare più registri a scorrimento lineari, per aumentare il grado di casualità delle sequenze.
Per un approfondimento dei cifrari a flusso vedere ^[5].

Conclusione

Il concetto base dei cifrari a flusso è di dividere un testo in piccole parti, un bit o un byte. I cifrari a flusso vengono usati in genere se la lunghezza dei messaggi in chiaro non è nota a priori, come nelle comunicazioni wireless e nella messaggistica istantanea.
In un prossimo articolo descriveremo i cifrari a blocchi, nei quali un testo viene diviso in blocchi abbastanza grandi, ad esempio di \(64\) o \(128\) bit, e ogni blocco viene crittografato separatamente. La maggior parte degli attuali sistemi di crittografia simmetrica è costituita da cifrari a blocco. I più famosi sono il DES (Data Encryption Standard) e l’AES (Advanced Encryption Standard).

Bibliografia

^[1]Birkhoff, Mac Lane – A Survey of Modern Algebra (A.K. Peters)

^[2]F. Ayres – Schaum’s Outline of Abstract Algebra (McGraw Hill)

^[3]D. Knuth – Art of Computer Programming, Volume 2: Seminumerical Algorithms (Addison Wesley)

^[4]N. Koblitz – A Course in Number Theory and Cryptography (Springer)

^[5]R. Rueppel – Analysis and Design of Stream Ciphers (Springer)