In questo articolo studieremo il secondo teorema di Shannon, relativo alla comunicazione su un canale in presenza di rumore. Nel \(1948\) Shannon dimostrò che è possibile trasmettere i dati con una data velocità e con una probabilità di errore piccola a piacere. Il massimo della velocità dipende dalla capacità del canale.
I risultati della Teoria dell’Informazione elaborata da Shannon si applicano a una grande varietà di situazioni: trasmissioni su linea telefonica, fibra ottica, comunicazioni wireless, trasmissioni via satellite. Possono essere estesi anche ad altri campi, come la biologia e la genetica molecolare.
1) Trasmissione su un canale rumoroso
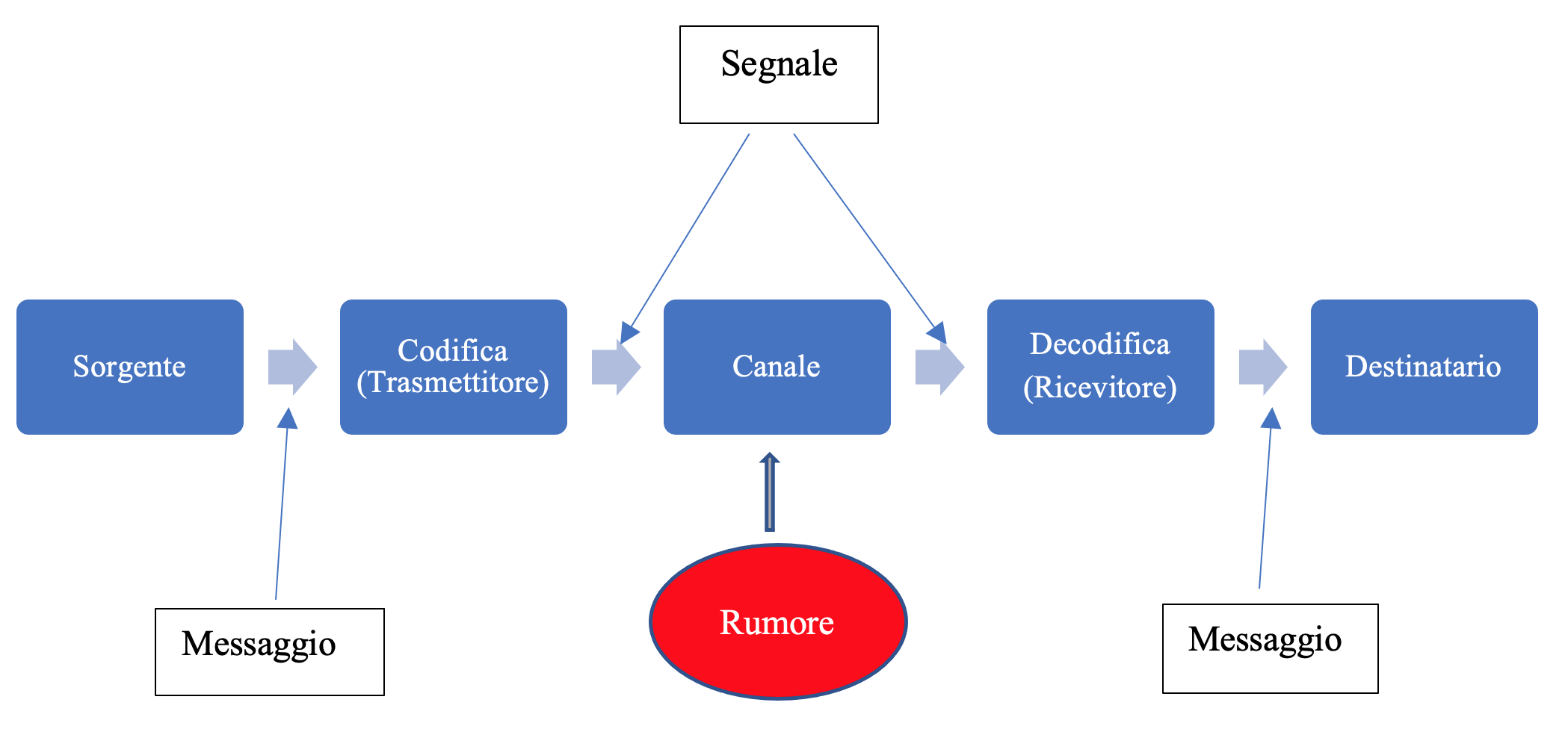
Il seguente diagramma illustra il paradigma di Shannon per la trasmissione su un canale:
Un canale di trasmissione discreto è costituito dai seguenti componenti:
- un alfabeto di input
- un alfabeto di output
- una matrice di probabilità condizionate
Sia \(A\) un alfabeto finito di simboli \(A=\{a_{1},a_{2},\cdots,a_{r}\}\), con una data distribuzione di probabilità
\[ p_{k}=P(a_{k}) \ , \quad k=1,2,\cdots,r \]I simboli dell’alfabeto \(A\) vengono dati in input al canale, attraverso il quale vengono trasmessi e raggiungono il punto finale di output.
A causa del rumore, i simboli che arrivano al punto di destinazione possono essere diversi e quindi appartenere ad un altro alfabeto \(B=\{b_{1},b_{2}, \cdots, b_{s}\}\) con distribuzione di probabilità
Ricordiamo che le proprietà di un canale sono determinate dalla sua matrice di transizione, i cui coefficienti sono le probabilità
\[ P_{ik}=P(b_{k}|a_{i}) \]Per semplicità prenderemo come modello il canale binario simmetrico (BSC). Si tratta di un canale discreto senza memoria, i cui alfabeti di input e output sono \(A=\{0,1\}\) e \(B=\{0,1\}\). Il funzionamento del canale dipende da un parametro di probabilità \(p_{e}\) compreso nell’intervallo \([0,1]\), che indica la probabilità di errore. Si dice simmetrico poiché la probabilità di ricevere \(1\) quando si è inviato \(0\) è la stessa di ricevere \(0\) quando si è inviato \(1\). La matrice di probabilità è la seguente:
\[ \begin{pmatrix} 1-p_{e} & p_{e} \\ p_{e} & 1-p_{e} \\ \end{pmatrix} \]Supponiamo che \(p_{e} \gt 0\), cioè che sia presente rumore nel canale. In presenza di rumore in genere l’output del canale, cioè il flusso dei simboli ricevuti, non è lo stesso di quello codificato in input al canale. Nei canali numerici binari l’errore di trasmissione può essere definito come il rapporto fra il numero dei bit errati rispetto al numero totale dei bit ricevuti. Gli errori possono essere dovuti sia a fattori esterni sia a limitazioni della banda di trasmissione del canale, in quanto il segnale può attenuarsi nella trasmissione e diventare non riconoscibile.
Per riconoscere ed eventualmente correggere gli errori di trasmissione, si sfrutta la ridondanza dei dati, nella fase di preparazione della codifica di canale. Maggiore è la ridondanza, maggiori saranno le possibilità di individuare e correggere gli eventuali errori per ricostruire il messaggio inviato. Naturalmente, maggiore è la ridondanza, maggiori sono i costi di trasmissione, quindi è necessario trovare un equilibrio fra questi due obiettivi contrastanti.
Esempio 1.1 – Bit di parità
Il sistema più semplice per individuare errori di trasmissione è il controllo di parità. Ad ogni parola di codice si aggiunge un bit, in modo che il numero totale dei bit uguali ad \(1\) sia un numero pari. Ad esempio se la lunghezza fissa del codice è \(5\) abbiamo:
Il ricevitore effettua un controllo sulle parole ricevute, contando il numero degli \(1\). Se questo numero non è pari si è verificato un errore e in genere la stazione ricevente richiede un nuovo invio del messaggio. Chiaramente questo sistema non riesce ad individuare la presenza di errori nel caso che il numero di bit errati sia uguale a \(2\), o in genere ad un numero pari.
Questo metodo, nonostante i suoi limiti e la sua semplicità, è tuttavia ampiamente utilizzato, soprattutto nei casi in cui la probabilità di presenza di più di un errore di trasmissione è molto bassa.
2) Regole di decisione
Un problema fondamentale nella trasmissione su un canale rumoroso consiste nel definire delle regole di decisione ottimali, che permettano di determinare i caratteri trasmessi dalla sorgente con la minima probabilità di errore.
Definizione 2.1 – Regole di decisione
Supponiamo che il carattere che viene ricevuto sia il simbolo \(b_{k}\). Il destinatario deve avere una procedura per stabilire quale è il simbolo trasmesso dalla sorgente. In termini formali una regola di decisione è una funzione
Il concetto è che se viene ricevuta una parola di codice \(b_{k}\), il destinatario deve individuare quale parola \(\sigma(b_{k})\) è stata inviata. Mediante la sua regola di decisione il ricevente quindi assume che \(\sigma(b_{k})=a_{k^{*}}\), dove \(a_{k^{*}}\) è uno dei possibili simboli dell’alfabeto di input. Nel nostro caso il numero delle possibili regole di decisioni è \(r^{s}\), dove \(r=|A|\) e \(s=|B|\). La probabilità che la scelta sia corretta è
\[ P(a_{k^{*}}|b_{k})=Q_{k^{*}k} \]Definiamo inoltre la probabilità congiunta
\[ R_{ik}=P(a_{i},b_{k})=q_{k}Q_{ik} \]Per i simboli \(Q_{ik},R_{ik}\) vedere l’articolo su questo sito.
La probabilità di decodificare correttamente può essere calcolata facendo la media su tutti i simboli ricevuti dal destinatario:
La probabilità di commettere errori nella decodifica è quindi
\[ P_{err}=1-P_{corr}=1-\sum\limits_{k=1}^{s}R_{k^{*}k} \]Il problema consiste nello scegliere una regola di decisione che minimizzi il valore di \(P_{err}\).
Esempio 2.1
Supponiamo di utilizzare un alfabeto sorgente di 4 caratteri \(x,y,z,w\). Possiamo utilizzare la seguente codifica di canale:
L’alfabeto di input è quindi \(A=\{000,110,101,011\}\). Notiamo che in tutti i casi il numero di bit uguali ad \(1\) è pari. L’alfabeto di ouput è costituito da \(8\) parole di codice:
\[ B=\{000,001,010,011,100,101,110,111\} \]È ragionevole scegliere una regola di decisione che coincide con l’identità, nel caso di parole di codice che corrispondono a uno dei valori dell’alfabeto di input. Quindi, ad esempio, \(\sigma(110)=110\) oppure \(\sigma(000)=000\). Il problema è stabilire dei criteri per determinare quali valori di input assegnare nel caso delle parole di codice non appartenenti all’alfabeto di input: \(100,010,001,111\).
Definizione 2.2 – Regola dell’osservatore ideale
La regola dell’osservatore ideale afferma che, dato l’output \(b_{k}\), il ricevente dovrebbe scegliere come parola di codice di input \(\sigma(b_{k})\) quella per la quale la probabilità condizionata che sia stata inviata, dato che viene ricevuta \(b_{k}\), è più grande.
In termini formali si tratta di massimizzare la probabilità a posteriori \(P(a_{i}|b_{k})=Q_{ik}\). Per calcolare la probabilità \(Q_{ik}\) si può utilizzare questa formula:
Questo implica che dobbiamo conoscere sia le probabilità \(p_{i}\) dei simboli dell’alfabeto di input, sia le probabilità \(P_{ij}\) della matrice di transizione del canale. Il problema quindi è equivalente a massimizzare le probabilità congiunte
\[ R_{ik}=P(a_{i},b_{k})=q_{k}Q_{ik} \]per ogni colonna \(k\) della matrice \((R_{ik})\). Una volta calcolata la matrice \((R_{ik})\), si sceglie l’elemento massimo nella colonna \(k\).
Esempio 2.2
Consideriamo il canale binario simmetrico (BSC), nel quali i caratteri inviati sono i bit \((0,1)\). L’equazione matriciale è la seguente:
Per semplicità possiamo porre \(p=p_{0}=P(a=0)\) e \(1-p=p_{1}=P(a=1)\).
La matrice \(R_{ik}\) delle probabilità congiunte è quindi
Se il ricevente riceve il bit \(0\) allora applica la seguente regola:
\[ \begin{array}{l} \sigma(0) = 0 \quad \text{se} \quad p(1-p_{e}) \gt (1-p)p_{e} \\ \sigma(0) = 1 \quad \text{se} \quad p(1-p_{e}) \lt (1-p)p_{e} \\ \end{array} \]In modo analogo si applica la regola per \(\sigma(1)\).
Definizione 2.3 – Regola della massima verosimiglianza
Le regola dell’osservatore ideale è ragionevole, tuttavia la sua applicazione è limitata dalla quantità di informazione necessaria, non sempre disponibile.
Una regola più praticabile è quella della massima verosimiglianza. Il ricevente sceglie la parola di codice \(a_{k^{*}}=\sigma(b_{k})\) tale che
Il criterio della massima verosimiglianza afferma quindi che \(\sigma(b_{k})\) deve essere quella parola di codice per la quale è massima la probabilità di ricevere \(b_{k}\).
Osserviamo che ci può essere più di una parola di codice che soddisfa la condizione di massimo; in tal caso si prende una qualsiasi tra esse.
Esercizio 2.1
Dimostrare che se le parole di codice di input hanno una distribuzione uniforme, cioè \(p_{k}=\dfrac{1}{r}\), allora le due regole di decisione sono equivalenti.
3) Distanza di Hamming
Ricordiamo la definizione di canale prodotto. Siano dati due canali \(K_{1}=(A_{1},B_{1})\) e \(K_{2}=(A_{2},B_{2})\), con matrici di probabilità \(M1,M2\). Gli alfabeti di input e output del canale prodotto \(K=K_{1}\times K_{2}\) sono \(A_{1} \times A_{2}\) e \(B_{1} \times B_{2}\). La matrice di probabilità del canale prodotto è
\[ M_{ii’ kk’}=(M1)_{ik}(M2)_{i’k’} \]In modo equivalente
\[ P(kk’ |ii’) =P(k|i)P(k’|i’) \]La definizione può essere estesa al caso di \(n\) canali, con \(n >2\).
Nel caso di canali binari simmetrici estesi, gli alfabeti di input e output sono stringhe di numeri binari di lunghezza \(n\).
Supponiamo di avere un canale \(K=(A,B)\), dove \(A=\{a_{1},a_{2},\cdots,a_{r}\}\) è l’alfabeto di input e \(B=\{b_{1},b_{2},\cdots,b_{s}\}\) è l’alfabeto di output. Consideriamo ora due parole di codice \(x=x_{1} \cdots x_{n}\) e \(y=y_{1} \cdots y_{n}\) di \(A^{n}\). Ogni parola può essere vista come un vettore dello spazio \(A^{n}\).
Definizione 3.1
La distanza di Hamming \(d(x,y)\) fra due parole di codice è definita come il numero degli indici \(k\) (\(1 \le k \le n)\) tali che \(x_{k} \neq y_{k}\).
Esempio 3.1
Per un codice binario, date due parole di codice \(x= 01101011\) e \(y=11011011\) abbiamo \(d(x,y)=3\).
Si dimostra facilmente il seguente:
Teorema 3.1
Lo spazio \(A^{n}\) con la distanza di Hamming è uno spazio metrico. Precisamente, dati tre vettori \(x,y,z \in A^{n}\) si ha:
Esercizio 3.1
Data una parola di codice \(x \in A^{n}\) calcolare il numero \(t_{k}\) delle parole \(y\) tali che \(d(x,y)=k\) dove \(0 \le k \le n\).
Soluzione: \(\left[ t_{k}=\displaystyle\binom{n}{k}(r-1)^{k}\right]\)
In base all’esercizio precedente possiamo immaginare i vettori a distanza \(k\) da un vettore \(x\) come appartenenti ad una sfera di raggio \(k\) e centro \(x\).
Per semplicità, d’ora in poi assumeremo che il canale sia il canale binario simmetrico BSC, quindi \(A=B=\mathbb{Z}_{2}=\{0,1\}\) e il canale esteso è \(A^{n}=\mathbb{Z}_{2}^{n}\).
Teorema 3.2
Siano dati due vettori \(x,y \in \mathbb{Z}_{2}^{n}\). Se \(d(x,y)=k\) allora
dove \(M_{xy}=P(y|x)\).
Dimostrazione
Supponiamo che venga inviata la parola di codice \(x\) e venga ricevuta la parola \(y\). La probabilità che ci siano \(k\) errori, cioè che \(d(x,y)=k\), è \(p_{e}^{k}\). La probabilità che gli altri \(n-k\) bit siano esatti è \((1-p_{e})^{n-k}\). Quindi la probabilità \(P(y|x)\) è data dal loro prodotto.
Data una parola \(x \in \mathbb{Z}_{2}^{n}\), l’intorno di raggio \(h\) è l’insieme
\[ N_{h}(x)=\{y \in \mathbb{Z}_{2}^{n}| d(x,y) \le h\} \]In modo equivalente l’intorno \(N_{h}(x)\) contiene tutte le parole che possono essere ottenute da \(x\) con un numero di bit errati minore od uguale ad \(h\).
La distanza di Hamming permette di definire un’altra regola di decisione, chiamata la regola dell’intorno più vicino. Precisamente, se al ricevente arriva la parola di codice \(y\), allora sceglie la parola di codice di input che ha distanza minima da \(y\). Nel caso ci siano più parole con la stessa distanza minima, si sceglie una di esse senza distinzione.
Esercizio 3.2
Dimostrare che per i canali BSC la regola della distanza di Hamming è equivalente alla regola della massima verosimiglianza.
Suggerimento
Utilizzare il teorema 3.2. Supporre che \(p_{e} \lt \frac{1}{2}\) e osservare che possiamo scrivere
4) La velocità di trasmissione
L’individuazione e la correzione degli errori di trasmissione si basano sul concetto di ridondanza. I linguaggi naturali sono caratterizzati da un alto grado di ridondanza; questo permette di comprendere in modo corretto anche parole scritte in modo errato. La ridondanza viene sfruttata anche nel mondo delle comunicazioni digitali, per rilevare e correggere eventuali errori. Nel caso della trasmissione digitale vengono inseriti dei bit aggiuntivi in ogni blocco inviato nel canale. L’insieme dei bit aggiuntivi viene scelto in modo da poter applicare degli algoritmi in grado di rilevare errori. La stazione ricevente effettua il controllo e la correzione degli errori, quindi rimuove i bit aggiuntivi. La capacità di rilevare errori e poi eventualmente di correggerli dipende dal numero di bit ridondanti aggiunti.
Supponiamo di utilizzare un codice \(C\) costituito da parole di codice di \(k\) bit. Il numero totale di parole è quindi \(2^{k}\). Ad ogni parola di codice vengono aggiunti \(n-k\) bit di ridondanza. Quindi in input al canale vengono inviati blocchi di lunghezza \(n\) bit. La velocità di trasmissione \(R\) è definita come
Se si utilizza un codice \(r\)-ario, si utilizza il logaritmo in base \(r\).
La velocità di trasmissione soddisfa la relazione
Per ogni intero positivo \(n\) possiamo creare un codice scegliendo in modo casuale \(2^{nR}\) parole. Con \(n\) sufficientemente grande possiamo prendere l’intero più vicino \(\lceil 2^{nR}\rceil\). Il codice ha lunghezza \(n\) e inoltre
\[ \frac{\log_{2}2^{nR}}{n}=R \]Quindi, prendendo dei blocchi di parole abbastanza grandi è possibile ottenere una probabilità di errore arbitrariamente piccola.
5) Il secondo teorema di Shannon
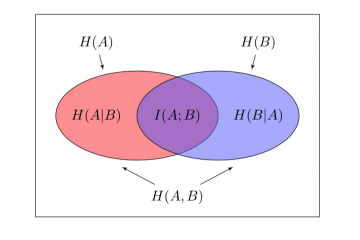
In un articolo precedente abbiamo definito il concetto di capacità di un canale. La capacità di un canale \(K=(A,B)\) è il massimo valore dell’informazione mutua \(I(A;B)\), al variare delle distribuzioni di probabilità dell’alfabeto \(A\), mantenendo invariate le probabilità di transizione:
\[ C = \underbrace{\max}_{p(A)} I(A;B) \]Sia dato un canale discreto \(K=(A,B)\), con \(A= \{a_{1},a_{2},\cdots,a_{r}\}\). Indichiamo con \(p_{k}=P(a_{k})\) la probabilità del simbolo \(a_{k}\). Ricordiamo che l’entropia dell’alfabeto di input è
\[ H_{r}(A)=-\sum\limits_{k=1}^{q}p_{k}\log_{r}p_{k} \]Se \(|A|=r\), per definire l’entropia utilizziamo i logaritmi in base \(r\); nel caso di codici binari, cioè \(A=\{0,1\}\), usiamo il \(\log_{2}\).
Ricordiamo anche che la grandezza \(H(A|B)\) viene chiamata equivocazione di \(A\) rispetto a \(B\) e rappresenta l’incertezza sul simbolo trasmesso che resta una volta conosciuto il simbolo ricevuto. Si può anche interpretare come l’informazione che è stata persa a causa della presenza del rumore nel canale.
Per questi concetti vedere l’articolo su questo sito.
Teorema 5.1 – Secondo teorema di Shannon
Sia dato un canale discreto con capacità \(C\) ed entropia per secondo \(H\).
Se \( H \le C\) allora esiste una codifica tale che è possibile effettuare una trasmissione dei simboli dell’alfabeto di input con probabilità di errore arbitrariamente bassa.
Se \(H \gt C\) allora esiste una codifica tale che l’equivocazione è minore di \(H-C+ \epsilon\), dove \(\epsilon\) è una grandezza reale arbitrariamente piccola. Non esiste una codifica per la quale l’equivocazione è minore di \(H-C\).
Per la dimostrazione vedere il testo di Shannon [1], oppure il testo di Cover [2].
Il caso del canale binario simmetrico (BSC)
Supponiamo di avere un canale binario simmetrico con probabilità di errore uguale a \(p_{e} \lt \frac{1}{2}\). Ricordiamo che la capacità è
Il teorema di Shannon per un canale BSC ha la seguente formulazione:
Teorema 5.2
Siano dati due numeri reali \(\epsilon,\delta \gt 0\). Prendendo \(n\) abbastanza grande, esiste un codice \(K \subset \mathbb{Z}_{2}^{n}\) tale che la sua velocità \(R\) soddisfa
e inoltre la probabilità di errore, con il metodo della massima verosimiglianza, soddisfa
\[ p_{err} \lt \delta \]Possiamo riassumere il contenuto del teorema di Shannon in questo modo:
- la capacità \(C\) di un dato canale rappresenta la massima velocità di trasmissione su quel canale;
- per ogni velocità di trasmissione \(R \lt C\), l’errore di trasmissione può essere reso piccolo a piacere;
- maggiore è la riduzione dell’errore, maggiori sono i costi e i tempi della comunicazione.
6) Codici binari lineari
Per introdurre i codici lineari è necessario conoscere i concetti fondamentali dell’algebra lineare. Per una introduzione vedere [5].
I codici lineari sono codici algebrici su un campo. Consideriamo l’insieme \(Z_{2}=\{0,1\}\). Questo insieme assume la struttura di campo con le usuali operazioni binarie di addizione e moltiplicazione:
L’insieme \(Z_{2}^{n}\) è costituito da stringhe binarie di lunghezza \(n\). Possiamo scrivere una stringa come \((x_{1}x_{2}\cdots x_{n})\). Dal punto di vista algebrico è uno spazio vettoriale di dimensione \(n\) sul campo \(Z_{2}\).
Su uno spazio vettoriale sono definite due operazioni, addizione di due vettori e moltiplicazione scalare tra un vettore e un elemento del campo base. Nel nostro caso abbiamo:
Ricordiamo che una base \(\{e_{1}, \cdots, e_{n}\}\) di uno spazio vettoriale di dimensione \(n\) sul campo \(\mathbb{Z}_{2}\) è un insieme di vettori linearmente indipendenti che generano l’intero spazio. Cioè per ogni vettore \(x \in V\) si ha
\[ x = a_{1}e_{1}+ \cdots + a_{n}e_{n} \quad a_{k} \in \mathbb{Z}_{2} \]Un sottospazio vettoriale è un sottoinsieme \(S\) di uno spazio vettoriale \(V\) che è chiuso rispetto alle due operazioni di addizione e moltiplicazione scalare. Per le ipotesi se un vettore \(x \) appartiene a \(S\) allora il suo opposto \(-x = (-1)\cdot x\) appartiene a \(S\). Inoltre anche il vettore nullo appartiene a \(S\) in quanto se \(x \in S\) allora anche \(o = o \cdot x\) sta in \(S\).
Ogni sottospazio vettoriale di dimensione finita è generato da una famiglia finita di vettori. In uno spazio vettoriale \(V\) di dimensione \(n\), per ogni intero \(0 \le k \le n\) esiste un sottospazio vettoriale di dimensione \(k\). Per questo basta scegliere come base un insieme di \(k\) vettori linearmente indipendenti dello spazio \(V\).
Si possono scegliere diverse basi per uno spazio vettoriale. La base più semplice per lo spazio \(Z_{2}^{n}\) è la base standard, costituita da \(n\) vettori \(u_{k}\), con \(k=1,2,\cdots,n\). Ogni vettore \(u_{k}\) ha la coordinata \(k\)-esima uguale ad \(1\) e tutte le altre uguali a \(0\).
Definizione 6.1
Un codice binario lineare è un sottospazio vettoriale dello spazio \(Z_{2}^{n}\).
Esempio 6.1
Consideriamo il sottoinsieme \(C=\{000,110,011,111\}\) di \(Z_{2}^{n}\). Non è un sottospazio vettoriale e quindi non è un codice lineare, in quanto ad esempio \(110+011=101\) non appartiene all’insieme \(C\).
Supponiamo che \(C\) sia un codice binario lineare, e quindi un sottospazio di \(Z_{2}^{n}\) di dimensione \(k\), con \(0\le k \le n\). Il numero \(k\) rappresenta il numero di elementi della base di \(C\) e viene chiamato dimensione del codice lineare. Ogni elemento di \(C\) può quindi essere espresso come combinazione lineare di elementi della base. Il numero di vettori del sottospazio \(C\) è quindi \(2^{k}\). La velocità di trasmissione del codice è
\[ R=\frac{\log_{2}|C|}{n}=\frac{k}{n} \]Definizione 6.2
Dato un codice \(C\), la distanza minima \(d(C)\) è la più piccola distanza di Hamming di tutte le coppie di parole di codice:
Un codice binario lineare su \(Z_{2}^{n}\) viene in genere indicato con il simbolo \([n,k,d]\) oppure con \([n,k]\).
Esempio 6.2
Consideriamo le seguenti parole del codice binario \(C\) di lunghezza \(5\):
È facile verificare che la distanza minima è \(d(C)=3\). Si tratta di un sottospazio vettoriale; una base è costituita dai vettori \(x_{2},x_{3}\). Quindi \(C\) è un codice binario lineare \([5,2,3]\) su \(\mathbb{Z}_{2}\).
Definizione 6.3 – Peso di Hamming
Sia \(x= x_{1} \cdots x_{n}\) una parola di codice in \(Z_{2}^{n}\). Il peso di Hamming \(w(x)\) è il numero di \(1\) presenti nella parola. In modo equivalente il peso è dato da
dove \(0\) denota il vettore nullo \(00\cdots 0\).
Esercizio 6.1
Dimostrare che
Indichiamo con \(w(C)\) il più piccolo dei pesi delle parole di codice non nulle:
\[ w(C)= \min \{w(x): x \in C, x \neq 0\} \]Teorema 6.1
Dato un codice lineare \(C\) su \(Z_{2}^{n}\), la distanza minima \(d(C)\) soddisfa
Dimostrazione
Siano \(x,y\) due parole di codice con \(d(x,y)=d(C)\). Allora
D’altra parte, per qualche parola di codice \(z\) abbiamo
\[ w(C) = w(z)=d(z,0) \ge d(C) \]Quindi deve essere \(d(C)=w(C)\).
6.1) Correzione degli errori
Un codice a correzione di errore (ECC) è un sistema di codifica binaria dei messaggi che permette di ricostruire il messaggio originale, anche in presenza di errori di trasmissione.
Supponiamo di utilizzare come regola di decisione la regola della distanza minima. È facile verificare che vale il seguente teorema:
Teorema 6.2
Sia dato un codice lineare \(C\) con \(d(C) \ge 2r+1\). Allora per ogni coppia di parole distinte gli intorni \(N_{r}(x),N_{r}(y)\) sono disgiunti.
Vediamo ora le condizioni necessarie per creare un codice a correzione di errore.
Teorema 6.3
Supponiamo che la sorgente trasmittente uttilizzi un codice \(C\) con \(d(C) \ge 2r+1\) e il ricevente utilizzi la regola della distanza minima. Allora, se il numero di errori di trasmissione non è superiore a \(r\), è possibile ricostruire ogni parola ricevuta in modo corretto.
Dimostrazione
Sia \(x\) la parola di codice inviata e \(z\) la parola ricevuta. Se non sono presenti più di \(r\) errori di trasmissione allora \(z \in N_{r}(x)\). Per il teorema precedente, \(z\) non appartiene a nessun altro intorno \(N_{r}(y), y \neq x\). Quindi \(d(x,z) \lt d(y,z) \) per tutte le parole di codice \(y \neq x\), e per la regola della distanza minima assegniamo la parola \(x\) a quella ricevuta \(z\).
Definizione 6.4
Un codice binario \(C\) si chiama codice a correzione di errore con parametro \(r\) se \(d(C) \ge 2r+1\).
Il codice dell’esempio 6.2 è un codice binario a correzione di errore con parametro \(1\).
Nota
Un problema più semplice è costituito dalla rilevazione degli errori senza la correzione. Per rilevare \(r\) errori è necessario un codice \(C\) tale che \(d(C)=r+1\).
6.2) La matrice generatrice di un codice lineare
Un codice lineare \([n,k,d]\) su \(Z_{2}^{n}\) contiene \(2^{k}\) parole di codice. Il flusso dei dati da trasmettere viene suddiviso in blocchi di lunghezza \(k\). Ad ogni blocco vengono aggiunti \(n-k\) bit per la rilevazione e controllo degli errori. Vengono quindi trasmessi sul canale dei blocchi di lunghezza \(n\). La codifica dei messaggi di input è equivalente quindi ad una trasformazione lineare \(\psi\) dallo spazio \(Z_{2}^{k}\) allo spazio \(Z_{2}^{n}\):
\[ \psi: Z_{2}^{k} \to Z_{2}^{n} \]Esempio 6.3
Supponiamo di codificare dei blocchi di \(3\) bit con parole di codice di lunghezza \(6\), quindi con un codice \([6,3]\). Dato un blocco \(a=a_{1}a_{2}a_{3}\), la parola codice corrispondente \(x=x_{1}x_{2}x_{3}x_{4}x_{5}x_{6}\) è ottenuta ponendo
Lo stesso risultato può esser ottenuto mediante la seguente trasformazione lineare:
\[ \begin{pmatrix} x_{1} & x_{2} & x_{3} &x_{4} &x_{5} &x_{6} \end{pmatrix} = \begin{pmatrix} a_{1} &a_{2} &a_{3} \end{pmatrix} \cdot \begin{pmatrix} 1 &0 & 0 & 1 & 0 & 1 \\ 0 &1 & 0 & 1 & 1 & 0 \\ 0 &0 & 1 & 0 & 1 & 1 \\ \end{pmatrix} \]Ad esempio la parola di codice corrispondente al blocco \(a_{1}a_{2}a_{3}=111\) è \(111000\).
Esercizio 6.2
Calcolare le parole di codice corrispondenti agli \(8\) possibili blocchi di input dell’esempio precedente.
Come è noto dall’algebra lineare, ogni trasformazione lineare può essere rappresentata tramite una matrice \(G\), chiamata matrice generatrice, che moltiplicata per il vettore di input fornisce il vettore di output. Nel nostro caso abbiamo una matrice \(G(k,n)\), con \(k\) righe e \(n\) colonne:
\[ \psi(x) = xG \quad x \in Z_{2}^{k} \]In questa notazione i vettori \(x\) e \(\psi(x)\) vanno intesi come vettori riga.
Ogni riga della matrice corrisponde ad un elemento della base del codice lineare. La matrice generatrice dipende dalla scelta della base per lo spazio vettoriale.
Se facciamo una permutazione delle colonne della matrice \(G\) otteniamo un altro codice, che tuttavia differisce soltanto nell’ordine dei simboli nelle parole di codice. I parametri del codice \([n,k,d]\) non cambiano. In questo caso diciamo che i due codici sono equivalenti.
Esempio 6.3
Consideriamo il codice lineare binario \([6,3,3]\). Sia data la seguente matrice generatrice \(G\):
L’operazione di codifica consiste nel moltiplicare ogni parola di codice di lunghezza \(k=3\) per la matrice \(G\). Ad esempio per la parola di codice 010 abbiamo
\[ \begin{pmatrix} 0 &1 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 &0 & 0 & 1 & 0 & 1 \\ 0 &1 & 0 & 1 & 1 & 0 \\ 0 &0 & 1 & 1 & 1 & 1 \\ \end{pmatrix} = \begin{pmatrix} 0 &1 & 0 & 1 & 1 & 0 \\ \end{pmatrix} \]In modo simile si calcolano gli altri codici.
6.3) La matrice di controllo di parità di un codice lineare
Oltre alla matrice generatrice, esiste un’altra matrice associata ad un codice binario lineare, chiamata matrice di controllo di parità.
Supponiamo che \(C\) sia un codice lineare \([n,k,d]\), cioè un sottospazio di dimensione \(k\). Si definisce complemento ortogonale di \(C\), e si indica con \(C^{\perp}\), il sottospazio di dimensione \(n-k\) contenente i vettori che sono tutti ortogonali ad ogni vettore di \(C\). Come è noto dall’algebra lineare, tale sottospazio può essere definito anche mediante le soluzioni di un sistema di \(n-k\) equazioni lineari. La matrice di questo sistema di equazioni è una matrice \(H(n-k,n)\) con \(n-k\) righe e \(n\) colonne; viene chiamata matrice di controllo di parità per il codice \(C=[n,k,d]\).
In base alla definizione, gli elementi del codice \(C\) sono definiti dalla seguente equazione:
dove la \(H^{T}\) è la matrice trasposta di \(H\), ottenuta scambiando le righe con le colonne.
Esercizio 6.2
Determinare le parole di codice associate alla seguente matrice di controllo di parità:
Soluzione
Impostare l’equazione \(xH^{T}=0\), con \(x=x_{1}x_{2}x_{3}x_{4}\). Abbiamo due equazioni:
Considerando le varie possibilità, si trovano \(4\) parole di codice possibili:
\[ 0000-0101-1011-1110 \]Si tratta di un codice binario \([4,2,2]\).
6.4) Relazione fra matrice generatrice e matrice di controllo di parità
La relazione fra la matrice di parità \(H\) e la matrice generatrice \(G\) è data dal seguente teorema:
Teorema 6.4
Sia dato un codice binario lineare \([n,k]\) su \(\mathbb{Z}_{2}^{n}\), con matrice di parità \(H\) e matrice generatrice \(G\). Allora la matrice \(H\) ha \(n-k\) righe e \(n\) colonne e vale la seguente relazione:
7) Codici di Hamming
Il secondo teorema di Shannon afferma che esistono dei codici a blocchi che permettono di trasmettere con velocità di informazione inferiore alla capacità del canale e con probabilità di errore arbitrariamente piccola. Naturalmente la lunghezza dei blocchi deve essere abbastanza grande, per ridurre l’errore.
I codici di Hamming sono i tipi più semplici di codici lineari con controllo di parità, che permettono di correggere gli errori sui singoli bit.
Sia dato un intero \(r \ge 2\) e una matrice \(H(r,2^{r}-1)\) sul campo \(\mathbb{Z}_{2}\). I vettori colonna della matrice siano tutti i \(2^{r}-1\) vettori non nulli dello spazio vettoriale \(\mathbb{Z}_{2}^{r}\).
Esempio 7.1
Nel caso \(r=3\) possiamo avere
I vettori colonna sono linearmente indipendenti.
La matrice \(H_{r}\) può essere considerata come matrice di controllo di parità di un codice binario lineare. La lunghezza del codice è uguale a \(2^{r}-1\), il numero delle colonne. La dimensione è \(k=2^{r}-1-r\).
Definizione 7.1
Il codice lineare \([2^{r}-1,2^{r}-1-r]\) con matrice di parità \(H_{r}\) viene chiamato codice di Hamming con ridondanza \(r\) e indicato in genere con \(\text{Ham}(r,2)\).
Nel caso dell’esempio 7.1 abbiamo un codice di Hamming \(\text{Ham}(7,2)\) o semplicemente \(H_{7}\). La dimensione è \(7-3=4\). Si tratta di un codice \([7,4]\).
Il simbolo \(\text{Ham}(r,2)\) denota tutti i codici con ridondanza \(r\) sul campo \(\mathbb{Z}_{2}\). Per ogni coppia di parametri \((r,2)\) esistono diverse possibilità di scelta della matrice, permutando le colonne. Tuttavia i vari codici che si ottengono sono equivalenti.
Teorema 7.1
Tutti i codici di Hamming hanno distanza minima uguale a \(3\) e quindi sono in grado di correggere i singoli errori.
Dimostrazione
Siano \(x,y\) due parole di codice di codice di Hamming \(C\), con matrice di controllo di parità \(H\). Anche la parola \(x-y \in C\), in quanto il codice lineare è uno spazio vettoriale. Se la distanza \(d(x,y)=1\) allora il prodotto \((x-y)H^{T}\) è una colonna di \(H\). Questo implica una contraddizione; infatti le colonne di \(H\) sono tutte non nulle, ma \((x-y)H^{T}=0\), essendo \(x-y\) una parola del codice \(C\).
Se \(d(x,y)=2\) allora \((x-y)H^{T}=0\) se e solo se ci sono due colonne di \(H\) linearmente dipendenti. Ma questo non è possibile per la stessa definizione della matrice \(H\). Quindi la distanza \(d(x,y) \ge 3\), per ogni coppia di parole di codice \((x,y)\). Per il teorema 6.3 i codici di Hamming sono in grado di correggere i singoli errori.
Esercizio 7.1
Quanti bit di controllo sono necessari se il codice a correzione di errore di Hamming viene usato per rilevare errori di bit singoli in una parola di dati a 1024 bit ?
Soluzione: 11 bit di controllo.
Teorema 7.2
In un codice binario di Hamming \([n,k,3]\), ogni parola di \(\mathbb{Z}_{2}^{n}\) è una parola di codice esatta, oppure ha una distanza pari ad \(1\) da una parola di codice esatta.
Dimostrazione
Il numero delle parole di codice è \(2^{k}\). Per ogni parola codice \(c\) si ha \(N_{1}(c)=n+1\). Poiché la distanza minima è uguale a \(3\), gli intorni di tutte le parole sono disgiunti. Inoltre abbiamo
Quindi gli intorni di raggio \(1\) delle \(2^{k}\) parole di codice sono disgiunti e ricoprono completamente l’insieme \(\mathbb{Z}_{2}^{n}\).
7.1) La decodifica di un codice
Data una parola ricevuta \(y\), il problema della decodifica consiste nel trovare una parola di codice \(x\) che ha distanza di Hamming minima da \(y\). Il problema può essere semplificato mediante la tecnica di decodifica della sindrome.
Definizione 7.2
Sia dato un codice \(C\) \([n,k]\) su \( \mathbb{Z}_{2}^{n}\) e sia \(x\) un vettore di \(\mathbb{Z}_{2}^{n}\). Si chiama coset di \(C\) relativo ad \(x\) l’insieme
Un coset quindi contiene \(2^{k}\) elementi.
Esercizio 7.2
Dimostrare le seguenti proprietà dei coset:
- se \(y \in x+C\) allora i due coset \(x+C\) e \(y+C\) coincidono
- ogni vettore \(x \in \mathbb{Z}_{2}^{n}\) appartiene ad un unico coset
- ogni coset contiene \(2^{k}\) elementi
- il numero totale dei coset è \(2^{n-k}\)
Si chiama coset leader ogni vettore che ha peso minimo in quel particolare coset.
La tabella di enumerazione dei coset
Ai fini della decodifica è utile costruire una tabella per enumerare i coset. La tabella è costituita da \(2^{n-k}\) righe e \(2^{k}\) colonne. Nella prima riga si scrivono i vettori del codice \(C\), che possiamo pensare associato al coset leader \(w_{1}=0\). Per la seconda riga si sceglie come coset il vettore di peso minimo \(w_{2}\) fra quelli non ancora inseriti nella tabella. E così via. Gli elementi sulla prima colonna della matrice canonica sono i coset leader.
Mediante questa tabella è possibile creare una corrispondenza biunivoca fra un generico vettore \(x\) e il coset leader relativo alla riga che contiene \(x\).
Un vettore \(y\) ricevuto dal destinatario viene decodificato con la parola presente nella prima riga della tabella, corrispondente alla colonna nella quale si trova \(y\).
Per valori grandi di \(n\) l’utilizzo della tabella di enumerazione dei coset per la decodifica può risultare piuttosto complesso. Per descrivere un sistema più semplice e veloce introduciamo il concetto di sindrome di una parola di codice.
Definizione 7.2
Sia \(H\) la matrice di parità di un codice e \(w\) una parola ricevuta dal destinatario. La sindrome di \(w\) è
L’insieme delle sindromi costituisce un sottospazio vettoriale di dimensione \(2^{n-k}\), e gli elementi di tale sottospazio possono essere posti in corrispondenza biunivoca con i coset leader della tabella di enumerazione dei coset.
La sindrome permette di rivelare gli errori presenti nel vettore ricevuto \(w\).
Esercizio 7.3
Dimostrare che due parole ricevute \(y_{1},y_{2}\) hanno la stessa sindrome se e solo se
dove \(c\) è una parola valida del codice.
Dimostrazione
Per ipotesi abbiamo \(y_{1}H^{T}= y_{2}H^{T}\) e quindi \((y_{1}-y_{2})H^{T}=0\). Quindi \(y_{1}-y_{2}=c\), dove \(c\) è una parola valida del codice.
Tabella di decodifica
Al posto della tabella completa di enumerazione dei coset si può utilizzare la tabella di decodifica costituita da due colonne: la colonna dei coset leader e la colonna delle rispettive sindromi.
Definiamo un vettore di errore \(e\) costituito da \(n\) bit. I bit uguali ad \(1\) in questo vettore indicano la posizione degli errori di trasmissione. Ad esempio, se \(x=(11001)\) e \(y=(10011)\) allora \(e=(01010)\).
Quindi, se \(x\) è il vettore inviato e \(y\) quello ricevuto possiamo scrivere
Per stimare la parola di codice trasmessa è sufficiente quindi calcolare il vettore di errore e sommarlo al vettore ricevuto.
L’algoritmo per stimare la parola di codice trasmessa è il seguente:
- calcolare la sindrome \(s(y)=yH^{T}\);
- identificare l’errore \(e\) nella tabella, prendendo la parola in corrispondenza della stessa sindrome. Se non fosse possibile trovare il valore della sindrome, allora la parola non è decodificabile;
- calcolare la parola di codice inviata \(x=y+e\).
Esempio 7.2
Consideriamo il codice lineare \([7,4]\) su \(\mathbb{Z}_{2}\) con la seguente matrice generatrice:
e la seguente matrice di parità:
\[ H= \begin{pmatrix} 0 &1 & 1&1 &1 & 0 & 0 \\ 1 &0 & 1&1 &0 & 1 & 0 \\ 1 &1 & 1&0 &0 & 0 & 1 \\ \end{pmatrix} \]La tabella di decodifica è la seguente:
\[ \begin{array}{l} \text{coset leader} \quad \text{sindrome} \\ 0000000 \quad \quad \quad 000 \\ 0000001 \quad \quad \quad 001 \\ 0000010 \quad \quad \quad 010 \\ 0000100 \quad \quad \quad 100 \\ 0001000 \quad \quad \quad 110 \\ 0010000 \quad \quad \quad 111 \\ 0100000 \quad \quad \quad 101 \\ 1000000 \quad \quad \quad 011 \\ \end{array} \]Quando viene ricevuto un vettore \(y\), viene calcolata la sindrome \(s(y)\). Ad esempio, se \(y=0110110\) allora \(s(y)=100\). Il coset leader corrispondente è \(a=0000100\). Quindi il vettore ricevuto y viene decodificato come \(x=y+a=0110010\).
Oltre ai codici di Hamming sono stati sviluppati altri codici più sofisticati, in grado di garantire una maggiore efficienza e gestire trasmissioni in cui è presente più di un errore nel blocco dei dati. Tra questi ricordiamo i codici di Reed-Solomon, usati in particolare nelle trasmissioni wireless e nei dispositivi di memoria, oppure i codici di Reed-Muller e i codici polari, usati per le trasmissioni con i satelliti e le reti 5G. Per questi argomenti più avanzati vedere [4].
Conclusione
La teoria dell’informazione di Shannon, illustrata in questo articolo e nei due precedenti, costituisce la base della moderna civiltà dei computer e delle reti di telecomunicazione, ormai diffuse in tutti i paesi. Shannon può essere giustamente considerato uno dei padri della moderna società dell’informazione.
Bibliografia
[1]C. E. Shannon – The Mathematical Theory of Communication (The University of Illinois Press)
[2]T. Cover – Elements of Information Theory (Wiley)
[3]David MacKay – Information Theory, Inference and Learning Algorithms (Cambridge U.P.)
[4]Todd K. Moon – Error Correction Coding: Mathematical Methods and Algorithms (Wiley)
[5]S. Lipschutz – Schaum’s Outlines Linear Algebra (McGraw-Hill)
0 commenti