La teoria dei grafi studia le strutture costituite da un insieme di punti o vertici, collegati fra loro tramite archi o spigoli. E’ uno strumento importante per la creazione di modelli e la soluzione di problemi decisionali. I suoi campi di applicazioni sono molteplici: teoria dei giochi, ricerca operativa, informatica, scienze sociali, reti elettriche, rete internet, ecc.
La nascita della teoria dei grafi può essere fatta risalire al \(1736\), quando Eulero risolse il famoso problema dei \(7\) ponti di Königsberg. Il problema consiste nel trovare un cammino che attraversa ognuno dei ponti una ed una sola volta. Vedremo in un paragrafo successivo la soluzione di Eulero.
In questo articolo introdurremo i concetti e le definizioni di base della teoria dei grafi. Quindi applicheremo questi concetti per descrivere alcune proprietà del grafo del Web, in cui i nodi sono le pagine HTML e gli archi sono i collegamenti ipertestuali (link) fra le pagine. Si tratta di un grafo di dimensioni enormi, in continua espansione. Ormai contiene alcuni miliardi di nodi e centinaia di miliardi di collegamenti.
1) I grafi
Un grafo non orientato è una coppia \(G = (V, E)\), dove \(V\) è un insieme i cui elementi si chiamano vertici o nodi, mentre \(E\) è un sottoinsieme del prototto cartesiano \(V \times V\), cioè un insieme di coppie non ordinate di vertici. Gli elementi di \(E\) si chiamano spigoli o lati o archi. Si usano le seguenti notazioni \(V=V(G)\) e \(E=E(G)\) per indicare gli insiemi dei vertici e degli archi di un grafo \(G=(V,E)\).
I vertici vengono indicati in genere con le lettere o con dei numeri. Un arco che collega due vertici \(u,v\) può essere indicato con il simbolo \(uv\) o con la coppia non ordinata \((u,v)\).
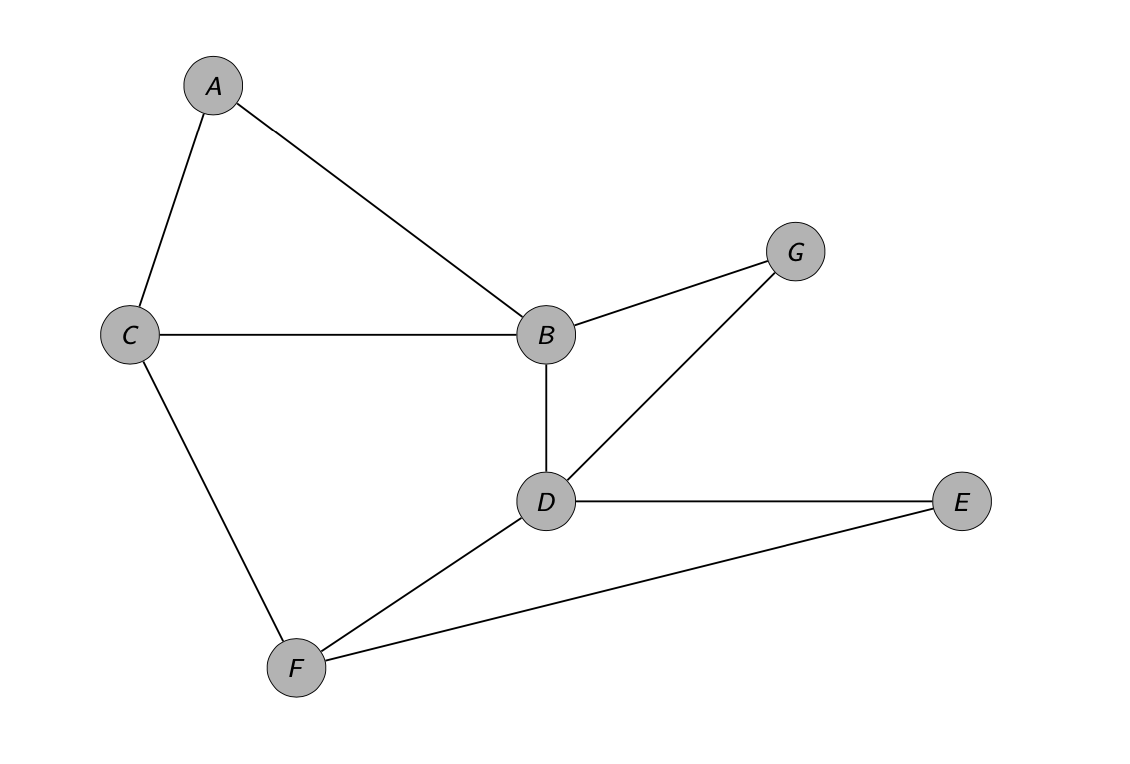
L’ordine di un grafo è il numero dei vertici, mentre la dimensione di un grafo è data dal numero degli archi. In questo articolo consideriamo grafi con un numero finito di vertici e di archi. Un grafo \(G\) di ordine \(n\) e dimensione \(m\) può essere indicato con la seguente notazione:
\[ \begin{array}{l} V(G) = \{v_{1}, \cdots, v_{n}\} \\ E(G)=\{e_{1}, \cdots, e_{m}\} \end{array} \]Tipologie di grafi
Se esistono almeno due archi distinti con gli stessi estremi il grafo viene chiamato multigrafo. Un arco che ha i due estremi coincidenti viene chiamato cappio.
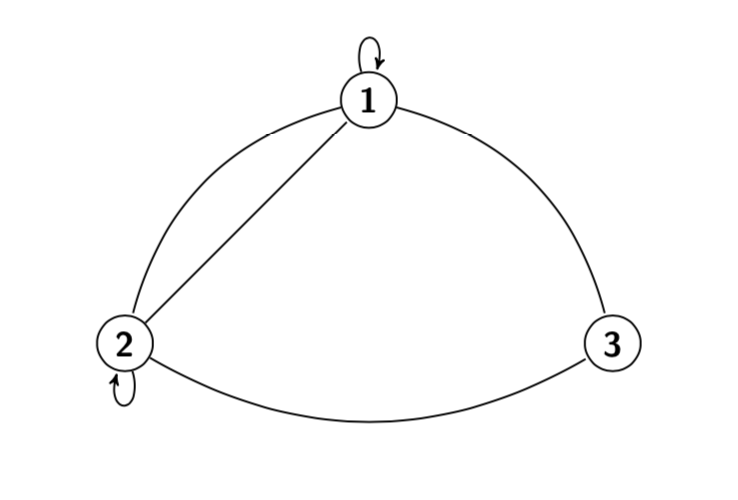
Un grafo non orientato si dice semplice se per ogni coppia di vertici \(u,v\) esiste al massimo un solo arco \((u,v) \in E(G)\) e non esistono cappi.
Alcune proprietà dei grafi semplici
Dato un arco \((x,y)\), i vertici \(x,y\) vengono chiamati gli estremi dell’arco. I vertici dell’arco \((x,y)\) vengono detti adiacenti, mentre il vertice \(x\) (oppure \(y\)) e l’arco \((x,y)\) vengono detti incidenti. Usiamo la notazione \(x \sim y\) per indicare che due nodi sono adiacenti.
L’intorno di un vertice \(v\), indicato con \(N(v)\), è l’insieme dei vertici adiacenti a \(v\):
L’intorno di un insieme di vertici è l’unione degli intorni di tutti i vertici.
In un grafo il grado di un vertice \(v\), indicato con \(\deg(v)\) è il numero di archi incidenti su di esso. Se \(\deg(v) = 0\) allora il vertice \(v\) si dice isolato. Il massimo grado di un grafo \(G\), indicato con \(\Delta(G)\) è
In modo simile si definisce il minimo grado \(\delta(G)\).
Un grafo si dice regolare se tutti i vertici hanno lo stesso grado, cioè se \(\Delta(G)=\delta(G)\).
Teorema 1.1
In un grafo non orientato \(G=(V,E)\) risulta
Cioè la somma dei gradi dei vertici è un numero pari, uguale al doppio del numero degli archi.
Dimostrazione
Osserviamo che ogni spigolo del grafo collega due vertici, aumentando di \(1\) il grado di ciascuno dei due estremi. Quindi la somma dei gradi di tutti i vertici del grafo è pari al doppio degli spigoli del grafo stesso.
Esercizio 1.1
Dimostrare che in ogni grafo \(G=(V,E)\) il numero dei nodi che hanno grado dispari è pari.
La sequenza dei gradi di un grafo è la sequenza monotona non crescente dei gradi dei suoi vertici (si può anche utilizzare l’ordine opposto, cioè monotona non decrescente). Ad esempio la sequenza dei gradi del grafo di Figura 1 è \([4,4,3,3,2,2,2]\).
Definizione 1.1 – Sottografo
Un sottografo \(H\) di un grafo \(G = (V, E) \) è un grafo tale che
Notiamo che i sottoinsiemI \(V(H),E(H)\) non posso essere insiemi qualsiasi. Poiché \(H\) deve essere un grafo, tutti gli archi in \(E(H)\) devono avere come estremi dei vertici presenti in \(V(H)\).
Dato un grafo \(G=(V,E)\) e un sottoinsieme \(V_{1} \subset V\), il sottografo \(G_{1}=(V_{1},E(V_{1}))\) si dice indotto da \(V_{1}\) se contiene tutti gli archi di \(G\) con entrambi gli estremi in \(V_{1}\). In altri termini in un sottografo indotto sono presenti tutti gli archi del grafo che collegano i vertici di \(V_{1}\).
Un grafo si dice completo se ogni coppia di vertici sono adiacenti. Indichiamo con \(K_{n}\) un grafo completo di grado \(n\).
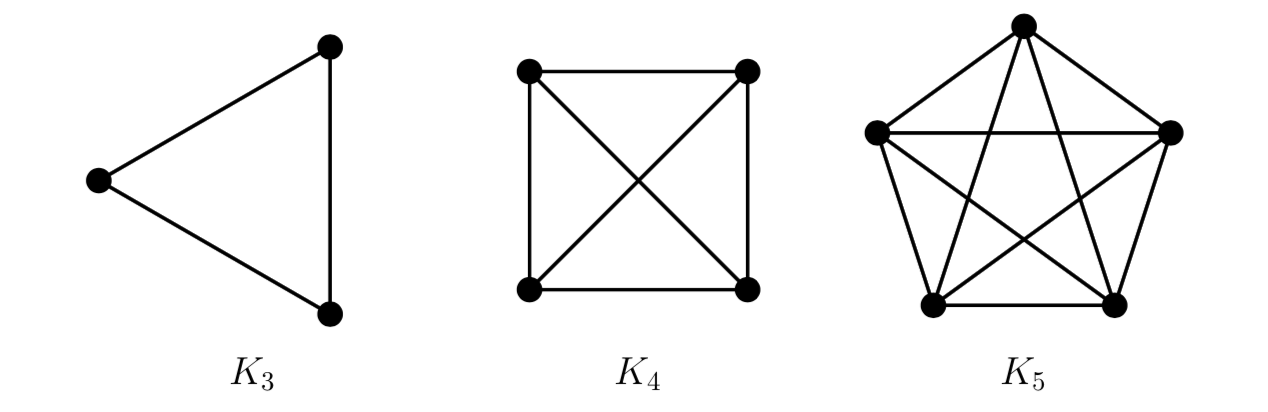
Esercizio 1.2
Dimostrare che il numero di archi di un grafo semplice completo \(K_{n}\) è uguale a \(\dfrac{n(n-1)}{2}\).
2) Rappresentazioni dei grafi
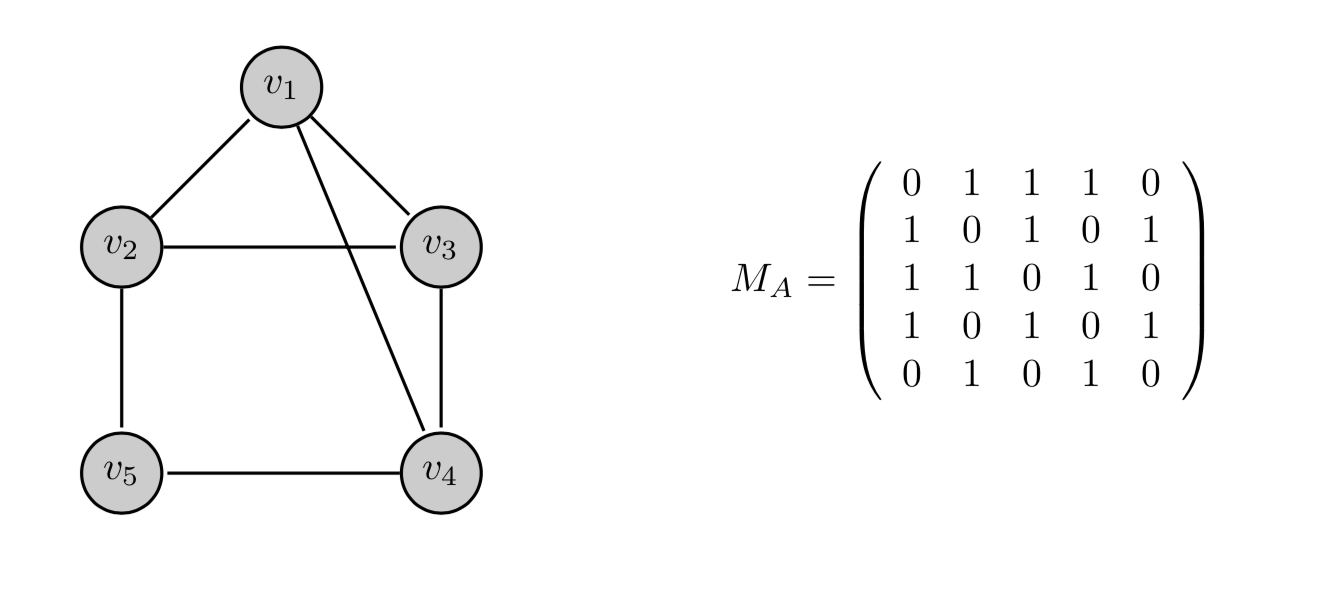
Esistono vari modi di rappresentare un grafo \(G=(V,E)\) di ordine \(n\). Un primo tipo di rappresentazione è dato dalla matrice di adiacenza, una matrice quadrata \(M_{A}\) con \(n\) righe e \(n\) colonne, definita in questo modo:
\[ M_{A}(i,j) = \begin{cases} 1 \quad \text{se } (v_{i},v_{j}) \in E(G) \\ 0 \quad \text{altrimenti} \end{cases} \]dove \(V(G)=\{v_{1}, \cdots,v_{n}\}\).
Nel caso di un grafo non orientato, naturalmente la matrice di adiacenza è simmetrica rispetto alla diagonale principale, cioè \(M(i,j)=M(j,i)\).
In un grafo con \(n\) vertici, abbiamo \(n!\) diverse possibilità di numerare i vertici. Comunque la matrice di adiacenza è univocamente determinata, a parte l’ordine delle righe e delle colonne.
Esercizio 2.1
Dimostrare che nella matrice di adiacenza di un grafo semplice non orientato la somma di tutti gli elementi è uguale al doppio del numero degli archi del grafo.
Un altro modo di rappresentare un grafo è la matrice di incidenza nodi-archi. Si tratta di una matrice \(M_{I}(n \times m)\), dove \(n\) è il numero dei nodi e \(m\) è il numero degli archi, tale che
\[ M_{I}(i,j) = \begin{cases} 1 \quad \text{se } e_{j} \text{ è incidente su } v_{i} \\ 0 \quad \text{altrimenti} \end{cases} \]Ogni riga rappresenta un nodo, mentre ogni colonna rappresenta un arco. Ad esempio la matrice di incidenza del grafo seguente è
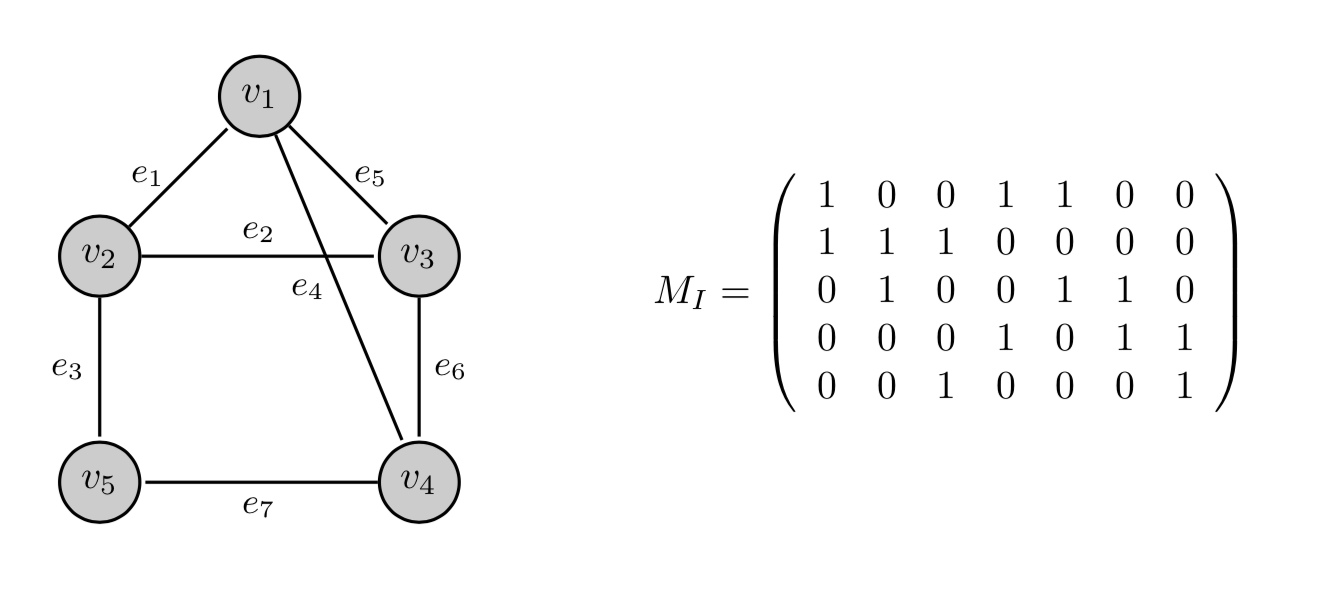
Esercizio 2.2
Dimostrare che nella matrice di incidenza di un grafo semplice non orientato la somma di tutti gli elementi è uguale al doppio del numero degli archi del grafo.
Infine un’altra tecnica molto utile è l’utilizzo delle liste di adiacenza. Per ogni vertice \(u \in V\) si crea una lista \(Adj(u)\) contenente tutti i vertici \(v \in V\) collegati al vertice \(u\).
Ogni tipo di rappresentazione presenta dei vantaggi e degli svantaggi, a seconda del tipo di elaborazione che viene fatta.
Per uno studio approfondito delle rappresentazioni dei grafi e dei principali algoritmi di ricerca vedete il testo di Cormen [1].
3) Cammini e connettività dei grafi
Definizione 3.1
Sia dato un insieme di vertici \(\{v_{0},v_{1}, \cdots,v_{k}\}\). Un cammino semplice (path) è un grafo \(P=(V,E)\) così definito:
Un cammino connette una sorgente \(v_{0}\) con una destinazione \(v_{k}\). Il numero \(k\) (numero di lati) è la lunghezza del cammino. Possiamo vedere anche un cammino di lunghezza \(k\) come una sequenza di \(k\) archi a due a due adiacenti. Un cammino si può indicare semplicemente con la notazione \(P=v_{0}v_{1} \cdots v_{k}\). Se sorgente e destinazione coincidono il cammino si dice chiuso.
Definizione 3.2
Una passeggiata (walk) fra due nodi \(v_{0},v_{k}\) in un grafo \(G=(V,E)\) è una successione finita di vertici e lati:
dove \(e_{i}=v_{i-1}v_{i},\ 0 \lt i \le k\).
I vertici e i lati di una passeggiata non sono necessariamente distinti. Se i vertici iniziale e finale coincidono, la passeggiata si dice chiusa. Un cammino è una passeggiata con tutti i vertici distinti.
Definizione 3.3
Un percorso (trail) in un grafo G è una passeggiata in cui non ci sono lati ripetuti. Un circuito è un percorso in cui i vertici iniziale e finale coincidono. Ovviamente in un percorso ci possono essere dei vertici ripetuti.
Un ciclo semplice \(C_{k}\) di lunghezza \(k\) è un circuito \((v_{0},v_{1}, \cdots,v_{k-1})\) costituito da \(k\) vertici distinti e da \(k\) spigoli. Un cappio è un ciclo di lunghezza \(1\). Un grafo privo di cicli si dice aciclico.
La distanza fra due vertici \(u,v\), indicata con \(d(u,v)\), è la lunghezza, calcolata come numero di archi, del cammino semplice più breve fra i due vertici.
E’ facile verificare che la distanza fra due vertici soddisfa gli assiomi di un spazio metrico:
3.1) Grafi connessi
Due vertici \(u,v\) di un grafo di dicono connessi se esiste un cammino da \(u\) a \(v\). Si dice anche che la coppia di vertici \(u,v\) è connessa.
Un grafo \(G\) si dice connesso se ogni coppia di vertici di \(G\) è connessa. Altrimenti si dice disconnesso.
La relazione di connessione fra coppie di vertici è una relazione di equivalenza (riflessiva, simmetrica e transitiva) che induce una partizione dell’insieme dei nodi in classi di equivalenza, chiamate anche componenti connesse. Ogni classe contiene tutti e soli i vertici tra loro connessi. Naturalmente se un grafo è connesso allora esiste una sola classe di equivalenza.
Esercizio 3.1
Dimostrare che un grafo connesso con \(n\) vertici ha almeno \(n-1\) archi.
La nozione di connessione è importante per valutare la robustezza di una rete. Una rete robusta mantiene la connettività anche se un nodo viene eliminato. Ad esempio la rete internet può essere rappresentata come un enorme grafo i cui nodi sono i router e gli archi sono le linee di comunicazione. Una rete robusta deve essere progettata in modo da mantenere la connettività anche se uno o più nodi, per qualsiasi motivo, non sono più funzionanti.
Il diametro di un grafo connesso è la massima distanza fra tutte le coppie di nodi. Se il grafo non è connesso allora si dice che il grafo ha diametro infinito.
In generale per un grafo connesso con \(n\) nodi e \(m\) archi vale la relazione
3.2) Alberi
Un albero è un grafo connesso aciclico, cioè senza cicli. Un grafo privo di cicli (ma non necessariamente connesso) si chiama una foresta. Una foresta è quindi costituita da una o più componenti connesse, ognuna delle quali è un albero.
Teorema 3.1
Sia \(G=(V,E)\) un grafo connesso. Allora \(G\) è un albero se e solo se
Dimostrazione
Dimostrare per induzione, supponendo prima \(|V|=1\) e poi \(|V| \gt 1\).
Si può dimostrare che ogni grafo connesso contiene un albero generatore (spanning tree), cioè un albero che contiene tutti i vertici del grafo. L’abero generatore ha ordine \(n\) e dimensione \(n-1\).
Esercizio 3.2
Dimostrare che un albero di ordine maggiore od uguale a \(2\) contiene almeno due vertici con grado uguale ad \(1\).
4) Isomorfismo tra grafi
Descriviamo ora le condizioni per le quali due grafi, in apparenza diversi, in realtà sono equivalenti dal punto di vista strutturale.
Due grafi \(G,H\) si dicono isomorfi se esiste una corrispondenza biunivoca
tale che per ogni coppia di vertici \(x,y \in G\) si ha
\[ (x,y) \in E(G) \iff (f(x),f(y)) \in E(H) \]Nel caso di grafi isomorfi la funzione \(f\) preserva la proprietà di adiacenza dei vertici. Infatti l’isomorfismo manda vertici adiacenti in un grafo in vertici adiacenti nell’altro grafo. In termini semplici possiamo dire che due grafi isomorfi sono uguali, a meno di una permutazione dei nomi attribuiti ai nodi.
Esempio 4.1
I due grafi seguenti sono isomorfi.
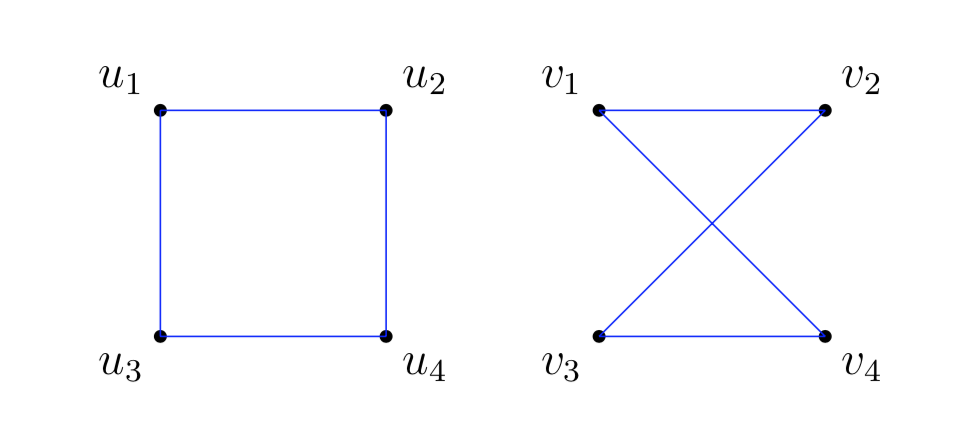
Una funzione possibile è la seguente:
\[ f(u_{1})=v_{1} \ , \quad f(u_{2})=v_{2} \ , \quad f(u_{3})=v_{4} \ , \quad f(u_{4})=v_{3} \]Se due grafi \(G,H\) sono isomorfi scriviamo \(G \sim H\). La relazione di isomorfismo è una relazione di equivalenza. Chiaramente se \(G \sim H\) allora \(|V(G)|=|V(H)|\) e \(|E(G)|=|E(H)|\). Tuttavia queste condizioni non sono sufficienti.
Due grafi isomorfi hanno la stessa sequenza di gradi dei vertici. Tuttavia non è vero il viceversa. Ad esempio i due grafi seguenti
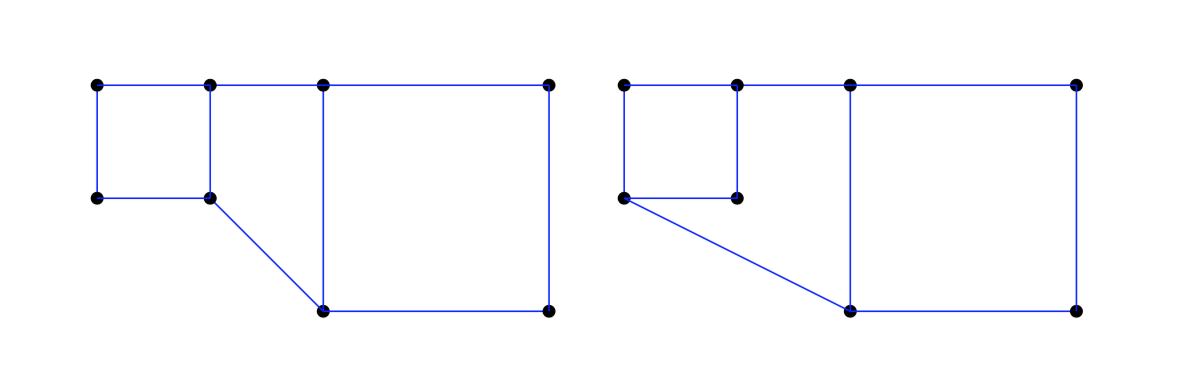
non sono isomorfi, ma hanno la stessa sequenza dei gradi dei vertici \((2, 2, 2, 2, 3, 3, 3, 3)\).
Riassumendo, due grafi isomorfi hanno alcune proprietà simili:
- il numero dei vertici e degli archi è uguale
- la sequenza dei gradi dei vertici è uguale
- il numero delle componenti connesse è uguale
Il problema di determinare se due grafi sono isomorfi è importante e difficile. Non esiste un criterio semplice di sufficienza. Una volta verificate le condizioni necessarie sul numero dei vertici e degli archi e sulla sequenza dei gradi dei vertici, è necessario applicare degli algoritmi di ricerca delle eventuali corrispondenze biunivoche fra i vertici, che rispettino la relazione di adiacenza. Non esiste un algoritmo efficiente e nel caso di grafi con un grande numero di vertici il problema può non essere risolvibile neanche con i computer più potenti.
5) Grafi orientati
Un grafo \(G=(V,E)\) si dice orientato se gli archi sono considerati come coppie ordinate, cioè \((u,v) \neq (v,u)\). Se \(e=(u,v) \in E(g)\) è un arco del grafo orientato \(G\), diremo che l’arco è uscente da \(u\) ed è entrante in \(v\). In questo caso per ogni vertice \(v\) possiamo distinguere il grado entrante e il grado uscente: il primo è dato dal numero degli archi entranti in \(v\), mentre il secondo è dato dal numero degli archi uscenti. Nella rappresentazione grafica la direzione di una un arco viene indicata con una freccia.
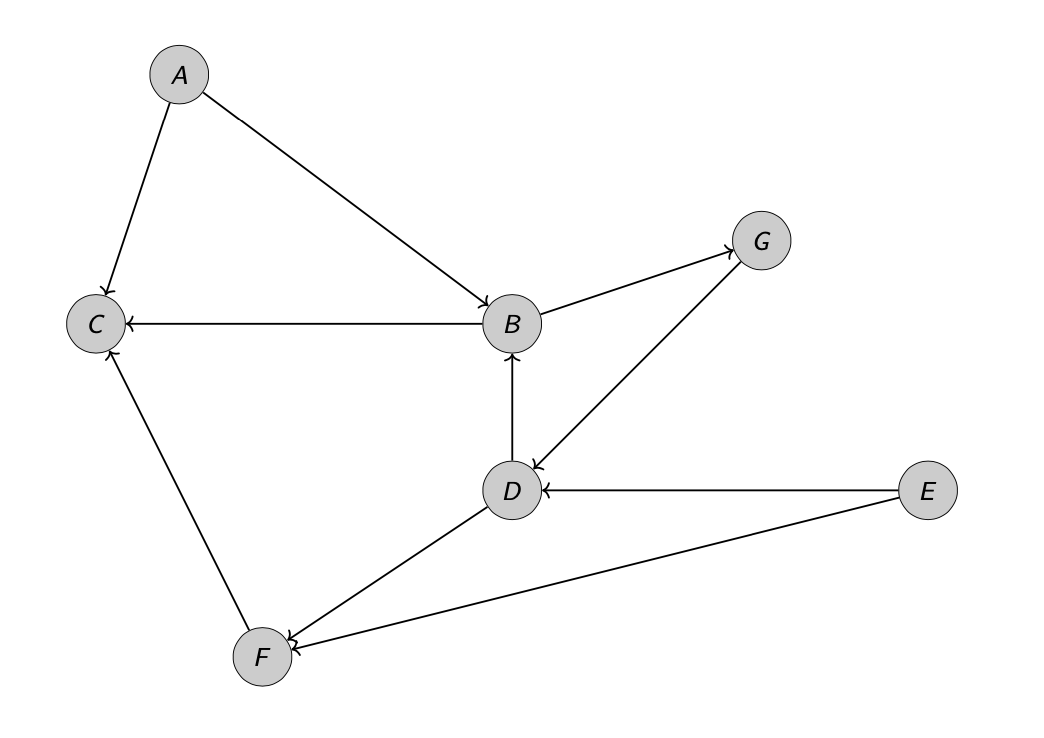
I grafi orientati sono utili per modellare sistemi con relazioni asimmetriche, in cui è necessario specificare la direzione dell’arco che collega due nodi. Ad esempio per analizzare circuiti elettrici, rappresentare le varie fasi e attività di un progetto complesso, oppure calcolare il cammino stradale più breve fra due luoghi.
Ai grafi orientati si estendono in modo naturale i concetti di intorno di un vertice, cammino, passeggiata, percorso e connettività.
Ad esempio, dato un grafo orientato \(G=(V,E)\), possiamo definire l’intorno di input \(N_{in}(u)\) e l’intorno di output \(N_{out}(u)\) di un vertice \(u \in V(G)\) in questo modo:
Esercizio 5.1
Sia dato un grafo orientato \(G=(V,E)\). Allora la somma dei gradi di input e la somma dei gradi di output sono uguali al numero totale degli archi:
Se non specificato diversamente, di seguito con il termine grafo intenderemo un grafo semplice non orientato.
6) Grafi euleriani e il problema dei sette ponti di Königsberg
La nascita della teoria dei grafi può essere fatta risalire al \(1736\), quando Eulero presentò un articolo in cui risolse il problema dei sette ponti di Königsberg, una cittadina della Prussia (oggi si chiama Kaliningrad e si trova in Russia). La città è attraversata dal fiume Pregel, che la divide in quattro zone: due zone principali all’esterno del fiume e due isole. Le quattro zone della città sono collegate tra loro da sette ponti.
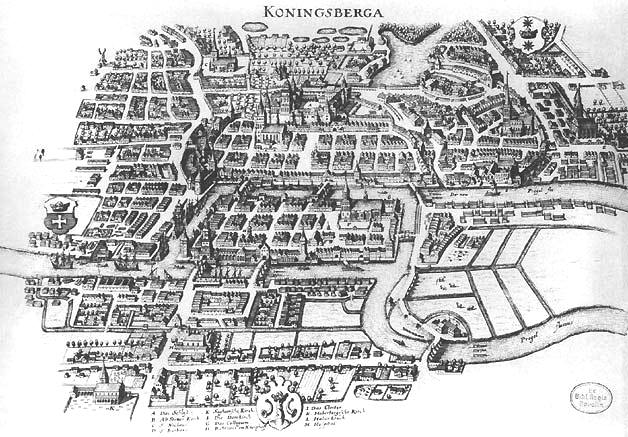
Il problema posto da Eulero è il seguente: è possibile per una persona fare una passeggiata che parta da un punto qualsiasi della città e attraversare una ed una sola volta ciascuno dei sette ponti?
Per risolvere il problema di Eulero introduciamo alcune definizioni.
Definizione 6.1
Sia dato un multigrafo \(G = (V, E)\), con \(E(G)=\{e_{0},e_{1},\cdots e_{n}\}\). Si chiama cammino euleriano in \(G\) una passeggiata \(v_{0}e_{0}v_{1}e_{1} \cdots e_{n}v_{n}\) , che passa per tutti gli archi di \(G\) una e una sola volta.
Un cammino euleriano chiuso, in cui i vertici iniziale e finale coincidono, viene detto circuito di Eulero o ciclo euleriano.
Un multigrafo connesso \(G\) è detto euleriano se ammette un circuito di Eulero.
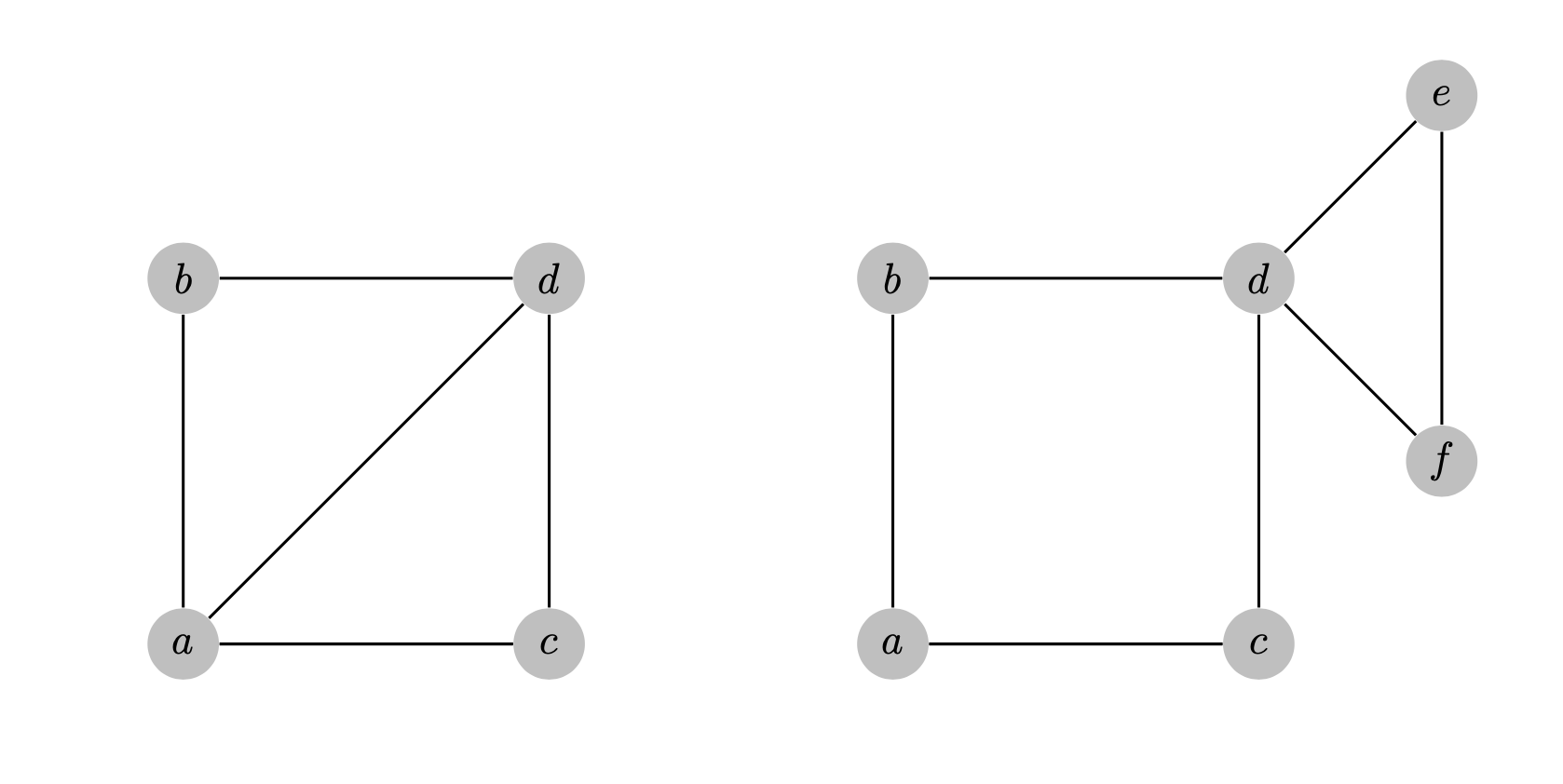
Esercizio 6.1
Trovare due cammini di Eulero in ognuno dei seguenti grafi:
Il seguente teorema di Eulero descrive la condizione necessaria e sufficiente affinché un grafo sia euleriano:
Teorema 6.1 – Eulero
Un multigrafo connesso ha un circuito di Eulero se e solo se ogni vertice ha grado pari.
Un multigrafo connesso ha un cammino di Eulero da un vertice \(u\) ad un vertice \(v\), con \(u \neq v\), se e solo se \(u,v\) sono i soli vertici di grado dispari.
Per una dimostrazione vedere [2].
La soluzione del problema dei sette ponti
Per risolvere il problema Eulero rappresentò la configurazione dei sette ponti mediante una struttura grafica, simile a quella della figura sottostante.
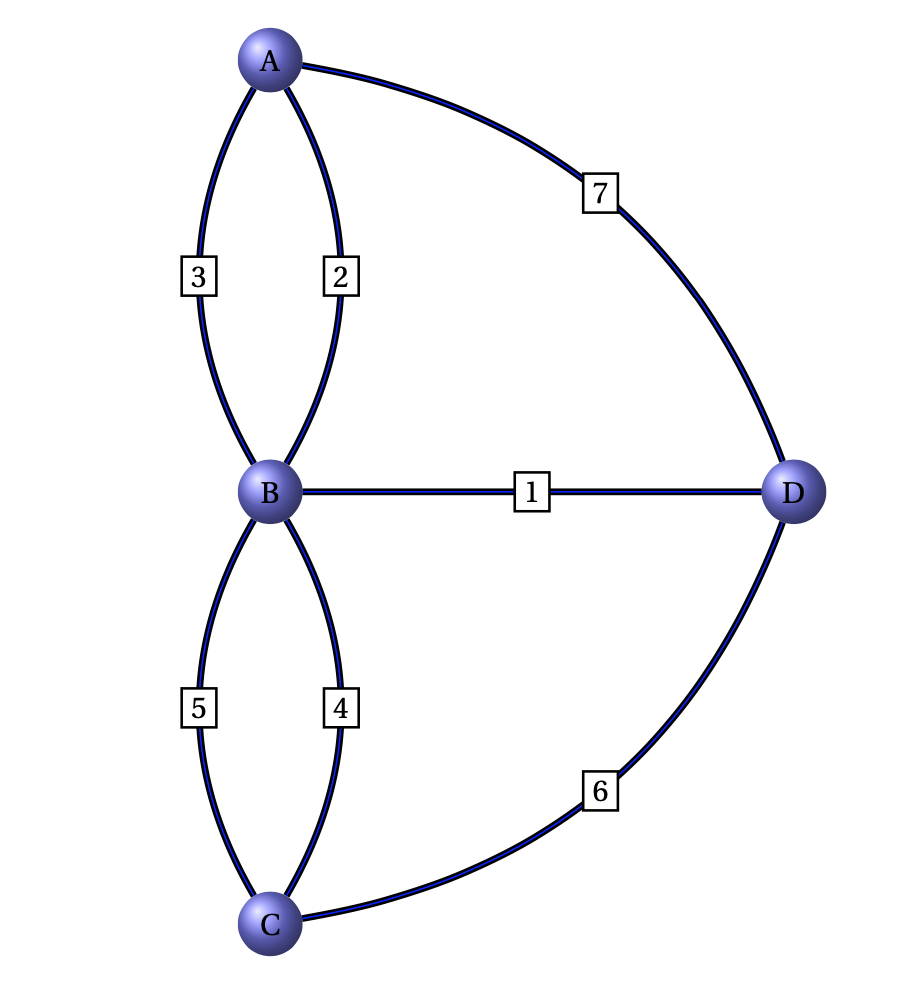
I vertici \(A,B,C,D\) rappresentano le \(4\) zone collegate dai \(7\) ponti, indicati con i numeri \(1,2,\cdots,7\).
Il problema dei ponti di Königsberg si può ridurre alla dimostrazione dell’esistenza di un circuito euleriano nel multigrafo in figura.
In base al teorema di Eulero un multigrafo connesso ha un circuito di Eulero se e solo se ogni vertice ha grado pari. Quindi il problema dei sette ponti non ammette soluzione positiva.
Stabilire se un grafo è euleriano è quindi una cosa immediata: basta guardare il grado dei vari nodi. Tuttavia, tranne nei grafi più semplici, non è in genere facile trovare cammini o circuiti euleriani. Un algoritmo utile è stato trovato dal matematico tedesco Carl Hierholzer (1840-1871). Per i dettagli vedere [3].
7) Grafi casuali
Il concetto di grafo casuale può essere definito in uno spazio di probabilità in cui ogni punto dello spazio corrisponde ad un grafo. I vari spazi di probabilità consistono di grafi su un insieme finito di vertici \(V=\{1,2,\cdots,n\}\). Supponiamo che \(X\) sia l’insieme di tutti i possibili grafi semplici non orientati con \(n\) nodi. Ogni arco fra due nodi può essere presente oppure non presente. Il numero massimo di archi è
\[ N=\displaystyle\binom{n}{2}=\dfrac{n(n-1)}{2} \]Fissato un numero \(m\) tale che \(1 \le m \le N\) di archi, il numero di grafi con \(m\) archi è \(\binom{N}{m}\). Il numero dei sottografi distinti è quindi \(2^{N}\), poiché per il teorema binomiale di Newton
\[ \binom{N}{0}+ \binom{N}{1}+\cdots + \binom{N}{N} =(1+1)^{N}=2^{N} \]Il procedimento per creare un grafo casuale semplice e connesso con \(n\) vertici consiste nel fissare, per ogni coppia di nodi \(u,v\), la probabilità \(p_{uv}\) che sia presente l’arco \((u,v)\).
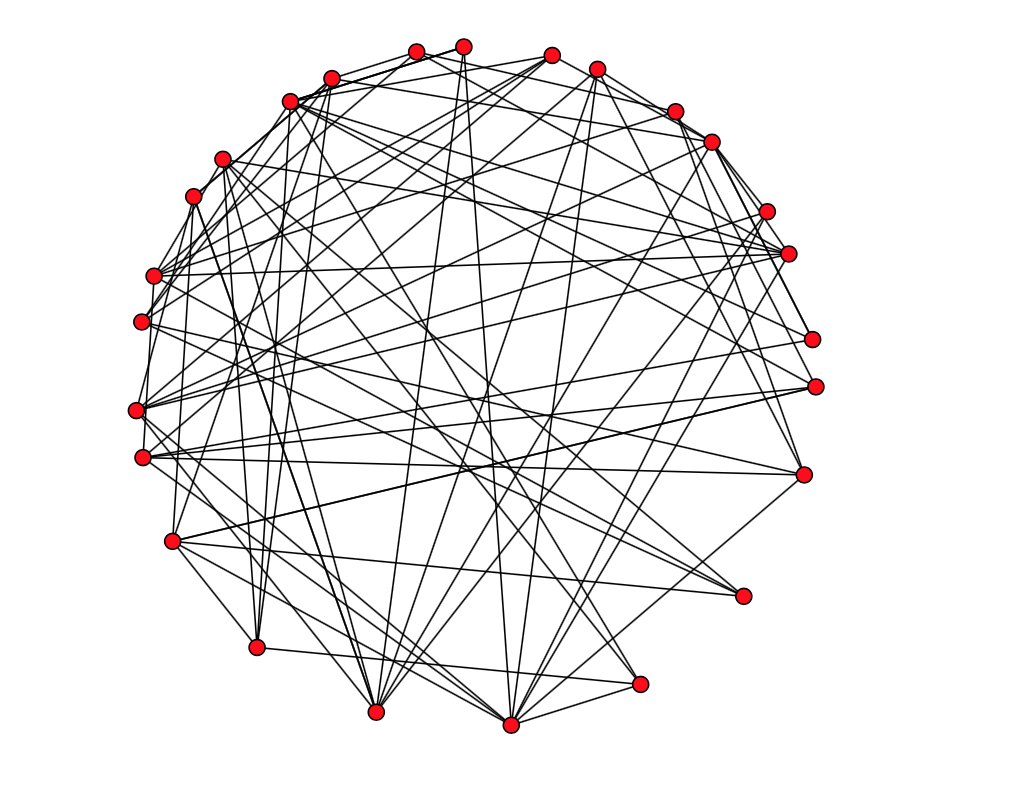
7.1) Il modello di Erdös-Rényi
Nel \(1959\) Erdös e Rényi introdussero due diversi tipi di grafi casuali: il modello uniforme e il modello binomiale.
Modello uniforme \(G(n,m)\)
Questo modello ha due parametri: il numero dei vertici \(n\) e il numero dei lati \(m\), con \(0 \le m \le \displaystyle\binom{n}{2}\).
Indichiamo con \(\mathcal{G}\) la famiglia di tutti i grafi semplici non orientati con \(n\) vertici. Abbiamo \(|\mathcal{G}|=2^{N}\), dove \(N=\displaystyle\binom{n}{2}=\dfrac{n(n-1)}{2}\). Consideriamo un grafo \(G \in \mathcal{G}\). Il modello uniforme assegna la stessa probabilità a tutti i grafi con \(m\) archi. Quindi
Modello binomiale \(G(n,p)\)
Il modello \(G(n,p)\) ha due parametri: il numero dei vertici \(n\) e una probabilità \(p,\ 0 \le p \le 1\). Il parametro \(p\) indica la probabilità che sia presente un arco fra due vertici \((u,v)\) del grafo.
Indichiamo con \(\mathcal{G}\) la famiglia di tutti i grafi semplici non orientati con \(n\) vertici. Supponiamo che la presenza di un arco sia indipendente dalla presenza degli altri archi. Consideriamo un grafo \(G \in \mathcal{G}\), con \(m=|E(G)|\). La probabilità assegnata a questo grafo è
Se \(p=0\), allora \(G(n,0)\) è un grafo vuoto con \(n\) vertici tutti isolati. Se \(p=1\), allora \(G(n,1)\) è un grafo completo \(K_{n}\).
Indichiamo con \(X\) la variabile aleatoria relativa al numero di archi presenti in un grafo \(G(n,p)\). E’ una variabile aleatoria con la distribuzione binomiale \(B(N,p)\):
dove \(N=\displaystyle\binom{n}{2}\). Il valore medio del numero degli archi nel grafo \(G(n,p)\) è quindi uguale a \(E(X)=\displaystyle\binom{n}{2}p\).
Esercizio 7.1
Indichiamo con \(Y\) la variabile aleatoria che rappresenta il numero degli archi incidenti su un fissato vertice \(v\) del grafo \(G(n,p)\). Determinare il valore atteso di \(Y\).
Soluzione
La distribuzione della variabile \(Y\) è la seguente:
Quindi il valore atteso \(E(Y)\) del numero degli archi che incidono su \(v\) è \(E(Y)=(n-1)p\).
Esercizio 7.2
Calcolare la probabilità che un fissato vertice \(v\) del grafo \(G(n,p)\) sia isolato.
Risposta: \((1-p)^{n-1}\).
Nonostante la sua semplicità, il grafo casuale \(G(n,p)\) presenta delle proprietà che sono utili anche per studiare modelli di grafi reali complessi. Molte proprietà vengono studiate asintoticamente, cioè per valori grandi di \(n\).
Alcune proprietà del grafo \(G(n,p)\)
Ricordiamo che una variabile aleatoria discreta \(X\) ha una distribuzione di Poisson se
dove \(\lambda\) è un numero reale positivo.
Come è noto la distribuzione di Poisson è una buona approssimazione della distribuzione binomiale \(B(n,p)\), al crescere del numero \(n\) delle prove, se la probabilità \(p\) di successo è piccola. Come parametro si prende \(\lambda = np\):
Riprendendo l’esercizio 7.1, per valori grandi di \(n\) la distribuzione del grado di un fissato vertice può essere approssimata in questo modo:
\[ \begin{array}{l} \displaystyle P(Y=k)= \binom{n-1}{k}p^{k}(1-p)^{n-k-1} \approx e^{-\lambda }\frac{\lambda^{k}}{k!} \\ \end{array} \]7.2) Evoluzione del grafo \(G(n,p)\)
Un modo per simulare l’evoluzione di un grafo casuale è il seguente. Fissiamo gli \(n\) vertici \(v_{1},v_{2},\cdots,v_{n}\). Quindi scegliamo in modo casuale un arco fra i possibili \(\displaystyle\binom{n}{2}\), in modo che tutti gli archi abbiano la stessa probabilità. Quindi scegliamo di nuovo a caso uno dei rimanenti archi \(\displaystyle\binom{n}{2}-1\), e così via. In questo modo abbiamo creato una successione di grafi
\[ G_{0} \subset G_{1} \subset G_{2} \cdots \subset G_{N} \ , \quad N = \binom{n}{2} \]Il grafo \(G_{k}\) contiene \(k\) archi. Chiaramente sono possibili \(N!\) diversi processi di evoluzione dal grafo \(G_{0}\) al grafo completo \(G_{N}\). L’insieme di tutti questi processi costituisce uno spazio di probabilità uniforme.
Erdös and Rényi hanno dimostrato che molte proprietà appaiono in modo discontinuo (transizioni di fase) al variare dei parametri del modello. In termini matematici, esistono delle funzioni \(k_{1}(n),k_{2}(n)\) vicine tra loro tali che quasi nessun grafo \(G_{k_{1}(n)}\) ha certe proprietà, mentre quasi tutti i grafi \(G_{k_{2}(n)}\) hanno quelle stesse proprietà.
Proprietà di connessione
Il seguente teorema illustra una proprietà fondamentale del grafo \(G(n,p)\), al crescere del numero dei nodi.
Teorema 7.1 – Erdos-Rényi
Supponiamo
Allora
\[ \begin{array}{l} \lambda \lt 1 \implies \text{P(G(n,p(n)) è connesso)} \to 0 \\ \lambda \gt 1 \implies \text{P(G(n,p(n)) è connesso)} \to 1 \end{array} \]Per la dimostrazione del teorema di Erdös-Rényi e per approfondire l’argomento dei grafi casuali vedere il testo di Bollobás.
8) Il grafo del web
Il Web (World Wide Web) è un servizio basato sulla piattaforma Internet, sviluppato per permettere la condivisioni di informazioni sulla rete. Non si deve confondere il Web con Internet, anche se i due termini spesso vengono utilizzati come sinonimi. Il termine Internet si riferisce alla infrastruttura fisica della rete globale dei server, sui quali sono residenti i vari siti web.
La nascita del web risale al \(1989\) ed è dovuta a Tim Berners-Lee, uno scienziato che lavorava al CERN di Ginevra. Lo scopo iniziale era quello di creare un sistema per condividere le informazioni fra i vari ricercatori.
Tim Berners-Lee è anche l’ideatore del concetto di URL, del protocollo HTTP per il trasferimento degli ipertesti e del linguaggio HTML. Tim Berners-Lee realizzò quindi il primo web server sul quale erano memorizzati vari documenti. I ricercatori potevano accedere ai documenti dalle loro postazioni, collegate in rete al server, mediante un programma di interfaccia, il web browser.

Oggi il Web è una rete mondiale costituita da un grande numero di siti web. Un sito web è identificato da un nome unico (ad esempio www.ibm.com) e contiene una collezione di documenti. Ogni sito web è ospitato su un server, dal punto di vista hardware, e da un web server dal punto di vista applicativo. Il web server è un’applicazione software che viene eseguita sul server e gestisce le richieste di accesso e trasferimento delle pagine fatte dal client, tramite un web browser.
Dal punto di vista applicativo possiamo definire il Web come una collezione di documenti ipertestuali. I documenti sono memorizzati su archivi residenti nei milioni di siti sparsi per il mondo. I documenti vengono resi disponibili agli utenti attraverso un protocollo client/server. Ciascun documento è identificato da un URL (Universal Resource Locator).
L’HTML (HyperText Markup Language) è un linguaggio per la preparazione dei documenti ipertestuali. Ogni documento può contenere dei collegamenti (link) ad altri documenti presenti nel sito locale o in altri siti presenti sulla rete internet.
L’Hypertext Transfer Protocol (HTTP) è il protocollo standard per il trasferimento delle pagine ipertestuali e dei contenuti multimediali nel Web.
Si può pensare all’insieme dei documenti presenti sul Web come a un grafo orientato, con le seguenti proprietà:
- i nodi sono gli URL delle pagine;
- fra due nodi \(x,y\) esiste un arco se la pagina \(x\) contiene un hyperlink verso la pagina \(y\).
Questo grafo è chiamato grafo del Web. Un hyperlink dalla pagina \(x\) alla pagina \(y\) viene rappresentato con un arco. Si tratta ovviamente di un grafo orientato e quindi, per ogni nodo, bisogna distinguere gli archi in input e gli archi in output.
Ovviamente, si tratta di un grafo altamente dinamico, che cambia in continuazione, in quanto milioni di nuove pagine e collegamenti vengono creati ogni giorno. Le dimensioni del grafo del Web sono enormi: si stima che siano presenti oltre \(10\) miliardi di nodi.
9) Modelli grafici del web
Il modello di grafo casuale di Erdös e Rényi è stato studiato ampiamente e sono state descritte molte delle sue proprietà. Tuttavia si basa su ipotesi semplificatrici, che in genere non corrispondono alla realtà di reti complesse, come la rete web o altre reti tecnologiche, biologiche o sociali.
Vediamo alcune proprietà che caratterizzano il grafo del Web.
- Il Web è un grafo orientato, in quanto i link fra le pagine sono orientati in un’unica direzione.
- Si tratta di un grafo sparso, cioè con un numero di archi piccolo, rispetto al numero dei nodi.
- Il modello casuale di Erdös e Rényi assume un numero fisso di nodi, mentre nel grafo del web il numero dei nodi cresce continuamente.
- Fenomeno del piccolo mondo: la distanza media fra due nodi, misurata in base al numero degli archi nel cammino più breve, è piccola. La teoria del mondi piccoli è dovuta al sociologo americano Stanley Milgram, ed è applicabile in molte situazioni diverse. Ad esempio in una rete sociale, se prendiamo a caso due persone della rete, risulta che esse sono collegate da un piccolo numero di conoscenze intermedie.
- Clustering: due nodi che hanno un altro nodo in comune, tendono ad essere connessi essi stessi. Questa proprietà viene misurata mediante un parametro chiamato coefficiente di clustering. Nelle reti casuali questo fenomeno non si verifica, in quanto ogni nodo ha la stessa probabilità di essere connesso ad ognuno degli atri nodi.
- Collegamento preferenziale: i nuovi collegamenti tendono a collegare i nodi maggiormente connessi, diversamente dai grafi casuali.
9.1) Legge di potenza della distribuzione dei gradi
Ricordiamo che una rete si dice ad invarianza di scala (scale free network) se la distribuzione dei gradi dei nodi della rete segue una legge di potenza. In termini semplici significa che la maggioranza dei nodi ha pochi collegamenti, mentre alcuni nodi importanti (chiamati anche hub) hanno un numero elevato di collegamenti.
Formalmente la legge di potenza implica che la probabilità \(P(k)\) che un nodo abbia grado uguale a \(k\) è la seguente:
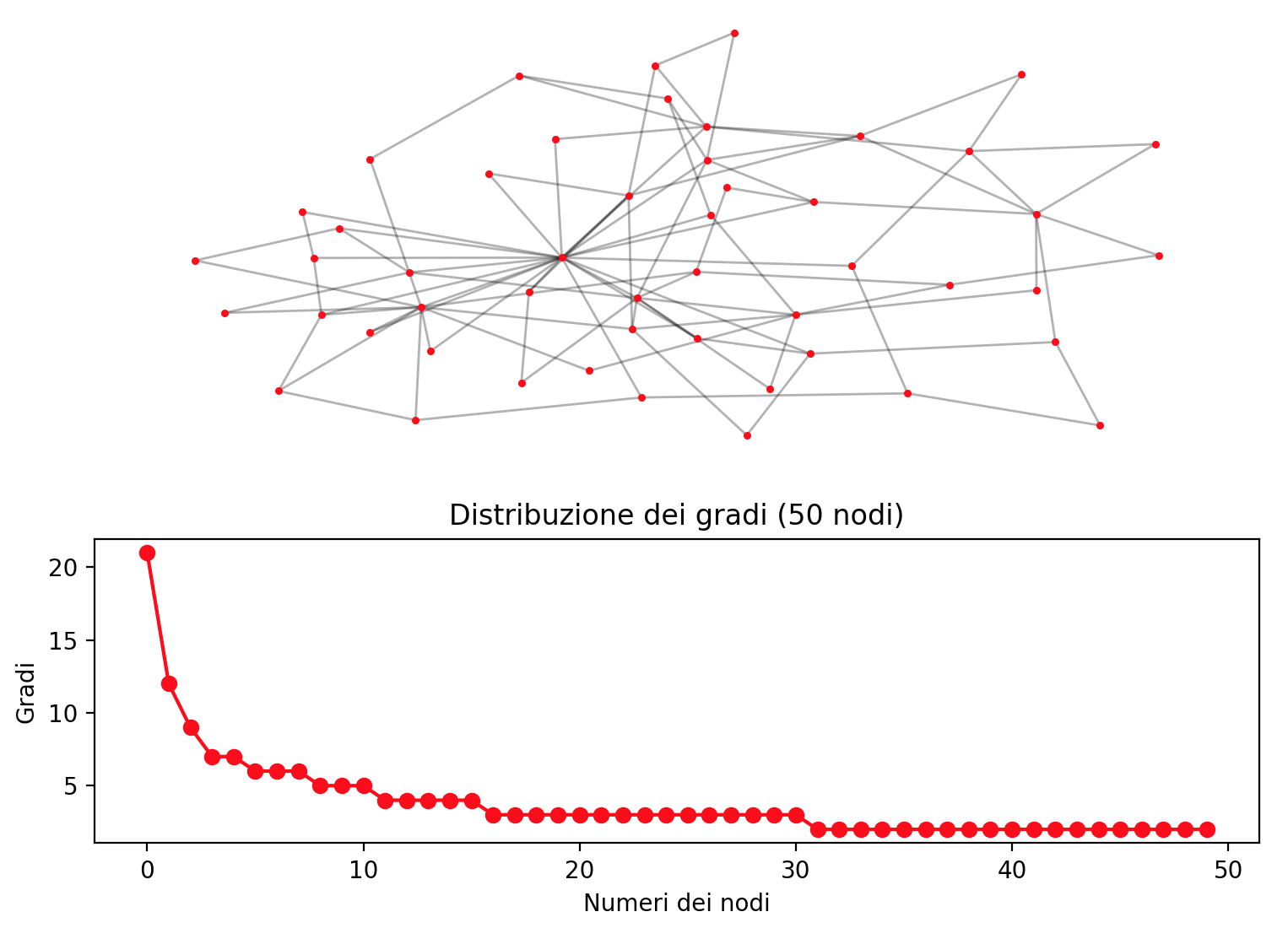
All’aumentare del valore di \(k\) rimane significativa la probabilità di trovare un nodo con un grado elevato. La presenta di questi nodi connettori è caratteristica delle reti che seguono una legge di potenza.
Per studiare il fenomeno si può utilizzare un diagramma cartesiano, mettendo nell’asse delle ascisse valori di \(k\) e nell’ordinata la frazione percentuale dei nodi. La maggior parte dei nodi ha un grado basso; tuttavia un certo numero piccolo di nodi ha un grado molto elevato, soprattutto nelle reti complesse, con diverse migliaia di nodi. Per riconoscere questo fenomeno è meglio utilizzare una scala logaritmica.
Il nome invarianza di scala deriva dal fatto che la legge di potenza rimane invariata, tranne che per un fattore moltiplicativo, se si cambia scala alla variabile indipendente \(k\):
Gli studi effettuati su molte reti complesse reali di vario tipo (sociale, tecnologico, biologico, ecc.) hanno mostrato che, per valori molto grandi del numero dei nodi, i gradi dei nodi hanno una distribuzione \(P(k)\) che soddisfa la legge di potenza.
9.2) Il modello Barabási-Albert
Per simulare il comportamento delle reti complesse, come la rete web, sono stati proposti diversi modelli teorici. Uno dei più noti è il modello basato sul collegamento preferenziale, noto come modello \(BA\), proposto da Barabási-Albert nel \(1999\).
Il modello si basa su due ipotesi fondamentali:
- crescita ed espansione continua del grafo: a partire da un grafo iniziale il numero dei nodi aumenta di una nuova unità in ogni ciclo temporale;
- collegamento preferenziale: ogni volta che si aggiunge un nuovo collegamento, è più probabile che questo si connetta ad un nodo che ha già un alto numero di collegamenti.
L’algoritmo del modello Barabási-Albert ha tre parametri di input:
- \(n_{0}\) – numero di nodi del grafo iniziale
- \(m\) – numero di archi da aggiungere ad ogni nuovo nodo
- \(n\) – numero di nodi del grafo finale, che determina la fine dell’algoritmo
Nella fase iniziale viene creato un piccolo grafo \(G_{0}\), costituito da \(n_{0}\) nodi. Il grafo iniziale deve essere connesso, quindi ogni nodo ha almeno un collegamento.
Il ciclo dell’algoritmo è costituiti da due fasi principali:
- fase A – Aggiunta di un nodo
Aggiungiamo un nuovo nodo \(v_{t+1}\) per creare il grafo \(G_{t+1}\) a partire dal grafo \(G_{t}\), con \(t=0,1,2,\cdots\). - fase B – Aggiunta di collegamenti al nuovo nodo
Quindi colleghiamo questo nodo con \(m \le n_{0}\) collegamenti con altrettanti nodi del grafo \(G_{t}\). Per la scelta dei nodi da collegare utilizziamo il criterio del collegamento preferenziale.
Per applicare la regola del collegamento preferenziale si applica il seguente criterio. Aggiungiamo un nuovo vertice \(v_{t+1}\) al grafo \(G_{t}\) per creare il grafo \(G_{t+1}\). Quindi colleghiamo il nuovo nodo \(v_{t+1}\) con \(m\) nodi del grafo. La probabilità \(P(t+1,i)\) che il nuovo nodo \(v_{t+1}\) si connetta con un nodo \( v_{i} \), con grado \(\deg(v_{i})\), è la seguente:
\[ P(t+1,i)= \frac{\deg(v_{i})}{\sum_{v \in G_{t}} deg(v)} \]L’algoritmo viene terminato dopo aver creato un grafo con \(n\) nodi. Il grafo risultante viene chiamato grafo \(BA(n_{0},m,n)\).
9.3) Evoluzione del modello Barabási-Albert
Dopo \(k\) cicli il grafo avrà \(n_{0}+k\) nodi e \(m\cdot k + |E(G_{0}|\) archi. In base alla regola del collegamento preferenziale i nodi più grandi acquisiranno ulteriori collegamenti, a spese dei nodi più piccoli.
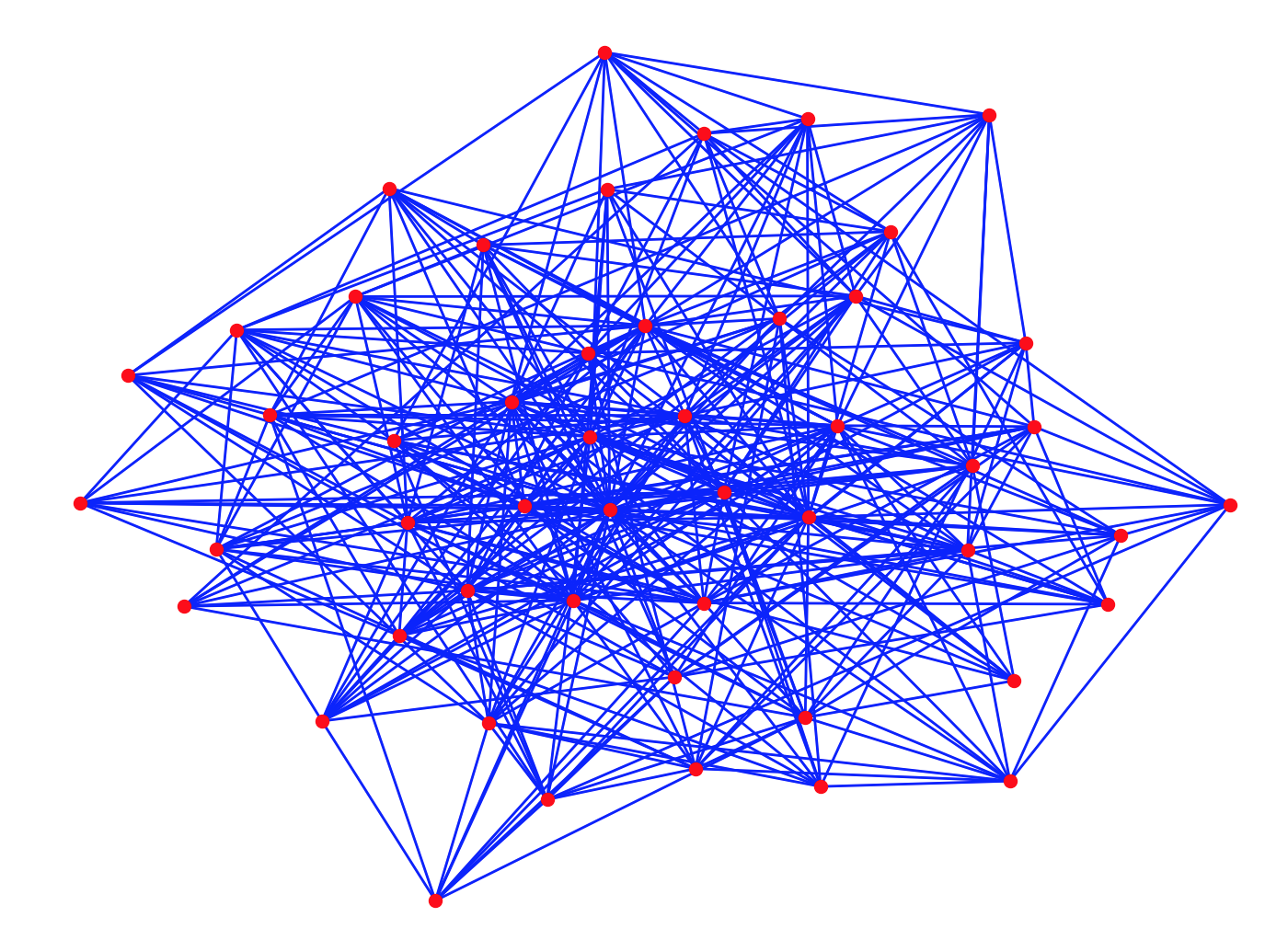
Si può dimostrare che questo modello verifica la legge di potenza. In particolare Barabási e Albert hanno dimostrato che in questo modello la probabilità \(P(k)\) che un vertice arbitrario \(v\) abbia grado uguale a \(k\) è proporzionale a \(k^{-3}\).
La dimostrazione è piuttosto lunga e complessa. Per i dettagli vedere il testo di Bonato [4]. Nello stesso testo sono descritti anche altri modelli, di maggiore complessità, proposti da vari studiosi per simulare proprietà del grafo del Web.
Conclusione
La teoria dei grafi, nata con il problema di Eulero dei sette ponti di Königsberg, è ormai diventata un ramo importante della matematica e ha trovato applicazione in molti settori delle scienza e della tecnologia. Ad esempio è utilizzata in biologia molecolare, ingegneria elettrica, scienza dell’informazione, ricerca operativa, ecc.
Il grafo del Web ha ormai raggiunto dimensioni enormi ed è in continua crescita. Lo studio di questo grafo rappresenta una grande sfida dal punto di vista matematico.
In un prossimo articolo studieremo il funzionamento dei motori di ricerca, come Google, i quali utilizzano le varie rappresentazioni del grafo del web per ricercare e classificare le informazioni presenti nelle varie pagine.
Bibliografia
[1]T. Cormen – Introduction to Algorithms (The MIT Press)
[2]Béla Bollobás – Modern Graph Theory (Springer)
[3]John M. Harris, Jeffry L. Hirst, Michael J. Mossinghoff – Combinatorics and Graph Theory (Springer)
[4]A. Bonato – A Course on the Web Graph (American Mathematical Society)
[5]F. Menczer, S. Fortunato, C. Davis – A First Course in Network Science (Cambridge U.P.)
0 commenti