Teoria dell’Informazione (II) – I Canali di Informazione

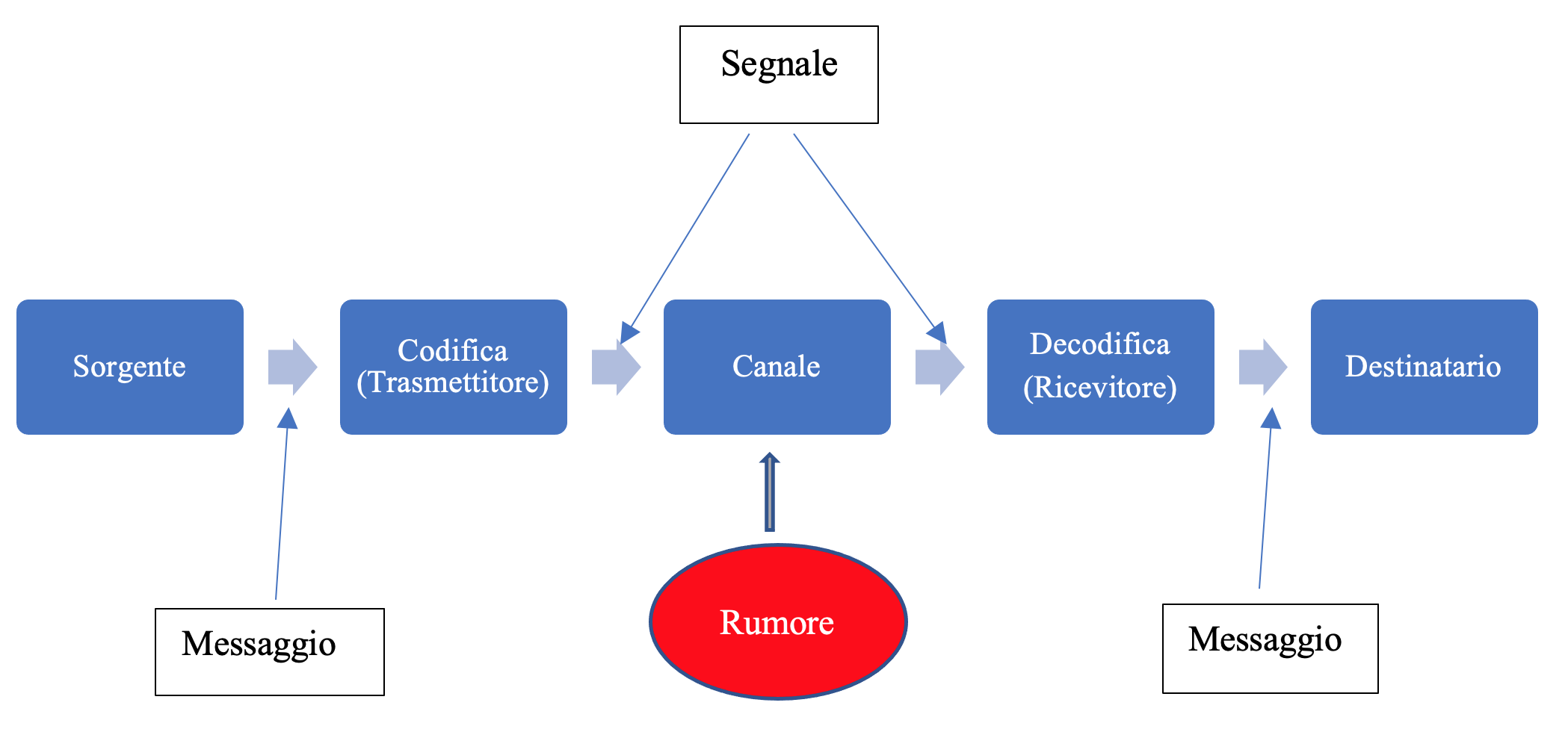
In un articolo precedente abbiamo esaminato il problema della trasmissione di messaggi in presenza di un canale ideale privo di rumore e quindi senza errori. Abbiamo studiato il primo teorema di Shannon che permette di individuare i codici ottimali per la sorgente.
In questo articolo studieremo la trasmissione di un messaggio attraverso un canale in cui è presente il rumore. La presenza del rumore può modificare il messaggio di input, e quindi il messaggio che arriva al destinatario può essere diverso da quello trasmesso dalla sorgente. È importante quindi poter misurare la quantità di informazione che viene trasmessa e quella che viene persa in questo contesto.

---

1) Il canale di trasmissione

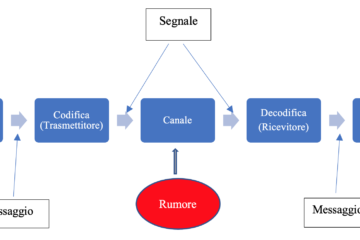
Ricordiamo il modello di Shannon-Weaver per un sistema di trasmissione:

Un canale di trasmissione discreto è costituito dai seguenti componenti:

• un alfabeto di input
• un alfabeto di output
• una matrice di probabilità condizionate

Sia $A$ un alfabeto finito di simboli $A=\{a_{1},a_{2},\cdots,a_{r}\}$, con una data distribuzione di probabilità

$$p_{k}=P(a_{k}) \quad k=1,2,\cdots,r$$

I simboli dell’alfabeto $A$ vengono dati in input al canale, attraverso il quale vengono trasmessi e raggiungono il punto finale di output.
A causa del rumore i simboli che arrivano al punto di destinazione possono essere diversi e quindi appartenere ad un altro alfabeto $B=\{b_{1},b_{2}, \cdots, b_{s}\}$ con distribuzione di probabilità

$$q_{k}=P(b_{k}) \quad k=1,2,\cdots,s$$

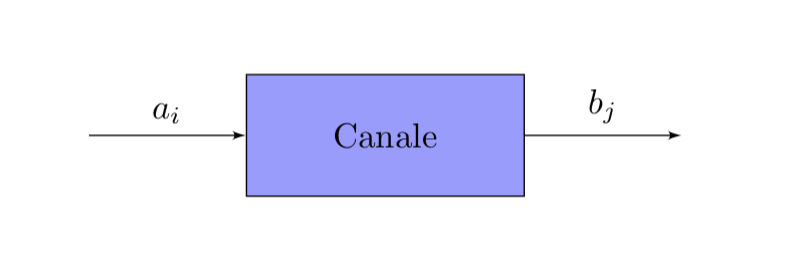
Indichiamo il canale con la notazione $K=(A,B)$. Gli insiemi $A,B$ possono essere diversi oppure uguali. Anche se fossero uguali, questo non significa che ogni singolo simbolo $a_{k}$ venga trasmesso in modo corretto.
Il canale si dice senza memoria se la distribuzione di probabilità dell’output non dipende dai precedenti simboli ricevuti. Assumiamo inoltre che le proprietà non variano nel tempo.
Per ogni coppia di indici $i \in \{1,2,\cdots,r\}$ e $j \in \{1,2,\cdots,s\}$, definiamo la probabilità condizionata che l’output sia $b_{j}$ dato che l’input trasmesso è $a_{i}$:

$$P_{ij}=P(b_{j}|a_{i})$$

Le probabilità $P_{ij}$ si chiamano probabilità di transizione o probabilità in avanti (forward probabilities).
La matrice del canale è quindi

$$\begin{pmatrix} P_{11} & P_{12} & \cdots & P_{1s} \\ P_{21} & P_{22} & \cdots & P_{2s} \\ \vdots & & \ddots & \vdots \\ P_{r1} & P_{r2} & \cdots & P_{rs} \\ \end{pmatrix}$$

Se almeno un termine della matrice che non si trova sulla diagonale principale è non nullo, allora siamo in presenza di canale con rumore. Chiaramente si ha

$$\sum\limits_{j=1}^{s}P_{ij}=1 \quad i=1,2,\cdots,r$$

Un canale discreto senza memoria è univocamente determinato dall’alfabeto di input $A$, da quello di output $B$ e dalla matrice delle probabilità di transizione $(P_{ij})$.

Esempio 1.1 – Il canale binario simmetrico
L’esempio più semplice è il canale binario simmetrico (BSC – binary symmetric channel). È un canale discreto senza memoria. Gli alfabeti di input e output sono $A=\{0,1\}$ e $B=\{0,1\}$. Il funzionamento del canale dipende da un parametro di probabilità $p_{e}$ compreso nell’intervallo $[0,1]$, che indica la probabilità di errore. Si dice simmetrico poiché la probabilità di ricevere $1$ quando si è inviato $0$ è la stessa di ricevere $0$ quando si è inviato $1$. La matrice di probabilità è la seguente:

$$\begin{pmatrix} 1-p_{e} & p_{e} \\ p_{e} & 1-p_{e} \\ \end{pmatrix}$$

Esempio 1.2 – Canale binario a cancellazione
Nel canale binario a cancellazione (BEC – binary erasure channel) i due alfabeti sono $A=\{0,1\}$ e $b=\{0,1,\xi\}$, dove $\xi$ indica un carattere ambiguo, illeggibile, che non permette di prendere una decisione sul simbolo trasmesso. I simboli dell’alfabeto $A$ vengono trasmessi correttamente con probabilità $1-p_{e}$, mentre vengono trasmessi in modo da essere illeggibili con probabilità $p_{e}$.
La matrice di probabilità è la seguente:

$$\begin{pmatrix} 1-p_{e} & 0 &p_{e} \\ 0 & 1-p_{e} & p_{e} \\ \end{pmatrix}$$

I canali BEC possono essere usati per simulare la trasmissione sulle reti dove i messaggi vengono trasmessi mediante pacchetti di bit. I pacchetti possono arrivare correttamente a destinazione o possono andare perduti per qualche motivo. Tuttavia in genere le perdite di pacchetti vicini non sono indipendenti.

Esercizio 1.1 – Il canale binario asimmetrico
Il canale binario asimmetrico differisce dal canale BSC in quanto la probabilità di errore quando viene inviato il simbolo $0$ è $p_{a}$ e la probabilità di errore quando viene inviato il simbolo $1$ è $p_{b}$, con $p_{a} \neq p_{b}$. Determinare la matrice di transizione del canale.

Definizione 1.1 – Somma di due canali
Dati due canali $K_{1}=(A_{1},B_{1})$ e $K_{2}=(A_{2},B_{2})$, se $A_{1} \cap A_{2}=\emptyset$ e $B_{1} \cap B_{2}=\emptyset$, possiamo definire la somma dei due canali $K=K_{1}+K_{2}=(A_{1}\cup A_{2},B_{1}\cup B_{2})$.

Definizione 1.2 – Prodotto di due canali
Dati due canali $K_{1}=(A_{1},B_{1})$ e $K_{2}=(A_{2},B_{2})$ possiamo definire il canale prodotto cartesiano $K=K_{1} \times K_{2}=(A_{1}\times A_{2},B_{1}\times B_{2})$.
In questo caso vengono trasmesse coppie di simboli $a_{i},a_{j}$ e vengono ricevute coppie di simboli $b_{k},b_{l}$. Assumendo l’indipendenza le probabilità di transizione sono

$$P((b_{k},b_{l})| (a_{i},a_{j}))=P(b_{k}|a_{i})\cdot P(b_{l}|a_{j})$$

Esercizio 1.2
Dati due canali simmetrici $K_{1},K_{2}$ trovare le matrici corrispondenti alla somma e al prodotto.

Definizione 1.3 – Combinazioni di due canali in serie
Dati due canali $K_{1}=(A_{1},B_{1})$ e $K_{2}=(A_{2},B_{2})$, con matrici rispettive $M_{1}$ e $M_{2}$, possiamo definire il canale risultante dalla combinazione in serie $K=K_{1} \circ K_{2}$.
Dimostrare che la matrice corrispondente è uguale al prodotto delle due matrici $M_{1},M_{2}$.
Ricordiamo che date due matrici

$$A= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} \quad B= \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{pmatrix} \quad$$

il prodotto $A \cdot B$ è la matrice $C=(c_{ij})$ dove

$$\begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \\ \end{pmatrix} = \begin{pmatrix} a_{11}b_{11}+ a_{12}b_{21} & a_{11}b_{12}+ a_{12}b_{22} \\ a_{21}b_{11}+ a_{22}b_{21} & a_{21}b_{12}+ a_{22}b_{22} \\ \end{pmatrix}$$

Conoscendo la distribuzione di probabilità dell’alfabeto di input e la matrice del canale, è possibile calcolare la distribuzione di probabilità dell’alfabeto di output:

Teorema 1.1

$$q_{k}=\sum\limits_{i=1}^{r}p_{i}P_{ik} \quad k=1,2, \cdots, s$$

Questa formula può essere scritta in forma compatta utilizzando la notazione matriciale

$$\mathbf{q}=\mathbf{p}M$$ $$\begin{pmatrix} q_{1}, q_{2}, \cdots , q_{s} \\ \end{pmatrix} = \begin{pmatrix} p_{1}, p_{2}, \cdots, p_{r} \end{pmatrix} \cdot \begin{pmatrix} P_{11} & P_{12} & \cdots & P_{1s} \\ P_{21} & P_{22} & \cdots & P_{2s} \\ \vdots & & \ddots & \vdots \\ P_{r1} & P_{r2} & \cdots & P_{rs} \\ \end{pmatrix}$$

dove $\mathbf{p}$ è un vettore dello spazio $\mathbb{R}^{r}$, mentre $\mathbf{q}$ è un vettore dello spazio $\mathbb{R}^{s}$.

Definizione 1.4
Oltre alle probabilità di transizione in avanti $P_{ij}$ possiamo definire anche le probabilità all’indietro (backward probabilities) per determinare le probabilità dei simboli trasmessi, conoscendo le probabilità dei simboli arrivati a destinazione:

$$Q_{ij}=P(a_{i}|b_{j})$$

Le probabilità all’indietro assumono il punto di vista del ricevente: dato che è arrivato il simbolo $b_{j}$ quale è la probabilità che sia stato trasmesso il simbolo $a_{i}$?
Infine possiamo definire le probabilità congiunte, riguardanti le probabilità della varie combinazioni di coppie di simboli $(a_{i},b_{k})$:

$$R_{ik}=P(a_{i},b_{k})$$

Per determinare le relazioni fra i vari tipi di probabilità ricordiamo la formula delle probabilità condizionate di Bayes. Dati due eventi $A,B$, con $P(B) \neq 0$ si ha

$$P(A|B)= \frac {P(A \land B)}{P(B)}=\frac{P(B|A)P(A)}{P(B)}$$

dove $P(A \land B)$ è la probabilità che si verifichino entrambi gli eventi $A,B$.
Dalla formula di Bayes si deriva facilmente la seguente relazione

$$q_{j}Q_{ij}=p_{i}P_{ij}$$

Mettendo insieme le precedenti equazioni si trova il seguente:

Teorema 1.1

$$Q_{ij}=\dfrac{p_{i}P_{ij}}{\sum_{k=1}^{r}p_{k}P_{kj}}$$

Esempio 1.3 – Trasmissione su un canale BSC
Siano $A=\{0,1\}$ e $B=\{0,1\}$ gli alfabeti di input e output. Indichiamo con $p_{e}$ la probabilità di errore di trasmissione.
Sia $\mathbf{p}=[p_{0},p_{1}]$ il vettore delle probabilità dei due simboli di $A$. Sia $\mathbf{q}=[q_{0},q_{1}]$ il vettore delle probabilità dei due simboli di $B$.
L’equazione matriciale diventa

$$\begin{pmatrix} q_{0}, q_{1} \\ \end{pmatrix} = \begin{pmatrix} p_{0}, p_{1} \end{pmatrix} \cdot \begin{pmatrix} 1-p_{e} & p_{e} \\ p_{e} & 1-p_{e} \\ \end{pmatrix}$$

che è equivalente al seguente sistema di equazioni

$$\begin{array}{l} q_{0} = p_{0}(1-p_{e}) + p_{1}p_{e} \\ q_{1} = p_{0}p_{e} + p_{1}(1-p_{e}) \\ \end{array}$$

---

2) Entropia condizionale

La presenza del rumore aumenta l’incertezza dell’input e dell’output di un sistema di trasmissione. Per misurare l’informazione trasmessa da un canale in presenza di rumore introduciamo il concetto di entropia condizionale.
Ricordiamo che le entropie dell’alfabeto di input $A$ e dell’alfabeto di output $B$ sono rispettivamente

$$H(A)= -\sum\limits_{k=1}^{r}p_{k}\log_{2}p_{k} \ ,\quad H(B)= -\sum\limits_{k=1}^{s}q_{k}\log_{2}q_{k}$$

Nel caso di alfabeto binario, ad esempio $A=\{0,1\}$, con le probabilità $p_{0}=p$ e $p_{1}=1-p$, abbiamo una distribuzione di Bernoulli. In questo caso l’entropia $H(A)$ può essere indicata anche con la funzione di una variabile $H(p)$:

$$H(p)= -p\log_{2}p -(1-p)\log_{2}(1-p)$$

Definizione 2.1
L’entropia condizionale di $A$, dato che si è ricevuto il simbolo $b_{k}$, è

$$H(A|b_{k})= -\sum\limits_{i=1}^{r}P(a_{i}|b_{k})\log_{2}P(a_{i}|b_{k})$$

Questa quantità misura l’incertezza sul simbolo trasmesso (ovvero il simbolo emesso dalla sorgente) una volta che è stato ricevuto il simbolo $b_{k}$.
La $H(A|b_{k})$ è una variabile aleatoria; il valore atteso o valore medio di questa variabile aleatoria, calcolato su tutti i possibili simboli in uscita, è l’entropia condizionale $H(A|B)$:

$$H(A|B)= \sum\limits_{k=1}^{s}q_{k}H(A|b_{k})$$

La $H(A|B)$ viene anche chiamata equivocazione di $A$ rispetto a $B$, e rappresenta l’incertezza sul simbolo trasmesso che resta una volta conosciuto il simbolo ricevuto. Si può anche interpretare come l’informazione che è stata persa a causa della presenza del rumore nel canale.

Esercizio 2.1
Dimostrare le seguenti formule:

$$\begin{array}{l} H(A|b_{k})=-\sum\limits_{i=1}^{r}Q_{ik}\log_{2}Q_{ik} \\ H(A|B)=-\sum\limits_{i=1}^{r}\sum\limits_{k=1}^{s} R_{ik}\log_{2}Q_{ik} \\ \end{array}$$

Formule simili valgono per l’entropia condizionale di $B$, dato che si è ricevuto il simbolo $a_{i}$ e l’equivocazione di $B$ rispetto ad $A$.

Esercizio 2.2
Dimostrare le seguenti formule:

$$\begin{array}{l} H(B|a_{i})= -\sum\limits_{k=1}^{r}P_{ik}\log_{2}P_{ik} \\ H(B|A)= -\sum\limits_{i=1}^{r}\sum\limits_{k=1}^{s} R_{ik}\log_{2}P_{ik} \\ \end{array}$$

Definizione 2.2 – Entropia congiunta
L’entropia congiunta $H(A,B)$ è così definita:.

$$\begin{array}{l} H(A,B)= -\sum\limits_{i=1}^{r}\sum\limits_{k=1}^{s} R_{ik}\log_{2}R_{ik} \\ \end{array}$$

Poiché $\sum\limits_{k=1}^{s}R_{ik}=p_{i}$ si dimostra facilmente la seguente relazione

$$H(A,B)= H(B)+ H(A|B)=H(A)+ H(B|A)$$

Se le variabili $A,B$ sono indipendenti allora

$$H(A,B)= H(A)+ H(B)$$

Esercizio 2.3
Dimostrare che per un canale BSC con probabilità di errore $p_{e}$ l’entropia condizionale $H(B|A)$ è

$$H(B|A) = H(p_{e})=-p_{e}\log_{2}p_{e}- (1-p_{e})\log_{2}(1-p_{e}) \\ $$

Esercizio 2.4
Dimostrare che per un canale BSC con probabilità di errore $p_{e}$ l’entropia condizionale $H(A|B)$ è

$$H(A|B)=H(p) -H(q) + H(p_{e})$$

Dimostrazione
Ricordiamo che che per un canale BSC abbiamo

$$\begin{array}{l} H(A)=H(p) = -p \ln p -(1-p) \ln (1-p) \\ H(B)=H(q) = -q \ln q -(1-q) \ln (1-q) \\ \end{array}$$

dove $p=p_{0}=P(a=0)$ e $q=q_{0}=P(b=0)$. L’entropia congiunta di $A$ e $B$ è

$$\begin{array}{l} H(A,B) = H(A) +H(B|A)=H(p)+H(p_{e}) \\ H(A,B) = H(B) +H(A|B)=H(q)+H(A|B) \\ \end{array}$$

Dalle precedenti relazioni, notando che $H(1-p_{e})=H(p_{e})$ si ricava

$$H(A|B) = H(p)+ H(p_{e}) – H(q)$$

---

3) Estensione Primo Teorema di Shannon

Nell’articolo precedente abbiamo dimostrato il primo teorema di Shannon sulla codifica di sorgente. È possibile dare una versione del teorema per i canali di informazione. Supponendo di aver ricevuto il simbolo $b_{k}$ si determina un codice di Shannon-Fano utilizzando le probabilità condizionali $P(a_{i}|b_{k})$ invece delle $P(a_{i})$. La lunghezza $L_{k}$ media del codice istantaneo creato soddisfa la relazione

$$H(A|b_{k}) \le L_{k} \le H(A|b_{k})+1$$

Sostanzialmente viene creato un codice $C_{k}$ per ogni simbolo di output $b_{k}$. Facendo la media su tutti i simboli di output otteniamo la seguente relazione per l’equivocazione di $A$ rispetto a $B$:

$$H(A|B) \le L \le H(A|B)+1$$

dove $L=\sum\limits_{k=1}^{s}q_{k}L_{k}$.
Se ora consideriamo le estensioni $A^{n}$ e $B^{n}$ degli alfabeti di input e output, possiamo creare un codice Shannon-Fano di $A^{n}$ di lunghezza $L_{n}$, che soddisfa la seguente relazione:

$$H(A^{n}|B^{n}) \le L_{n} \le H(A^{n}|B^{n})+1$$

Completando i passaggi abbiamo la seguente versione del Primo teorema di Shannon applicata ai canali di informazione:

Teorema 3.1
Supponiamo di conoscere l’output $B$ di un canale $K=(A,B)$. Allora codificando l’estensione $A^{n}$, con $n$ sufficientemente grande, possiamo trovare un codice univocamente decodificabile per l’input $A$ la cui lunghezza media è arbitrariamente vicina all’equivocazione $H(A|B)$.

L’equivocazione $H(A|B)$ rappresenta l’informazione aggiuntiva necessaria per eliminare l’incertezza sull’input del canale.

---

4) Informazione mutua

Definizione 4.1
L’informazione mutua media $I(A;B)$ di un canale è così definita

$$I(A;B)=H(A) -H(A|B)=H(A) -\sum\limits_{k=1}^{s}H(A|b_{k})P(b_{k})$$

Come sappiamo l’entropia $H(A)$ di una sorgente è una misura dell’incertezza sui simboli trasmessi sul canale, prima di conoscere il messaggio arrivato al destinatario. L’informazione mutua può essere interpretata in vari modi:

• misura di quanto è ridotta in media l’incertezza su $A$ conoscendo $B$;
• misura la quantità informazione relativa ad $A$ fornita da $B$;
• misura la riduzione dell’incertezza sul simbolo emesso da $A$ dopo aver osservato il simbolo ricevuto.

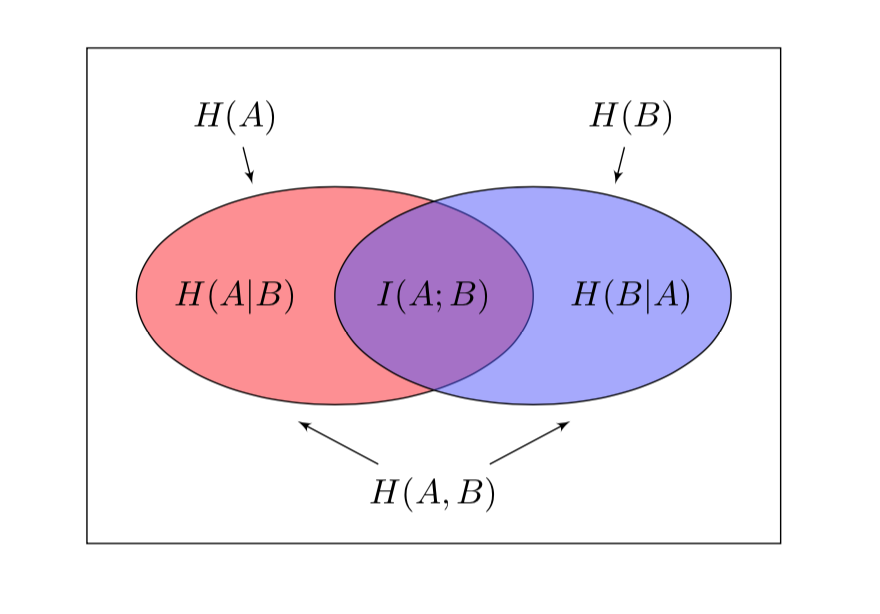
Come abbiamo visto l’informazione mutua $I(A;B)$ è una misura dell’informazione che una variabile aleatoria (in questo caso $B$) contiene rispetto ad un altra (in questo caso la $A$). Possiamo anche invertire i ruoli e definire $I(B;A)$:

$$I(B;A)=H(B) -H(B|A)$$

Esercizio 4.1
Dimostrare che $I(A;B)=I(B;A)$

Esercizio 4.2
Dimostrare che

$$I(A;B)=H(A)+ H(B) -H(A,B)$$

Esempio 4.1 – Canale BSC
Per un canale BSC l’informazione mutua è

$$I(A;B) = H(B) – H(p_{e})$$

---

5) Capacità di un canale

La capacità di un canale è una misura della massima quantità di informazione che può essere trasmessa attraverso il canale.
Come abbiamo visto l’informazione mutua $I(A;B)$ di un canale misura la quantità di informazione che viene trasmessa. Questa misura dipende da due fattori principali:

• la distribuzione di probabilità dell’alfabeto di input $A$
• le probabilità di transizione $P_{ij}$

Definizione 5.1
La capacità di un canale $K=(A,B)$ è il massimo valore dell’informazione mutua $I(A;B)$, al variare delle distribuzioni di probabilità dell’alfabeto $A$, mantenendo invariate le probabilità di transizione:

$$C = \underbrace{\max}_{p(A)} I(A;B)=\underbrace{\max}_{p(A)} H(A) -H(A|B) \quad \text{bit/simbolo}$$

La capacità di un canale è misurata in bit per simbolo. Conoscendo la durata media per la trasmissione di un simbolo, si può calcolare la capacità in termini di bit per secondo.

Esempio 5.1 – Canale binario senza errori
In questo caso si ha $P(a=0)=P(b=0)=p_{0}$ e $P(a=1)=P(b=1)=p_{1}$. L’informazione mutua è

$$I(A;B) = H(B) -H(B|A)=H(B) \le 1$$

L’ultima disuguaglianza è dovuta al fatto che l’entropia di una variabile binaria è compresa nell’intervallo $[0,1]$. L’entropia $H(B|A)=0$ in quanto non c’e alcuna incertezza sul simbolo inviato dalla sorgente, una volta osservato il simbolo di arrivo. Il massimo valore di $I(A;B)$ viene raggiunto nel caso in cui la sorgente ha una distribuzione uniforme, cioè $p_{0}=p_{1}=\dfrac{1}{2}$. Quindi la capacità del canale è uguale ad $1$.

Esercizio 5.2 – Canale binario simmetrico
Calcolare la capacità di un canale binario simmetrico con probabilità di errore uguale a $p_{e}$.

Soluzione
Dall’esempio 4.1 abbiamo

$$I(A;B) = H(B) -H(p_{e}) \le 1 -H(p_{e})$$

Il massimo dell’informazione mutua si ha quando $H(B)=1$, cioè se la distribuzione dei simboli di output è uniforme. La capacità di un canale BSC è quindi

$$C = 1 -H(p_{e}) = 1 + p_{e}\log_{2}p_{e} + (1-p_{e})\log_{2}(1-p_{e})$$

Dimostriamo ora che nelle condizioni della definizione 5.1 il massimo dell’informazione mutua esiste.

Teorema 5.1
Se la matrice di transizione $M_{ij}$ è costante, allora la funzione $I(A,B)=H(B)-H(B|A)$ ammette un massimo valore.

Dimostrazione
La distribuzione di probabilità di $A$ può essere rappresentata da un vettore $\mathbf{p}=\{p_{1},\cdots,p_{r}\}$. L’insieme di tutte le possibili distribuzioni di probabilità è

$$T = \{\mathbf{p} \in \mathbf{R}^{r}: \sum\limits_{k=1}^{r}p_{k}=1 , p_{k}\ge 0\}$$

Si può dimostrare che l’insieme $T$ è un insieme chiuso e limitato.
Dimostriamo ora che la funzione $I(A;B)$ è una funzione continua di $\mathbf{p}$, cioè è una funzione continua delle $r$ variabili $p_{1}, \cdots,p_{r}$. In primo luogo abbiamo

$$H(B|A) = \sum\limits_{k=1}^{r}p_{k}H(B|a_{k})=\sum\limits_{k=1}^{r}p_{k} \left(\sum\limits_{j=1}^{s}P_{kj}\log_{2}\frac{1}{P_{kj}}\right)$$

La quantità tra parentesi è costante in quanto per ipotesi le probabilità di transizione $P_{ik}$ sono costanti. Quindi $H(B|A)$ è una funzione lineare continua delle variabili $p_{k}$.
La funzione $H(B)=-\sum\limits_{j=1}^{s}q_{j}\log_{2}q_{j}$ può essere vista come funzione delle $r$ variabili $p_{1}, \cdots,p_{r}$. Infatti è una funzione composta di due funzioni continue: la prima calcola le variabili $q_{j}=\sum\limits_{j=1}^{s}p_{k}P_{kj}$; la seconda è la funzione $x \log_{2}x$ che come è noto è continua nell’intervallo $[0,1]$. Essendo composta tramite due funzioni continue anche $H(B)$ è una funzione continua.
La funzione $I(A;B)= H(B)-H(B|A)$ è quindi una funzione continua su un insieme chiuso e limitato (compatto), e per il teorema di Weierstrass ammette un massimo.

---

Conclusione

In questo articolo abbiamo introdotto il concetto fondamentale di capacità di un canale dal punto di vista teorico matematico. In un prossimo articolo daremo una definizione più operativa di capacità, in termini di massima velocità possibile per trasmettere senza errori. Inoltre studieremo il secondo teorema di Shannon per determinare la massima velocità di trasmissione in un canale in presenza di rumore.

---

Bibliografia

^[1]C. Shannon, W. Weaver – The Mathematical Theory of Communication (The University of Illinois Press)

^[2]T. Cover – Elements of Information Theory (Wiley)