L’Algoritmo di Euclide, i Numeri di Fibonacci e il Teorema di Lamé

L’algoritmo di Euclide permette di calcolare il massimo comune divisore (MCD) di due numeri interi. È descritto nel Libro VII degli ‘Elementi’ di Euclide, la grande opera pubblicata intorno al 300 a.C. Nonostante l’età, resta un algoritmo molto efficiente dal punto di vista computazionale e viene ancora utilizzato con i moderni computer.
In questo articolo descriveremo l’algoritmo di Euclide e alcune sue applicazioni.

---

1) Rappresentazione degli interi con una data base

Il sistema decimale che utilizziamo per rappresentare i numeri è una della più grandi invenzioni che hanno permesso lo sviluppo della matematica. Diversamente dal sistema che usavano gli antichi Romani, nel sistema posizionale il valore di una cifra dipende dalla sua posizione.
I Babilonesi utilizzavano un sistema posizionale con base 60. Probabilmente i primi ad utilizzare il sistema decimale furono gli Indiani, i quali introdussero anche il simbolo dello zero.
L’importanza del sistema decimale venne riconosciuta dal grande matematico francese Laplace, che la considerò una delle scoperte più utili per l’umanità.
Come è noto nel sistema decimale per rappresentare i numeri si usano le cifre dell’insieme \(X= \{0,1,2,3,4,5,6,7,8,9\}\). Ogni numero intero è rappresentato con una stringa di un numero finito di cifre dell’insieme \(X\). Ad esempio

\[ 3517_{10}= 3 \cdot 10^{3}+ 5 \cdot 10^{2}+ 1 \cdot 10^{1}+ 7 \]

Tuttavia la base \(10\) non è l’unica possibile. Qualunque intero positivo \(b >1\) può essere utilizzato come base per un sistema di rappresentazione posizionale :

\[ n = a_{t}b^{t} + a_{t-1}b^{t-1} + \cdots +a_{1}b + a_{0} \]

dove i coefficienti \(a_{i}\) appartengono ad un insieme contenente \(b\) elementi.
Il sistema esadecimale con base \(b=16\) utilizza i seguenti \(16\) simboli per rappresentare le cifre: \(\{0,1,2, \cdots, 9, A,B,C,D,E,F \}\). Il sistema binario utilizza solo due simboli \(\{0,1\}\) per le cifre.
Ad esempio il numero decimale \(37\) nelle basi \(16\) e \(2\) viene così rappresentato:

\[ 37_{10}= 25_{16}= 100101_{2} \]

Esercizio 1.1
Dimostrare che si ha \( n < b^{n} \).

Teorema 1.1 – Rappresentazione dei numeri interi in una base
Sia dato un intero positivo \(b\) maggiore di \(1\). Allora per ogni intero positivo \(n\) esiste un’unica rappresentazione nella base b:

\[ n = a_{t}b^{t} + a_{t-1}b^{t-1} + \cdots +a_{1}b + a_{0} \]

dove \(a_{t} \ne 0 \) e \( 0 \le a_{i} < b\).

Dimostrazione
Per dimostrare l’unicità indichiamo con \( \alpha (n,b) \) il numero delle rappresentazioni distinte del numero \(n\) nella base \(b\). Ovviamente \(\alpha(1,b)=1 \). Osserviamo ora che per ogni rappresentazione di \(n\) possiamo trovare una rappresentazione di \(n-1\). Infatti poniamo

\[ n = a_{t}b^{t} + a_{t-1}b^{t-1} + \cdots +a_{i}b^{i} \]

dove \(a_{i}\) è il primo coefficiente non nullo della rappresentazione a partire dalle potenze inferiori (naturalmente può essere \(i=0\)). Allora

\[ n-1 = a_{t}b^{t} + a_{t-1}b^{t-1} + \cdots +(a_{i}-1)b^{i} + b^{i}-1 \]

Poiché \(b^{n} > n\) e \(b^{n}\) ha almeno una rappresentazione nella base \(b\), abbiamo

\[ 1 \le \alpha(b^{n},b) \le \alpha(n,b) \le \alpha(1,b)=1 \]

Esercizio 1.2
Sia data una rappresentazione di \(n\) in base \(b\):

\[ n = a_{k}b^{k} + a_{k-1}b^{k-1} + \cdots +a_{1}b^{1}+a_{0} \]

Dimostrare che

\[ 0 \lt n \le b^{k+1}-1 \]

---

2) Divisibilità fra numeri interi

Dato un intero \( n_{0} \in \mathbb{Z}\) definiamo l’insieme

\[ \mathbb{N}_{n_{0}}= \{ m \in \mathbb{Z}: m \ge n_{0}\} \]

L’insieme \(\mathbb{N}_{0}\) coincide con gli interi non negativi:

\[ \mathbb{N}_{0}=\{0,1,2,3, \cdots \} \]

La struttura algebrica degli interi soddisfa due principi fondamentali, tra loro equivalenti:

Principio del buon ordinamento (o del minimo)
Ogni sottoinsieme non vuoto di \(\mathbb{N}_{n_{0}}\) contiene un elemento minimo.

Principio di induzione
Sia \(X \subset \mathbf{Z}\) tale che:

\[ \begin{array}{l} n_{0} \in X \\ n \in X \Rightarrow (n+1) \in X, \quad n_{0} \le n \\ \end{array} \]

Allora l’insieme \(X\) contiene tutti gli interi maggiori o uguali a \(n_{0}\).

Dimostriamo ora il seguente fondamentale teorema di Euclide:

Teorema 2.1 – Euclide
Dato un intero \( k \gt 0\) e un intero \(n\), esistono due unici interi \(q,r\) tali che:

\[ n = kq+ r \quad 0 \le r \lt k \]

Dimostrazione
Dimostriamo prima l’esistenza. Consideriamo l’insieme

\[ S = \{n- xk | x \in \mathbb{Z}, n-xk\ge 0\} \]

Si tratta di un insieme di interi non vuoto (verificare) e limitato inferiormente, quindi esiste un elemento minimo, indicato con \(r=n-kq\), che appartiene all’insieme. Il numero \(r\) verifica le seguenti disuguaglianze

\[ 0 \le r = n-kq \lt k \]

Vediamo ora l’unicità. Supponiamo per assurdo che esistano due rappresentazioni diverse \(n=kq+r=kq_{1}+r_{1} \). Ne deriva \( r-r_{1}=k(q_{1}-q) \). Da questo ne consegue

\[ k > |r-r_{1}| = |q-q_{1}|k \ge k \]

che implica \(q=q_{1},r=r_{1}\).

---

3) Il massimo comune divisore e l’algoritmo di Euclide

Si dice che un intero \(b\) divide un intero \(a\) se risulta \(a=bq\) dove \(q\) un intero. Si usa la notazione \(b|a\). Si assume che per ogni intero non nullo \(b\) risulti \(b|0\).
Dati due interi \(a,b\), un intero \(q\) che divide entrambi si chiama divisore comune.

Definizione 3.1
Dati due interi non entrambi nulli \(a,b\), si dice che un intero d è il massimo comune divisore di \(a,b\) se:

• \(d \gt 0\)
• \(d\) è un divisore comune di \(a,b\)
• ogni altro intero che è un divisore comune di \(a,b\) divide anche \(d\)

Il massimo comune divisore di due interi \(a,b\) si indica con \(MCD(a,b)\) oppure con \( (a,b) \).

Esempio 3.1

\[ \begin{array}{l} (124,144)= 4 \\ (121,11)= 11 \\ (20,31)=1 \end{array} \]

Teorema 3.1 – Esistenza e unicità dell’MCD
Dati due interi \(a,b\), non entrambi nulli, esiste l’\(MCD(a,b)\) ed è unico.

Dimostrazione
La dimostrazione di questo teorema viene fatta mediante l’algoritmo di Euclide. L’algoritmo di Euclide dimostra e contemporaneamente calcola l’MCD, utilizzando il teorema 2.1. L’algoritmo si basa sull’osservazione che un divisore comune di due interi deve dividere anche la loro differenza.
Dati due interi \(a,b\) con \(b \gt 0\) l’algoritmo di Euclide effettua un numero finito di divisioni secondo lo schema seguente:

\[ \begin{array}{l} a = b q_{1}+ r_{1}, \quad 0 \lt r_{1} \lt b \\ b= r_{1}q_{2} + r_{2} \quad 0 \lt r_{2} \lt r_{1} \\ r_{1}= r_{2}q_{3} + r_{3} \quad 0 \lt r_{3} \lt r_{2} \\ \vdots \\ r_{n-2}= r_{n-1}q_{n} + r_{n} \quad 0 \lt r_{n} \lt r_{n-1} \\ r_{n-1}=r_{n}q_{n+1} \end{array} \]

L’algoritmo termina dopo un numero finito di passi poiché:

\[ b \gt r_{1} \gt r_{2} \gt \cdots \]

Il massimo comune divisore \( (a,b) \) di \(a\) e \(b\) è \( r_{n} \), l’ultimo resto non nullo nell’algoritmo di Euclide. Infatti proseguendo all’indietro si verifica che \(r_{n}\) divide gli altri resti \(r_{n-1},r_{n-2}, \cdots ,r_{1}\). Inoltre se un altro intero \(d\) divide \(a\) e \(b\), allora procedendo dall’inizio si vede che divide tutti i resti fino a \(r_{n}\).
L’algoritmo di Euclide quindi dimostra l’esistenza dell’MCD. D’altra parte è facile verificare anche che l’MCD deve essere unico.

In termini geometrici si può pensare all’MCD(a,b) come ad una unità di misura comune ad entrambi i numeri \(a,b\). L’algoritmo di Euclide può essere utilizzato anche per numeri razionali e irrazionali. Tuttavia l’algoritmo non termina con un numero finito di passi se i due numeri non sono commensurabili, cioè se non sono entrambi multipli interi di uno stesso numero reale. Un esempio famoso di grandezze non commensurabili è la coppia costituita da \(1\) e \(\sqrt{2}\), che rappresentano il lato e la diagonale di un quadrato di lato unitario.

---

4) Complessità dell’algoritmo di Euclide

4.1) La complessità degli algoritmi

È utile richiamare brevemente alcuni concetti relativi alla determinazione della complessità degli algoritmi.
I moderni computer utilizzano il sistema binario per rappresentare i numeri interi e i reali in generale. Supponiamo di voler sommare i numeri 15 e 21. Nel sistema binario la rappresentazione è la seguente:

\[ \begin{array}{l} 15_{10}= 1111_{2} \\ 21_{10} = 10101_{2} \end{array} \]

Per sommare due numeri binari si possono incolonnare a destra le due stringhe binarie e procedere come nel caso decimale. Le regole sono le seguenti:

\[ \begin{array}{l} 0+0 = 0 \\ 0+1 = 1 \\ 1+0 = 1 \\ 1+1 = 0 \quad \text{con riporto di 1} \\ \end{array} \]

In modo simile si effettuano le altre operazioni: sottrazione, moltiplicazione e divisione.

Esercizio 4.1
Dimostrare che il numero di cifre binarie per rappresentare un numero decimale intero \(n\) è \( \lfloor\log_2(n)\rfloor + 1\).

Nel calcolare la complessità di una operazione è importante contare il numero di operazioni sui bit (bit-operations) che vengono effettuate. La complessità temporale di un’operazione tramite computer è proporzionale al numero di operazioni binarie. Possiamo scrivere:

\[ \text {Complessità} = K \cdot \text{Numero operazioni binarie} \]

Naturalmente la costante di proporzionalità varia a seconda della potenza del computer. Tuttavia ai fini della determinazione della complessità di un algoritmo non è necessario conoscere il valore esatto della costante.

Definizione 4.1 – Notazione di Landau (1877-1938)
Siano date due funzioni \(f(n),g(n)\) che assumono valori positivi. Si dice che la funzione \(f\) è al massimo dell’ordine della funzione \(g\) e si scrive

\[ f(n) = O(g(n) \]

se esiste un intero positivo \(n_{0}\) tale che:

\[ f(n) \le M\cdot g(n) \quad \text{ se } \quad n \ge n_{0} \]

dove \(M\) è un numero reale positivo.

Come si può notare, quello che interessa è l’andamento delle funzioni per valori grandi dell’argomento \(n\), mentre non è importante studiare i valori iniziali.

Esempio 4.1

\[ \begin{array}{l} 10 n^{7} + 900n^{6}+ 5 = O(n^{7}) \\ 2^{n+1} = O(2^{n}) \\ 10^{5}n + n^{3} = O(n^{3}) \\ 100 n \log_2 (n) + n^{3} = O(n^{3}) \\ \end{array} \]

Definizione 4.2
Sia dato un algoritmo che nel caso peggiore richiede \(T(n)\) operazioni. Si dice che l’algoritmo ha complessità temporale polinomiale se risulta

\[ T(n) = O(n^{k}) \quad k \in \mathbb{N} \]

Si dice che un algoritmo ha complessità temporale esponenziale se esistono numeri reali \(\alpha \gt 0\) e \(A \gt 1\) tali che:

\[ T(n) \ge \alpha A^{n} \]

Il numero \(n\) rappresenta la dimensione del problema, ad esempio il numero di cifre di due numeri che vengono moltiplicati.

Si può dimostrare il seguente teorema:

Teorema 4.1
Siano dati due numeri \(a,b\) rappresentati con \(k,l\) cifre binarie rispettivamente. Allora la complessità per ognuna delle 4 operazioni aritmetiche effettuate con il procedimento ordinario è la seguente:

• Addizione: \(O(max(k,l))\)
• Moltiplicazione: \(O(k \cdot l)\)
• Sottrazione: \(O(max(k,l))\)
• Divisione: \(O(k \cdot l)\)

Se abbiamo due numeri decimali \( a,b\), la moltiplicazione ha una complessità uguale a \(O(\ln (a) \cdot \ln (b))\). Per effettuare la divisione di due numeri non maggiori di \(a\) la complessità è \( O(\ln^{2}a)\). Notiamo che ai fini della complessità non è importante la base del logaritmo che si utilizza.

Per approfondire lo studio della complessità degli algoritmi vedere ^[1].

4.2) Complessità dell’algoritmo di Euclide

Uno pseudocodice iterativo per l’algoritmo di Euclide è il seguente:

//  calcola MCD(a,b)    
//  supponiamo a >= b > 0

   x = a; 
   y = b;
   while (y >= 1) do
        x = qy + r     
        x = y;
        y = r;
   end(while)
   return x;

Come abbiamo visto l’algoritmo termina dopo un numero finito di iterazioni, in quanto il divisore \(b\) viene sostituito in ogni iterazione con un numero intero minore. Quindi possiamo affermare che l’algoritmo richiede \(O(b)\) iterazioni.

Teorema 4.2
Si ha sempre

\[ r_{k+2} \lt \frac{1}{2}r_{k} \]

Dimostrazione
Se \(r_{k+1} \le \frac{1}{2} r_{k}\) allora \( r_{k+2} \lt r_{k+1} \le \frac{1}{2}r_{k} \).
Se invece \(r_{k+1} \gt \frac{1}{2} r_{k}\) allora chiaramente \(r_{k}=1 \cdot r_{k+1}+ r_{k+2} \) e quindi \(r_{k+2} \lt \frac{1}{2}r_{k}\).

Mediante il teorema precedente, Finck (1841) ha dimostrato che il numero massimo di iterazioni per l’algoritmo euclideo è

\[ 2\cdot \log_{2}n+1 \]

A questo punto possiamo determinare la complessità dell’algoritmo di Euclide.

Teorema 4.3
Sia \( d=(a,b)\) con \(a \gt b\). La complessità dell’algoritmo di Euclide è

\[ O(\ln ^{3}(a)) \]

Dimostrazione
Poiché la grandezza del resto si riduce almeno della metà ogni due iterazioni, in base al teorema di Finck il numero massimo di divisioni necessarie è \(2\cdot \log_{2} a +1 \). Ogni divisione opera su numeri \( \le a\) e quindi richiede un numero di operazioni binarie \(O(\ln ^{2}(a))\). Il tempo complessivo totale è quindi \(O(\ln ^{3}(a))\).

In termini di cifre binarie, una formulazione equivalente è la seguente:

Siano dati due interi \(a,b\) che possono essere reappresentati in forma binaria con \(n\) bits, cioè \(0 \lt a,b \lt 2^{n}\). Allora la complessità dell’algoritmo di Euclide è al massimo \(O(n^{3})\).

L’algoritmo di Euclide è quindi di complessità polinomiale. Per uno studio approfondito dell’efficienza e della complessità dell’algoritmo di Euclide vedere il classico testo di Knuth^[2].

---

5) L’algoritmo esteso di Euclide

Una conseguenza immediata dell’algoritmo di Euclide è il seguente teorema, che permette di esprimere l’MCD(a,b) come combinazione lineare dei due numeri interi.

Teorema 5.1 – Bezout
Se \( (a,b)=d \), allora esistono due interi \( x,y \in \mathbb{Z} \) tali che

\[ ax + by = d \]

Dimostrazione
Basta partire dall’algoritmo di Euclide. Prendere l’ultimo resto non nullo \(r_{n}\) e proseguire all’indietro, esprimendo \(r_{n}\) come combinazione lineare dei numeri iniziali \(a,b\).

Esercizio 5.1
Calcolare i due interi \(x,y\) tali che \(d=(198,252)=198x+252y\)

Soluzione

\[ d=18; \ x=-5; \ y=4 \]

Notiamo che gli interi \(x,y\) possono essere negativi.
Il teorema di Bézout può essere utilizzato per trovare le soluzioni delle equazioni diofantee.

Definizione 5.1
Un’equazione diofantea è un’equazione nella quale sono ammesse solo soluzioni intere.

Ad esempio siano \(a,b,c \in \mathbb{Z}\); un’equazione lineare diofantea nelle due variabili \(x,y\) è la seguente:

\[ ax+by=c \]

Una soluzione è una coppia di interi \(x,y\) che soddisfa l’equazione. Le equazioni lineari normali rappresentano equazioni di rette nel piano ed hanno infinite soluzioni. Un’equazione diofantea invece può avere infinite soluzioni o nessuna soluzione. Vale il seguente teorema:

Teorema 5.2
Siano \(a,b,c\) tre interi e sia \((a,b)=d\). Allora

• l’equazione diofantea \(ax+by=c\) ammette soluzione se e solo se \(d|c\)
• se \(d|c\) e la coppia \(x_{0},y_{0}\) è una soluzione, allora l’insieme di tutte le soluzioni è dato dalle seguenti coppie di numeri \(x,y\):

\[ x= x_{0}+\frac{nb}{d}, \quad y=y_{0}-\frac{na}{d} \]

dove \(n\) assume tutti i valori interi positivi e negativi.

Dimostrazione
Dimostriamo solo il primo punto. Se \( (x,y)\) è una soluzione allora, posto \(a=hd,b=kd\), abbiamo

\[ c=hdx+kdy=d(hx+ky) \]

e quindi \(d|c\).
Viceversa supponiamo che \(c=md\) con \(m\) intero. Per il teorema di Bézout esistono due interi \(h,k\) tali che

\[ d = ah+kb \]

Molitiplicando per \(m\) otteniamo

\[ c=md = a(mh) + b(mk) \]

Quindi la coppia \((mh,mk)\) è una soluzione dell’equazione diofantea.

Esercizio 5.2
Trovare le soluzioni delle seguenti equazioni diofantee:

\[ \begin{array}{l} 29x+13y = 17 \\ 75x+38y = 1 \\ 5x – 12y = -2 \\ 75x + 38y = 10 \\ \end{array} \]

---

6) I numeri di Fibonacci e il numero aureo

Definizione 6.1
I numeri di Fibonacci sono definiti ricorsivamente in questo modo:

\[ \begin{array}{l} F_{1} = 1; \ F_{2} = 1; \\ F_{n+1} = F_{n} + F_{n-1} \quad n \gt 1 \\ \end{array} \]

I primi termini della successione sono: \( 1,1,2,3,5,8, \cdots \). Si pone in genere anche \(F_{0}=0\).

Esercizio 6.1

\[ \begin{array}{l} F_{1}+ F_{2} + \cdots + F_{n}=F_{n+2}-1 \quad n \ge 1 \\ F_{1}^{2}+ F_{2}^{2} + \cdots + F_{n}^{2}=F_{n}F_{n+1} \quad n \ge 1 \\ F_{m+n} = F_{m}F_{n+1} + F_{m-1}F_{n} \quad m \ge 1; n \ge 0 \\ \end{array} \]

Esercizio 6.2

\[ F_{n}^{2} – F_{n-1}F_{n+1}=(-1)^{n+1} \]

Teorema 6.1 – Formula di Binet
Dimostrare la seguente formula

\[ F_{n}= \frac{1}{\sqrt{5}}\left (\frac{1+\sqrt{5}}{2}\right)^{n}-\frac{1}{\sqrt{5}}\left (\frac{1-\sqrt{5}}{2}\right)^{n} \quad n \ge 1 \]

Soluzione
Risolvere l’equazione caratteristica \(t^{2}-t-1=0\) e applicare i metodi delle equazioni alle differenze finite^[3].

Teorema 6.2

\[ F_{n+5} \gt 10 \cdot F_{n} \quad n \ge 1 \]

Dimostrazione

\[ F_{n+5}=F_{n+4}+F_{n+3}= 2 \cdot F_{n+3}+F_{n+2}= \\ \vdots \\ = 21 \cdot F_{n-2}+ 13 \cdot F_{n-3} \\ \gt 10 \cdot(2 \cdot F_{n-2}+F_{n-3}) \\ = 10 \cdot F_{n} \]

Da questo deriva che il numero di cifre decimali di \(F_{n+5}\) è maggiore od uguale a quelle di \(F_{n}\). Per induzione possiamo affermare che

\[ F_{n+5t} \gt 10^{t}F_{n} \quad \quad n \gt 1; \quad t=1,2,3,\cdots \]

Definizione 6.2
Il rapporto aureo è definito come il rapporto tra due lunghezze a e b tale che

\[ (a+b): a = a: b \]

Chiamando \(x\) il rapporto \( \frac{a}{b} \), abbiamo la seguente equazione di secondo grado:

\[ x^{2}- x -1=0 \]

le cui due soluzioni sono le seguenti:

\[ x_{1}= \frac{1+ \sqrt{5}}{2} \quad x_{2}=\frac{1- \sqrt{5}}{2} \]

Definiamo numero aureo (o sezione aurea) il seguente numero irrazionale:

\[ \phi = \frac{1+\sqrt{5}}{2} \approx 1,168033 \]

Negli ‘Elementi’ di Euclide il rapporto aureo viene studiato, anche se non viene usato questo nome. Infatti nel Libro 6 Euclide mostra come dividere un segmento in “media e ultima ragione“, cioè come dividere il segmento \(AB\) in un punto \(C\) in modo che valga la proporzione:

\[ AB:AC = AC:CB \]

Un rettangolo aureo è un rettangolo in cui il rapporto delle due lunghezze \(a,b\) dei lati assume il valore del numero aureo:

\[ \frac{a}{b} = \phi = \frac{1+ \sqrt{5}}{2} \]

La seguente immagine illustra la spirale aurea disegnata dentro un rettangolo aureo. Per i dettagli vedere il link a Wolfram.

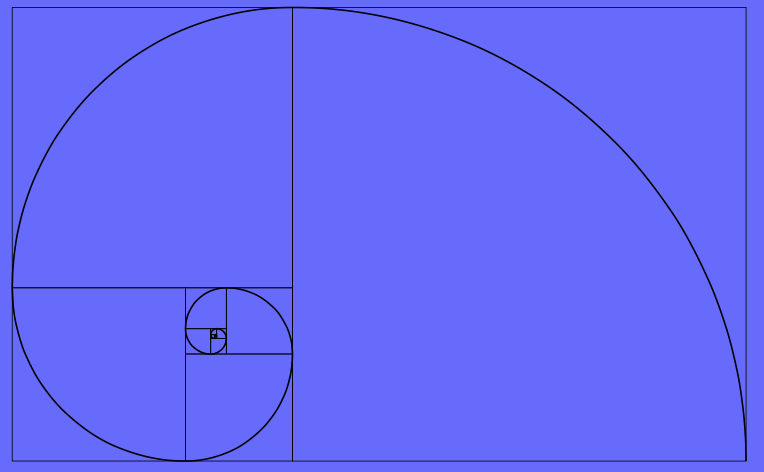
6.1) Relazione con il numero aureo

I numeri di Fibonacci hanno una stretta relazione con il rapporto aureo. Se dividiamo la formula di ricorsione per \(F_{n}\) abbiamo:

\[ \frac{F_{n+1}}{F_{n}}= 1 + \frac{F_{n-1}}{F_{n}} \]

Esercizio 6.3
Mediante la formula di Binet dimostrare che esiste il seguente limite ed è uguale al rapporto aureo:

\[ \lim_{n \to \infty}\frac{F_{n+1}}{F_{n}}=\phi = \frac{1+\sqrt{5}}{2} \]

---

7) I numeri di Fibonacci e l’algoritmo di Euclide

Applichiamo ora l’algoritmo di Euclide per calcolare l’MCD di due numeri di Fibonacci consecutivi, cioè \((a,b)=(F_{n+2},F_{n+1})\). Dalle proprietà dei numeri di Fibonacci otteniamo il seguente risultato:

\[ \begin{array}{l} F_{n+2} = 1 \cdot F_{n+1} + F_{n} \\ F_{n+1} = 1 \cdot F_{n} + F_{n-1} \\ \cdots \\ F_{4} = 1 \cdot F_{3} + F_{2} \\ F_{3} = 2 \cdot F_{2} \\ \end{array} \]

Come si vede l’algoritmo richiede \(n\) passi. Si può dimostrare che la coppia di numeri più piccoli per completare l’algoritmo di Euclide in \(n\) passi è \(F_{n+2},F_{n+1}\). Per la dimostrazione di questa proprietà utilizzeremo il risultato del seguente esercizio:

Esercizio 7.1
Dimostrare la seguente relazione, con \(a \gt b\):

\[ a -F_{k+1}=b(q_{1}-1)+ \sum\limits_{i=1}^{k-1}F_{i+1}r_{i}(q_{i+1}-1) + F_{k+1}(r_{k-1}-1) + F_{k}r_{k} \]

Teorema 7.1 – Lamé (1795-1870)
Se il numero di passi per calcolare l’MCD(a,b), con \(a \gt b\), è uguale a \(n\), allora

\[ a \ge F_{n+2} \]

Dimostrazione
Se \(n=1\) il teorema è ovvio. Se \(n \ge 2\) allora abbiamo: \(r_{n} =0, q_{n} \ge 2\). Inoltre \(q_{i} \ge 1, \ i=1,2, \cdots, n-1 \) e \(r_{i} \ge 1, \ i=1,2,\cdots, n-1\). Da questo deriva, usando l’esercizio precedente, che \(a \ge F_{n+2}\).

Teorema 7.2 – Lamé
Il numero di divisioni necessarie per calcolare l’MCD di due interi positivi con l’algoritmo di Euclide non è maggiore del prodotto fra \(5\) e il numero \(t\) di cifre decimali del più piccolo dei due numeri.

Dimostrazione
Supponiamo che per calcolare l’MCD(a,b) con l’algoritmo di Euclide siano necessari \(k\) passi:

\[ \begin{array}{l} a = b q_{1}+ r_{1} \quad 0 \lt r_{1} \lt b \\ b = r_{1}q_{2} + r_{2} \quad 0 \lt r_{2} \lt r_{1} \\ r_{1} = r_{2}q_{3} + r_{3} \quad 0 \lt r_{3} \lt r_{2} \\ \vdots \\ r_{k-3} = r_{k-2}q_{k-1} + r_{k-1} \quad 0 \lt r_{k-1} \lt r_{k-2} \\ r_{k-2} = r_{k-1}q_{k} \\ \end{array} \]

Si ha \(q_{k} \ge 2\). Quindi \(r_{k-2} \ge 2 = F_{3}\). Proseguendo abbiamo:

\[ \begin{array}{l} r_{k-3} \ge r_{k-2} + r_{k-1} \ge F_{3}+F_{2} = F_{4} \\ r_{k-4} \ge r_{k-3} + r_{k-2} \ge F_{4}+F_{3} = F_{5} \\ r_{k-5} \ge r_{k-4} + r_{k-3} \ge F_{5}+F_{4} = F_{6} \\ \vdots \\ b \ge F_{k+1} \end{array} \]

Se \(k \gt 5t\) allora \( b \ge F_{5t+2} \) e quindi per il teorema 6.2 abbiamo \( b > 10 ^{t}\), cioè \(b\) ha almeno \(t+1\) cifre decimali. Quindi se \(b\) ha \(t\) cifre decimali deve essere \(k \le 5t\).

---

Conclusione

L’algoritmo di Euclide ha grande importanza nella storia della Matematica e rappresenta la base per lo sviluppo della Teoria dei Numeri presentata da Euclide. Per la sua semplicità ed efficienza è stato ampiamente utilizzato nel corso dei secoli, e anche oggi trova applicazione nei calcoli effettuati tramite i moderni computer. Può legittimamente essere definito il padre di tutti gli algoritmi moderni.

---

Bibliografia

^[1]T. Cormen, R. Rivest, C. Leiserson, C. Stein – Introduction to Algorithms (The MIT Press)

^[2]D. Knuth – The art of computer programming: Seminumerical Algorithms (Addison Wesley)

^[3]M. Spiegel – Finite Differences and Difference Equations (McGRAW-HILL)