I numeri casuali trovano applicazione in molti settori: simulazioni, modellizzazione di sistemi complessi, programmazione di videogiochi, casinò online, crittografia, gestione di chiavi segrete per accesso ai sistemi online, ecc.
In questo articolo studieremo alcuni algoritmi utilizzati per la generazione di numeri casuali, e alcuni esempi del loro utilizzo nei giochi online e nella programmazione dei videogiochi.
1) Numeri casuali
Il concetto di numero casuale non è relativo a singoli numeri. Ad esempio non ha senso chiedersi se un singolo numero, ad esempio \(112111\) è più casuale del numero \(354611\).
Il concetto di numero casuale è invece collegato alle proprietà di una successione di numeri. Teoricamente i numeri della sequenza non dovrebbero avere alcuna correlazione. Per una definizione precisa è utile ricordare le proprietà della distribuzione uniforme.
1.1) La distribuzione uniforme
La distribuzione uniforme è la più semplice tra le distribuzioni di probabilità. Una caratteristica fondamentale di una sequenza di numeri casuali è che deve avere le caratteristiche dell’uniformità.
Nel caso di una variabile aleatoria discreta \(X\), che può assumere un numero finito di valori \(\{x_{1},x_{2}, \cdots, x_{n}\}\), ogni valore deve avere la stessa probabilità:
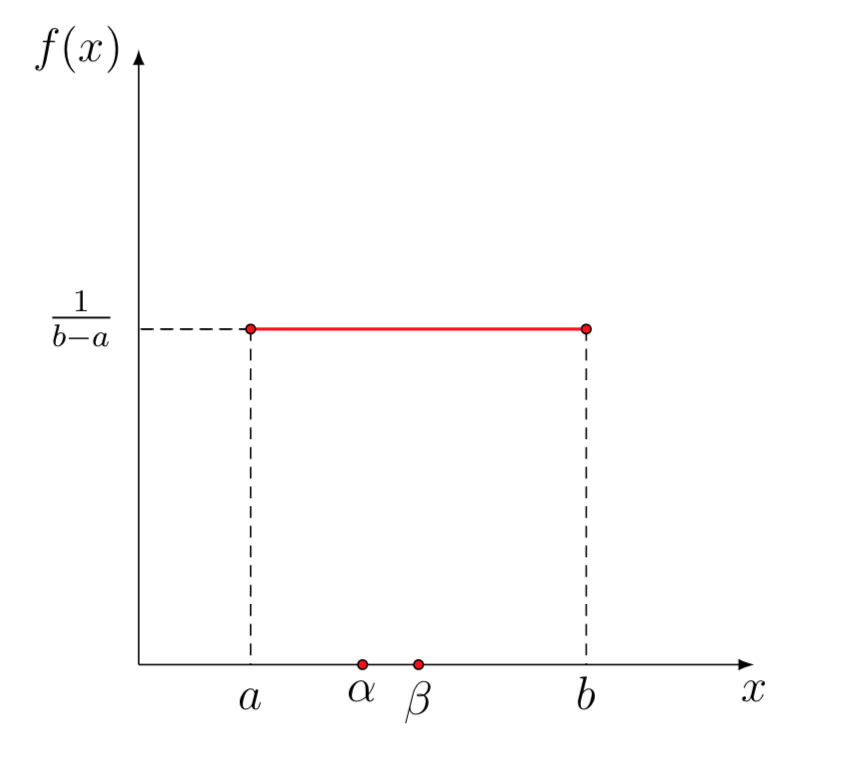
Nel caso di una variabile aleatoria continua \(X\), definita in un intervallo \([a,b]\), la distribuzione uniforme ha la seguente densità di probabilità \(f(x)\):
\[ f(x) = \begin{cases} \dfrac{1}{b-a} \quad x \in [a,b] \\ 0 \quad \quad \text{altrimenti} \\ \end{cases} \]Dati due punti \(\alpha\) e \(\beta\) compresi nell’intervallo \([a,b]\), la probabilità che la variabile aleatoria uniforme assuma valori compresi nell’intervallo è \(\dfrac{\beta – \alpha}{b-a}\).
1.2) La generazione di numeri casuali
Un generatore di numeri casuali, identificato con la sigla RNG (random number generator) può essere un dispositivo fisico o meccanico, oppure un algoritmo matematico. Naturalmente per verificare la bontà del processo di generazione è necessario analizzare una quantità grande di numeri e sottoporre il processo ad opportuni test statistici.
Esistono due categorie principali di generatori di numeri casuali:
- Pseudo Random Number Generators (PRNG)
- True Random Number Generators (TRNG)
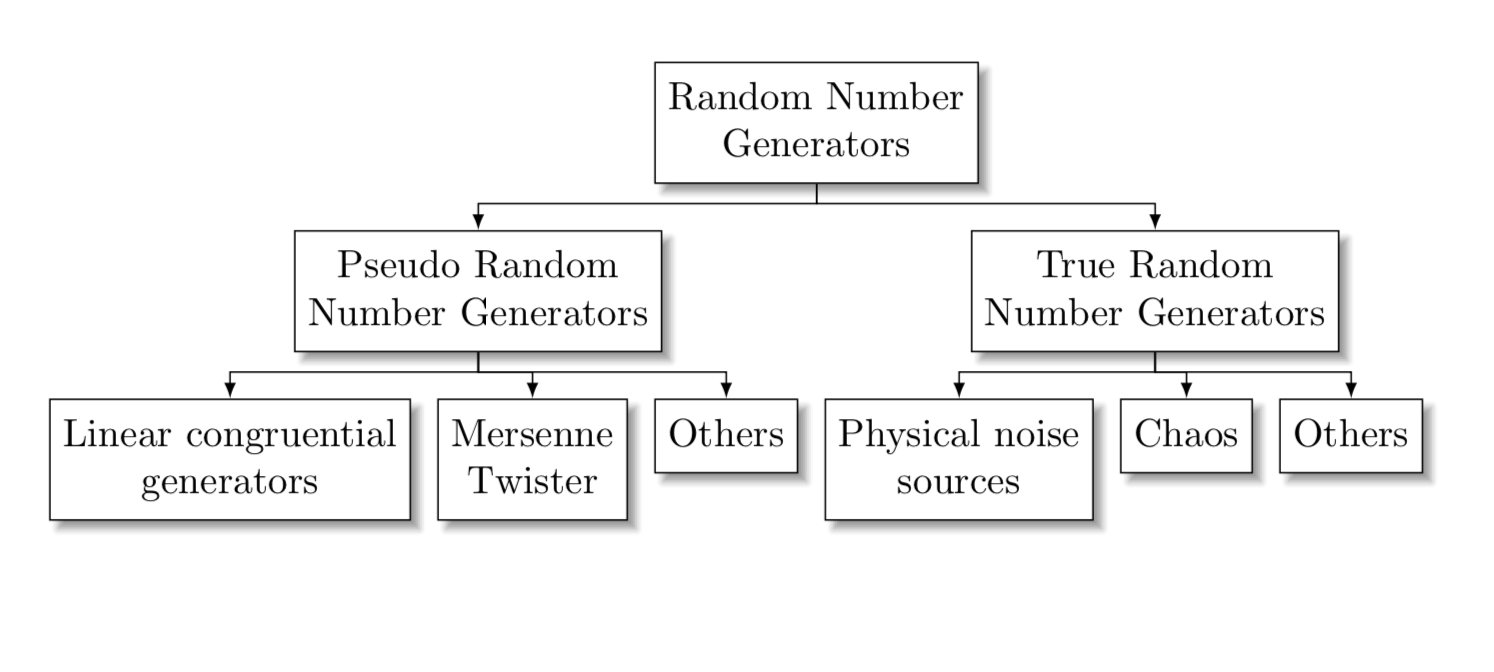
1.2.1) I generatori TRNG
I generatori TRNG generano numeri casuali a partire da fenomeni fisici di varia natura (ad esempio il rumore di fondo nell’atmosfera, il decadimento radioattivo, ecc.). La procedura consiste nel riuscire a registrare le più piccole variazioni delle grandezze fisiche associate al fenomeno fisico.
Il segnale fisico puro non sempre possiede delle caratteristiche complete di casualità. Per questo in genere viene effettuata una elaborazione aggiuntiva per migliorare le proprietà statistiche dei numeri generati. Le fasi principali di un generatore TRNG sono le seguenti:
- registrazione del fenomeno fisico e conversione in segnale elettrico
- campionamento e conversione del segnale da analogico a digitale
- adattamento del segnale alla distribuzione uniforme mediante test statistici
1.2.2) I generatori PRNG
Un generatore di numeri pseudo-casuali (PRNG) è costituito da un algoritmo deterministico che genera una sequenza di numeri. La sequenza deve naturalmente approssimare alcune proprietà caratteristiche dei numeri casuali, che vedremo nel prossimo paragrafo.
L’algoritmo prevede un input iniziale, chiamato il seme (seed) del PRNG. Ogni sequenza di numeri è completamente determinata dal seme iniziale: se si utilizza lo stesso seme iniziale la sequenza generata è sempre la stessa.
La scelta del seme iniziale è molto importante; una gestione non corretta potrebbe rendere un sistema vulnerabile ad attacchi informatici. La scelta ottimale del seme deve permettere di generare una sequenza diversa ogni volta che si esegue l’algoritmo.
1.3) Applicazioni dei numeri casuali
I numeri casuali trovano applicazioni in molti settori della scienza e della tecnologia. Tra questi ricordiamo i seguenti:
- Crittografia simmetrica e pubblica (generazione delle chiavi, password, ecc.)
- Simulazione tramite computers
- Metodo MonteCarlo per il calcolo numerico (ad esempio per il calcolo di integrali complessi, non trattabili con i metodi classici)
- Giochi d’azzardo online (dadi, carte, roulette, casinò online)
- Algoritmi probabilistici (ad esempio l’algoritmo di Miller-Rabin per verificare se un intero è primo oppure composto)
- Programmazione dei videogiochi
2) Caratteristiche di un generatore casuale
“Random numbers should not be generated with a method chosen at random.”
Donald E. Knuth
In questo articolo ci occuperemo esclusivamente di generatori pseudo-casuali. Il processo di creazione di numeri pseudo-casuali è un lavoro complesso che richiede l’utilizzo di strumenti matematici sofisticati. Un buon algoritmo PRNG deve avere alcune proprietà fondamentali:
- Uniformità: i numeri generati devono essere distribuiti in modo uniforme in un dato intervallo.
- Independenza: i numeri generati non devono presentare correlazioni fra loro.
- Lunghezza del periodo: il periodo deve avere un valore alto, prima che inizi una sequenza ripetuta.
- Replicabilità: la generazione di una sequenza di numeri deve essere replicabile (ad esempio per permettere l’attività di test).
- Velocità: chiaramente l’algoritmo deve avere una velocità adatta per le varie applicazioni.
- Utilizzo di memoria controllato.
- Sicurezza: nelle applicazioni sensibili, ad esempio nella crittografia per le comunicazioni online, non deve essere possibile prevedere il risultato dell’algoritmo.
2.1) Algoritmo di von Neumann
Nel 1946 il grande matematico ungherese John von Neumann (1903-1957) propose un algoritmo di generazione di numeri casuali, chiamato metodo del quadrato centrale. La logica dell’algoritmo è semplice: partendo da un numero, fare il quadrato e creare un nuovo numero mediante le cifre centrali. Quindi procedere di nuovo con il quadrato del nuovo numero, e così via.
Esempio 2.1
Partiamo dal numero \(x_{0}=4321\). Abbiamo:
In primi numeri della sequenza appaiono indipendenti; tuttavia spesso il metodo finisce per ripetersi dopo un ciclo finito breve. ll periodo del ciclo dipende in modo molto forte dal valore iniziale scelto (ad esempio provare con \(x_{0}=50\) oppure \(x_{0}=24\)).
Nonostante questi limiti, l’algoritmo ha la sua utilità in alcune situazioni semplici, con l’avvertenza di scegliere un valore iniziale opportuno.
Per il dettaglio dell’algoritmo di Von Neumann vedere il testo di Knuth[1].
2.2) Algoritmo di von Neumann modificato
Il difetto principle dell’algoritmo di Von Neumann è che se non si sceglie opportunamente il seme iniziale il periodo è molto piccolo, e spesso al centro c’è una sequenza di zeri. Nel 2017 Bernard Widynski ha proposto una modifica che permette di evitare molti dei limiti dell’algoritmo iniziale, superando abbastanza bene i test statistici.
Premettiamo alcune definizioni e risultati relativi alle sequenze di Weyl.
Definizione 2.1
Una sequenza di numeri reali \(\{x_{1},x_{2}, \cdots, x_{n}\}\) si dice uniformemente distribuita in un intervallo \([a,b]\), se la proporzione dei termini che si trovano in un dato sotto-intervallo qualsiasi è proporzionale alla lunghezza del sotto-intervallo stesso.
Per ogni numero reale \(x\) denotiamo con \([x]\) la parte intera di x, e indichiamo con\(\{x\}=x-[x]\) la parte frazionaria di \(x\).
Notiamo che è sempre \(0 \le \{x\} \lt 1\).
Definizione 2.2
Una sequenza di numeri reali \(\{x_{1},x_{2}, \cdots, x_{n}\}\) si dice uniformemente distribuita modulo \(1\), se la sequenza delle rispettive parti frazionarie è uniformemente distribuita nell’intervallo \([0,1]\).
Teorema 2.1 – Weyl
Dato un numero irrazionale \(\alpha\), la sequenza \(\{n\alpha\}\) è uniformemente distribuita modulo 1.
Esercizio 2.1
Dimostrare che se \(x=\dfrac{p}{q}\) è un numero razionale, allora la sequenza \(\{nx\}\) assume solo un numero finito di valori diversi e quindi non è uniformemente distribuita modulo 1.
Esercizio 2.2
Dimostrare che se la sequenza \(x_{n}\) è uniformemente distribuita modulo \(1\), allora la successione della parti frazionarie \(\{x_{n}\}\) è densa nell’intervallo \([0,1]\).
Per modificare l’algoritmo di Von Neumann, Widinski utilizza una sequenza di Weyl nella quale al posto di un numero irrazionale c’è un numero intero dispari, primo con il modulo. In genere il modulo \(m\) è una potenza di \(2\) e la sequenza di Weyl è la seguente:
\[ t,2t,3t, \cdots, \quad t \in \mathbb{N}, t \text{ dispari} \]Se \(m=2^{n}\) e \(t \lt n\) la sequenza è uniformemente distribuita modulo \(2^{n}\).
Uno schema dell’algoritmo \(C\) proposto da Widynski è il seguente:
#include <stdint.h>
uint64_t x = 0, w = 0, s = 0xb5ad4eceda1ce2a9;
inline static uint32_t msws() {
x *= x;
x += (w += s);
return x = (x>>32) | (x<<32);
}Per i dettagli sull’implementazione dell’algoritmo di Widynski vedere [2]. Per uno studio approfondito delle sequenze uniformemente distribuite e del criterio di Weyl vedere [3].
3) I generatori lineari congruenziali (LCG)
“Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin”
John von Neumann
L’approccio moderno più diffuso è la generazione di numeri pseudo-casuali mediante algoritmi eseguiti con i computer. Un tale algoritmo genera una successione di numeri che simulano una successione di variabili aleatorie indipendenti con distribuzione uniforme in un dato intervallo, ad esempio in \((0,1)\). L’approccio più semplice consiste nel calcolare una successione di numeri reali mediante una opportuna equazione congruenziale lineare:
\[ x_{n+1} = ax_{n} \pmod{m} \]dove \(a,m\) sono interi positivi e \(m \gt 1\).
L’algoritmo inizia con un valore iniziale \(x_{0}\), chiamato il seme (seed). I valori possibili della sequenza sono \((0,1, \cdots,m-1)\). Quindi dopo un numero finito di passi si ripete un valore già trovato, e la sequenza diventa periodica. Per questo è importante scegliere i parametri \(x_{0},a,m\) in modo tale che il periodo della sequenza sia molto grande.
Il comportamento del programma è deterministico; a parità di seme iniziale la sequenza di output è la stessa.
La maggior parte degli algoritmi PRNG moderni sono dei generatori congruenziali lineari. Producono una sequenza di interi compresi nell’intervallo \([0,m-1)\) mediante una opportuna equazione congruenziale lineare di questo tipo:
dove \(a\) è il moltiplicatore, \(c\) è l’incremento e \(m\) è il modulo.
Se definiamo nuove variabili \(y_{n}=\dfrac{x_{n}}{m}\) otteniamo una distribuzione uniforme nell’intervallo \([0,1]\).
La scelta dei parametri è molto importante per l’efficienza dell’algoritmo. Scartando i casi banali possiamo assumere le seguenti condizioni:
Nel caso \( c=0\) l’algoritmo è più veloce, tuttavia ha l’inconveniente di rendere più piccolo il periodo.
Esempio 3.1
Consideriamo il seguente generatore
Poniamo il seme iniziale \(x_{0}=0\). Dimostrare che il periodo è uguale a \(8\).
Esempio 3.2
Sia dato il seguente generatore
Dimostrare che partendo con il seme \(x_{0}=1\), la sequenza ha periodo massimo uguale a 16.
4) Alcuni richiami di Teoria dei Numeri
Per analizzare il comportamento dell’algoritmo LCG in funzione dei parametri è opportuno ricordare alcune definizioni e teoremi della Teoria dei Numeri.
Definizione 4.1
Sia m un intero positivo e a un intero tale che \((a,m)=1\). Si chiama ordine di a modulo m il più piccolo intero positivo \(h\) tale che
Usiamo la notazione \(ord_{m} a = h\).
Esercizio 4.1
Se \(ord_{m} a = h\) dimostrare che gli interi positivi \(k\) tali che \(a^{k} \equiv 1 \pmod{m}\) sono i multipli di \(h\).
Teorema 4.1 – Eulero-Fermat
Dati due interi positivi \(a,m\), tali che \((a,m)=1\). Allora si ha
dove \(\varphi(m)\) è la funzione di Eulero, che conta il numero degli interi \(1 \le k \le n\) che sono primi con \(m\).
Per una dimostrazione vedere un qualunque testo di teoria dei numeri oppure il seguente articolo in questo sito.
L’ordine di un intero non può essere maggiore di \(\varphi(m)\). Assume quindi importanza determinare i numeri \(a\) che hanno tale esponente. Tali numeri si chiamano radici primitive modulo \(m\).
Esercizio 4.2
Se \((a,m)=1\) allora l’ordine di \(a\) modulo \(m\) divide \(\varphi(m)\).
Si può dimostrare il seguente teorema:
Teorema 4.2
Se \(p\) è un numero primo, allora esistono \(\varphi(p-1)\) radici primitive modulo \(p\).
Non tutti gli interi positivi hanno radici primitive. Vale infatti il seguente teorema:
Teorema 4.3
Esistono radici primitive modulo \( m\) se e solo se
dove \(n\) è un intero positivo e \(p\) è un primo dispari.
Teorema 4.4
Sia \(x\) un intero dispari, e \(n \ge 3\). Allora si ha
Da questo teorema deriva quindi che non esistono radici primitive modulo \(2^{n}\), con \(n \ge 3\).
Per la dimostrazione dei teoremi precedenti si può vedere [6].
Definizione 4.2 – La funzione di Carmichael \(\lambda(m)\)
Per ogni intero positivo \(m\) definiamo la funzione \(\lambda(m)\) come il più piccolo intero positivo \(h\) tale che \(a^{h} \equiv 1 \pmod{m}\), per tutti gli interi \(a\) tali che \((a,m)=1\).
Per il teorema di Eulero-Fermat sappiamo che \(\lambda(m) \le \varphi(m)\).
Un intero \(a\), con \((a,m)=1\), si chiama elemento primitivo modulo \(m\) se \(ord_{m}a = \lambda(m)\).
Teorema 4.5
La funzione \(\lambda(n)\) verifica le seguenti proprietà:
dove il simbolo \(MCM\) indica il minimo comune multiplo.
Esercizio 4.3
Dimostrare che se \(m\) ha una radice primitiva, allora si ha \(\lambda(m)=\varphi(m)\).
Per approfondire vedere il lavoro originale di Carmichael[4].
5) Scelta ottimale dei parametri per gli algoritmi LCG
Teorema 5.1 – Lehmer
Il generatore lineare congruenziale
ammette periodo \(m\) se e solo se
- \((c,m)=1\)
- \(p|a-1\) per ogni primo che divide \(m\)
- \(4|a-1\) se \(4|m\)
Per una dimostrazione completa vedere il testo di Knuth.
È importante considerare anche il caso speciale in cui \(c=0\). In questo caso non è possibile raggiungere un periodo uguale al modulo \(m\), tuttavia l’algoritmo ha i suoi vantaggi.
Teorema 5.2
Il generatore lineare congruenziale moltiplicativo
ammette il massimo periodo possibile uguale a \(\lambda(m)\), se
- \(a\) è un elemento primitivo modulo \(m\)
- \((x_{0},m)=1\)
Dimostrazione
Dato un intero positivo \(m=\prod\limits_{k=1}^{r}p^{e_{k}}\) si può dimostrare che il periodo della congruenza lineare \((x_{0},a,m)\) è il minimo comune multiplo delle lunghezze dei periodi delle singole congruenze \( (x_{0},a,p^{e_{k}})\). Consideriamo quindi la singola congruenza
In primo luogo è necessario che \((a,p^{k})=1\), altrimenti il periodo sarebbe di lunghezza \(1\). Il periodo è il più piccolo intero \(\lambda\) tale che
\[ x_{0}=a^{\lambda}x_{0} \pmod {p^{k}} \]Questa equivale a
\[ a^{\lambda} \equiv 1 \pmod {p^{k-t}} \]dove \((x_{0},p^{k})=p^{t}\). Osserviamo che
\[ \varphi(p^{k-t})=p^{k-t-1}(p-1) \]Per il teorema di Eulero si ha quindi
\[ \lambda | p^{k-t-1}(p-1) \]Ovviamente se \((x_{0},p^{k})=1\) allora \(t=0\); poiché \(a\) è un elemento primitivo i valori \(\{1,a, \cdots, a^{\lambda -1}\}\) sono distinti modulo \(p^{k}\), e quindi il periodo è uguale a \(\lambda(p^{k})\).
Se il modulo \(m\) è un numero primo allora \(\lambda(m)=\varphi(m)=m-1\), e il massimo periodo possibile è uguale a \(m-1\).
5.1) Alcuni esempi di algoritmi LCG
Alcuni esempi di implementazione dell’algoritmo LCG sono i seguenti:
Algoritmo 32-bit di Knuth-Lewis
Questo algoritmo utilizza il modulo \(m=2^{32}\) e sfrutta l’operazione logica \(and\) (indicata con il simbolo \(\land\)) per velocizzare le operazioni modulo \(m\).
Algoritmo utilizzato nel sistema operativo UNIX
\[ x_{n+1}=(1103515245x_{n} + 12345) \pmod{2^{31}} \]Il periodo è uguale a \(2^{31}\).
Algoritmo di Lewis-Goodman-Miller
\[ x_{n+1}=7^{5}x_{n} \pmod{2^{31}-1} \]Il modulo \(m=2^{31}-1\) è un numero primo di Mersenne. Il coefficiente \(7^{5}=16807\) è una radice primitiva di \(m\). Il periodo dell’algoritmo è \(2^{31}-2\).
Algoritmo RAND – MatLab
\[ x_{n+1}=(69069x_{n} + 1) \pmod{2^{32}} \]Matlab mette a disposizione diversi algoritmi di generazione di numeri casuali. Per il dettaglio vedere questo link a Mathworks.
6) Limiti degli algoritmi LCG – L’effetto Marsaglia
Il matematico George Marsaglia (1924-2011) ha evidenziato dei seri problemi nei generatori PRNG. In particolare consideriamo sequenze consecutive di numeri contenenti ognuna \(k\) numeri:
\[ {x_{i+1},x_{i+2}, \cdots, x_{i+k}} \]In uno spazio euclideo a \(k\) dimensioni, i punti risultano allineati in iperpiani paralleli, con la distanza fra gli iperpiani costante. Nel caso \(k=2\) si tratta di rette parallele. I risultati di Marsaglia sono contenuti nel seguente teorema:
Teorema 6.1 – Marsaglia
Le sequenze di \(k\) numeri consecutivi di un algoritmo LCG, con modulo \(m\), giacciono in iperpiani paralleli di dimensione \(k-1\). Il numero degli iperpiani è minore od uguale a \(\sqrt[k]{k!m}\).
Chiaramente più piccolo è il numero degli iperpiani e meno uniforme è la distribuzione dei numeri. Al contrario sono migliori gli algoritmi per i quali il numero degli iperpiani è grande. In ogni caso questa correlazione fra i numeri è un limite fondamentale degli algoritmi LNG.
Per la dimostrazione del teorema di Marsaglia vedere [5].
7) Algoritmi di generazione di Fibonacci
Uno dei modi per migliorare i generatori LCG è di aumentare il valore massimo del periodo. In genere il valore utilizzato per \(m\) è approssimativamente la lunghezza della parola del computer. Tuttavia in alcune applicazioni è necessario poter utilizzare un valore più grande, per assicurare un maggior livello di casualità. . Una delle proposte è di utilizzare un’equazione ricorsiva lineare del secondo ordine, di questo tipo:
\[ x_{n+1}=(a_{1}x_{n}+a_{2}x_{n-1}+c) \pmod{m} \]Si devono fornire all’algoritmo due valori iniziali \(x_{0},x_{1}\), dopo di che viene generata la sequenza casuale \(x_{2},x_{3},\cdots,x_{n},\cdots\).
Questi tipi di algoritmi si chiamano algoritmi Fibonacci, in riferimento ai famosi numeri di Fibonacci.
In questo caso il valore del modulo \(m\) non pone limiti al periodo del generatore, come invece è il caso del semplice algoritmo lineare del primo ordine.
Il più semplice algoritmo di Fibonacci è il seguente:
In questo caso il periodo è in genere maggiore di \(m\), ma l’algoritmo non genera una buona sequenza di numeri casuali, e non supera i test statistici di casualità. Si può generalizzare la definizione combinando due termini non adiacienti:
\[ x_{n+1}=(x_{n-l}+x_{n-k}) \pmod{m} \]In questo caso l’algoritmo viene chiamato algoritmo di Fibonacci ritardato (lagged). I valori \(l,k\) sono i lags. Il modulo \(m\) in genere viene preso uguale ad una potenza di due \(m=2^{M}\). Si usa la notazione \(LFG(l,k,M)\).
È necessario scegliere le coppie \(k,l\) in modo opportuno, altrimenti i periodi non sono abbastanza lunghi.
7.1) Algoritmo proposto da Marsaglia
L’algoritmo proposto da Marsaglia è
\[ x_{n}=x_{n-5}+ x_{n-17} \pmod{2^{k}} \]Il periodo è uguale a \(2^{k}(2^{17}-1)\). Il seme iniziale è costituito da un vettore di \(17\) interi. Per approfondire vedere [7].
7.2) Algoritmo di Mitchell e Moore
\[ x_{n}=x_{n-24}+ x_{n-55} \pmod{m} \]dove \(m\) è un numero pari e i numeri \(x_{0},x_{1},\cdots,x_{54}\) sono interi arbitrari, ma non tutti pari.
Con il modulo \(m=2^{31}\) il periodo è circa \(2^{85}\).
8) Cenni sui test statistici
In molte applicazioni, ad esempio nella crittografia, la sicurezza dei sistemi dipende modo essenziale dalla qualità della generazione di sequenze di numeri casuali. Infatti uno degli aspetti per valutare la sicurezza di algoritmi utilizzati nella crittografia è proprio il superamento dei test statistici più efficaci a disposizione.
Due aspetti fondamentali da verificare sono la distribuzione approssimativamente uniforme e l’indipendenza fra le sequenze di numeri.
Due test statistici molto diffusi sono i seguenti:
- il test del chi-quadrato
- il test di Kolmogorov-Smirnov
I test statistici considerano l’ipotesi nulla \(H_{0}\) e l’ipotesi alternativa \(H_{1}\). L’ipotesi nulla è vera se la sequenza rispetta le caratteristiche di casualità. Il test si conclude accettando o respingendo l’ipotesi nulla.
Naturalmente un singolo test non è sufficiente; è preferibile effettuare una pluralità di test statistici, per avere una sufficiente garanzia sulla bontà di un generatore.
In un articolo successivo descriveremo in dettaglio il test del chi-quadrato e il test di Kolmogorov-Smirnov.
9) Applicazioni dei numeri casuali nei giochi online
I numeri casuali trovano applicazione sempre maggiore nella programmazione dei videogiochi e dei vari giochi online: gare automobilistiche, videogiochi di guerra, giochi da tavolo, lotterie online, ecc.
Ad esempio nei giochi offerti dai moderni casinò online le slot machines generano continuamente numeri casuali, che vengono utilizzati per decidere il risultato che appare quando il giocatore da il comando di avvio del gioco. Nei giochi di carte online i numeri casuali sono utilizzati per simulare il mescolamento del mazzo di carte.
Anche nella programmazione dei videogiochi l’utilizzo dei numeri casuali ha una diffusione sempre maggiore. Alcuni motivi per l’utilizzo dei numeri casuali nella nella programmazione dei videogiochi sono i seguenti:
- permettono di introdurre variazioni che rendono il gioco meno prevedibile e quindi più interessante;
- possono simulare un comportamento intelligente, prendendo decisioni sulla probabilità che si verifichino alcuni eventi;
- possono rendere il gioco più complesso e più coinvolgente.
Alcuni esempi di applicazioni sono i seguenti:
- generazione procedurale di sprite e texture con modifica casuale del colore, della forma, della dimensione;
- generazione procedurale e casuale di mappe, terreni, ambienti;
- modifica casuale del comportamento e delle caratteristiche dei personaggi, come le dimensioni, la velocità, ecc. Ad esempio nelle gare da corsa si possono utilizzare i numeri casuali per variare la velocità in modo non prevedibile;
- simulazione di un comportamento intelligente, con decisioni prese in ogni stato, scegliendo in modo casuale tra un insieme di possibili scelte. Questo permette di superare i limiti delle macchine a stati finite (FSM), nelle quali i comportamenti in ogni stato sono pre-programmati e quindi prevedibili.
Un esempio famoso di videogioco che fa ampio uso dei numeri casuali è rappresentato dalla serie di grande successo dei Pokémon.
Altrettanto conosciuto a livello mondiale e basato sull’RNG per la generazione procedurale dei biomi è il videogioco Minecraft.
10) Numeri casuali nell’ambiente Unity3d
Nell’ambiente Unity3D è possibile utilizzare due diverse classi per la generazione dei numeri casuali.
10.1) La classe UnityEngine.Random
La classe fornita da Unity3D è una classe statica; la stessa istanza della classe viene condivisa dai vari scripts. La generazione dei numeri casuali viene effettuata mediante la funzione Random.Range. La classe prevede anche funzioni per generare punti casuali dentro un cerchio o una sfera, oppure colori casuali. Per il dettaglio delle varie funzioni messe a disposizione vedere la documentazione Unity3D della classe UnityEngine.Random.
10.2) La classe System.Random della libreria C#
Se si ha la necessità di creare istanze diverse di un generatore di numeri casuali, si può utilizzare la classe System.Random della libreria C#.
Ogni istanza della classe System.random crea un generatore indipendente. La gestione è meno semplice, tuttavia permette un maggiore controllo e separazione fra le sequenze di numeri casuali generate.
La generazione dei numeri casuali viene effettuata mediante la funzione Random.Next.
Per i dettagli vedere la documentazione Microsoft.
Vediamo ora alcuni esempi sviluppati nell’ambiente Unity3D.
10.3) Estrazioni casuali nel gioco del lotto in Italia
In Italia ci sono \(10\) ruote del Lotto, identificate con i nomi di altrettante città italiane, più una ruota chiamata Nazionale. Le città sono Bari, Cagliari, Firenze, Genova, Milano, Napoli, Palermo, Roma, Torino, Venezia.
L’algoritmo per la generazione online dei numeri relativi ad una ruota mediante la classe UnityEngine.Random è mostrato di seguito:
public void PreparaNumeriLotto() {
int totaleNumeri = 5;
numeriEstratti = new List<int>();
while (numeriEstratti.Count < totaleNumeri) {
int numeroCasuale = UnityEngine.Random.Range(1, 91);
if (!numeriEstratti.Contains(numeroCasuale)) {
numeriEstratti.Add(numeroCasuale);
}
}
}Se si vuole utilizzare la classe System.Random di C# allora il codice è il seguente:
public void PreparaNumeriLotto() {
System.Random r = new System.Random();
int totaleNumeri = 5;
numeriEstratti = new List<int>();
while (numeriEstratti.Count < totaleNumeri) {
int numeroCasuale = r.Next(1, 91);
if (!numeriEstratti.Contains(numeroCasuale)) {
numeriEstratti.Add(numeroCasuale);
}
}
}10.4) Scelta casuale della posizione e del colore degli oggetti
Mediante semplici istruzioni è possibile modificare la posizione, la forma, il colore degli oggetti sulla scena in modo casuale, ottenendo effetti interessanti. Esempi di istruzioni sono le seguenti:
obj = Instantiate(cube,GeneratedPosition(),Quaternion.identity) as GameObject;
Color col = Random.ColorHSV(0.5f, 1.0f, 0.2f, 1f, 1.0f, 1f);
obj.GetComponent<MeshRenderer>().material.color = col;
X1 = Random.Range(1, 2);
Y1 = Random.Range(1, 2);
Z1 = Random.Range(1,2);
obj.transform.localScale = new Vector3(X1,Y1,Z1);La seguente animazione è un semplice esempio:
10.5) L’algoritmo di Fisher-Yates-Knuth nei giochi con le carte
L’algoritmo venne proposto nel \( 1938\) da Fisher e Yates, per disporre in modo casuale una collezione di oggetti. È stato in seguito studiato anche da Knuth.
Per funzionare utilizza un generatore di numeri casuali. Ad esempio per mischiare un mazzo di \(52\) carte da poker la logica è la seguente:
- genera un numero casuale \(k\) compreso fra \(1\) e \(52\)
- prendi la carta nella posizione \(k\) del mazzo e scambiala con la carta nella posizione \(52\)
- genera un numero casuale \(k\) compreso fra \(1\) e \(51\)
- prendi la carta nella posizione \(k\) del mazzo e scambiala con la carta nella posizione \(51\)
- e così via
void FYK_shuffle(int card[], int n)
{
for (int i = n-1; i >= 0; --i)
{
int k = Random.Range(0, i + 1);
temp = card[i];
card[i] = card[k];
card[k] = temp;
}
} Conclusione
Come abbiamo visto i numeri casuali sono molto importanti in diverse aree della scienza, della tecnologia, dei videogiochi, ecc. I generatori PRNG presentati in questo articolo non sono perfetti, tuttavia sono buoni per gran parte delle normali applicazioni.
La ricerca di algoritmi sempre più sicuri e affidabili è in continua evoluzione, soprattutto per le applicazioni più sensibili, come la crittografia e il controllo dell’accesso alle applicazioni online. Una nuova frontiera per avvicinarsi al modello ideale di TRNG è rappresentata da dispositivi basati sui principi della fisica quantistica.
Bibliografia
[1]D. Knuth – The Art of Computer Programming – Seminumerical Algorithms (Addison-Wesley)
[2]Bernard Widynski – Middle Square Weyl Sequence RNG (ArXiv.org, PDF)
[3]S. Miller, R. Takloo-Bighash – An Invitation to Modern Number Theory (Princeton U.P.)
[4]R.D. Carmichael – Note on a new number theory function (Bulletin of the American Mathematical Society, 16, 1910, pp. 232–238)
[5]G. Marsaglia – Random numbers fall mainly in the planes (Proceedings of the National Academy of Science, 1968, 61.1, pp. 25–28)
[6]T. Apostol – Introduction to Analytic Number Theory (Springer-Verlag)
[7]G. Marsaglia – A Current View of Random Number Generators (Elsevier Science Publishers)


0 commenti