In questo articolo vengono illustrate le proprietà delle funzioni di Eulero e di Möbius, che hanno grande importanza nella Teoria dei Numeri. Come applicazione viene descritto l’algoritmo RSA per la crittografia a chiave pubblica.
1) Funzioni aritmetiche
Una funzione aritmetica è una funzione a valori reali o complessi definita per tutti gli interi positivi. Una funzione aritmetica \(f(n)\) viene detta moltiplicativa se risulta
\[ f(nm) = f(n)f(m) \quad \forall n,m \in \mathbb{N} \mid (n,m)=1 \]Viene detta completamente moltiplicativa se la relazione vale per tutte le coppie di interi positivi \(n,m\).
Esempio 1.1
La funzione identità \(I(n)\) così definita:
dove il simbolo con le parentesi quadre indica la parte intera del numero frazionario. Questa funzione è chiaramente completamente moltiplicativa.
Sull’insieme delle funzioni aritmetiche è possibile definire un’operazione binaria, chiamata convoluzione o prodotto di Dirichlet. Date due funzioni aritmetiche \(f\) e \(g\), la convoluzione, indicata con il simbolo \(f*g\), è così definita:
\[ (f*g)(n) = \sum_{d|n}f(d)g\left(\frac{n}d\right) = \sum_{d|n}f\left(\frac{n}d\right)g(d), \]dove la sommatoria viene presa su tutti i divisori di \(n\). Si dimostrano facilmente le seguenti proprietà:
\[ f*g = g*f \] \[ (f*g)*h = f*(g*h) \]Esercizio 1.1
Dimostrare che la convoluzione \(f*g\) è una funzione moltiplicativa, se lo sono le funzioni \(f\) e \(g.\)
Esercizio 1.2
Dimostrare che per ogni funzione aritmetica \(f\) si ha:
cioè la funzione Identità è elemento neutro rispetto alla operazione di convoluzione.
2) La funzione \(\varphi(n)\) di Eulero
Se \(n\) è un intero positivo, la funzione di Eulero, indicata con \(\varphi(n)\), conta il numero degli interi positivi compresi fra \(1\) e \(n\), che sono primi con \(n\) stesso. In simboli:
\[ \varphi (n) = |\{x\in \mathbb{N} \mid 1\leq x\leq n, (x,n)=1\}| \]dove il simbolo \(|A|\) indica il numero degli elementi (o cardinalità) dell’insieme \(A\).
I primi valori dell a funzione sono \(\varphi (1)=1\), \(\varphi (2)=1\), \(\varphi (3)=2\), \(\varphi (4)=2\), ecc. Per analizzare i valori assunti dalla funzione di Eulero si può utilizzare la funzione euler_phi(n) nell’ambiente SageMath.
Se \(p\) è un numero primo si ha subito: \(\varphi(p)= p-1\). Se \(n=p^{a}\) , con \(a \in \mathbb{N}\), si trova facilmente:
Basta osservare che fra i numeri naturali compresi fra \(1\) e \(p^{a}\), quelli non primi con \(p^{a}\) sono solo i multipli di \(p\), cioè \(\{p, 2p, \cdots ,p^{a-1}p\}\). Nel caso generale vale il seguente teorema.
Teorema 2.1
Se \(n=p_1^{a_1}\cdots p_k^{a_k}\), allora
Dimostrazione
Per dimostrare il teorema utilizzeremo il principio di inclusione-esclusione. Osserviamo in primo luogo che il numero di interi positivi minori od uguali ad \(n\) e divisibili per un intero positivo \(a\) è \(\Bigl\lfloor \frac{n}{a}\Bigr\rfloor\), cioè la parte intera della divisione; se \(a,b\) sono primi fra loro, il numero degli interi positivi minori o uguali a \(n\), divisibili sia da \(a\) che da \(b\), è: \(\Bigl\lfloor \frac{n}{ab}\Bigr\rfloor\); e cosi via. Applicando il principio di inclusione-esclusione otteniamo la seguente formula:
Dalla formula si vede facilmente che per \(n \ge 3\) la funzione di Eulero è sempre pari. Un’altra conseguenza è la seguente proprietà.
Teorema 2.2
La funzione \(\varphi\) è moltiplicativa. Cioè:
Teorema 2.3 (Teorema di Eulero)
Siano dati un intero positivo \(n\) e un intero \(a\) primo con \(n\). Allora vale la seguente formula:
Come caso particolare abbiamo il piccolo Teorema di Fermat:
\[ a^{p-1}\equiv 1 \pmod{p} \]Dimostrazione
Se \(a_{1}, \cdots a_{\varphi(n)}\) è un sistema di residui ridotto modulo \(n\), allora lo è anche l’insieme \(aa_{1}, \cdots aa_{\varphi(n)}\). Moltiplicando tutti gli elementi abbiamo:
Cancellando i fattori \(a_{i}\) poiché \((a_{i},n)=1\), abbiamo il risultato voluto.
Esercizio 2.1
Dimostrare che se \(m|n\) allora \(\varphi(m) | \varphi(n)\).
Esercizio 2.2
Dimostrare che \(\varphi(n) \le 5\) se e solo se \( n \in \{1,2,3,4,5,6,8,10,12\}\)
Teorema 2.4
Dimostrare che per ogni intero positivo \(N\) esiste al massimo un numero finito di interi \(n\) tali che \( \varphi(n) = N\).
Da questo dimostrare che la funzione \(\varphi(n)\) tende all’infinito, quando n tende all’infinito.
Traccia di dimostrazione
Fissiamo un intero positivo \(K\) e supponiamo che \(n > (K!)^{K}\). Allora il numero \(n\) è divisibile da un numero primo \(p >K\), oppure da \(p^{K+1}\) per qualche primo. Nel primo caso abbiamo
mentre nel secondo caso abbiamo
\[ \varphi(n) \ge \varphi(p^{K+1})= p^{K}(p-1) \ge p^{K} > K \]Quindi in ogni caso se \( n> (K!)^{K}\) allora \(\varphi(n) \ge K\), dimostrando il teorema.
Per approfondire lo studio della funzione di Eulero si può consultare [1] e [2].
3) La funzione di Möbius
La funzione di Möbius \(\mu(n)\) è così definita:
\[ \mu(n)= \begin{cases} (-1)^{k} &\mbox{se } n=\prod_{i=1}^{k} p_{i} \\ 0 &\mbox{ altrimenti} \end{cases} \]La funzione \(\mu(n)\) quindi si annulla se il numero ha divisori quadrati. Dalla definizione segue direttamente il seguente teorema.
Teorema 3.1
La funzione \(\mu(n)\) è moltiplicativa.
Teorema 3.2
Se \(n \ge 1\) abbiamo:
Il teorema è vero per \(n=1\). Supponiamo ora \(n>1\) e \(n=p_1^{a_1}\cdots p_k^{a_k}\). In base alla definizione della funzione \(\mu(n)\), abbiamo
\[ \begin{split} \sum_{d|n} \mu(d) &= \mu(1) + \mu(p_{1})+ \cdots \mu(p_{k}) \\ &+ \mu(p_{1}p_{2})+ \cdots + \mu(p_{k-1}p_{k}) \\ & \vdots \\ &+ \mu(p_{1}p_{2} \cdots p_{k}) \\ &=\sum_{i=0}^{i=k}\binom{k}{i} (-1)^{i}=0 \end{split} \]per i teorema binomiale di Newton.
Teorema 3.3
\[ \sum_{d|n}|\mu(d)|=2^{k} \]La dimostrazione è simile alla precedente.
Teorema 3.4
\[ \varphi(n)=n \sum_{d|n} \frac{\mu (d)}{d} \]Dimostrazione
La dimostrazione segue facilmente ricordando il teorema 2.1 e le proprietà della funzione di Möbius.
Teorema 3.5
Se \(f(n)\) è una funzione moltiplicativa, allora lo è anche la funzione
Dimostrazione
Se \((n,m)=1, d|n, D|m\) allora \((d,D)=1\) e il prodotto \(c=dD\) assume i valori di tutti i divisori di \(nm\). Quindi
4) La formula di inversione di Möbius
Teorema 4.1
Date due funzioni aritmetiche \(f,g \colon \mathbb{N} \to \mathbb{R}\). Se vale la relazione
allora vale la seguente formula di inversione:
\[ g(n)=\sum_{d|n} \mu(d) f(\frac{n}{d}). \]Dimostrazione
\[ \begin{split} &\sum_{d|n} \mu(d) f(\frac{n}{d})= \sum_{d|n} \mu(d)\sum_{c|\frac{n}{d}}g(c)=\sum_{cd|n} \mu(d)g(c)= \\ &\sum_{c|n} g(c) \sum_{d|\frac{n}{c}}\mu(d) \end{split} \]La somma interna vale \(1\) se \(\frac{n}{c}=1\), altrimenti vale \(0\). Quindi l’espressione è uguale a \(f(n)\).
Vale anche il teorema inverso riportato di seguito.
Teorema 4.2
Se \(n=p_1^{a_1}\cdots p_k^{a_k}\) e
allora
\[ f(n)=\sum_{d|n}g(d) \hspace{5 mm} \forall n\geq 1 \]La dimostrazione è simile alla precedente.
Mettendo insieme il teorema 3.4 e il teorema 4.2 otteniamo subito la seguente relazione.
Teorema 4.3
\[ \sum_{d|n} \varphi(d) = n \]Esercizio 4.1
Se \(n=p_1^{a_1}\cdots p_k^{a_k}\), dimostrare la seguente formula:
Esercizio 4.2
Dimostrare la seguente formula:
Esercizio 4.3
Se \(f(n)\) è una funzione moltiplicativa, dimostrare che
Esercizio 4.4
\[ \sum_{d|n} \mu(d) \varphi(d) = \prod_{p|n} {(2-p)} \]5) Relazione con l’ipotesi di Riemann (criterio di Nicolas)
La funzione di Eulero ha diversi collegamenti con la funzione zeta di Riemann. In particolare una relazione importante con l’Ipotesi di Riemann sugli zeri della funzione zeta è data dal teorema seguente.
Teorema (Jean-Louis Nicolas)
Se l’ipotesi di Riemann è vera, allora vale la seguente relazione:
dove \(\gamma \approx 0.577 \) è la costante di Eulero-Mascheroni e \(N_{k}= \prod_ {i=1}^{k} p_{i}= 2 \cdot 3 \cdot 5 \cdots p_{k}\) è il primoriale di ordine \(k\), cioè il prodotto dei primi \(k\) numeri primi (il nome è in analogia con il fattoriale).
Viceversa, se l’ipotesi di Riemann è falsa, allora la relazione sopra descritta vale per infiniti altri valori di \(k\) e non è verificata per infiniti valori di \(k\).
Quindi una possibile strategia per dimostrare l’ipotesi di Riemann è di dimostrare la validità della reazione da un certo \(k\) in poi.
Per approfondire il criterio di Nicolas vedere [3]. Per studiare la funzione zeta di Riemann un testo eccellente è [4].
6) La crittografia RSA
L’algoritmo RSA, introdotto nel 1978 da Rivest, Shamir e Adleman, è attualmente il più diffuso sistema di crittografia a chiavi pubbliche e private. Può essere usato sia per crittografare i dati sia per gestire la firma digitale. È considerato sicuro, allo stato attuale, se sono usate chiavi abbastanza lunghe (almeno 1024 bit). La sua sicurezza si basa sulla difficoltà di fattorizzare numeri interi molto grandi.
6.1) Il teorema cinese del resto
Prima di descrivere l’algoritmo RSA è utile ricordare il seguente teorema, che ha un ruolo importante nella dimostrazione della correttezza dell’algoritmo stesso. Consideriamo il sistema di due equazioni lineari alle congruenze:
\[ \begin{cases} x \equiv a_{1} \pmod {m_{1}} \\ x \equiv a_{2} \pmod {m_{2}} \end{cases} \]Se \(m_{1},m_{2}\) sono interi positivi primi tra loro, e \(a_{1},a_{2}\) sono interi, allora il sistema ha una soluzione \(\pmod {m_{1}{m_{2}}}\). Se \(x_{0}\) è una soluzione, allora lo sono anche gli \(x=x_{0} + k m_{1}m_{2}\).
Il teorema si può estendere facilmente al caso di un sistema di \(n\) equazioni, con \(n >2\).
Per la dimostrazione vedere uno dei testi indicati nella bibliografia.
Esercizio 6.1
Risolvere il seguente sistema:
Risposta: \(x= 24 + 35k\)
6.2) Algoritmo RSA
Lo schema base della procedura RSA è il seguente:
- dati due soggetti, A e B, ognuno sceglie una coppia di numeri primi molto grandi,che vengono tenuti segreti
- il soggetto A usa la sua coppia di primi (\(p_{a},q_{a}\)) e calcola \(n_{a}=p_{a} q_{a}\). Notiamo che \(\varphi(n_{a})=(p_{a}-1)(q_{a}-1)\)
- mediante un algoritmo di generazione casuale di numeri, viene determinato un numero \(e_{a}\) tale che \(1 < e_{a} < \varphi(n_{a})\) e inoltre sia primo con \(\varphi (n_{a})\)
- quindi calcola \(d_{a}\), l’inverso di \(e_{a}\) modulo \(\varphi(n_{a})\)
In definitiva i numeri a disposizione del soggetto A sono i seguenti:
\[ \begin{cases} n_{a}=p_{a} q_{a} \\ e_{a} \quad \text{ con } \quad (e_{a},\varphi(n_{a}))=1 \\ d_{a}= e_{a}^{-1} \mod {\varphi(n_{a})} \end{cases} \]La stessa procedura esegue il soggetto B.
La chiave pubblica del soggetto A è la coppia di numeri \(K(E,A) = (n_{a},e_{a})\), che viene resa pubblica e accessibile al mondo esterno. La chiave privata è la coppia \(K(D,A) = (n_{a},d_{a})\). La chiave pubblica del soggetto B è la coppia di numeri: \(K(E,B) = (n_{b},e_{b})\), che viene resa pubblica e accessibile al mondo esterno. La chiave privata è la coppia \(K(D,B) = (n_{b},d_{b})\).
6.2.1) Fase di codifica del messaggio
Il seguente diagramma riassume le operazioni della procedura RSA:
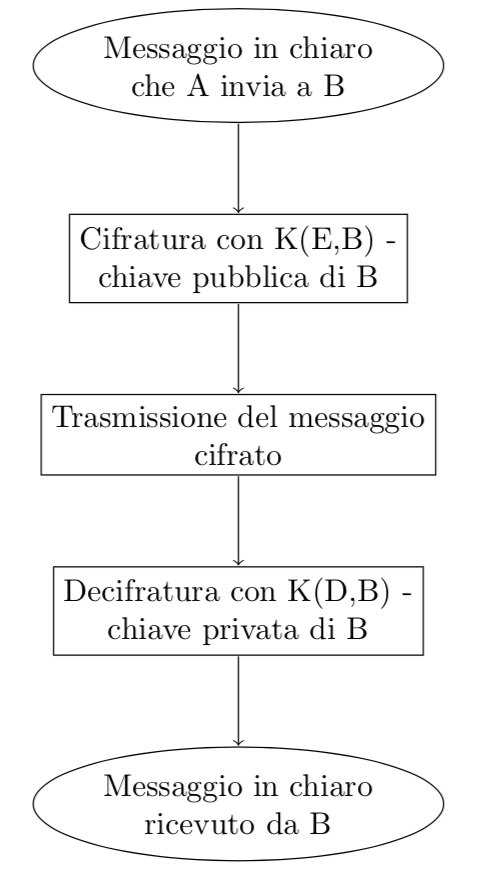
Il messaggio che deve essere cifrato viene rappresentato con un intero \(m < n\). Se l’intero è maggiore di \(n\), il messaggio viene decomposto in un insieme di messaggi separati più piccoli. Un’altra condizione è che l’intero \(m\) deve essere primo con \(n\). Si tratta comunque di un evento poco probabile in quanto se \(n=pq\) ci sono soltanto \(p+q-1\) interi più piccoli che non sono primi con \(n\), cioè i numeri \(1,p,2p, \cdots (q-1)p,q,2q, \cdots (p-1)q\); la probabilità è:
\[ \frac{p+q-1}{pq} \approx 1/p+1/q \]Essendo i primi \(p,q\) molto grandi, questa probabilità è molto piccola. Quindi per cifrare un messaggio \(m\) che A invia a B, viene utilizzata la chiave pubblica di B, mediante la seguente funzione:
\[ c \equiv m^{e_{b}}\pmod {n_{b}} \]6.2.2) Fase di decodifica
Per decifrare il messaggio crittografato \(c\), il soggetto B utilizza la funzione inversa, utilizzando la sua chiave privata.
Teorema 6.2
\[ c^{d_{b}} \equiv m \pmod{n_{b}} \]Dimostrazione
Nella dimostrazione tralasceremo l’indice \(b\) per semplicità.
Nei passaggi della dimostrazione abbiamo applicato il Teorema di Eulero, in base all’ipotesi che \(m\) è primo con \(n\).
Esercizio 6.2
Applichiamo l’algoritmo nel caso seguente: \(p=11,q=3, n= 33\).
Si ha \(\varphi (33)=20\). Scegliamo \(e=3\). Calcoliamo \(ed \equiv 1 \pmod {20}\). Si trova facilmente \(d=7\). Quindi la chiave pubblica è \(K_{3}= (33,3)\) mentre la chiave privata è \(K_{7} = (33,7)\).
Ora per crittografare un messaggio \(P=5\), calcoliamo \(C \equiv 5^{3} \pmod{33} = 26\). Per fare l’operazione inversa di decodifica e calcolare il messaggio in chiaro calcoliamo \( P \equiv 26^{7} \pmod {33} =5\).
7) Firma digitale
La procedura RSA sopra illustrata presenta tuttavia dei problemi di sicurezza. Un buon sistema di crittografia deve garantire, oltre alla sicurezza e riservatezza dei dati, anche l’autenticità dell’utente che trasmette il messaggio. Questo può essere raggiunto mediante una procedura di firma digitale che utilizza il protocollo RSA. Senza entrare nei dettagli, la schema prevede di aggiungere al messaggio crittografato con la chiave pubblica del destinatario, un altro piccolo messaggio crittografato con la chiave privata del mittente. Il destinatario, prima di decodificare il messaggio con la sua chiave privata, esegue una operazione di verifica dell’autenticità tramite la chiave pubblica del mittente. Se la verifica ha successo, procede quindi alla decifratura del messaggio con la propria chiave privata. Il seguente diagramma illustra le operazioni principali:
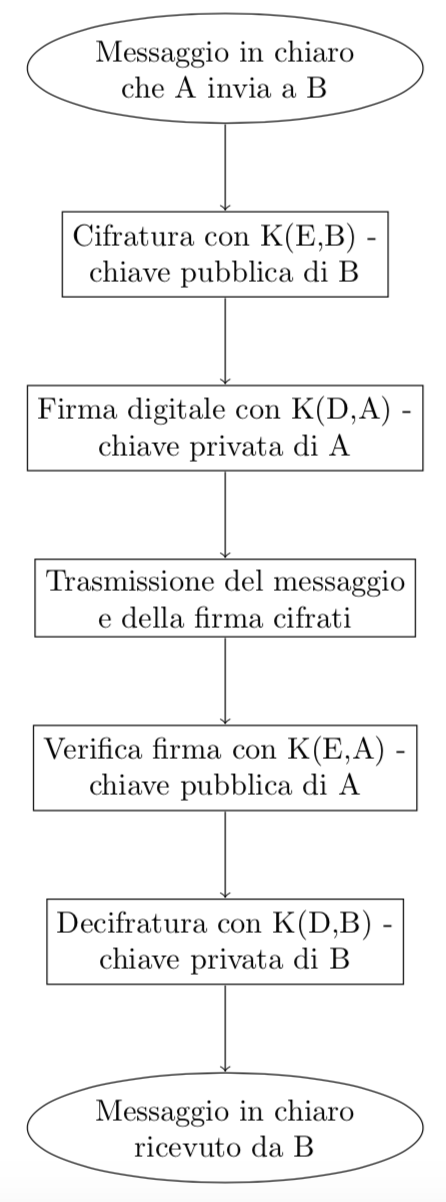
8) Sicurezza del sistema RSA
La sicurezza del sistema RSA si basa sulla difficoltà di calcolare la scomposizione in fattori primi di numeri molto grandi. Nel periodo 1993-1994 utilizzando circa 600 computers per 6 mesi si è riusciti a decifrare il codice RSA che utilizzava numeri di 129 cifre. Questo ha costretto ad aumentare la lunghezza delle chiavi. Allo stato attuale della matematica la fattorizzazione di numeri di un migliaio di cifre è praticamente impossibile, tranne in alcuni casi molto particolari. Tuttavia i progressi della matematica e la disponibilità di computer sempre più potenti da utilizzare in parallelo fanno prevedere che la procedura RSA dovrà utilizzare numeri sempre più grandi per garantire la sicurezza.
Per uno studio approfondito della matematica degli schemi di crittografia consultare [5].
9) Esercizi proposti da risolvere
Esercizio 9.1
Dimostrare che \(\varphi(n) \ge \frac{\sqrt{n}}{2}\)
Suggerimento: utilizzare le seguenti disuguaglianze:
\[ \begin{split} (p-1) > \sqrt{p} \quad (p \ge 3) \\ (n – \frac{1}{2}) \ge \frac{n}{2} \\ \end{split} \]Esercizio 9.2
Sia \(n\) un numero perfetto pari. Dimostrare che l’intero \(n-\varphi(n)\) è il quadrato di un intero.
Suggerimento: ricordare che un numero perfetto pari è della forma \(n=2^{p-1}(2^{p}-1)\), dove \(p\) è un numero primo e anche il numero \((2^{p}-1)\) è primo.
Esercizio 9.3
Trovare infiniti numeri interi \(n\) per i quali \(100 | \varphi(n)\).
Esercizio 9.4
Caratterizzare gli interi positivi \(n\) per i quali vale la relazione \(\varphi(n)=\varphi(2n)\).
Esercizio 9.5
Se \((a,b)=d\), allora
Esercizio 9.6
Definiamo la funzione di Jordan \(J_{k}(n)\), che è una generalizzazione della funzione di Eulero (\(J_{1}(n)=\varphi(n)\)):
Per ogni intero \(k \ge 1\), dimostrare che \(J_{k}(n)\) è uguale al numero delle (k+1)-uple di interi \(\{x_{1}, \cdots x_{k},n\}\) il cui massimo comune divisore è uguale a \(1\).
Bibliografia
[1]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991), pag. 190
[2]Hardy, Wright – An introduction to the Theory of Numbers, V edition (Oxford, 1979)
[3]Jean-Louis Nicolas – Small values of the Euler function and the Riemann hypothesis (ACTA ARITHMETICA 155.3, 2012)
[4]H. Edwards – Riemann’s Zeta Function (Dover)
[5]N. Koblitz – A Course in Number Theory and Cryptography (Springer)
0 commenti