Il Calcolo della Somma di Potenze di Interi Positivi – Le Soluzioni di Pascal e Bernoulli

Il problema di calcolare la somma di potenze di interi positivi è stato studiato fin dall’antichità, in particolare dai matematici greci e da Archimede. Nel corso dei secoli sono state trovate diverse formule, da Fermat, Pascal, Bernoulli e altri. In questo articolo descriviamo la soluzione di Pascal e la formula trovata da Bernoulli, che introduce i numeri di Bernoulli.

1) La somma di potenze di interi positivi

Il problema consiste nel calcolare il valore di una somma di potenze di questo tipo:

\[ S_{r}(n)=\sum\limits_{k=1}^{n}k^{r}=1^{r}+ 2^{r}+ \cdots + n^{r} \]

dove \(r=0,1,2,3,\cdots\). Possiamo definire anche \(S_{r}(0)=0\).
Le prime formule erano conosciute fin dall’antichità (greci, arabi, indiani):

\[ \begin{align} S_{1}(n)&=\sum\limits_{k=1}^{n}k^{1}=\frac{n(n+1)}{2} \label{A1}\tag{A} \\ S_{2}(n) &=\sum\limits_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6} \label{B1}\tag{B}\\ S_{3}(n) &=\sum\limits_{k=1}^{n}k^{3}=\left(\frac{n(n+1)}{2}\right)^{2} \label{C1}\tag{C}\\ \end{align} \]

Queste prime formule possono oggi essere dimostrate facilmente mediante il metodo di induzione matematica.
I pitagorici dimostrarono la prima formula \(\eqref{A1}\) con metodi geometrici, osservando che i numeri naturali consecutivi possono essere disposti per formare un triangolo, e avvicinando due triangoli si forma un rettangolo dal quale si ricava subito la formula:

Un metodo semplice per scoprire la formula consiste nello scrivere due volte la somma, la prima volta in ordine ascendente e la seconda in ordine discendente:

\[ \begin{alignat*}{6} S_{1}(n) &=1 \quad &2& \quad &3& \quad &&\cdots \quad n&-&1 \quad &&n \\ S_{1}(n) &=n \quad n&-&1 \quad n&-&2 \quad &&\cdots \quad &2& \quad &&1 \\ \end{alignat*} \]

Ogni coppia di numeri nella stessa posizione ha somma uguale a \(n+1\). Sommando tutte le \(n\) coppie troviamo nuovamente la formula indicata in precedenza:

\[ 2 S_{1}(n)=n(n+1) \]

Esercizio 1.1
Dimostrare la formula \(\eqref{A1}\) sommando la seguente identità \((m+1)^{2}-m^{2}=2m+1\), con \(m=1,2,\cdots,n\).
In particolare dimostrare la seguente identità:

\[ 1+ 3+ 5+ + \cdots + (2n-1)= n^{2} \]

La formula per la somma dei quadrati dei primi \(n\) numeri naturali è meno facile da scoprire. La formula era nota ad Archimede (288- 212 a.C). Nella sua opera ‘Sulle spirali’ presenta una formula che in notazione moderna è:

\[ 3(1^{2}+ 2^{2}+ \cdots + n^{2})= (n+1)n^{2}+ \frac{n(n+1)}{2} \]

Riordinando i termini troviamo la formula esposta in precedenza.
Dalla formula per \(S_{1}(n)\) notiamo che la somma è un polinomio di grado \(2\) con coefficienti razionali. Per calcolare \(S_{2}(n)\) si potrebbe ipotizzare che la somma sia un polinomio di grado \(3\). Un modo diretto per calcolare la somma \(S_{2}(n)\) è illustrato nel seguente esercizio.

Esercizio 1.2
Dimostrare la formula \(\eqref{B1}\) della somma dei quadrati ipotizzando che sia un polinomio di terzo grado, con coefficienti razionali.
Suggerimento: poniamo

\[ S_{2}(n)=an^{3}+bn^{2}+cn +d \]

Si può assumere \(d=0\). Determinare i coefficienti \(a,b,c\) calcolando i valori per \(n=1,2,3\).

1.1) La formula di Nicomaco per le terze potenze

Anche la somma dei cubi era nota ai greci e anche agli arabi. Questa formula è nota anche come il teorema di Nicomaco, dal nome del matematico greco Nicomaco di Gerasa vissuto intorno al \(60-120\) d.C. La formula di Nicomaco può essere dimostrata utilizzando il seguente risultato:

Teorema 1.1 – Wheatstone (1854)

\[ 1^{3}+2^{3}+\cdots + n^{3}= 1+3+ 5+ \cdots + \left(2\binom{n+1}{2}-1\right) \]

Dimostrazione
Osservare le seguenti relazioni:

\[ \begin{array}{l} 1 = 1^{3} \\ 3+5 = 2^{3} \\ 7 + 9 + 11 =3^{3}\\ \vdots \end{array} \]

Quindi procedere con il metodo di induzione.

Teorema 1.2 – Nicomaco

\[ S_{3}(n) =\sum\limits_{k=1}^{n}k^{3}=\left(\frac{n(n+1)}{2}\right)^{2} \]

Il teorema deriva immediatamente dal teorema di Wheatstone e dalla seguente formula:

\[ 1+3+5+ \cdots + (2n-1)=n^{2} \]

1.2) I numeri triangolari e la formula di Fermat per le quarte potenze

Fermat dimostrò una formula per la somma delle quarte potenze di interi utilizzando le proprietà dei numeri triangolari.
Alcuni numeri vengono chiamati triangolari, quadrati, pentagonali, ecc. poiché possono essere rappresentati mediante configurazioni di punti a forma triangolare, quadrata, pentagonale e così via. Complessivamente questi numeri vengono anche chiamati numeri figurati o poligonali. Lo studio delle proprietà dei numeri figurati ha interessato molti matematici, fin dai tempi dei greci, come Pitagora, seguito poi da Diofanto, Fermat, Eulero, Gauss, ecc.

Esempio 1.1 – Numeri triangolari
Il numero delle palline di ogni triangolo equilatero si chiama numero triangolare:

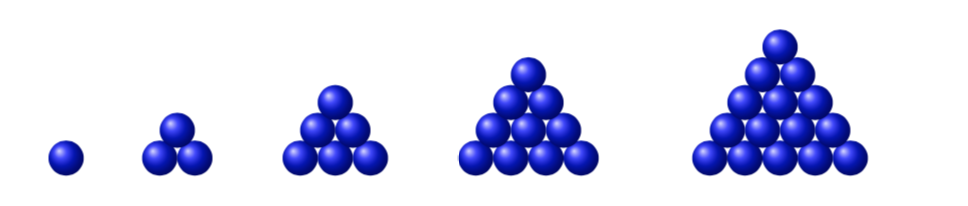
Indichiamo con \(T_{n}\) l’ennesimo numero triangolare. Dalla figura si ha subito: \(T_{1}=1\), \(T_{2}=T_{1}+2=3\), \(T_{3}=T_{2}+3\), ecc. Come si vede \(T_{n}\) soddisfa l’equazione di ricorrenza \(T_{n}=T_{n-1}+n\). Si dimostra facilmente mediante induzione l’espressione generale:

\[ T_{n}=1+2+ \cdots +n = \frac{n(n+1)}{2} \]

I numeri triangolari appaiono nel triangolo di Pascal. Nella figura sottostante sono evidenziati in neretto.

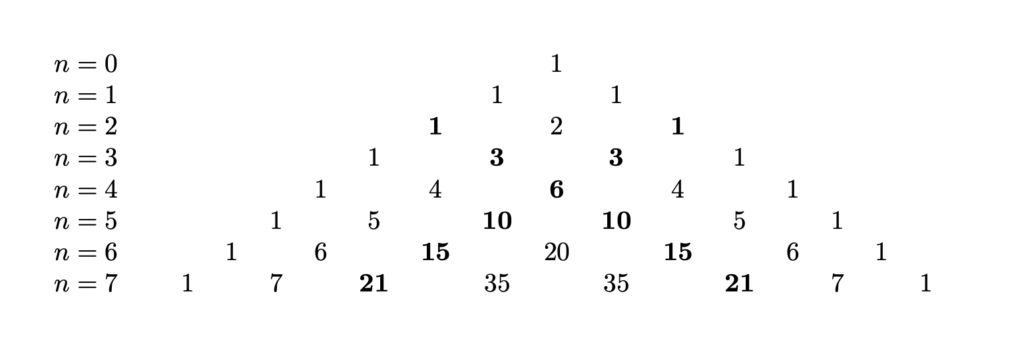
Nel \(1796\) Gauss dimostrò che ogni numero intero positivo è somma di al massimo tre numeri triangolari. Il teorema viene chiamato teorema Eureka, poiché nel suo diario Gauss espresse il teorema con la seguente formula:

\[ \text{EYPHKA!} \quad \text{Num}= \Delta + \Delta + \Delta \]

Esercizio 1.3
Dimostrare che se \(n\) è triangolare, anche il numero \(9n+1\) è triangolare.

Esercizio 1.4
Dimostrare che la somma di due numeri triangolari consecutivi è un quadrato perfetto.

Esercizio 1.5
Dimostrare le seguenti relazioni:

\[ \begin{array}{l} T_{m+n}= T_{m}+T_{n}+ mn \\ T_{mn}=T_{m}T_{n}+T_{m-1}T_{n-1}\\ \end{array} \]

Esercizio 1.6
Dimostrare le seguenti formule, ottenute calcolando i numeri triangolari modulo 2,3,5.

\[ \begin{array}{l} T(n)\pmod{2}: 1,1,0,0,1,1,0,0,1,1,\cdots \\ T(n)\pmod{3}: 1,0,0,1,0,0,1,0,0,1,0,0,\cdots \\ T(n)\pmod{5}: 1,3,1,0,0,1,3,1,0,0,1,3,10,0,\cdots \\ \end{array} \]

Vediamo ora la formula di Fermat relativa alla somma delle quarte potenze.

Teorema 1.3 – Fermat

\[ S_{4}(n)= \frac{6n^{5}+15n^{4}+10n^{3}-n}{30} \]

Suggerimento
Verificare la seguente la formula, ricordando che \(T_{n}=S_{1}(n)\):

\[ (4n+2)T_{n}^{2}=S_{2}(n)+5S_{4}(n) \]

Quindi semplificare e arrivare al risultato desiderato.

2) La soluzione di Pascal nel caso generale

Nonostante la vastità dei suoi interessi, Pascal è noto soprattutto per il triangolo aritmetico, presentato nel suo ‘Trattato sul Triangolo Aritmetico’ del 1654. Le prime righe del triangolo sono le seguenti:

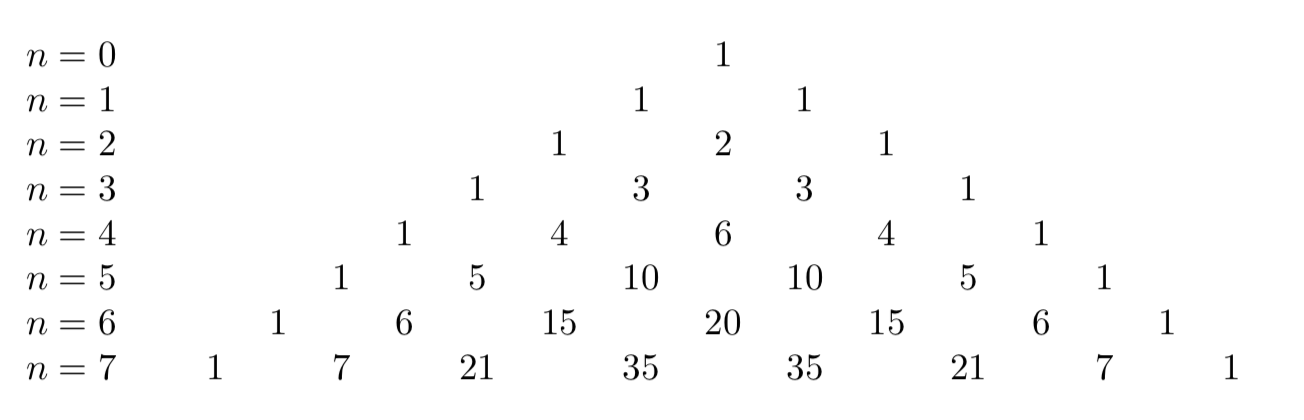
Come si vede ogni numero che non si trova sui lati del triangolo è ottenuto sommando i due numeri adiacenti che si trovano sulla riga superiore.
I numeri del triangolo di Pascal corrispondono ai coefficienti ottenuti nello sviluppo della potenza di un binomio. Ad esempio nella seconda e la terza riga troviamo i coefficienti dei seguenti sviluppi:

\[ \begin{array}{l} (a+b)^{2}= a^{2}+ 2ab + b^{2} \\ (a+b)^{3}=a^{3} + 3a^{2}b + 3ab^{2}+ b^{3} \\ \end{array} \]

I coefficienti negli sviluppi binomiali sono chiamati coefficienti binomiali. Il coefficiente del monomio \( a^{k}b^{n-k}\) nello sviluppo di \((a+b)^{n}\) viene indicato con il simbolo binomiale \(\displaystyle\binom{n}{k}\). Ricordiamo che la formula generale per lo sviluppo del binomio è la seguente (formula di Newton):

\[ (a+b)^n = \sum_{k=0}^{n}\binom{n}{k} a^{k} b^{n-k} \]

Come è noto il coefficiente binomiale \(\displaystyle\binom{n}{k}\), dove \(n,k\) sono interi positivi, rappresenta il numero delle combinazioni semplici di \(n\) oggetti presi a \(k\) a \(k\), o in modo equivalente è il numero dei sottoinsiemi di ordine \(k\) che possono essere costruiti con \(n\) oggetti. Si definisce anche \(\displaystyle\binom{n}{0} = 1\). Si possono facilmente dimostrare le seguenti formule:

\[ \begin{array}{l} \displaystyle \binom{n}{k}= \frac {n!}{k!(n-k)!} \\ \\ \displaystyle \binom{n}{k}=\binom{n-1}{k} + \binom{n-1}{k-1} \\ \end{array} \]

Naturalmente la seconda formula corrisponde alla regola di costruzione del triangolo di Pascal.
Per la storia e le proprietà del triangolo aritmetico vedere il libro di Edwards ^[1] e consultare Boyer ^[2].

2.1) La somma di potenze dei termini di una progressione aritmetica

Nel suo trattato ‘Potestatum Numericarum Summa’ del \(1654\) Pascal studiò il problema più generale di una sequenza di numeri di una progressione aritmetica. La formulazione del problema è la seguente:

“Data una arbitraria sequenza di numeri di una progressione aritmetica, ognuno elevato alla stessa potenza intera, trovare la somma di queste potenze”.

Per illustrare il suo metodo nel suo trattato, Pascal mostra l’esempio della progressione aritmetica \(\{5,8,11,14\}\), di radice uguale a \(3\), e calcola la somma seguente:

\[ S= 5^{3}+8^{3}+11^{3}+14^{3} \]

Pascal introduce la variable \(A\) ed espande il binomio \((A+3)^{4}\) mediante il teorema binomiale (notiamo che la potenza \(4=3+1\) è il valore successivo delle potenze da calcolare):

\[ (A+3)^{4}-A^{4}=+12A^{3}+54A^{2}+108A +81 \]

Sostituendo i valori \(14,11,8,5\) nella variabile \(A\) abbiamo:

\[ \begin{alignat*}{5} 17^4 &- 14^4 &&= 12 \cdot 14^3 &&+ 54 \cdot 14^2 &&+ 108 \cdot 14 &&+ 81\\ 14^4 &- 11^4 &&= 12 \cdot 11^3 &&+ 54 \cdot 11^2 &&+ 108 \cdot 11 &&+ 81\\ 11^4 &- 8^4 &&= 12 \cdot 8^3 &&+ 54 \cdot 8^2 &&+ 108 \cdot 8 &&+ 81\\ 8^4 &- 5^4 &&= 12 \cdot 5^3 &&+ 54 \cdot 5^2 &&+ 108 \cdot 5 &&+ 81\\ \end{alignat*} \]

A questo punto sommiamo le \(4\) equazioni. Le coppie a sinistra sono telescopiche e quindi la somma a sinistra si semplifica. Otteniamo perciò

\[ \begin{array}{l} 17^4 – 5^4 = \\ 12 \cdot (\color{blue}{14^3 + 11^3 + 8^3 + 5^3}) + \\ 54 \cdot (14^2 + 11^2 + 8^2 + 5^2) + \\ 108 \cdot (14 + 11 + 8 + 5) + 4 \cdot 81. \end{array} \]

Poiché conosciamo il valore delle somme con gradi inferiori a \(3\) possiamo risolvere l’equazione e trovare il valore della somma \(S\):

\[ S = \frac{83521 – 26977}{12} = 4712 \]

Il metodo di Pascal si può applicare in tutta generalità, cambiando l’esponente delle potenze e la radice.

2.2) La soluzione di Pascal al problema della somma di potenze di interi

Il metodo di Pascal può essere chiaramente applicato per il calcolo della somma di potenze di interi positivi consecutivi, considerata come una progressione aritmetica di radice uguale ad \(1\). Illustriamo il metodo per il calcolo di \(S_{2}(n)\). Dal teorema binomiale sappiamo che

\[ (n+1)^{3}-n^{3}=3n^{2}+3n+1 \]

Possiamo quindi scrivere le seguenti identità:

\[ \begin{array}{l} (n+1)^3 – n^3 = 3n^2 + 3n + 1\\ n^3 – (n-1)^3 = 3(n-1)^2 + 3(n-1) + 1\\ (n-1)^3 – (n-2)^3 = 3(n-2)^2 + 3(n-2) + 1\\ \vdots\\ 2^3 – 1^3 = 3 \cdot 1^2 + 3 \cdot 1 + 1\\ 1^3 – 0^3 = 0^2 + 3 \cdot 0 + 1 \end{array}{l} \]

Sommando le varie espressioni e semplificando otteniamo

\[ \begin{equation}{(n+1)^3 = 3 \cdot \color{blue}{\sum_{k=0}^n k^2} + 3 \cdot \sum_{k=0}^n k + n + 1.}\tag{2} \end{equation} \]

A questo punto possiamo trovare il valore della somma \(S_{2}(n)\) (somma in colore blu):

\[ \begin{align} \color{blue}{\sum_{k=0}^n k^2} &= {1 \over 3} \left((n+1)^3 – n – 1 – 3 \cdot \sum_{k=0}^n k \right)\\ &= {1 \over 3} \left(n^3 + 3 n^2 + 2n – 3 \cdot {n(n+1) \over 2} \right)\\ &= {1 \over 6} \left(2\left(n^3 + 3 n^2 + 2n\right) – 3n(n+1) \right)\\ &= {1 \over 6} n(n+1)(2n+1) \end{align} \]

Il seguente teorema illustra la formula generale di Pascal:

Teorema 2.1 – Pascal

\[ \begin{equation}{(n+1)^{p+1} – 1 = \sum_{k=0}^p \binom{p+1}{k} S_k(n)}\tag{3} \end{equation} \]

In forma estesa la formula è

\[ \begin{array}{l} (n+1)^{p+1}-1=\binom{p+1}{0}S_{0}(n)+ \binom{p+1}{1}S_{1}(n)+ \cdots + \binom{p+1}{p-1}S_{p-1}(n)+ \binom{p+1}{p}\color{blue}{S_{p}(n)} \end{array} \]

Dimostrazione
Per la dimostrazione scrivere la seguente identità in base al teorema binomiale:

\[ \begin{array}{l} (x+1)^{p+1}- x^{p+1}=(p+1)x^{p} + \binom{p+1}{2}x^{p-1} + \cdots + (p+1)x +1 \end{array} \]

per i valori \(x=n,n-1, \cdots, 1,0\). Quindi sommare e semplificare i termini della somma telescopica.
Dalla formula precedente possiamo ricavare l’espressione per la somma \(S_{p}(n)\) (somma in colore blu).

Il metodo di Pascal si basa sostanzialmente sull’osservazione che la somma \(S_{p}(n)\) è un polinomio di grado \(p+1\) con coefficienti razionali. Il coefficiente di \(n^{p+1}\) è uguale a \(\dfrac{1}{p+1}\) e la somma di tutti i coefficienti è uguale ad \(1\). Quindi abbiamo la seguente formula generale:

\[ S_{p}(n)= \sum\limits_{i=1}^{n}i^{p}=\frac{n^{p+1}}{p+1}+ \frac{n^{p}}{2}+ a_{p-1}{n^{p-1}}+ \cdots + a_{1}n \ ,\quad p \ge 1 \quad \label{2.1}\tag{2.1} \]

dove i coefficienti \(a_{p-1}, \cdots a_{1}\) sono numeri razionali da determinare.

Esercizio 2.1
Dimostrare che la somma dei coefficienti del polinomio \(S_{p}(n)\) è uguale a \(1\).

Esercizio 2.2

\[ \begin{array}{l} n = S_{0}(n) \\ n^{2}= 2 S_{1}(n) – S_{0}(n)\\ n^{3}= 3 S_{2}(n) – 3S_{1}(n) + S_{0}(n)\\ n^{4}= 4 S_{3}(n) – 6S_{2}(n) +4 S_{1}(n) – S_{0}(n)\\ \end{array} \]

Esercizio 2.3
Dimostrare la seguente formula:

\[ \begin{array}{l} \displaystyle n^{k}=\binom{k}{1}S_{k-1}(n) – \binom{k}{2}S_{k-2}(n) +\binom{k}{3}S_{k-3}(n) – \cdots +(-1)^{k-1}\binom{k}{k}S_{0}(n) \end{array} \]

Esercizio 2.4
Dimostrare la seguente formula per la somma delle quinte potenze:

\[ \begin{array}{l} \displaystyle S_{5}(n)= 1^{5}+2^{5}+ \cdots + n^{5}=\frac{n^{2}(n+1)^{2}(2n^{2}+2n-1)}{12} \end{array} \]

2.3) Interpretazione geometrica – Calcolo degli integrali

Pascal ha dato importanti contributi in molti settori della matematica. In particolare, mediante i suoi studi sulla teoria degli indivisibili risolse molti problemi di calcolo della aree e dei volumi, dando un contributo importante allo sviluppo del calcolo integrale, completato in seguito da Newton e Leibniz.
In particolare Pascal utilizzò i risultati sul calcolo delle somme di potenze per calcolare alcuni integrali particolari. Pascal sostanzialmente introdusse quelle che oggi sono chiamate somme di Riemann, per calcolare le aree di alcune figure piane e quindi gli integrali definiti.
Supponiamo che sia data una funzione continua \(f(x) \ge 0\) nell’intervallo \([0,1]\). L’area sottesa dalla curva può essere calcolata mediante l’integrale \(\int_{0}^{1}f(x)dx\). L’integrale si può approssimare mediante questa somma:

\[ \int\limits_{0}^{1}f(x)dx \approx \frac{1}{n}\sum\limits_{k=0}^{n}f\left(\frac{k}{n}\right) \]

In particolare Pascal utilizzò la formula \(\eqref{2.1}\) per calcolare l’area sottesa dalla funzione \(y=x^{k}\), con \(k\) intero positivo.

Esempio 2.1
Calcoliamo l’area sottesa dalla parabola \(y=x^{2}\) nell’intervallo \([0,1)\).

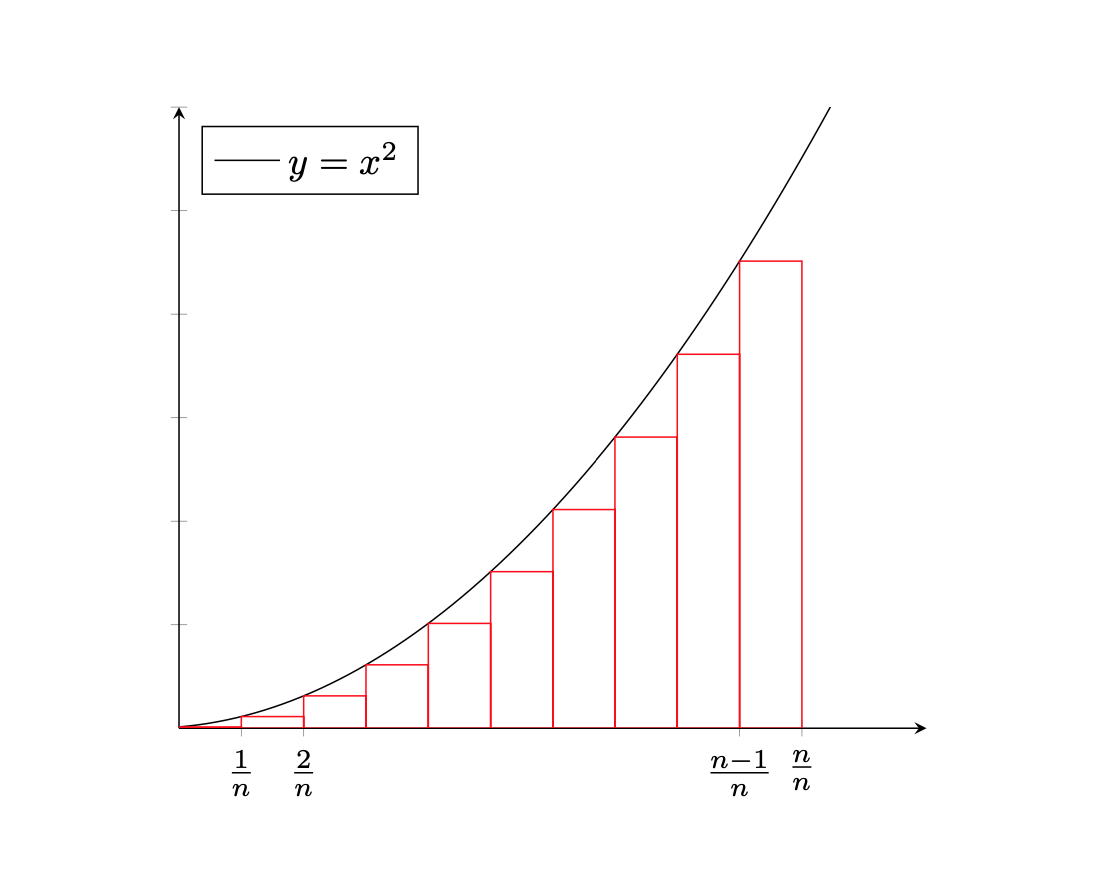
Dividiamo l’intervallo in \(n\) parti uguali nei punti \(\left\{x_{k}=\dfrac{k}{n},\ k=0,1,\cdots, n\right\}\) e calcoliamo la seguente somma:

\[ S_{2}(n) = 1^{2}+ 2^{2}+ \cdots + (n-1)^{2}= \frac{(n-1)^{3}}{3}+ \cdots \text{termini di grado inferiore} \]

La funzione viene calcolata nei punti \(x_{k}\). Per calcolare la somma delle aree dei rettangoli che approssimano l’area sottesa dalla parabola, dividiamo l’espressione \(S_{2}(n)\) per \(n^{3}\) e trascuriamo i termini di grado inferiore a tre, in quando sono grandezze infinitesimali di ordine inferiore, all’aumentare del numero \(n\). L’area sottesa dalla parabola è quindi

\[ \text{Area }= \lim_{n \to \infty}\frac{S_{2}(n)}{n^{3}}=\frac{1}{3} \]

Pascal si rifà al metodo delle grandezze indivisibili, utilizzato da vari matematici dell’epoca, per il calcolo delle aree e dei volumi. Possiamo considerare gli “indivisibili” come i “differenziali” del moderno calcolo differenziale e integrale.
Il metodo di Pascal è equivalente al calcolo del limite di una somma di Riemann. In questo caso la somma di Riemann è la seguente:

\[ S = \sum\limits_{k=0}^{n-1} \frac{1}{n} \left(\frac{k}{n}\right)^{2} = \frac{1}{n^{3}} (1^{2}+ 2^{2}+ \cdots + (n-1)^{2}) \]

L’area sottesa dalla parabola è il limite della somma di Riemann quando \(n \to \infty\). Come si vede tale limite è uguale ad \(\dfrac{1}{3}\).

Esercizio 2.5
Dimostrare la seguente formula:

\[ \lim_{n \to \infty}\frac{1^{p}+ 2^{p}+ \cdots + n^{p}}{n^{p}+n^{p}+ \cdots + n^{p}}= \frac{1}{p+1} \]

Considerare prima i casi \(p=2,p=3\).

Esercizio 2.6
Utilizzando l’esercizio 2.5 e facendo uso della definizione di integrale con le somme di Riemann, dimostrare che

\[ \int\limits_{0}^{1}x^{p}dx = \frac{1}{p+1} \ ,\quad p \in Z_{+} \]

Esercizio 2.7

\[ \int_{0}^{t}x^{k}dt = \frac{t^{k+1}}{k+1} \ ,\quad t \gt 0 \]

3) I numeri di Bernoulli

Il metodo di Pascal per calcolare \(S_{k}(n)\) richiede di conoscere le espressioni per le somme con potenze inferiori \(S_{1}(n), S_{2}(n), \cdots, S_{k-1}(n)\). Si tratta di un metodo ricorsivo importante, che viene utilizzato spesso dai matematici in molte situazioni diverse. La natura ricorsiva del metodo non permette tuttavia di effettuare un calcolo veloce della somma \(S_{k}(n)\).
Una formula unica per esprimere la somma delle potenze di interi venne trovata per primo dal matematico Jacob Bernoulli (1654-1705), nella sua opera ‘Ars Conjectandi’. Nella formula vennero introdotti dei coefficienti che in seguito saranno chiamati numeri di Bernoulli.
Per studiare le formule con i numeri di Bernoulli è preferibile introdurre il simbolo \(s_{k}(n)\), per indicare la somma senza l’ultima potenza \(n^{k}\):

\[ s_{k}(n)= S_{k}(n-1)=1^{k}+2^{k}+ \cdots + (n-1)^{k} \]

3.1) Definizione di Eulero dei numeri di Bernoulli

Esistono diversi modi equivalenti per definire i numeri di Bernoulli. Eulero propose nel \(1755\) la seguente definizione: i numeri di Bernoulli sono i coefficienti delle sviluppo in serie di Taylor-MacLaurin della seguente funzione:

\[ \frac{x}{e^{x}-1}=\sum\limits_{k=0} ^{\infty}\frac{B_{k}}{k!}x^{k} \]

I valori dei numeri iniziali di Bernoulli sono i seguenti:

\[ \begin{array}{|l|l|} \hline B_{0}= 1 & B_{1}= -\dfrac{1}{2} \\ \hline B_{2}= \dfrac{1}{6} & B_{3}= 0 \\ \hline B_{4}= -\dfrac{1}{30} &B_{5}= 0 \\ \hline B_{6}= \dfrac{1}{42} &B_{7}=0 \\ \hline B_{8}= -\dfrac{1}{30} &B_{9}=0 \\ \hline B_{10}= \dfrac{5}{66} &B_{11}=0 \\ \hline \end{array} \]

Possiamo calcolare i primi numeri di Bernoulli mediante lo sviluppo di Taylor della funzione \(F(x)=\dfrac{x}{e^{x}-1}\), come \(\lim_{x \to 0}\dfrac{d^{n}}{dx^{n}}F(x)\). Ad esempio

\[ \begin{array}{l} \lim_{x \to 0}F(x)=1 \\ \lim_{x \to 0}F'(x)=\lim_{x \to 0}\dfrac{xe^{x}-e^{x}+1}{(e^{x}-1)^{2}}=-\dfrac{1}{2} \\ \end{array} \]

Esercizio 3.1
Dimostrare che i primi termini dello sviluppo di Taylor nel punto \(x=0\) sono i seguenti:

\[ F(x)= \sum\limits_{n=0}^{\infty}\frac{F^{(n)}(x)x^{n}}{n!}= 1 -\frac{x}{2}+ \frac{x^{2}}{12}+\frac{x^{4}}{720} +\frac{x^{6}}{30240}+ \cdots \]

Esercizio 3.2
Dimostrare che

\[ \frac{x}{e^{x}-1}= \frac{x}{2}(\coth \frac{x}{2}-1) \]

dove \(\coth x=\dfrac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\) è la cotangente iperbolica.

Esercizio 3.3
Dimostrare che i numeri di Bernoulli con indice dispari sono tutti nulli, ad eccezione di \(B_{1}\).

Suggerimento
In primo luogo osservare che la cotangente iperbolica è una funzione dispari, cioè \(\coth (-x) =- \coth x\). Quindi utilizzare l’esercizio precedente e considerare la funzione \(f(x)= \dfrac{x}{e^{x}-1}+ \dfrac{x}{2}\).

Teorema 3.1
I numeri di Bernoulli soddisfano la seguente relazione:

\[ \begin{array}{l} B_{0}= 1 \\ \displaystyle \sum\limits_{k=0} ^{n-1}\binom{n}{k}B_{k}=0 \ ,\quad n \gt 1 \end{array} \]

Dimostrazione
Confrontare i coefficienti di entrambi i membri dell’identità \(x=(e^{x}-1)F(x)\).

La formula precedente può essere scritta in forma compatta in questo modo:

\[ (B+1)^{n}=B^{n} \ ,\quad n \gt 1 \]

dove il membro di sinistra viene espanso con il teorema binomiale e le potenze \(B^{k}\) vengono poste uguali ai numeri \(B_{k}\).

Esempio 3.1
Nel caso \(n=2\) abbiamo

\[ B_{2}+ 2B_{1} + 1 = B_{2} \implies B_{1}=-\dfrac{1}{2} \]

Con lo stesso procedimento dimostrare che \(B_{2}=\dfrac{1}{6}\).

Esercizio 3.4
Dimostrare la seguente formula:

\[ \begin{array}{l} \displaystyle B_{n}= \frac{-1}{n+1} \sum\limits_{k=0} ^{n-1}\binom{n+1}{k}B_{k} \ ,\quad n \ge 1 \end{array} \]

3.2) La formula di Bernoulli

La formula di Bernoulli per il calcolo di \(s_{k}(n)\) è data dal seguente teorema:

Teorema 3.2 – Bernoulli
Supponendo di utilizzare il valore \(B_{1}=\dfrac{1}{2}\), la formula di Bernoulli è la seguente:

\[ \begin{array}{l} s_{k}(n)=\sum\limits_{i=1}^{n-1}i^{k}= \dfrac{1}{k+1} \sum\limits_{i=0}^{k}\binom{k+1}{i}B_{i}n^{k+1-i} \ ,\quad k \ge 1 \end{array} \]

Dimostrazione
Consideriamo le seguenti serie di potenze:

\[ \begin{array}{l} \sum\limits_{k=0}^{\infty}\dfrac{s_{k}(n)x^{k}}{k!}=\sum\limits_{k=0}^{\infty}\dfrac{x^{k}}{k!} \sum\limits_{j=0}^{n-1}j^{k}= \sum\limits_{j=0}^{n-1}e^{xj}=\dfrac{e^{nx}-1}{e^{x}-1} \end{array} \]

Possiamo scrivere ora

\[ \begin{array}{l} \dfrac{e^{nx}-1}{e^{x}-1}= \dfrac{e^{nx}-1}{x} \dfrac{x}{e^{x}-1}= \left(\sum\limits_{k=1}^{\infty}\dfrac{n^{k}x^{k-1}}{k!}\right)\cdot \sum\limits_{j=0}^{\infty}\dfrac{B_{j}x^{j}}{j!} \end{array} \]

Eguagliando i coefficienti di entrambi i membri dell’equazione otteniamo il risultato del teorema.

Esercizio 3.5
Ricalcolare le somme \(S_{2}(n),S_{3}(n),S_{4}(n)\) utilizzando la formula di Bernoulli.

Esercizio 3.6
Dimostrare che la formula di Bernoulli può essere scritta in questo modo:

\[ \begin{array}{l} \displaystyle s_{k}(n) = \sum\limits_{i=0}^{k}\binom{k}{i}B_{k-i}\dfrac{n^{i+1}}{i+1} \end{array} \]

3.3) Soluzione tramite notazione simbolica

Consideriamo ora lo sviluppo binomiale \((x+B)^{k}\). Le grandezze \(B^{0},B^{1},B^{2}, \cdots, B^{k}\), da non interpretare come potenze, sono legate dalla relazione

\[ (B+1)^{i}=B^{i} \ ,\quad i=2,3,\cdots \]

Calcoliamo quindi il seguente sviluppo

\[ \begin{array}{l} \displaystyle (x+B+1)^{p+1} – (x+B)^{p+1}= \\ \binom{p+1}{1}x^{p}[(B+1)-B]+ \binom{p+1}{2}x^{p-1}[(B+1)^{2}-B^{2}] + \\ \binom{p+1}{3}x^{p-2}[(B+1)^{3}-B^{3}]+ \cdots \end{array} \]

Tenendo conto della relazione dei numeri di Bernoulli \((B+1)^{n}=B^{n}\) per \( n \gt 1\), abbiamo

\[ \begin{array}{l} (p+1)x^{p}=(x+B+1)^{p+1} – (x+B)^{p+1}= \binom{p+1}{1}x^{p} \end{array} \]

Assegnando a \(x\) i valori \(x=0,1,2,\cdots, n-1\) abbiamo

\[ \begin{array}{l} (p+1)\cdot 0= (1+B)^{p+1} – (B)^{p+1} \\ (p+1)\cdot 1^{p}= (2+B)^{p+1} – (1+B)^{p+1} \\ (p+1)\cdot 2^{p}= (3+B)^{p+1} – (2+B)^{p+1} \\ \vdots \\ (p+1)\cdot (n-1)^{p}= (n+B)^{p+1} – (n-1+B)^{p+1} \\ \end{array} \]

Sommando abbiamo

\[ \begin{array}{l} 1^{p}+ 2^{p}+ \cdots + (n-1)^{p} = \dfrac{(n+B)^{p+1} – B^{p+1}}{p+1} \end{array} \]

Esercizio 3.6
Dimostrare che, se consideriamo la somma di \(n\) termini, allora vale la stessa formula

\[ \begin{array}{l} 1^{p}+ 2^{p}+ \cdots + n^{p} = \dfrac{(n+B)^{p+1} – B^{p+1}}{p+1} \end{array} \]

dove tuttavia si deve intendere \(B_{1}=\dfrac{1}{2}\) invece di \(B_{1}=-\dfrac{1}{2}\).

4) I polinomi di Bernoulli

I polinomi di Bernoulli sono una successione di polinomi

\[ \{B_{k}(y),\ k=0,1,2,\cdots\} \]

definiti tramite il seguente sviluppo in serie di Taylor-Maclaurin:

\[ \frac{xe^{xy}}{e^{x}-1}=\sum\limits_{k=0} ^{\infty}\frac{B_{k}(y)x^{k}}{k!} \]

Dalla definizione abbiamo la relazione con i numeri di Bernoulli:

\[ B_{k}=B_{k}(0) \]

Con un ragionamento simile a quello del teorema 3.2 si dimostra la seguente proprietà:

Teorema 4.1

\[ B_{k}(y)= \sum\limits_{i=0}^{k}\binom{k}{i}B_{i}y^{k-i}=y^{k}+\binom{k}{1}x^{k-1}B_{1}+ \binom{k}{2}x^{k-2}B_{2}+ \cdots + \binom{k}{k}B_{k} \]

Dimostrazione
Calcolare il prodotto delle due serie:

\[ \frac{xe^{xy}}{e^{x}-1}=\sum\limits_{k=0} ^{\infty}\frac{B_{k}x^{k}}{k!} \cdot \sum\limits_{k=0} ^{\infty}\frac{(xy)^{k}}{k!} = \sum\limits_{k=0} ^{\infty} \left(\sum\limits_{i+j=k} ^{}\frac{B_{i}y^{j}}{i!j!}\right) x^{k} \]

Ricordare che \(\displaystyle\binom{k}{i}=\frac{k!}{i!(k-i)!}\).

I primi polinomi di Bernoulli sono i seguenti:

\[ \begin{array}{l} B_{0}(y)= 1 \\ B_{1}(y)= y -\frac{1}{2} \\ B_{2}(y)= y^{2} – y + \frac{1}{6} \\ B_{3}(y)= y^{3} -\frac{3}{2}y^{2} + \frac{y}{2} \\ B_{4}(y)= y^{4} -2y^{3} +y^{2} -\frac{1}{30} \\ \end{array} \]

Dalle formule per i casi iniziali con \(k=1,2,3,4\), Bernoulli derivò questa proprietà generale:

Teorema 4.1 – Bernoulli
Per ogni intero positivo \(k\) esiste un unico polinomio monico \(B_{k}(y)\) di grado \(k\) tale che

\[ s_{k}(n)= 1^{k}+2^{k}+ \cdots + (n-1)^{k}= \int\limits_{0}^{n}B_{k}(y) \]

Esercizio 4.1
Dimostrare la seguente relazione fra i polinomi di Bernoulli:

\[ B_{k}'(y)= kB_{k-1}(y) \]

Esercizio 4.2
Dimostrare la seguente relazione fra i polinomi di Bernoulli:

\[ B_{k}(y)= (-1)^{k}B_{k}(1-y) \]

Esercizio 4.3
Dimostrare la seguente relazione fra i polinomi di Bernoulli:

\[ \int\limits_{0}^{1}B_{k}(y)dy=0 \ ,\quad k \ge 1 \]

Esercizio 4.4
Dimostrare la seguente relazione fra i polinomi di Bernoulli:

\[ \begin{array}{l} B_{k}(y+1)-B_{k}(y)=ky^{k-1} \\ \int\limits_{y}^{y+1}B_{k}(t)dt=y^{k} \end{array} \]

Esercizio 4.5
Dimostrare la formula

\[ s_{k}(n)= \frac{1}{k+1} (B_{k+1}(n) – B_{k+1}(0)= \frac{1}{k+1} (B_{k+1}(n) – B_{k+1}) \]

Mettendo insieme il risultato dell’esercizio precedente e il teorema 4.1 ritroviamo la formula di Bernoulli per il calcolo di \(s_{k}(n)\).

Per approfondire lo studio dei numeri e dei polinomi di Bernoulli vedere ^[3].

Conclusione

Il metodo di Pascal per il calcolo delle somme di potenze di interi positivi, oltre a risolvere il problema specifico, introduce importanti connessioni fra la matematica discreta e la matematica del continuo, come il calcolo degli integrali e quindi delle aree. Anche la sua idea di introdurre una somma che presenta un comportamento telescopico è uno strumento molto potente utilizzato spesso nelle dimostrazioni.
Il metodo di Bernoulli fornisce una formula chiusa generale che introduce i cosiddetti numeri di Bernoulli, che trovano applicazioni in molti settori della matematica. In articoli successivi incontreremo nuovamente i numeri di Bernoulli, in particolare nel calcolo dei valori della funzione zeta di Riemann.

---

Bibliografia

^[1]A.W.F. Edwards – Pascal’s Arithmetical Triangle: The Story of a Mathematical Idea (Dover)

^[2]C. B. Boyer – Scripta Mathematica 9 (1943)

^[3]M. Spiegel – Schaum’s Outline of Calculus of Finite Differences and Difference Equations (McGraw-Hill)