In questo articolo studieremo il classico problema dell’inseguimento (pursuit problem), le cui origini sono molto antiche. Lo stesso Leonardo da Vinci ne fece i primi studi. Si tratta di un problema molto frequente nella programmazione dei videogiochi, ma anche in settori applicativi, come l’intercettazione di un missile o di un sommergibile. In questo articolo ci limiteremo al caso semplice di moto lineare della preda.
1) Achille e la tartaruga
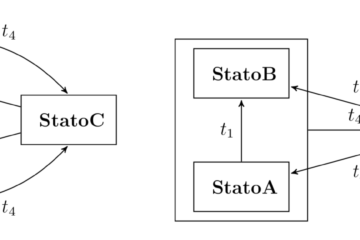
Dal punto di vista filosofico e matematico è interessante ricordare il famoso paradosso di Zenone, filosofo greco del V secolo a.C. Achille gareggia in una corsa con una tartaruga, concedendole un certo vantaggio iniziale. Secondo Zenone, nel tempo che Achille impiega per raggiungere il punto di partenza della tartaruga, quest’ultima si è sposata di un tratto, pur piccolo data la sua minore velocità. A questo punto, ripetendo il ragionamento, Zenone conclude che la tartaruga avrà sempre un piccolo vantaggio, per cui Achille non potrà mai raggiungerla. Il seguente diagramma illustra la situazione:
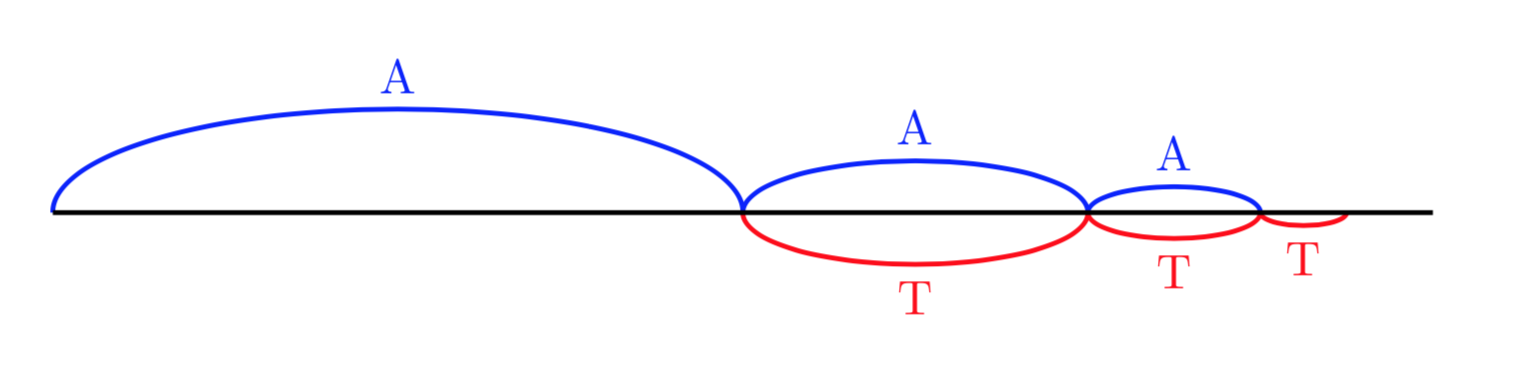
Naturalmente oggi possiamo risolvere facilmente il paradosso, in quanto sappiamo che la somma di un numero infinito di segmenti può avere lunghezza finita e quindi può essere percorsa in un tempo finito.
Esempio numerico del paradosso di Zenone
Supponiamo che la gara consista nel correre lungo un tratto rettilineo. Achille si muove alla velocità costante di \(10\) metri al secondo, mentre la tartaruga si muove con un decimo della velocità di Achille. La tartaruga parte con un vantaggio di \(100\) metri.
Achille deve raggiungere infiniti punti dove la tartaruga è già passata prima di raggiungerla, quindi sembrerebbe che resterà sempre indietro. In modo equivalente Achille deve percorrere un numero infinito di distanze prima di raggiungere la tartaruga.
Il tempo \(T\) necessario ad Achille per raggiungere i punti dove è arrivata la tartaruga può essere espresso in questo modo:
Si tratta di una serie infinita di tempi da sommare. Naturalmente oggi sappiamo che la somma di una serie infinita può essere finita. In questo caso abbiamo una serie geometrica convergente la cui somma è la seguente:
\[ T = 11 + \frac{1}{10}\frac{1}{1-\frac{1}{10}}= 11 + \frac{1}{9} \]Quindi Achille raggiungerà la tartaruga in meno di \(12\) secondi. Il punto debole del paradosso di Zenone era dovuto al fatto che al suo tempo si riteneva che la somma di infiniti numeri positivi dovesse essere sempre infinita.
Nonostante l’apparente semplicità della soluzione, non si deve sottovalutare il genio di Zenone e l’importanza del paradosso di Achille e la tartaruga, come di altri paradossi di Zenone (ad esempio il paradosso della freccia). Si tratta di esempi sofisticati che coinvolgono problemi matematici e filosofici fondamentali: la natura continua o discreta del tempo e dello spazio, la velocità istantanea di un corpo, la somma di un numero infinito di numeri, ecc.
I problemi posti da Zenone hanno richiesto lo sforzo dei migliori matematici per essere chiariti, a partire da Newton e Leibniz con la scoperta del calcolo differenziale e integrale. In seguito hanno portato alla definizione rigorosa del concetto di limite di una successione e di somma di una serie infinita.
2) Il problema generale dell’inseguimento
La prima trattazione matematica del problema dell’inseguimento può essere attribuita al matematico francese Pierre Bouguer (1698-1758) che risolse il problema lineare in due dimensioni. Bouguer studiò in particolare l’esempio di una nave di pirati che insegue un mercantile.
Nel caso generale il problema dell’inseguimento può essere così formulato: un punto \(P\) traccia una curva \(C_{1}\) mentre si muove mantenendo la sua direzione sempre verso la posizione di un punto \(Q\), che percorre una curva \(C_{2}\). Si assume che le velocità abbiano un rapporto costante \(k\). Il problema consiste nel determinare curva di inseguimento \(C_{1}\), una volta conosciuta la curva \(C_{2}\) e le due velocità.
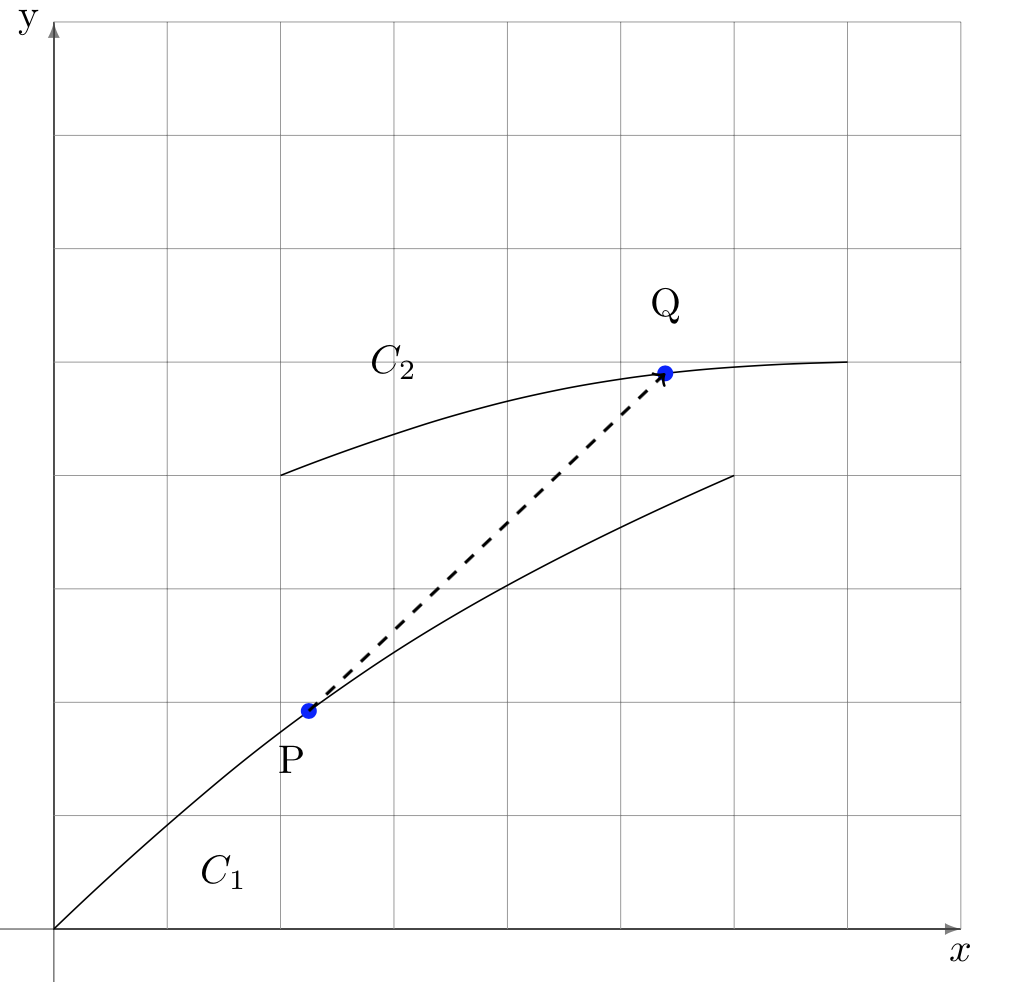
Indichiamo con \(P(x,y)\) un punto della curva \(C_{1}\) dell’inseguitore (il predatore), e con \(Q(X,Y)\) un punto della curva \(C_{2}\) dell’inseguito (la preda). L’equazione della curva \(C_{2}\) può essere scritta in forma implicita: \(f(X,Y)=0\). La tangente in \(P\) che passa attraverso un punto \(Q\) ha la seguente equazione differenziale:
\[ Y – y = \frac{dy}{dx}(X-x) \]Derivando queste equazioni abbiamo:
\[ \begin{array}{l} \dfrac{\partial f}{\partial X}\dfrac{dX}{dx} + \dfrac{\partial f}{\partial Y}\dfrac{dY}{dx} =0 \\ \dfrac{dY}{dx}=\dfrac{d^{2}y}{dx^{2}}(X-x)+ \dfrac{dy}{dx}\dfrac{dX}{dx} \end{array} \]Supponendo ora costante il rapporto delle velocità, cioè \( \dfrac{v_{P}}{v_{Q}}=k\), abbiamo
\[ dx^{2}+dy^{2}=k^{2}(dX^{2}+dY^{2}) \]Possiamo trattare \(x\) come unica variabile indipendente e ottenere la seguente equazione:
\[ \left(\dfrac{dy}{dx}\right)^{2}+1 = k^{2}\left[\left(\dfrac{dX}{dx}\right)^{2}+\left(\dfrac{dY}{dx}\right)^{2}\right] \]Mediante queste equazioni possiamo esprimere \(\dfrac{dX}{dx}\) e \(\dfrac{dY}{dx}\) come funzioni di \(x,y,\dfrac{dy}{dx},\dfrac{d^{2}y}{dx^{2}}\) e quindi trovare l’equazione differenziale non lineare della curva.
Tranne in casi molto particolari, non è possibile determinare la soluzione in forma chiusa di equazioni differenziali non lineari. Si deve ricorrere ad algoritmi di analisi numerica eseguiti su computer che calcolano soluzioni approssimate.
Per uno studio approfondito delle equazioni differenziali non lineari vedere [1].
3) Il caso lineare
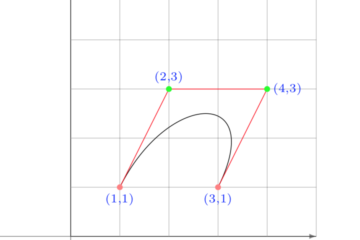
Consideriamo il caso più semplice, cioè quando la curva \(C_{2}\) è una linea retta. Per facilitare i calcoli supponiamo che la preda si muova nella direzione verticale di equazione \(X=a\).
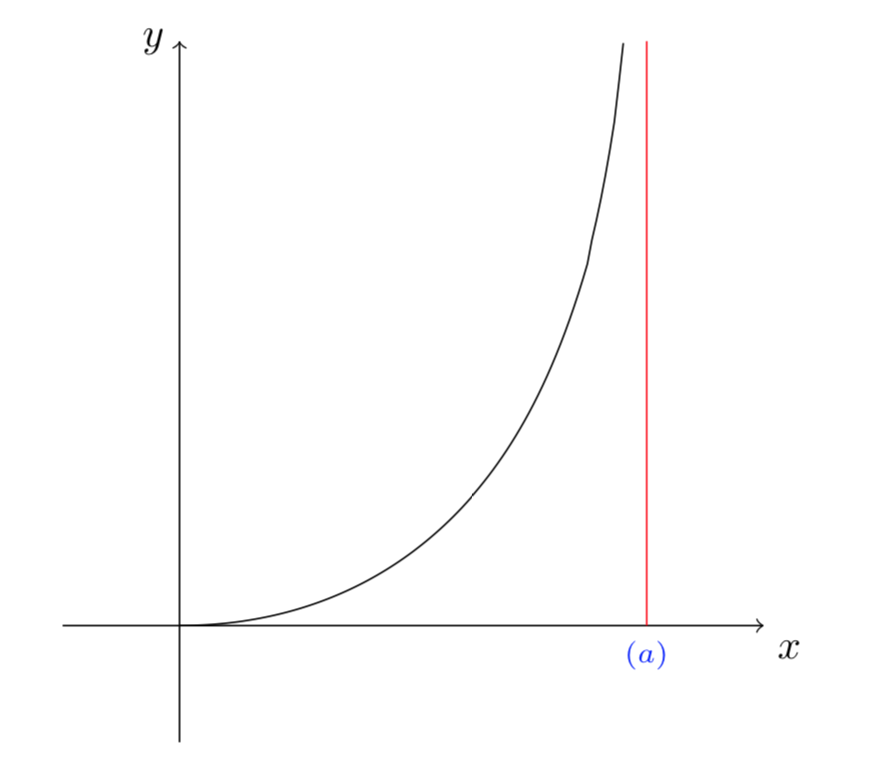
Le equazioni diventano più semplici:
\[ \frac{dY}{dx}=\frac{d^{2}y}{dx^{2}}(a-x) \] \[ 1+ \left(\frac{dy}{dx}\right)^{2}=k^{2}(a-x)^{2}\left(\frac{d^{2}y}{dx^{2}}\right)^{2} \]Se poniamo \(p=\dfrac{dy}{dx}\), abbiamo la seguente equazione
\[ \frac{kdp}{\sqrt{1+p^{2}}}=\frac{dx}{a-x} \]Questa equazione è a variabili separabili e può essere integrata facilmente:
\[ \ln \left(p+\sqrt{1+p^{2}}\right)=-\frac{1}{k}\ln(a-x) + C \]Effettuando dei calcoli algebrici possiamo possiamo calcolare l’espressione per la funzione \(p\):
\[ p=\frac{dy}{dx}=\frac{1}{2}\left[C_{1}(a-x)^{-\frac{1}{k}} – \frac{1}{C_{1}}(a-x)^{\frac{1}{k}}\right] \]dove \(C_{1}\) è una costante arbitraria.
Esaminiamo ora due casi distinti dipendenti dal valore di \(k\). Supponiamo prima che \(k \neq 1\). Integrando di nuovo abbiamo:
In base alle condizioni iniziali \(p=\dfrac{dy}{dx}=0\) quando \(x=0\), e quindi possiamo determinare i valori delle due costanti:
\[ C_{1}=a^{\frac{1}{k}}, C_{2}=\frac{ka}{k^{2}-1} \]Analizziamo ora il caso \(k=1\). Risolvendo l’equazione differenziale otteniamo la seguente soluzione:
\[ y=\frac{a}{4}\left[\left(1-\frac{x}{a}\right)^{2}-\ln \left(1-\frac{x}{a}\right)^{2}-1\right] \]Affinché sia possibile la cattura deve essere \( k \gt 1\), cioè il predatore deve avere una velocità maggiore della preda. Il punto di cattura si può determinare calcolando il punto di intersezione della traiettoria del predatore e della preda. Ponendo \(X=a\), troviamo le seguenti coordinate:
\[ \text{Punto di cattura: } \left(a,\frac{ka}{k^{2}-1}\right) \quad k \gt 1 \]Nel caso \(k=1\) la curva del predatore è asintotica alla linea retta della preda, e quindi il punto di cattura è all’infinito.
4) Distanza costante fra preda e predatore
Supponiamo ora di sostituire la condizione sul rapporto costante delle velocità, con la condizione che la distanza fra i due punti P,Q sia costante. Possiamo scrivere
\[ (Y-y)^{2}+ (X-x)^{2}= d^{2} \]Se poniamo \(X=d\) dalle equazioni precedenti abbiamo
\[ (Y – y)^{2} = \left(\frac{dy}{dx}\right)^{2}(d-x)^{2} \]Da queste due equazioni troviamo la seguente equazione differenziale della curva di inseguimento:
\[ \left(\frac{dy}{dx}\right)^{2}= \frac{d^{2}}{(d-x)^{2}} -1 \]La soluzione di questa equazione differenziale può essere trovata facilmente:
\[ y=-\sqrt{d^{2}-(d-x)^{2}}+d \cdot \ln \left[\frac{d+\sqrt{d^{2}-(d-x)^{2}}}{d-x}\right] + c \]La costante \(c\) è uguale a zero, in quanto \(y=0\) se \(x=0\).
Ricordiamo ora la definizione di alcune funzioni iperboliche:
\[ \begin{array}{l} \sinh (x) = \dfrac{e^{x}- e^{-x}}{2} \\ \cosh (x) = \dfrac{e^{x}+e^{-x}}{2} \\ \text{sech(x)}=\dfrac{1}{\cosh (x)}=\dfrac{2}{e^{x}+e^{-x}} \\ \end{array} \]L’inversa della secante è \(\text{arcsech(x)} = \ln\left(\dfrac{1+\sqrt{1-x^{2}}}{x}\right)\), definita nell’intervallo \((0,1]\).
L’equazione della curva di inseguimento può essere messa nella forma seguente:
\[ y=-\sqrt{d^{2}-(d-x)^{2}}+d \cdot \text{arcsech}\left(1-\frac{x}{d}\right) \\ \]In questa forma si riconosce l’equazione della trattrice.
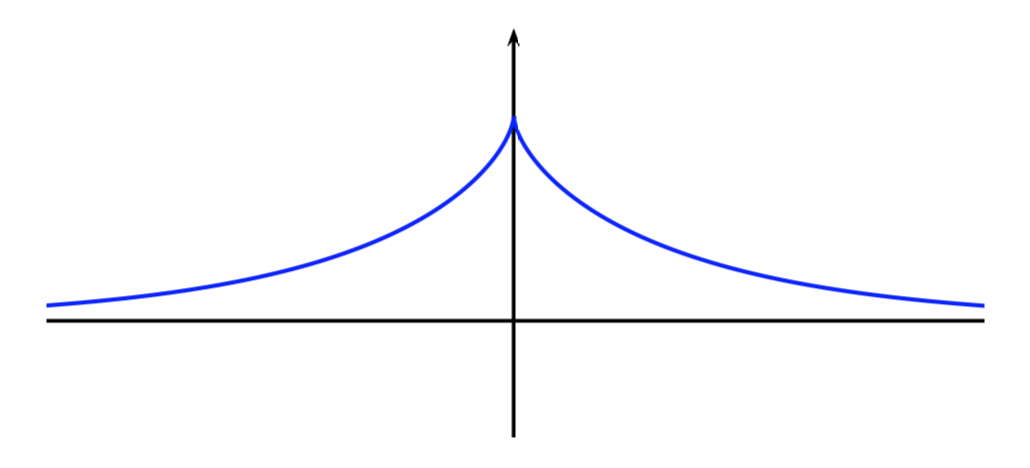
Una proprietà che caratterizza la trattrice è che per essa risulta di lunghezza costante il segmento di tangente tracciato dal punto di contatto con la curva al punto di intersezione con una data retta (chiamata retta base). L’equazione venne trovata da Leibniz nel 1693, mentre risolveva il seguente problema posto da Claude Perrault:
Quale è la curva descritta in un piano da un punto pesante \(P\) attaccato all’estremità di un filo teso, mentre l’altro estremo del filo si muove lungo una retta situata nello stesso piano?
Il nome trattrice venne dato da Huygens (1629-1695).
La curva trattrice è anche chiamata curva del cane, in quanto possiamo associare il punto \(P\) ad un cane, il filo teso al guinzaglio che il padrone del cane tiene nell’altra estremità, mentre si muove in linea retta.
Tra le diverse applicazioni matematiche della curva trattrice ricordiamo in particolare la creazione di modelli tridimensionali della geometria non-euclidea iperbolica di Lobachevsky (1792-1856): la superficie di rivoluzione della trattrice intorno al suo asintoto è la famosa pseudosfera di Beltrami (1835-1900), che ha una curvatura negativa, a differenza della sfera ordinaria che possiede una curvatura positiva.
5) Applicazione nei videogiochi in Unity 2D
Molti videogiochi, come Pac-Man, contengono esempi di inseguimento fra player e nemici. Il caso lineare nel quale il rapporto delle velocità è costante è naturalmente molto semplice. Può essere simulato aggiornando periodicamente la direzione del predatore in base alla posizione della preda.

Vector2 direction = (target.transform.position -
transform.position).normalized;
predatorRigidbody2D.MovePosition(
new Vector2(transform.position.x,transform.position.y)
+ direction * speed * Time.deltaTime);Nel caso in cui la velocità della preda è variabile il problema è più complesso. In questo caso muoversi costantemente con la direzione verso la posizione corrente della preda non è sufficiente. È necessario prevedere la posizione futura e aggiustare di conseguenza la direzione di inseguimento.
Un algoritmo importante è quello proposto da Craig Reynolds, all’inizio del 1990. Si tratta di un algoritmo dinamico che tiene conto sia della posizione sia della velocità corrente della preda. Sulle piccole distanze assume che la preda continuerà a muoversi con la stessa velocità del momento, e quindi calcola la nuova posizione. Per studiare l’algoritmo di Craig vedere [2] .
Conclusione
In questo articolo abbiamo analizzato il problema dell’inseguimento nel caso più semplice. Nonostante la complessità delle equazioni, è necessario che i programmatori applicativi di videogiochi acquisiscano una sufficiente conoscenza della matematica dell’inseguimento. In un prossimo articolo studieremo il problema dell’inseguimento nel caso in cui la preda si muove lungo una traiettoria circolare.
Bibliografia
[1]R. Enns – It’s a Nonlinear World (Springer)
[2]I. Millington – AI for Games (CRC Press)
0 commenti