La geometria delle curve e delle superfici ha una importanza fondamentale nella computer graphics in generale e nella programmazione dei videogiochi in particolare. In questo articolo descriveremo la matematica delle curve di interpolazione, in particolare delle spline e delle curve di Bézier con esempi di utilizzo nell’ambiente Unity.
1) Rappresentazione delle curve
1.1) Definizione matematica
Una curva è una funzione \(p: (a,b) \to \mathbb{R^{3}}\) da un intervallo della retta reale allo spazio \(\mathbb{R^{3}}\). La funzione \(p(t)\) è una funzione vettoriale con componenti \((x(t),y(t),z(t))\). La curva si dice differenziabile in un punto se nel punto sono differenziabili le tre funzioni componenti. Una curva differenziabile si dice regolare in un intervallo se in ogni punto esiste il vettore tangente.
In fisica una curva può rappresentare la traiettoria percorsa da una particella e il parametro \(t\) rappresenta il tempo. Il vettore ottenuto facendo le derivate delle tre componenti è il vettore tangente o vettore velocità.
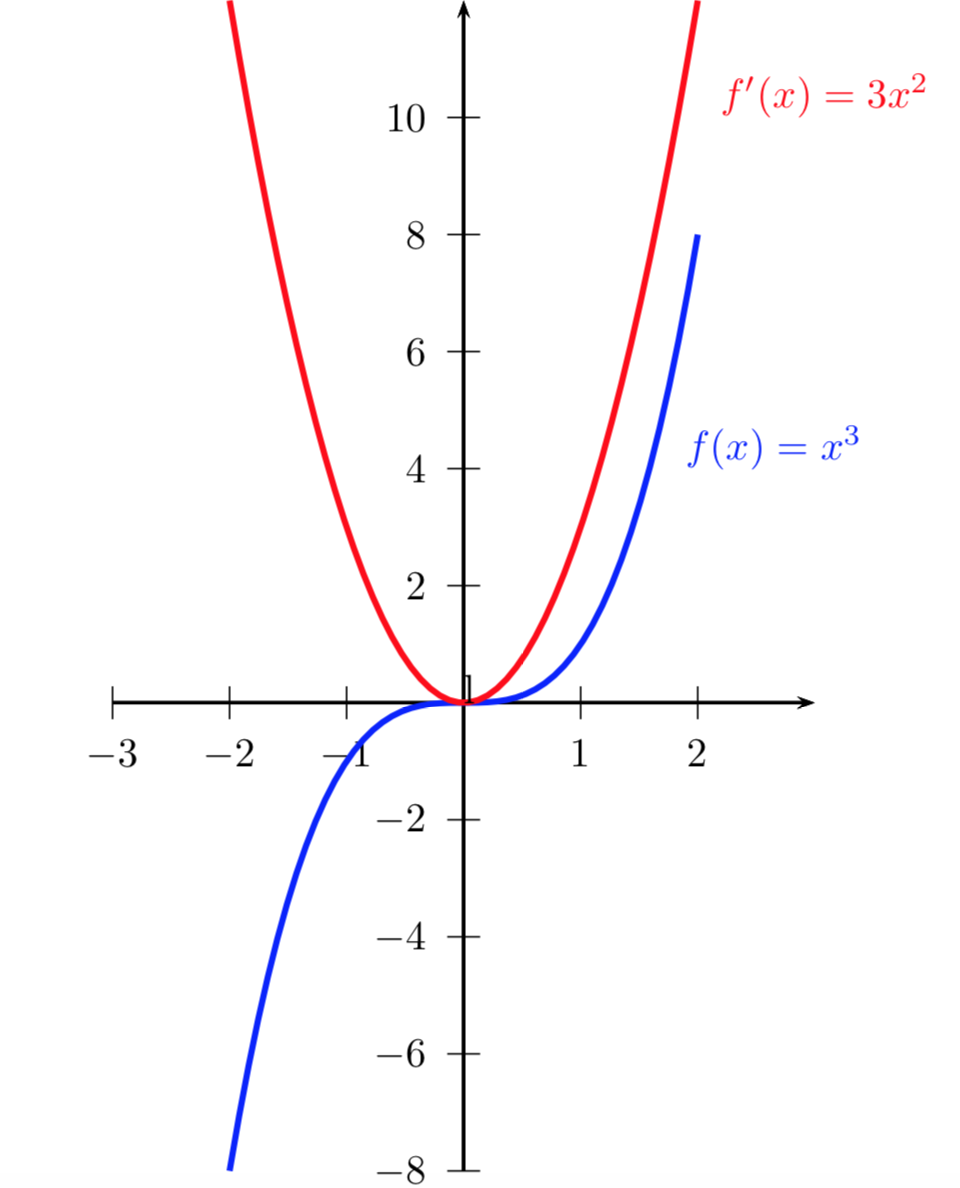
Esistono diversi tipi di rappresentazioni di una curva.
a) Rappresentazione esplicita di una curva nel piano
\[ y = f(x) \]Esempio 1.1
\[ \begin{split} y &=mx+b \quad \text{retta} \\ y &=\sqrt {\left(r^{2} – x^{2}\right)} \quad \text{circonferenza} \\ y &= x^{2} \quad \text{parabola} \end{split} \]b) Rappresentazione implicita
\[ F(x,y) = 0 \]Esempio 1.2
\[ \begin{split} ax+by+c &=0 \quad \text{ retta} \\ x^{2}+y^{2}-r^{2} &=0 \quad \text{circonferenza} \\ \end{split} \]c) Rappresentazione parametrica
In questo tipo una curva viene rappresentata mediante una variabile indipendente t, chiamata parametro.
Esempio 1.3 – La circonferenza
\[ \begin{split} x &= a \cos(t) \\ y &= a \sin (t) \\ \end{split} \]Esempio 1.4 – Elica circolare nello spazio
\[ \begin{split} x(t) &= a \cos (t) \\ y(t) &= a \sin (t) \\ z(t) &= bt \end{split} \]2) Curve parametriche polinomiali
La rappresentazione comune per le curve è la forma parametrica composta, costituita da vari tratti di curve che si raccordano agli estremi. Una curva parametrica polinomiale di grado \(n\) è rappresentata nella seguente forma:
\[ p(t) = \sum_{k=0}^{n}{a_{k}t^{k}} \]dove \(p(t)\) e \(a_{k}\) sono delle grandezze vettoriali:
\[ p(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \\ \end{pmatrix} \] \[ a_{k} = \begin{pmatrix} a_{kx} \\ a_{ky} \\ a_{kz} \\ \end{pmatrix} \]Esempio 2.1 – La retta parametrica
Dati due punti del piano o del spazio rappresentati dai vettori posizione \(p_{1}\) e \(p_{2}\), l’equazione della retta che passa per i due punti è la seguente:
Si tratta di una equazione vettoriale, che può essere proiettata nei tre assi cartesiani dando luogo ad un sistema di tre equazioni scalari:
\[ \begin{split} x(t) = x_{1} + (x_{2}-x_{1})t \\ y(t) = y_{1} + (y_{2}-y_{1})t \\ z(t) = z_{1} + (z_{2}-z_{1})t \\ \end{split} \]2.1) Curve parametriche del terzo ordine
Uno degli utilizzi principali delle curve è la rappresentazione del moto di oggetti nello spazio. I tipi di moti che si possono simulare dipendono dalla scelta del grado del polinomio. Con i polinomi di primo grado possiamo rappresentare solo movimenti rettilinei. Con i polinomi di grado \(2\) abbiamo un vasto spettro di movimenti possibili; tuttavia si tratta sempre di movimenti vincolati a rimanere in un piano. Per questi motivi nella computer graphics vengono utilizzate prevalentemente le curve parametriche di terzo ordine o grado, che permettono di rappresentare la quasi totalità dei movimenti. Utilizzare curve di grado maggiore darebbe pochi vantaggi e al contrario complicherebbe i calcoli e aumenterebbe i costi e tempi di elaborazione.
Una curva parametrica del terzo ordine ha la seguente equazione:
Si tratta di una equazione vettoriale, che in forma matriciale può essere scritta nel seguente modo:
\[ p(t)= \begin{pmatrix} a_{0x} & a_{1x} & a_{2x} & a_{3x} \\ a_{0y} & a_{1y} & a_{2y} & a_{3y} \\ a_{0z} & a_{1z} & a_{2z} & a_{3z} \\ \end{pmatrix} \cdot \begin{pmatrix} 1 \\ t \\ t^{2} \\ t^{3} \\ \end{pmatrix} \]2.2) Continuità parametrica e geometrica
In genere si utilizzano curve composte da varie componenti curvilinee separate. Ogni curva componente è continua ovunque nel suo intervallo di definizione, ma interessa studiare la continuità anche nei punti di giunzione. Per questo vengono definiti due tipi di continuità per le curve parametriche: la continuità geometrica e la continuità parametrica.
Un punto di giunzione fra due segmenti di una curva parametrica si dice che ha continuità parametrica di classe \(C^{0}\) se i valori dei due segmenti di curve coincidono nel punto. Un punto di giunzione fra due segmenti si dice continuo di classe \(C^{1}\) se i valori dei due segmenti coincidono e anche i valori delle derivate prime \(\frac{dx}{dt}, \frac{dy}{dt},\frac{dz}{dt}\) coincidono. In modo simile si definisce la continuità parametrica di classe \(C^{k}\).
Un punto di giunzione fra due componenti si dice che ha continuità geometrica di classe \(G^{0}\) se i valori dei due segmenti di curve coincidono nel punto. Un punto di giunzione si dice continuo di classe \(G^{1}\) se i valori dei due segmenti coincidono e i valori delle derivate prime \(\frac{dx}{dt}, \frac{dy}{dt},\frac{dz}{dt}\) sono proporzionali. La cosa importante è che i vettori tangenti di entrambe le componenti abbiano la stessa direzione nel punto di collegamento. In modo simile si definisce la continuità geometrica di classe \(G^{k}\).
Naturalmente la continuità parametrica implica quella geometrica, ma non è vero il viceversa. Per comprendere meglio la differenza fra queste due definizioni, è utile immaginare la situazione fisica di una particella che si muove da un segmento di curva all’altro passando per il punto di giunzione. Nel caso della continuità parametrica il passaggio avviene in modo fluido, senza variazione della velocità, né in direzione né in grandezza. Nel caso della continuità geometrica invece, pur rimanendo invariata la direzione, c’è un cambiamento istantaneo del modulo della velocità, e quindi un’accelerazione, nel passaggio fra i due segmenti di curve.
3) Interpolazione polinomiale
Un’esigenza tipica nella computer graphic e nei videogiochi è quella di modellizzare oggetti complessi e di simulare processi di animazione, a partire da un insieme finito di dati di controllo. Gli strumenti matematici fondamentali per questi problemi sono le curve (o superfici) interpolanti o approssimanti. Con l’interpolazione la curva passa esattamente attraverso i punti specificati (ad esempio le spine naturali); con l’approssimazione passa soltanto attraverso i punti estremi e utilizza i punti intermedi come guida per la costruzione ottimale della curva (ad esempio le curve di Bezier).
- Le curve interpolanti interpolano i punti, cioè passano per questi; le curve approssimanti assumono una forma in funzione dei punti, ma non necessariamente passano attraverso di essi.
- Le curve interpolanti sono molto utili per specificare le traiettorie nei processi di animazione, in cui si vuole che la traiettoria di un oggetto passi nei punti.
- Le curve approssimanti sono molto utili nei processi di modellizzazione.
Possiamo formalizzare il problema dell’interpolazione polinomiale in queste due situazioni:
- dati \(n+1\) punti del piano \((x_{0},y_{0}),(x_{1},y_{1}), \cdots (x_{n},y_{n})\), determinare un polinomio \(p(x)\) di grado al massimo \(n\) che nei punti assume dei valori prefissati \(y_{i}\), cioè \(p(x_{i})=y_{i}, i=0,1, \cdots n\) ;
- data una funzione \(f(x)\) continua in un intervallo \([a,b]\), determinare il polinomio di grado \(n\) che approssima la funzione in modo ottimale.
I polinomi hanno importanti proprietà che li rendono strumenti ideali nei processi di interpolazione o approssimazione. Sono funzioni continue, facilmente derivabili e integrabili, e possono essere calcolati facilmente con semplici programmi. L’insieme dei polinomi di grado minore od uguale a \(n\) ha una struttura di spazio vettoriale. Per un ripasso della definizione e delle proprietà degli spazi vettoriali vedere [1].
I polinomi sono in grado di approssimare qualsiasi funzione continua con il livello di precisione desiderato; infatti il famoso Teorema di approssimazione di Weierstrass afferma sostanzialmente che ogni funzione continua in un intervallo chiuso e limitato può essere approssimata da polinomi con ogni livello di precisione desiderato.
3.1) Interpolazione di Lagrange
Supponiamo di avere \(n+1\) punti del piano
\[ (x_{0},y_{0}),(x_{1},y_{1}), \cdots ,(x_{n},y_{n}) \]Si tratta di determinare un polinomio \(p(x)\), di grado minimo, tale che \(p(x_{i})=y_{i}\) con \(0 \le i \le n\).
La soluzione proposta da Lagrange utilizza i seguenti polinomi \(L_{n,k}(x)\):
Esercizio 3.1
Dimostrare la seguente proprietà:
La soluzione di Lagrange è contenuta nel seguente teorema:
Teorema 3.2 – Lagrange
Esiste un unico polinomio di grado al massimo \(n\) che assume i valori \(y_{i}\) nei punti \(x_{i}\). Il polinomio è dato dalla seguente espressione:
L’errore varia da punto a punto. È zero nei punti di interpolazione, ed è diverso da zero negli altri punti. Per avere una stima dell’errore ricordiamo la seguente formula:
Teorema 3.3
Nella formula di Lagrange, per ogni \(x \in [a,b]\), esiste un numero \(\xi(x)\) che dipende da \(x\) tale che:
Il seguente esempio ottenuto con il prodotto SageMath illustra l’interpolazione di Lagrange per la funzione \(y=\cos (x)\), con \(n=3\), nell’intervallo \([0,2\pi]\).
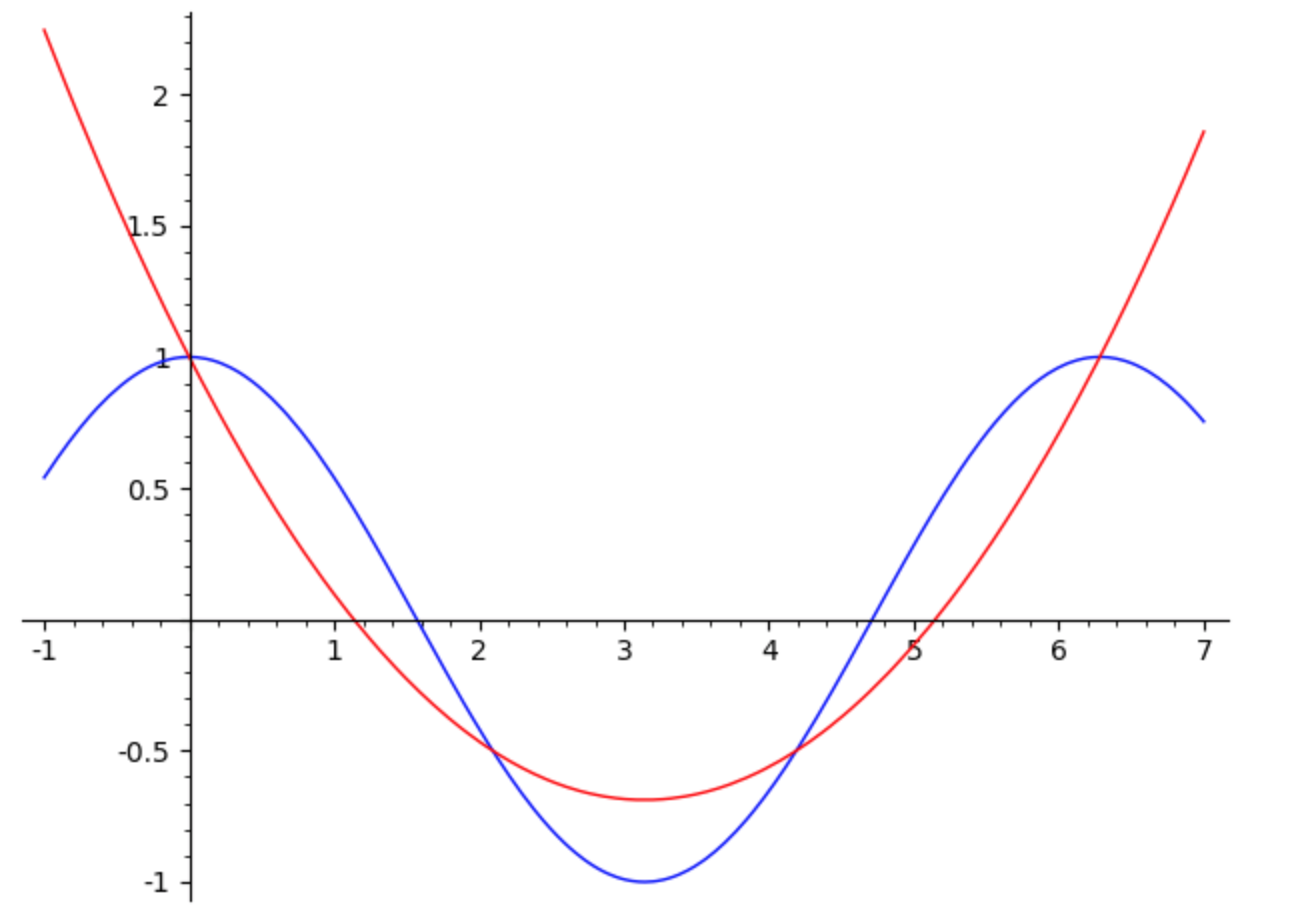
3.2) Interpolazione di Hermite
Lo scopo dell’interpolazione di Hermite è di migliorare l’approssimazione di Lagrange, imponendo la condizione ulteriore che anche le derivate assumano lo stesso valore nei punti di controllo.
Definizione
Sia \(f(x)\) una funzione con derivata prima continua nell’intervallo \([a,b]\), in simboli \(f \in C^{1}[a,b]\). Siano \((x_{0}, \cdots ,x_{n})\) punti distinti nell’intervallo \([a,b]\). Il polinomio interpolante di Hermite \(p(x)\) ha le seguenti proprietà:
Teorema 3.4 – Hermite
Sia data una funzione \(f(x)\) di classe \(C^{1}[a,b]\) e siano \((x_{0},x_{1}, \cdots ,x_{n})\) \(n+1\) punti distinti nell’intervallo di definizione. Allora esiste un unico polinomio interpolante di grado minore od uguale a \(2n+1\), dato dalla seguente espressione:
dove \(H_{n,i}(x)\) e \(K_{n,i}(x)\) sono dei polinomi collegati ai polinomi di Lagrange \(L_{n,i}(x)\). Il polinomio \(p(x)\) viene chiamato polinomio osculatore del primo ordine. Riportiamo senza dimostrazione le formule per i polinomi \(H_{n,i}(x)\) e \(K_{n,i}(x)\) .
\[ \begin{split} H_{n,i}(x)&=[1- 2(x-x_{i})L_{n,i}^{‘}(x_{i})](L_{n,i}(x))^{2} \\ K_{n,i}(x)&= (x-x_{i})(L_{n,i}(x))^{2} \end{split} \]Notiamo che nel caso di un singolo punto \(x_{0}\) il polinomio osculatore si riduce al polinomio di Taylor.
Per uno studio completo dell’interpolazione di Lagrange e di Hermite vedere [2] oppure [3].
4) Polinomi di Bernstein
L’insieme costituito da tutti i polinomi a coefficienti reali di grado minore o uguale a \(n\) ha una struttura di spazio vettoriale; i polinomi possono essere sommati fra loro e moltiplicati per una grandezza scalare.
Una base naturale per questo spazio vettoriale è costituita dai polinomi \(\{1,x,x^{2}, \cdots , x^{n}\}\). Ogni altro polinomio di grado \(\le n\) può essere espresso come combinazione lineare di polinomi della base. Tuttavia esistono altre basi possibili; una di queste è costituita dai polinomi di Bernstein che ora introdurremo.
Definizione 4.1
I polinomi di Bernstein di grado \(n\) sono così definiti:
Esistono \(n+1\) polinomi di Bernstein di grado \(n\). I polinomi di Bernstein di grado \(n\) formano una base per l’insieme dei polinomi.
I polinomi di grado \(1\) sono:
\[ \begin{split} B_{1,0}(t) &= 1-t \\ B_{1,1}(t) &= t \end{split} \]I polinomi di grado \(2\) sono:
\[ \begin{split} B_{2,0}(t) &= (1-t)^{2} \\ B_{2,1}(t) &= 2t(1-t) \\ B_{2,2}(t) &= t^{2} \\ \end{split} \]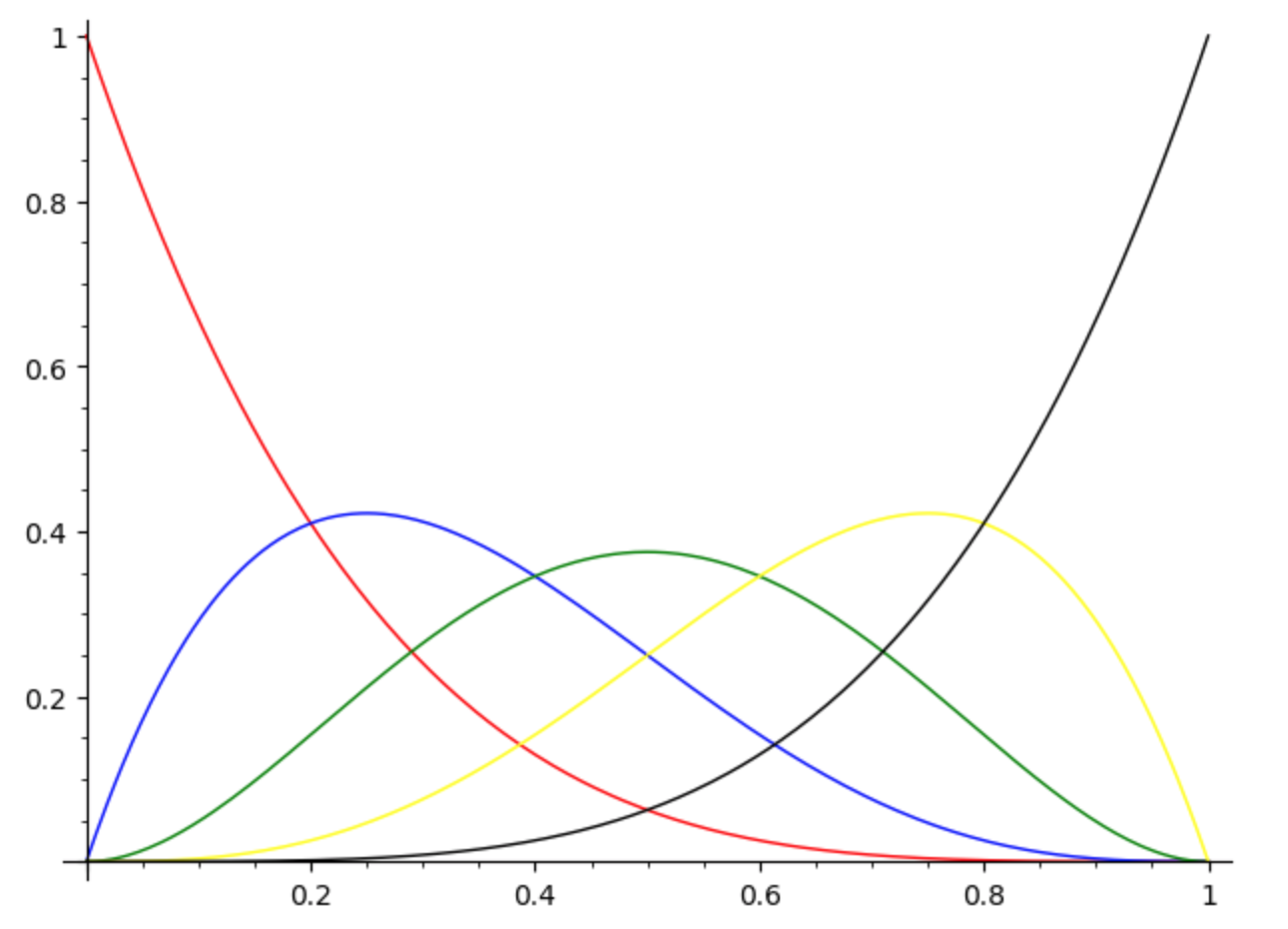
Dalla definizione, seguono facilmente le seguenti proprietà:
Teorema 4.1
\[ \begin{split} B_{n,k}(t) & \ge 0 \quad \text{\( \forall t\in [0,1]\)} \\ B_{n,k}(t) &=B_{n,n-k}(1-t) \\ B_{n,k}(t) &= (1-t)B_{n-1,k}(t) +tB_{n-1,k-1}(t)\\ \end{split} \]Esercizio 4.1
Dimostrare le seguenti formule:
I polinomi di Bernstein possono essere utilizzati per dimostrare il seguente famoso e importante teorema di Weierstrass (1815-1897):
Teorema 4.2 – Weierstrass
Sia \(f(x)\) una funzione continua nell’intervallo \([0,1]\). Allora per ogni fissato \(\epsilon >0\) esiste un polinomio \(p(x): [0,1] \to \mathbf{R}\) tale che
Possiamo formulare il teorema in una forma equivalente. Definiamo la funzione polinomiale di Bernstein:
\[ f_{n}(x) = \sum_{k=0}^{n} f\left(\frac{k}{n}\right) B_{n,k}(x) \]Allora la successione dei polinomi \(f_{n}(x)\) converge uniformemente alla funzione \(f(x)\) nel suo dominio di definizione \([0,1]\).
Per un approfondimento dei polinomi di Bernstein e la dimostrazione del teorema di Weierstrass vedere ad esempio [4].
5) Le spline
In molte applicazioni gli oggetti da rappresentare non sono definibili in modo preciso mediante curve semplici, come archi, ellissi, ecc. Le curve ( o anche le superfici) modellizzanti vengono spesso create a partire da un insieme di punti rappresentativi dell’oggetto. I punti e le direzioni delle tangenti in ogni punto solo utilizzati per determinare l’equazione del polinomio che approssima la forma della curva. La curva ottenuta che passa attraverso i punti si chiama spline interpolante.
Altri tipi di spline non passano attraverso tutti i punti; alcuni sono utilizzati per controllare e modellizzare la forma alla curva nelle vicinanze di ogni punto. La curva ottenuta si chiama spline approssimante.
Le spline più utilizzate sono quelle di terzo grado.
5.1) Spline cubica
Siano dati \(n+1\) punti o nodi \(\{x_{0},x_{1}, \cdots, x_{n}\}\), con \(x_{0} < x_{1} < \cdots < x_{n}\). Una funzione spline cubica di grado \(3\) è una funzione composita \(S_{3,n}(x)\) definita nell’intervallo contenente i punti nel seguente modo:
\[ S_{3,n}(x)= \begin{cases} p_{1}(x) \quad x \in [x_{0},x_{1}] \\ p_{2}(x) \quad x \in [x_{1},x_{2}] \\ \vdots \\ p_{n}(x) \quad x \in [x_{n-1},x_{n}] \\ \end{cases} \]Di fatto la funzione \(S_{3,n}(x)\) è una collezione costituita da \(n\) polinomi \(p_{i}(x)\) di grado al massimo \(3\).
Supponiamo ora di avere per ogni punto \(x_{i}\) un valore \(f({i})\). La spline \(S_{3,n}(x)\) si dice spline cubica interpolante rispetto alle coppie di dati \((x_{i},f_{i})\) se risulta:
Chiaramente all’interno di ogni intervallo \([x_{i-1},x_{i}]\) il polinomio \(p_{i}(x)\) ha derivate di tutti gli ordini. I punti di discontinuità della spline \(S_{3,n}(x)\) possono essere solo nei nodi. In genere si impongono ulteriori condizioni di continuità nei nodi:
\[ \begin{split} p_{i-1}(x_{i}) &= p_{i}(x_{i}) \\ p_{i}'(x_{i}) &= p_{i+1}'(x_{i}) \\ p_{i}’^\prime(x_{i}) &= p_{i+1}’^\prime(x_{i}) \\ \end{split} \]Possono essere definiti diversi tipi di curve spline, impostando diverse condizioni al contorno nei nodi. Per uno studio sistematico dei vari tipi di spline (naturale, completa e altri) e dello loro proprietà vedere il testo di Quarteroni della bibliografia.
Esercizio 5.1
Costruire la spline naturale del primo ordine per approssimare i seguenti dati: \((0,0),(1,2),(2,1),(3,0)\).
Soluzione
La curva ottenuta con lo strumento SageMath è la seguente:
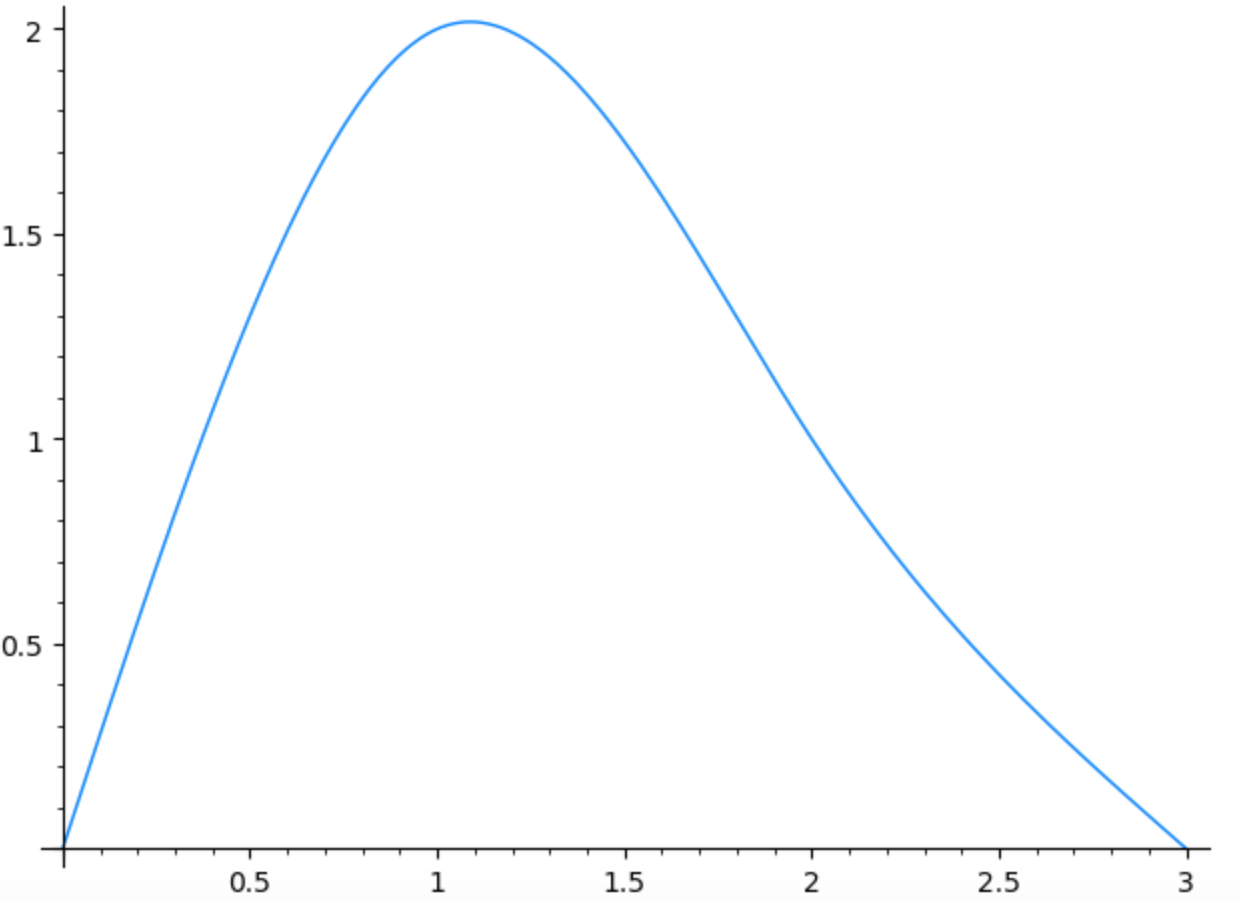
5.2) Spline cubica di Hermite
Una spline cubica di Hermite cerca di controllare la forma della curva mediante condizioni sulle tangenti nei punti estremi.
Definizione 5.2
Sia dato un intervallo \([a,b]\) e una funzione \(f: [a,b] \to\mathbf{R} \) derivabile. Sia data una partizione dell’intervallo in \(n + 1\) punti: \(x_{0}, \cdots, x_{n}\). La spline cubica di Hermite è un insieme finito di polinomi \(p_{0}, \cdots,p_{n-1}\), che soddisfano le seguenti relazioni:
per \(i=0,1, \cdots, n-1\).
Di fatto ogni componente della spline cubica di Hermite ha la seguente rappresentazione:
\[ p(t)=H_{0}(t)p_{0}+ H_{1}(t)v_{0}+ H_{2}(t)v_{1}+ H_{3}(t)p_{1} \]dove \(p_{0},p_{1}\) sono i punti iniziale e finale, \(v_{0},v_{1}\) sono le tangenti nei punti, e i polinomi \(H_{i}(t)\) hanno la seguente espressione:
\[ \begin{split} H_{0}(t)&= (1+2t)(1-t)^{2} \\ H_{1}(t)&= t(1-t)^{2} \\ H_{2}(t)&= t^{2}(t-1) \\ H_{3}(t)&= t^{2}(3-2t) \\ \end{split} \]Si può dare una rappresentazione matriciale
\[ p(t) = \left( \begin{array}{cccc} p_{0} & v_{0} & v_{1} & p_{1} \end{array} \right) \cdot \left( \begin{array}{cccc} 1 & 0 & -3 & 2 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 3 & -2 \end{array} \right) \cdot \left( \begin{array}{c} 1 \\ t \\ t^{2} \\ t^{3} \end{array} \right) \\ \]oppure la seguente equivalente:
\[ p(t) = \left( \begin{array}{cccc} t^{3} & t^{2} & t & 1 \end{array} \right) \cdot \left( \begin{array}{cccc} 2 & -2 & 1 & 1 \\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{array} \right) \cdot \left( \begin{array}{c} p_{0} \\ p_{1} \\ v_{0} \\ v_{1} \end{array} \right) \\ \]Diversamente dalle curve di Bézier, la forma di Hermite di una curva non è una media pesata, in quanto la somma \(H_{0}+H_{1}+H_{2}+H_{3}\) non è in genere uguale a \(1\). I coefficienti \(H_{0},H_{3}\) sono i punti iniziale e finale, mentre i coefficienti \(H_{1},H_{2}\) sono vettori.
5.3) Le spline di Catmull-Rom
La spline di Hermite è semplice da calcolare e permette di costruire una curva composta fluida e dotata di simmetria. Per modificare la curva si può modificare la posizione di un nodo oppure la direzione della tangente nel nodo. Tuttavia ha lo svantaggio della necessità di conoscere le derivate nei nodi.
Nel caso in cui non si conoscono le derivate si possono approssimare le derivate con delle differenze finite. È questo l’approccio proposto da E. Catmull e R. Rom nel 1974[5].
Una delle caratteristiche della spline di Catmull-Rom è che la curva passa attraverso tutti i punti di controllo, diversamente da altri tipi di spline.
Come sappiamo la spline è una collezione di curve cubiche collegate fra loro nei punti estremi. La prima curva va dal punto \(p_{0}\) al punto \(p_{1}\). La seconda dal punto \(p_{1}\) al punto \(p_{2}\), ecc. Per avere continuità nei punti di collegamento delle curve è necessario che le due tangenti siano uguali. Il procedimento standard delle spline di Catmull-Rom crea la tangente in un punto utilizzando i punti vicini. La formula per la tangente \(\mathbf{v}_{i}\) nel punto \(p_{i}\) è la seguente:
Il fatto importante è che per calcolare la tangente in un punto basta conoscere la posizione dei punti adiacenti.
Il procedimento per determinare la spline di Catmull-Rom è simile a quello utilizzato per la spline di Hermite; la rappresentazione matriciale è la seguente:
6) Le curve di Bézier
Le curve di Bézier rappresentano una classe fondamentale di curve spline. Il nome deriva dal francese Pierre Bézier (1920-1999) che pubblicò per primo un articolo, mentre lavorava presso la casa automobilistica Renault come disegnatore e progettista. In realtà lo stesso tipo di curve era già stato studiato da Paul de Casteljau mentre lavorava alla Citroen, ma non pubblicò la sua ricerca.
Definizione 6.1
Siano dati \(n+1\) punti \(\{p_{0},p_{1}, \cdots , p_{n}\}\). La curva di Bézier è definita dalla seguente equazione:
dove \(B_{n,k}(t)\) sono i polinomi di Bernstein.
Le principali proprietà della curva di Bézier sono le seguenti:
- la curva passa nei punti iniziale e finale \(p_{0}\) e \(p_{1}\)
- la curva giace nelle regione convessa delimitata dai punti, in quanto \(B_{n,k}(t) \ge 0\), per ogni \(t \in [0,1]\)
- la curva è tangente nei punti estremi a \(p_{1}-p_{0}\) e \(p_{n}-p_{n-1}\)
Tali punti si dicono punti di controllo. La spezzata formata dai segmenti che li congiungono si chiama poligono di controllo. Soltanto il primo e l’ultimo punto di controllo appartengono alla curva di Bézier, mentre i restanti contribuiscono a modellizzare la curva nelle loro vicinanze. Si tratta quindi di una curva approssimante, e non di una curva interpolante.
I polinomi di Bernstein servono come funzioni di blending per le curve di Bézier, cioè come pesi associati ai punti di controllo. L’ordine del polinomio che rappresenta la curva è uguale al numero dei punti di controllo meno uno.
Uno svantaggio delle curve di Bézier è rappresentato dalla mancanza di controllo locale sulla curva. Se modifichiamo un punto di controllo, la curva intera viene modificata, e non solo la parte locale vicina al punto.
6.1) Curve cubiche di Bézier
Le curve di Bézier maggiormente utilizzate sono quelle di terzo grado, definite da quattro punti di controllo. In questo caso i polinomi di Bernstein sono i seguenti:
\[ \begin{split} B_{3,0}(t) &=(1-t)^{3} \\ B_{3,1}(t) &=3t(1-t)^{2} \\ B_{3,2}(t) &=3t^{2}(1-t) \\ B_{3,3}(t) &=t^{3} \\ \end{split} \]Esercizio 6.1
Dimostrare le seguenti relazioni soddisfatte dalla derivata prima della curva cubica di Bézier:
6.2) Rappresentazione matriciale delle cubiche di Bézier
La curva cubica di Bézier (caso \(n=3)\) con i \(4\) punti di controllo \(\{p_{0},p_{1},p_{2},p_{3}\}\), ha la seguente espressione vettoriale:
\[ p(t) = (1-t)^{3}p_{0}+3t(1-t)^{2}p_{1}+3t^{2}(1-t)p_{2}+t^{3}p_{3} \]In forma matriciale può essere scritta nel seguente modo:
\[ p(u) = \left( \begin{array}{cccc} t^{3} & t^{2} & t & 1 \end{array} \right) \cdot \frac{1}{2} \left( \begin{array}{cccc} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array} \right) \cdot \left( \begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ p_{3} \end{array} \right) \\ \]Esercizio 6.2
Disegnare la curva di Bézier relativa ai seguenti \(4\) punti:
Soluzione
La curva nel piano è rappresentata dalla seguente coppia di equazioni parametriche:
Il grafico della spline di Bézier è il seguente:
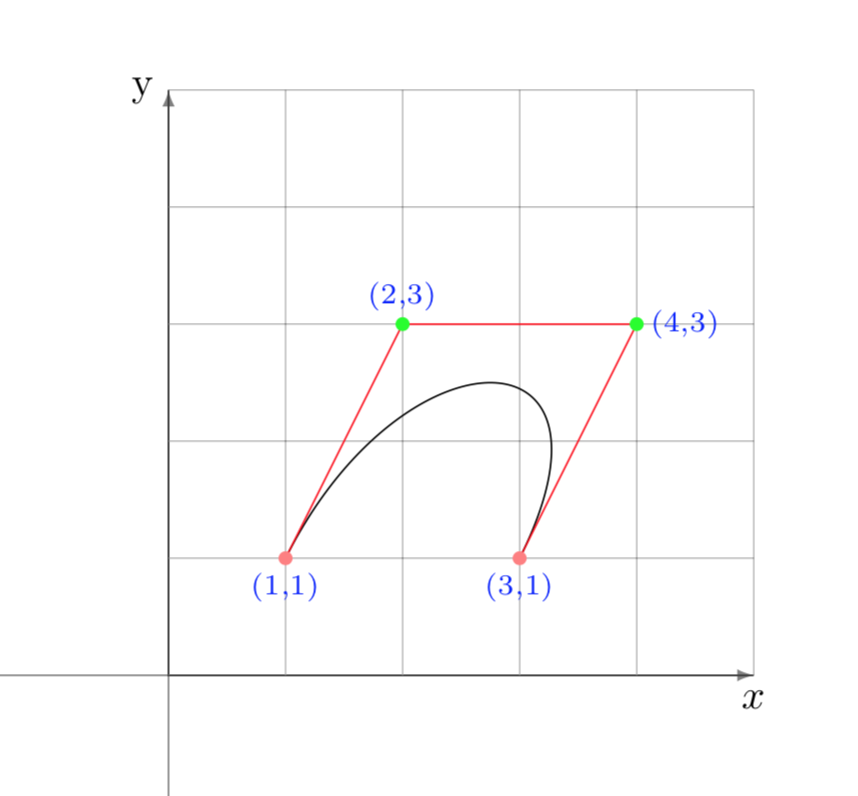
Il grafico è stato creato con il prodotto TikZ nell’ambiente Latex, mediante l’istruzione seguente:
\draw[scale=1,domain=0:1,samples=100,variable=\t]
plot ({(1-\t)^3 +6*\t*(1-\t)^2 +12*\t^2*(1-\t)+3*\t^3},
{(1-\t)^3 +9*\t*(1-\t)^2 +9*\t^2*(1-\t)+\t^3});Questo modo di calcolare la curva di Bézier va bene solo nel caso in cui si hanno pochi nodi. All’aumentare del numero dei nodi aumenta il grado del polinomio e si presentano instabilità numeriche ed errori di arrotondamento.
Un modo migliore è quello di utilizzare l’algoritmo di de Casteljau.
6.3) L’algoritmo di de Casteljau
Nel 1959 Paul de Casteljau (1910-1999) ha creato un algoritmo semplice ed efficiente che costruisce una curva di Bézier attraverso ripetute interpolazioni lineari. L’algoritmo inizia fissando un valore del parametro \(t \in(0,1)\). Fra ogni coppia di punti di controllo consecutivi viene fatta una interpolazione lineare in funzione del parametro \(t\), ottenendo un nuovo punto. Partendo dai \(4\) punti di controllo iniziali indicati con questa notazione: \((p_{0}^{0},p_{1}^{0},p_{2}^{0},p_{3}^{0})\), otteniamo \(3\) nuovi punti \((p_{0}^{1},p_{1}^{1},p_{2}^{1})\). Proseguiamo fino ad ottenere un solo punto \(p_{0}^{3}\) che è il valore cercato del polinomio in \(t\): \(p(t)\). In ogni passo dell’algoritmo viene creato un nuovo punto fra ogni coppia nel rapporto \(t:(1-t)\).
Possiamo riassumere l’algoritmo con queste equazioni di ricorrenza:
\[ \begin{split} p_{i}^{0}(t) &= p_{i} \\ p_{i}^{n}(t) &= (1-t) p_{i}^{n-1}(t) + tp_{i+1}^{n-1}(t) \end{split} \]Per vedere in azione l’algoritmo di de Casteljau consultare questo articolo di Wikipedia link.
7) Utilizzo delle curve di Bézier nei videogiochi
Le spline vengono utilizzate in varie situazioni nei videogiochi, tra le quali ad esempio:
- per controllare il movimento di un personaggio NPC (Non-Player Character), in modo che il suo moto risulti fluido e il più possibile realistico. Questo viene garantito dalla continuità delle derivate prima e seconda della spline;
- per descrivere differenti percorsi;
- per modellizzare oggetti di varie forme geometriche;
- nelle animazioni Unity per definire curve utili nella interpolazione dei keyframe (vedi articolo su questo sito link).
7.1) Generazione di una spline di Catmull-Rom
La spline di Catmull-Rom è utile per calcolare una curva che passi attraverso tutti i punti di controllo e abbia una forma curvilinea. Ad esempio può essere utilizzata per calcolare la curva di un oggetto a partire dai keyframes in un processo di animazione.
La seguente animazione illustra un oggetto che si muove attraverso \(5\) punti prefissati, seguendo una traiettoria curva creata con l’algoritmo di Catmull-Rom.

Le istruzioni per calcolare i punti della curva sono le seguenti:
// calcola la posizione sulla spline Catmull-Rom,
// relativa al parametro t
Vector3 CalcolaPosizioneCatmullRom(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
Vector3 posizione = 0.5f * (2*p1 + (p2-p0)*t +
(2*p0-5*p1+4*p2-p3)*t*t +
(-p0+3*p1-3*p2+p3)*t*t*t);
return posizione;
}7.2) Moto lungo una curva di Bézier
In alcune situazioni le curve di Bézier vengono utilizzate per definire un percorso, attraverso il quale si deve muovere un oggetto.
L’animazione seguente si riferisce ad un cammino a forma di farfalla, composto da \(4\) percorsi collegati nei punti di giunzione.
Ogni percorso viene realizzato mediante una curva di Bézier distinta, con \(4\) punti di controllo. Il quarto punto di controllo di ogni curva coincide con il primo della successiva. La funzione Update attiva una coroutine per calcolare i singoli percorsi, tramite la formula di Bézier:
private IEnumerator MotoSulPercorso(int numero) {
// p0,p1,p2,p3 sono i punti di controllo
..............
while (t < 1) {
t += Time.deltaTime * fattoreVelocita;
puntoCalcolato =
Mathf.Pow(1 - t, 3) * p0 +
3 * Mathf.Pow(1 - t, 2) * t * p1 +
3 * (1 - t) * Mathf.Pow(t, 2) * p2 +
Mathf.Pow(t, 3) * p3;
transform.position = puntoCalcolato;
yield return new WaitForEndOfFrame();
}
..............
}Modificando il numero delle curve componenti e cambiando le posizioni dei punti di controllo è possibile creare una infinità di curve diverse, che si possono adattare alle varie situazioni.
7.3) Velocità costante lungo una curva di Bézier
Il grafico di una curva \(p(t)=(x(t),y(t))\) può essere pensato come la traiettoria di una particella che si muove nel piano, e la \(p(t)\) indica la posizione al tempo \(t\). La velocità della particella è data dalla seguente equazione vettoriale:
\[ v(t) = \frac{dp}{dt} \]Indichiamo con \(\sigma(t)\) il modulo della velocità
\[ \sigma (t) = |v(t)| \]In genere il modulo della velocità non è costante, ma varia a seconda del parametro. Un parametro fondamentale è l’ascissa curvilinea, indicata con \(s(t)\), che indica la distanza percorsa da un istante iniziale fino al tempo \(t\). L’ascissa curvilinea è così definita:
\[ s = g(t) = \int_{t_{0}}^{t}|\frac{dp}{dt}|dt \]dove \(|\frac{dp}{dt}|= \sqrt{x'(t)^{2}+ y'(t)^{2}}\). Se si utilizza il parametro \(s\) si vede che il modulo della velocità è costante, uguale a \(1\).
Esempio 7.1 – La circonferenza
La circonferenza di un cerchio di centro \((0,0)\) e raggio uguale a \(1\), ha le seguenti equazioni parametriche espresse con l’ascissa curvilinea:
Possiamo utilizzare una diversa parametrizzazione, ad esempio la seguente, nella quale la velocità non è costante:
\[ \begin{split} p(t) &=(\cos (t^{2}), \sin (t^{2})) \quad t \in [0,\sqrt{2\pi}] \\ v(s) &=(-2t\sin (t^{2}), 2t\cos (t^{2})) \\ \sigma (t) & = 2t \end{split} \]In diverse situazioni è necessario che la velocità di un oggetto lungo la curva risulti costante (ad esempio se si tratta dl moto di una telecamera). Se si ha una curva di equazione \(q(t)\) e si vuole che la velocità sia costante, si deve trovare la relazione del parametro \(t\) con l’ascissa curvilinea \(t=f(s)\). Questo processo si chiama riparametrizzazione. Supponendo che \(p(s)\) sia una parametrizzazione naturale con l’ascissa curvilinea, si deve porre \(p(s)=q(t)\) e risolvere rispetto a \(t\). Nel caso dell’esempio sopra del cerchio la soluzione è facile: \( t= \sqrt{s}\). Nel caso generale si deve calcolare il seguente integrale, per ogni valore di \(t\):
\[ s=g(t) = \int_{t_{0}}^{t}|\frac{dq}{dt}|dt \]Questa equazione integrale, fissato un valore di \(t\), permette di calcolare la lunghezza \(s(t)\). Il calcolo di questo integrale in genere richiede l’utilizzo di metodi di analisi numerica, tra i quali uno dei più semplici è il metodo di Cavalieri-Simpson (Wikipedia).
In realtà serve la funzione inversa: dato un valore di \(s\) determinare il tempo \(t\) in cui la lunghezza assume proprio quel valore: \(t = g^{-1}(s)\). Tranne nei casi più semplici, in genere non esiste una soluzione in forma chiusa, ma si deve ricorrere ai metodi dell’analisi numerica. L’algoritmo più famoso è il metodo di Newton per trovare gli zeri di una funzione (Wikipedia). La funzione è in questione è \(F(t)=g(t)-s\) dove \(s\) è una valore fissato costante. Il metodo di Newton per trovare gli zeri di \(F(t)\) è basato sulla seguente iterazione:
dove \(F'(t)=|\frac{dq}{dt}|\).
Quindi, ricapitolando, data una curva di Bézier \(p(t)\), se vogliamo che l’oggetto (Game Object) si muova lungo la curva a velocità costante, dobbiamo fare i seguenti passi:
- determinare la lunghezza totale della curva, utilizzando il metodo di Simpson o un altro metodo per il calcolo approssimato dell’integrale
- dividere la curva in tratti di uguale lunghezza, e per ogni valore del parametro \(s\) determinare il corrispondente valore del parametro \(t\), utilizzando il metodo di Newton
- calcolare il valore \(p(t)\) con la formula di Bézier
Per il metodo di Simpson e l’algoritmo di Newton vedere un testo di analisi numerica, ad esempio il libro di Quarteroni.
Conclusione
Le spline hanno una grande importanza nello sviluppo dei videogiochi. Gli sviluppatori devono avere una conoscenza delle proprietà dei vari tipi di curve e scegliere quella che si adatta meglio al problema. Per completezza in un prossimo articolo descriveremo altri due tipi di curve: le B-Spline e le NURBS.
Bibliografia
[1]Seymour Lipschutz – Schaum’s Outline of Linear Algebra (MacGraw-Hill)
[2]A. Quarteroni, R. Sacco – Matematica Numerica (Springer Verlag)
[3]F. Scheid – Numerical Analysis (Schaum’s outline series)
[4]G. Lorentz – Bernstein Polynomials (Ams Chelsea Publishing)
[5]E. Catmull, R. Rom – A Class of Local Interpolating Splines, in Computer Aided Geometric Design (Academic Press, 1974)

0 commenti