In questo breve articolo presenteremo alcuni problemi relativi alla determinazione dei punti a coordinate intere contenuti all’interno o sulla frontiera di alcune figure piane. Questo tipo di problema presenta aspetti molto interessanti e trova importanti applicazioni in vari settori della matematica.
1) Il reticolo piano degli interi
Un punto del piano \((x,y) \in R^{2}\) viene chiamato punto intero (lattice point) se entrambe le coordinate cartesiane sono intere, cioè se \(x,y \in \mathbf{Z}\). Si chiama reticolo piano degli interi l’insieme dei punti interi del piano. Possiamo indicarlo con il simbolo \(\mathbf{Z}^{2}\).
Esercizio 1.1
Dimostrare che non può esistere un triangolo equilatero con tutti e tre i vertici interi.
Vale anche il seguente teorema, la cui dimostrazione non è semplice:
Teorema 1.1
L’unico poligono regolare che può essere disegnato nel piano, con tutti i vertici nei punti del reticolo, è il quadrato.
Per una dimostrazione vedere [1].
2) Il numero di punti interi contenuti all’interno di un cerchio
Il seguente problema è stato proposto da Steinhaus nel 1957[2]:
Problema 2.1 (Steinhaus)
Dato un numero naturale \(n\), verificare se esiste un cerchio del piano che al suo interno contiene esattamente \(n\) punti a coordinate intere.
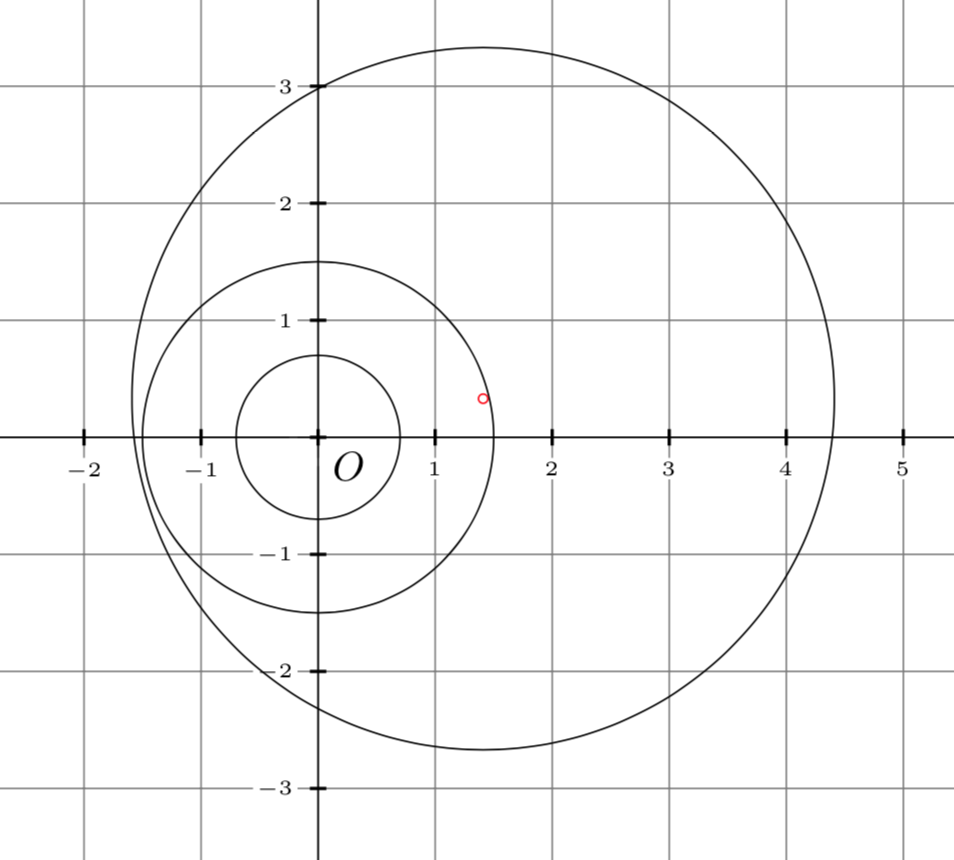
Conviene distinguere due casi:
Caso a) Cerchio con il centro su un punto del reticolo
In questo caso esistono dei numeri naturali \(n\) per i quali non è possibile trovare cerchi che contengono \(n\) punti interi. Ad esempio non esistono cerchi che contengono 2,3,4 punti interi.
Caso b) Cerchio con il centro in un punto che non appartiene al reticolo
In questo caso vale il seguente teorema:
Teorema 2.1 – Steinhaus
Per ogni numero naturale \(n\) esiste un cerchio che contiene esattamente \(n\) punti al suo interno.
Per dimostrare il teorema utilizzeremo il seguente lemma:
Lemma 2.1
Esiste un punto del piano tale che tutti i punti del reticolo degli interi hanno distanze diverse con il punto.
Dimostrazione
Definiamo il punto \(C(\sqrt{u}, \frac{1}{v})\), dove \(u,v\) sono interi positivi, \(u >1\) libero da quadrati, e \(v >2\). Se due punti distinti del reticolo degli interi \(P(a,b)\) e \(Q(c,d)\) hanno le stessa distanza dal punto \(C\), allora applicando la formula di Euclide abbiamo:
Tenendo conto che \(\sqrt{u}\) è un numero irrazionale, si trova facilmente che deve essere \(a=c\) e \(b=d\), contrariamente all’ipotesi che i punti \(P,Q\) sono distinti.
Chiaramente c’è un numero infinito di punti che si possono scegliere. Un esempio è il punto \(C(\sqrt{2},\frac{1}{3})\) proposto da Sierpinski.
Utilizzando il lemma precedente si dimostra facilmente il teorema 2.1. Basta mettere in ordine crescente di distanza i punti interi del reticolo, e fermarsi quando raggiungiamo il numero \(n\) di punti.
Nota
Steinhaus ha anche dimostrato che per ogni intero positivo \(n\) esiste un cerchio che ha area uguale a \(n\) e contiene esattamente \(n\) punti interi al suo interno.
3) Il teorema di Jacobi
Ricordiamo un importante teorema di Jacobi che è utile per il problema del paragrafo successivo. Definiamo la funzione aritmetica \(r_{2}(n)\) come il numero delle rappresentazioni di \(n\) nella forma
\[ n = x^{2} + y^{2} \quad \text { \(x,y \in \mathbf{Z}\)} \]Si conviene di contare come diverse anche le rappresentazioni che differiscono in maniera banale rispetto al segno o all’ordine. Ad esempio \(r_{2}(1)=4\), poiché:
\[ 1 = (\pm 1)^{2}+ 0^{2}= 0^{2}+(\pm 1)^{2} \]Definiamo inoltre le due funzioni aritmetiche \(d_{1}(n)\) e \(d_{3}(n)\) rispettivamente come il numero dei divisori di \(n\) della forma \(4k+1\) e della forma \(4k+3\).
Il seguente teorema è stato dimostrato dal grande matematico Jacobi(1804-1851) nella sua fondamentale opera ‘Fundamenta Nova Theoriae Functionum Ellipticarum’ pubblicata nel 1829.
Teorema 3.1 – Jacobi
\[ r_{2}(n)=4 (d_{1}(n) – d_{3}(n)) \]Per una dimostrazione vedere ad esempio il testo [3].
Una conseguenza immediata del teorema di Jacobi è il seguente teorema:
Teorema 3.2
Il numero di soluzioni intere dell’equazione diofantea:
è uguale a \(4(t+1)\).
Osserviamo anche che ogni soluzione \((A,B)\) con \( A \neq 0, B \neq 0\), da luogo ad un gruppo di \(8\) soluzioni \((\pm A, \pm B),(\pm B, \pm A)\).
Esercizio 3.1
Supponiamo \(t=2m, m \ge 1\). Dimostrare che le soluzioni intere dell’equazione del teorema 3.2 devono essere del tipo seguente:
Suggerimento
Osservare che \(5^{t}=25^{m} \equiv 1 \pmod{8}\).
4) Numero di punti interi contenuti sulla circonferenza
Problema 4.1
Dato un numero naturale \(n\), verificare se esiste un cerchio del piano che contiene nella sua circonferenza esattamente \(n\) punti a coordinate intere.
La risposta al problema è affermativa. Vale infatti il seguente teorema dimostrato da Schinzel[4]:
Teorema 4.1 – Schinzel
Per ogni \(n \ge 0\) esiste un cerchio la cui circonferenza attraversa esattamente \(n\) punti interi.
Dimostrazione
Supponiamo prima \(n\) pari; poniamo \(n=2(t+1)\). Consideriamo il seguente cerchio:
Il numero delle soluzioni intere di questa equazione è la metà del numero totale fornito dal teorema 3.2 (è il caso del primo termine dell’equazione dispari e secondo pari), e quindi è \(2(t+1)=n\).
Supponiamo ora che \(n\) sia dispari, con \(n=2m+1\) e \(t=2m\). L’equazione del cerchio da considerare è la seguente:
Il numero di soluzioni intere di questa equazione è uguale al numero di soluzioni \((X,Y)\) dell’equazione del teorema 3.2, che soddisfano il vincolo \(X \equiv -1 \pmod{4}\). In base all’esercizio 3.1 queste soluzioni sono un quarto del totale, nel caso \((X \neq 0; Y \neq 0)\). A queste va aggiunta la soluzione \((-5^{m},0)\). Mettendo insieme abbiamo che il numero totale delle soluzioni intere del cerchio è:
\[ 1 + \frac{4(t+1)-4}{4}=t+1=n \]Schnitzel nel suo articolo ha presentato le seguenti equazioni di due cerchi che soddisfano il teorema, rispettivamente nel caso pari e nel caso dispari:
\[ \begin{split} \left(x – \frac{1}{2}\right)^{2}+ y^{2}&=\frac{1}{4}5^{t-1} \quad \text{ n=2t} \\ \left(x – \frac{1}{3} \right)^{2}+ y^{2}&=\frac{1}{9}5^{2t} \quad \text{ n=2t+1} \\ \end{split} \]5) Il caso del quadrato
Per il quadrato esiste un teorema analogo a quello di Steinhaus:
Teorema 5.1
Per ogni numero naturale \(n\) esiste un quadrato che contiene al suo interno esattamente \(n\) punti del reticolo degli interi.
Per una dimostrazione vedere ad esempio [5].
Più facile è il caso dei punti interi sulla frontiera, che proponiamo come esercizio:
Esercizio 5.1
Dimostrare che per ogni numero naturale \(n\) esiste un quadrato nel piano che ha esattamente \(n\) punti interi sulla sua frontiera.
Conclusione
In questo articolo ci siamo limitati al reticolo piano. È naturale estendere lo studio nello spazio a tre dimensioni, e determinare il numero dei punti interi contenuti all’interno o sulla superficie di figure geometriche tridimensionali: sfera, cubo, piramide, ecc.
In un prossimo articolo studieremo i due classici problemi del cerchio di Gauss e dell’iperbole di Dirichlet, che hanno un ruolo importante nella teoria dei numeri.
Bibliografia
[1]D. Klobučar – On nonexistence of an integer regular polygon (Mathematical Communications, 3(1), 143-146, 1998)
[2]H. Steinhaus – One Hundred Problems in Elementary Mathematics (Dover Publications Inc., New York, 1964)
[3]Hardy-Wright – An introduction to the Theory of Numbers (V edition – Oxford, 1979)
[4]Schinzel – Sur l’existence d’un cercle passant par un nombre donne de points aux coordonneesentieres (L’Enseiqnement Math. (2) 4, 1958)
[5]Sierpinski – Sur quelques problemes concernant les points aux coordonnees entieres (L’Einseignement Math. (2) 4, 1958, 25-31)
0 commenti