Dopo aver descritto i principi generali della fisica del moto piano in un precedente articolo (vedi link), studiamo ora le leggi del moto circolare di un punto materiale e del moto rotatorio piano di un corpo rigido. Per la simulazione dei moti faremo riferimento alle funzionalità messe a disposizione dal motore Unity Physics 2D.
1) Moto circolare di un punto materiale
Un punto materiale di massa \(m\) compie un moto circolare se la traiettoria è una circonferenza. Naturalmente il punto può rappresentare anche un oggetto grande, come un pianeta; in tal caso in genere si considera il punto materiale con posizione coincidente con il baricentro del pianeta e massa uguale alla massa totale del pianeta stesso. Il moto circolare si dice uniforme se la velocità è costante.
La posizione di un punto materiale in moto circolare può essere specificata mediante un solo parametro, ad esempio la distanza percorsa misurata sulla circonferenza, a partire da un punto fisso iniziale. Tale parametro viene chiamato ascissa curvilinea e viene indicato con il simbolo \(s(t)\), dove \(t\) è il tempo. Si deve definire il segno della distanza percorsa, ad esempio positivo se il moto avviene in senso antiorario, negativo se in senso orario.
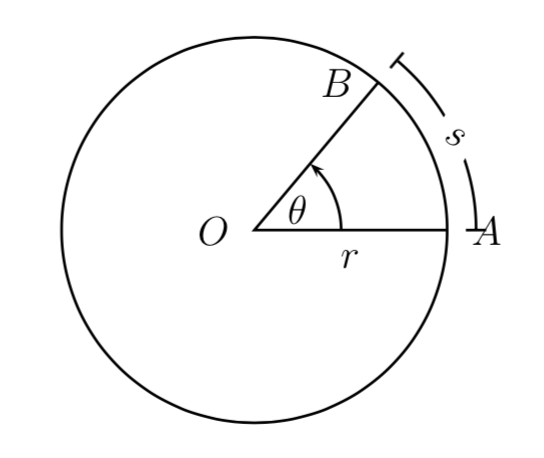
L’angolo di rotazione viene in genere misurato in radianti (ricordiamo che \(2 \pi\) radianti corrispondono ad un angolo giro di \(360\) gradi), e può essere calcolato con la seguente formula:
\[ \theta = \frac{s}{r} \]Le coordinate cartesiane del punto materiale che si muove di moto circolare sono le seguenti:
\[ \begin{split} x(t) = r \cos \theta (t) \\ y(t) = r \sin \theta (t) \end{split} \]In forma vettoriale, il vettore posizione è il seguente:
\[ \mathbf{r}(t)= x(t) \mathbf{i}+ y(t) \mathbf{j} \]La velocità del punto materiale è tangenziale alla traiettoria:
\[ v(t) = \frac{ds}{dt} = r \frac{d \theta}{dt}= r \omega (t) \]dove la grandezza \(\omega= \frac{d \theta}{dt}\) viene chiamata velocità angolare. Nel caso di moto circolare uniforme la grandezza \(\omega\) è costante e la relazione diventa \(\theta (t) = \theta_{0} + \omega t\), dove \(\theta_{0}\) è l’angolo all’istante iniziale \(t=0\).
La velocità angolare può essere considerata una grandezza vettoriale, con direzione perpendicolare al piano del moto e verso attribuito secondo la regola della mano destra. In termini vettoriali possiamo scrivere la seguente equazione:
In realtà la velocità angolare non è esattamente un vettore, ma uno pseudovettore o vettore assiale, in quanto il verso non cambia se invertiamo il verso degli assi coordinati.
L’accelerazione angolare è ottenuta derivando la velocità angolare:
Ricordiamo che in generale l’accelerazione di un punto materiale che si muove secondo una traiettoria nel piano ha due componenti, una tangenziale alla traiettoria e una perpendicolare:
\[ \begin{split} \mathbf{a} &= \frac{d\mathbf{v}}{dt}=\mathbf{a_{\tau}}+ \mathbf{a_{r}} \\ a_{\tau} &= \frac{dv}{dt} \\ a_{r} &= \frac{v^{2}}{r} \\ \end{split} \]dove \(a_{\tau}\) è l’accelerazione tangenziale e \(a_{r}\) è l’accelerazione radiale o normale.
Nel caso del moto circolare il raggio è costante e quindi otteniamo la seguente relazione fra l’accelerazione lineare e quella angolare:
\[ a_{\tau}(t) = r \alpha (t) \]Se il moto è circolare uniforme allora l’accelerazione angolare è nulla. In questo caso esiste solo l’accelerazione centripeta diretta verso l’origine.
Esercizio 1.1
Sia data la seguente equazione della traiettoria di un punto materiale:
dove \(\omega\) è una costante.
Dimostrare che il vettore posizione \(\mathbf{r}\) e il vettore velocità \(\mathbf{v}(t)\) sono perpendicolari fra loro. Dimostrare che l’accelerazione angolare è nulla mentre l’accelerazione centripeta ha modulo uguale a \(\omega^{2}r\).
2) Moto rotatorio di un corpo rigido
Mentre il movimento circolare è il movimento riguardante un punto materiale, il movimento rotatorio si riferisce ad un corpo esteso. Il moto dei corpi estesi in generale presenta grandi difficoltà, tuttavia c’è una classe importante di corpi per i quali lo studio del moto è semplificato: i corpi rigidi.
Un oggetto fisico di massa \(m\) si dice corpo rigido se la distanza fra ogni coppia di punti rimane invariata nel tempo. Si tratta di un modello ideale, perché nella realtà nessun corpo è effettivamente rigido, in quanto le forze esterne e le forze centrifughe dovute al movimento tendono a modificare le distanze. Tuttavia in molte situazioni l’effetto delle distorsioni è abbastanza piccolo da poter essere trascurato.
Il moto rotatorio di un corpo rigido intorno ad un asse fisso è caratterizzato dalle seguenti proprietà:
- ogni punto del corpo compie un moto circolare
- tutte le circonferenze sono concentriche e stanno su piani paralleli
- esiste un asse di rotazione perpendicolare ai piani delle circonferenze
- nel moto rotatorio l’asse di rotazione in genere passa attraverso il corpo stesso. Se l’asse è esterno al corpo si parla più propriamente di moto di rivoluzione
2.1) Il momento di inerzia
Nell’equazione di Newton \(\mathbf{F}=m \mathbf{a}\), la massa è la grandezza fisica che oppone resistenza al cambiamento di moto lineare. Nella rotazione esiste una grandezza simile che si oppone alla variazione dello stato di rotazione di un corpo rigido, il momento di inerzia. Mentre la massa dipende solo dalla quantità di materia contenuta nel corpo, il momento di inerzia dipende oltre che dalla massa anche dalla forma geometrica.
Il caso più semplice per la definizione del momento di inerzia è quello di un corpo di massa \(m\) assimilabile ad un punto materiale. In tal caso il momento di inerzia rispetto ad un asse rispetto al quale il corpo ruota è:
dove \(r\) è la distanza del corpo dall’asse.
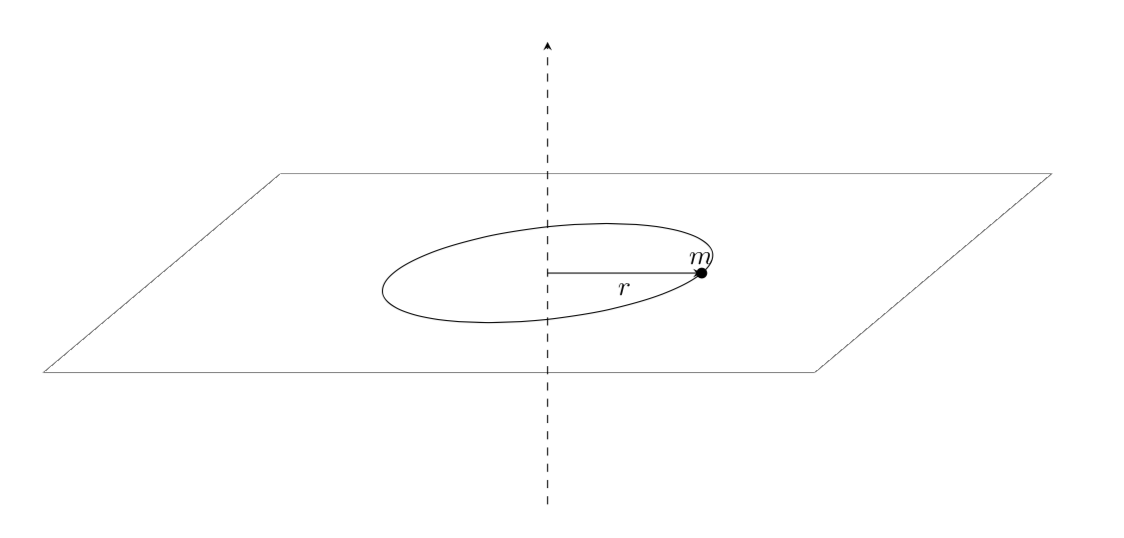
Nel caso di un sistema di \(n\) punti materiali di masse \(m_{i}\) e distanze dall’asse \(r_{i}\) il momento di inerzia è:
\[ I = \sum_{i=1}^{n}m_{i}r_{i}^{2} \]La definizione per un sistema di particelle si estende facilmente al caso di un corpo rigido continuo, nel qual caso per il calcolo si utilizzano gli integrali, che come è noto sono definiti come limiti di somme. Alcuni casi sono illustrati nella seguente tabella:

Per una panoramica più vasta sui momenti di inerzia vedere il seguente link a Wikipedia.
2.2) Il momento angolare
Per un corpo rigido che si muove nello spazio, il momento angolare \(\mathbf{L}\) è così definito:
\[ \mathbf{L}= \mathbf{r} \times \mathbf{p} \]dove \(\mathbf{r}\) è il vettore posizione e \(\mathbf{p}=m \mathbf{v}\) è la quantità di moto. In generale il vettore posizione e la velocità sono funzioni del tempo. In alcuni casi anche la massa può variare nel tempo, ad esempio nei razzi inviati nello spazio oppure nei problemi della teoria della relatività ristretta, nei quali sono in gioco velocità paragonabili a quelle della luce.
Il calcolo del momento angolare nel caso generale di moto nello spazio a tre dimensioni è complesso. In questo articolo ci limiteremo ai moti piani; il moto di un corpo rigido si dice piano quando tutti i punti del corpo stesso si muovono parallelamente ad un piano fisso. In questo caso l’asse di rotazione è fisso, cioè la direzione è sempre la stessa, anche se l’asse stesso può traslare.
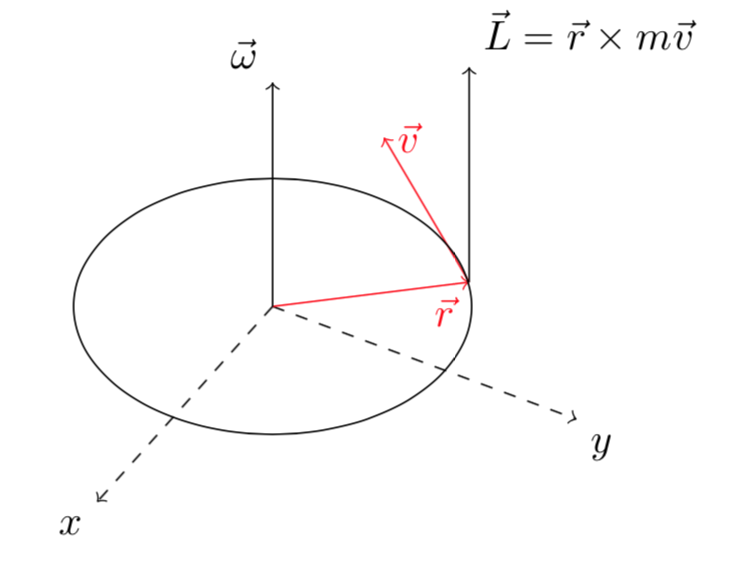
Nel caso di un corpo rigido con moto rotatorio intorno ad un asse di rotazione fisso, il modulo del momento angolare è dato da
\[ L=I \omega \]2.3) Legge di Newton del moto rotatorio
Per il moto rotatorio esiste una legge analoga a quella di Newton \(\mathbf{F}= m \mathbf{a}\). Al posto della forza c’è il momento esterno (torque) \(\mathbf{M}\) e al posto della quantità di moto c’è il momento angolare. Il momento esterno è il momento che una forza esercita su un corpo rispetto ad un punto o ad un asse di riferimento. La distanza dal punto di riferimento o dall’asse si chiama braccio della forza. La definizione del momento esterno è la seguente:
\[ \mathbf{M} = \mathbf{r} \times \mathbf{F} \]dove \(\mathbf{r}\) è il vettore che va dall’asse di rotazione al punto in cui agisce la forza. Il modulo del momento esterno è quindi:
\[ M = rF \sin \theta \]dove \(\theta\) è l’angolo fra il vettore \(\mathbf{r}\) e la forza applicata \(\mathbf{F}\).
L’equazione fondamentale del moto rotatorio è la seguente:
Si tratta di una equazione vettoriale, in quanto \(\mathbf{M}\) e \(\mathbf{L}\) sono vettori. Nel caso di moto rotatorio piano con asse di rotazione fisso abbiamo \(L=I \omega\); supponendo il momento inerzia costante l’equazione si riduce alla seguente:
\[ M = \frac{d (I\omega)}{dt}= I \frac{d\omega}{dt} \]Il significato dell’equazione precedente è simile a quello della classica equazione di Newton. Se non è applicato un momento esterno su un corpo rigido, non c’è accelerazione angolare e quindi la velocità angolare rimane costante o uguale a zero. Il momento di inerzia misura la resistenza alla variazione dello stato di rotazione, in modo simile alla massa che resiste alla variazione di velocità nel moto lineare.
La seguente tabella illustra la corrispondenza fra le grandezze fisiche utilizzate per il moto piano lineare e quelle relative al moto rotatorio.

2.4) Principio di conservazione del momento angolare
Se il momento totale delle forze esterne che agiscono su un sistema di corpi materiale è nullo, allora il momento angolare complessivo del sistema è costante.
Questo principio è analogo al principio di conservazione della quantità di moto. Nel caso semplice di un corpo in rotazione intorno ad un asse fisso, in assenza di momenti di forze esterne, si conserva il momento angolare \(L = I \omega\). Naturalmente le grandezze \(I\) e \(\omega\) possono variare, purché il prodotto si mantenga costante. Il caso classico è quello del tuffatore che rannicchiandosi su se stesso fa diminuire il momento di inerzia rispetto all’asse di rotazione e di conseguenza aumenta la velocità angolare.
Per un ripasso della fisica delle rotazioni vedere [1], oppure [2].
3) Le rotazioni in Unity 2D senza il motore fisico
Unity utilizza internamente i quaternioni per gestire le rotazioni (vedi link). Ogni quaternione è rappresentato da quattro numeri reali, che tuttavia non sono gli angoli di rotazione e sono quindi di difficile interpretazione. Per facilitare la comprensione delle grandezze in gioco nelle rotazioni, Unity effettua una trasformazione e visualizza nell’Inspector gli angoli di Eulero equivalenti.
Unity offre vari metodi per realizzare il moto circolare e rotatorio nel piano, senza utilizzare il motore fisico. Tra i principali metodi ricordiamo i seguenti:
3.1) Transform.rotation
Imposta la rotazione di un oggetto in modo immediato, in base agli angoli specificati nei parametri, indipendentemente dallo stato precedente. Transform.rotation è un quaternione. Non è memorizzato in gradi x,y,z, anche se l’Inspector di Unity converte i quaternioni in gradi.
Quaternion target = Quaternion.Euler(0, 0, 90.0f);
transform.rotation = Quaternion.Slerp(transform.rotation, target, Time.deltaTime * 0.5f);3.2) Transform.localRotation
È simile al precedente metodo, con la differenza che imposta la rotazione di un oggetto in relazione all’oggetto padre, e non al world space.
3.3) Transform.eulerAngles
È simile al Transform.rotation, ma permette di impostare gli angoli mediante i gradi, che sono di più facile intuizione.
3.4) Transform.Rotate
Applica una rotazione all’oggetto intorno agli assi \(x,y,z\) in funzione dei gradi specificati nei parametri.
3.5) Transform.RotateAround
Effettua una rotazione rispetto ad un punto fisso e ad un asse di una grandezza angolare uguale al terzo parametro specificato. Esempio:
transform.RotateAround(target.position,new Vector3 (0, 0, 1), 45);In genere si può specificare la rotazione nel world space oppure nello spazio locale nel caso di oggetti legati ad altri da uno stato di parentela.
Il seguente esempio illustra l’utilizzo di transform.position e transform.rotate per ottenere un moto di rivoluzione e rotazione per la terra e la luna.

Il movimento della terra è simulato dalle seguenti istruzioni. In modo simile viene gestito il movimento della luna.
void Start(){
// v = raggio vettore dal centro del sole alla terra
v = transform.position - center.position;
}
void Update() {
// moto circolare di rivoluzione intorno al sole
v = Quaternion.AngleAxis(degreesPerSecond * Time.deltaTime, Vector3.forward) * v;
transform.position = center.position + v;
// moto rotatorio intorno al centro della terra
transform.Rotate(Vector3.forward * Time.deltaTime * 100F, Space.Self);
}4) Rotazioni con il motore Unity Physics 2D
Le funzioni messe a disposizione dal componente Rigidbody 2D utilizzano il motore fisico Physics 2D. Si possono applicare delle forze ad un oggetto e il motore fisico calcola la posizione in ogni FixedUpdate.
4.1) Rotazioni mediante l’utilizzo diretto delle forze
In un precedente articolo di questo blog abbiamo studiato l’utilizzo del metodo AddForce per gestire un moto di traslazione generico di un oggetto. Nel caso specifico del moto rotatorio Unity mette a disposizione un ulteriore metodo AddTorque. Come la AddForce, anche la funzione AddTorque applica una spinta rotatoria che agisce in funzione delle caratteristiche del corpo (massa, forma geometrica, ecc.). Come abbiamo visto in precedenza il torque è il momento che una forza esterna esercita su un corpo rispetto ad un punto di riferimento, causando una rotazione dell’oggetto stesso. Ricordiamo la relazione fra il momento esterno (torque) e la variazione del momento angolare:
\[ M = \frac{d (I\omega)}{dt}= I \frac{d\omega}{dt} \]La funzione Rigidbody2D.AddTorque aggiunge un momento e quindi causa una variazione della velocità angolare Rigidbody2D.angularVelocity, secondo la seguente formula:
Rigidbody2D.angularVelocity += Torque x Time.fixedDeltaTime x (1/Rigidbody2D.inertia)La variazione della velocità angolare causa una contestuale variazione dello stato di rotazione dell’oggetto (Rigidbody2D.rotation) secondo questa formula:
Rigidbody2D.rotation += Time.fixedDeltaTime x Rigidbody2D.angularVelocityL’esempio seguente è ottenuto mediante l’utilizzo del comando AddTorque.

4.2) Rotazioni senza usare direttamente le forze
In alternativa si può controllare la velocità angolare, senza utilizzare le forze, mediante la funzione Rigidbody2D.angularVelocity. Questa funzione permette di impostare direttamente la velocità angolare ad un ben preciso valore di gradi al secondo.
5) Il moto in presenza di attrito
L’attrito è una forza che agisce in direzione opposta al movimento. Ad esempio un’automobile rallenta quando premiamo i freni grazie all’attrito che agisce fra i freni e le ruote. L’intensità della forza di attrito dipende dal tipo di materiali che vengono in contatto. In fisica viene misurata mediante il coefficiente di attrito. Ci sono due tipi di forze di attrito: l’attrito statico e l’attrito dinamico.
5.1) Attrito statico
L’attrito statico è le forza che si esercita fra due corpi che vengono a contatto. Mediante gli esperimenti di fisica si trova la seguente relazione approssimata per la formula dell’attrito statico:
\[ f_{s}\le \mu_{s}N \]dove \(f_{s}\) è l’intensità della forza di attrito statico, \(\mu_{s}\) è il coefficiente di attrito statico e \(N\) è l’intensità della forza normale, cioè perpendicolare alla superficie di contatto. La forza di attrito statico si oppone alla forza applicata e aumenta fino ad un valore massimo \(f_{s}(max)=\mu_{s}N\). Quando la forza applicata supera questo valore massimo, il corpo inizia a muoversi, e inizia l’attrito dinamico.
5.2) Attrito dinamico
La forza di attrito dinamico è la forza d attrito che agisce quando tra i due corpi c’è un movimento relativo. Sperimentalmente si trova la seguente relazione approssimata per la formula dell’attrito dinamico:
\[ f_{d} =\mu_{d}N \]dove \(f_{d}\) è l’intensità della forza di attrito dinamico, \(\mu_{d}\) è il coefficiente di attrito dinamico e \(N\) è l’intensità della forza normale.
Il coefficiente di attrito dinamico è minore di quello statico. Per una panoramica dei coefficienti di attrito dei vari materiali vedere questo link a Wikipedia.
Esempio 5.1 – Il piano inclinato
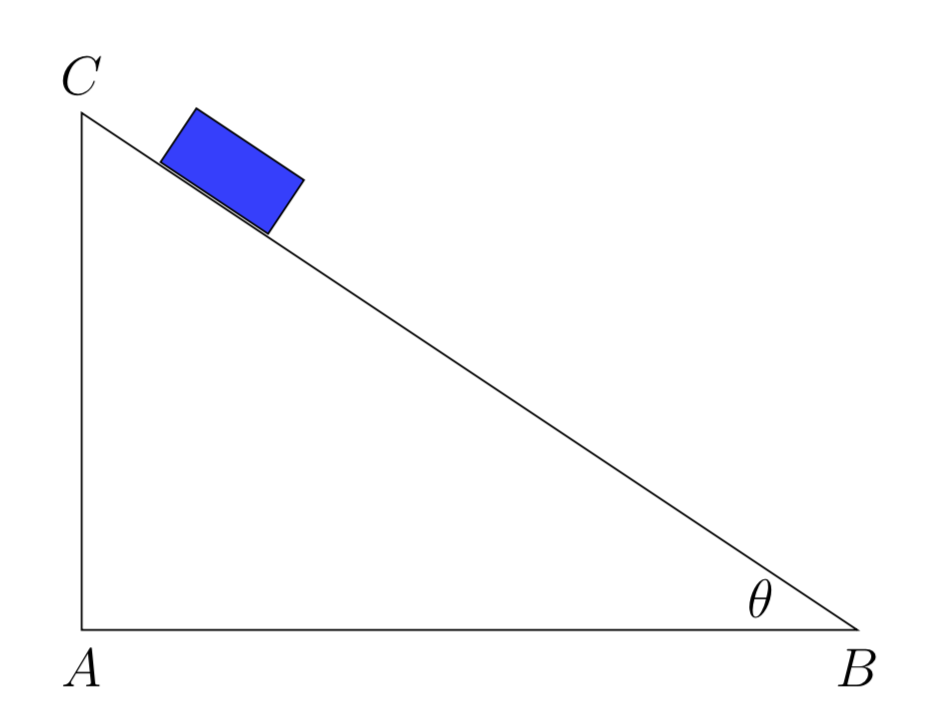
La differenza fra attrito statico e dinamico può essere illustrata mediante un blocco posto su un piano inclinato. Un piano inclinato di angolo \(\theta\) esercita una forza normale uguale a \(F_{n}=mg \cos \theta\). Il corpo è spinto lungo l’ipotenusa del triangolo con la forza \(F_{t}=mg \sin \theta\) dovuta alla gravità terrestre. Il corpo resta fermo fino a che la forza di attrito statico è maggiore di \(mg \sin \theta\). Quindi la condizione perché il corpo sia fermo è che \( \tan \theta \le \mu\). Ricordiamo che la tangente di \(\theta\) è data dal rapporto fra le lunghezze dei cateti AC e AB. Aumentando l’angolo oltre questa relazione il corpo inizia a muoversi ed entra in gioco l’attrito dinamico.
Esempio 5.2 – Moto di puro rotolamento
Un esempio di moto in cui l’attrito ha un ruolo essenziale è il moto di puro rotolamento, ad esempio il moto di rotolamento nel piano di un disco che ruota senza senza strisciare: di fatto questo implica che la velocità del punto di contatto del disco con il piano è nulla.
Possiamo scomporre il moto in due parti: il centro di massa si muove con velocità \(v_{cm}\) e il corpo ruota intorno al centro di massa con velocità angolare \(\omega\). Tra le due grandezze ci deve essere la seguente relazione
Il moto di puro rotolamento è possibile solo se c’è l’attrito statico. Se non ci fosse attrito statico il disco ruoterebbe, ma il suo centro di massa sarebbe sempre fermo. La traiettoria di un punto generico \(P\) del disco è una cicloide:
\[ \begin{split} x &= r(\omega t – \sin{\omega t}) \\ y &= r(1- \cos {\omega t}) \\ \end{split} \]
Per simulare il moto di traslazione del centro di massa e il moto di rotazione le istruzioni possono essere le seguenti:
m_Rigidbody.velocity = new Vector2(3.0f, 0);
m_Rigidbody.AddTorque(-1.50f, ForceMode2D.Impulse);5.3) Gestione della forza di attrito in Unity
In Unity 3D, che utilizza il motore fisico PhysX, sono previsti due parametri separati per definire il coefficienti di attrito statico e quello dinamico di un materiali fisico. Invece in Unity 2D è previsto un solo parametro. I due tipi di attrito sono simulati, tuttavia la gestione è interna a Unity 2D e al motore fisico Box 2D.
Conclusione
Unity 2D fornisce strumenti efficienti per simulare il moto nel piano. Il moto nello spazio è sicuramente più interessante, tuttavia in questo caso il problema è assai più complesso. Nei prossimi articoli descriveremo le leggi della fisica nello spazio tridimensionale e gli algoritmi numerici utilizzati per risolvere le equazioni.
Bibliografia
[1]Halliday, Resnick – Fundamentals of Physics (Wiley)
[2]H. Goldstein – Meccanica classica (Zanichelli)

0 commenti