Angoli di Eulero, Quaternioni di Hamilton e Videogiochi

Nella programmazione dei videogiochi, come in molti settori della scienza e della tecnologia, è fondamentale poter calcolare le coordinate di un oggetto in diversi sistemi di riferimento, legati tra loro da operazioni di traslazione, rotazione o cambiamenti di scala.
Il problema è particolarmente complesso per quanto riguarda le rotazioni. In un articolo precedente abbiamo analizzato la rappresentazione delle rotazioni mediante le matrici, mettendone i evidenza i pregi e anche i limiti. Gli angoli di Eulero vennero introdotti dal grande matematico Eulero ( 1707-1783) per studiare il moto di rotazione di un corpo rigido nello spazio euclideo a tre dimensioni. I quaternioni sono strutture algebriche, introdotte da Hamilton (1805-1865), che estendono il concetto di numero complesso. Nonostante siano meno intuitivi degli angoli di Eulero, si sono dimostrati uno strumento più efficiente per lo studio del moto di rotazione dei corpi. In questo articolo descriveremo le proprietà di questi due importanti argomenti e faremo riferimento al loro utilizzo nel framework UNITY 3D.

---

1) Gli angoli di Eulero

1.1) Teorema di Eulero

Ogni spostamento di un corpo rigido nello spazio tridimensionale, con un punto che rimane fisso, è equivalente ad una singola rotazione del corpo intorno ad un asse passante per il punto fisso.

Questo teorema è stato formulato da Eulero nel 1775. Quindi dato un corpo rigido con un punto fisso, che inizialmente sia in una configurazione \(C_{0}\) e dopo un intervallo di tempo \(t\) passi in una configurazione \(C_{t}\), il teorema afferma che si può sempre individuare una rotazione intorno ad un asse che colleghi queste due configurazioni.
In altri termini se abbiamo due sistemi di riferimento cartesiani \((x,y,z)\) e \((X,Y,Z)\) con la stessa origine ma diverso orientamento, esiste sempre un unico asse di rotazione con il quale il primo sistema assumerà la stessa configurazione del secondo. Ogni rotazione quindi può essere descritta mediante i tre angoli di Eulero, che specificano una sequenza di tre successive rotazioni, intorno agli assi coordinati. La tripletta degli angoli di Eulero viene usualmente indicata con la notazione (\(\phi\),\(\theta\),\(\psi\)).
Ci sono diverse convenzioni sul modo di esprimere gli angoli di Eulero, dipendenti dall’ordine delle rotazioni. Ciascuna delle tre rotazioni può essere effettuata intorno a un qualsiasi asse coordinato. Esistono quindi diverse sequenze possibili, di lunghezza \(3\), per definire in modo completo lo stato di rotazione di un oggetto.
Di seguito si fa riferimento alla convenzione associata agli angoli ZYZ caratterizzati dalle seguenti operazioni:

• Rotazione di un angolo \(\phi\) intorno all’asse z
• Rotazione di un angolo \(\theta\) intorno all’asse y (corrente)
• Rotazione di un angolo \(\psi\) intorno all’asse z (corrente)

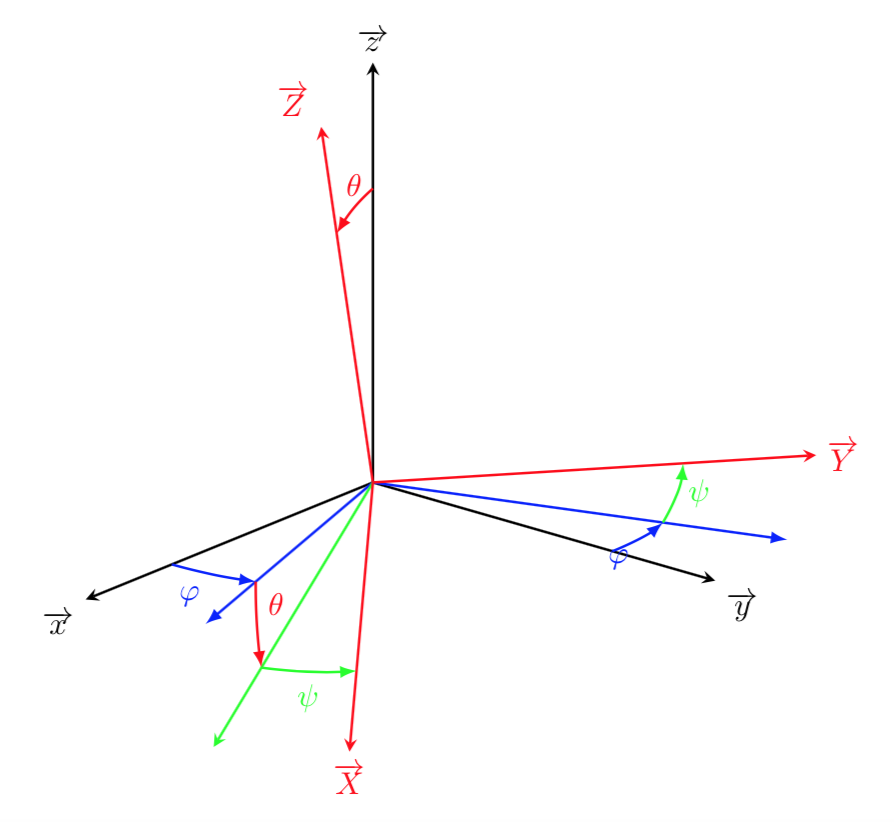
Ognuna delle tre rotazioni può essere rappresentata matematicamente mediante una matrice di rotazione. La matrice relativa alla rotazione complessiva viene calcolata moltiplicando le 3 matrici nell’ordine inverso.
Per un ripasso della rappresentazione delle rotazioni tramite matrici vedere l’articolo pubblicato su questo blog.

Per una rotazione intorno all’asse \(Z\) di un angolo \(\phi\):

\[ \left( \begin{array}{cccc} \cos \phi & -\sin \phi & 0 &0 \\ \sin \phi & \cos \phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]

Per una rotazione intorno all’asse \(Y\) di un angolo \(\theta\):

\[ \left( \begin{array}{cccc} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]

Per una rotazione intorno all’asse \(Z\) di un angolo \(\psi\):

\[ \left( \begin{array}{cccc} \cos \psi & -\sin \psi & 0 &0 \\ \sin \psi & \cos \psi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]

Quindi, moltiplicando nell’ordine inverso otteniamo la matrice relativa alla rotazione complessiva:

\( Rot(z,\psi)Rot(y,\theta)Rot(z,\phi)= \\ \left( \begin{array}{cccc} \cos \psi & -\sin \psi & 0 &0 \\ \sin \psi & \cos \psi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cccc} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cccc} \cos \phi & -\sin \phi & 0 &0 \\ \sin \phi & \cos \phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \\ \)

Data la matrice complessiva di rotazione \( Rot(z,\psi)Rot(y,\theta)Rot(z,\phi)\), è possibile determinare gli angoli di Eulero corrispondenti. Senza entrare nei dettagli matematici, ricordiamo tuttavia che il processo di conversione è abbastanza delicato, per la possibilità di avere due sequenze diverse per la stessa orientazione finale e anche per la presenza di casi degenerati, nel caso di valori particolari degli angoli.

1.2) Limiti della rappresentazione di Eulero

Gli angoli di Eulero hanno la caratteristica della semplicità, sono facili da comprendere e necessitano di solo 3 numeri reali floating point.
Una limitazione di cui soffrono è il cosiddetto Gimbal Lock. Applicando le rotazioni in sequenza può capitare che uno dei tre assi principali collassi in uno degli altri due. Ad esempio se ruotiamo di 90 gradi intorno all’asse X, l’asse Y collasserà sull’asse Z. In questa situazione si perde un grado di libertà in quanto le rotazioni intorno agli assi Y,Z diventano equivalenti.
Un altro inconveniente è che gli angoli dipendono dall’ordine delle tre rotazioni, rappresentata con l’indicazione degli assi di rotazione: ZYZ, XZX, YXY, ecc. Ogni combinazione da un risultato diverso, come è facile verificare.
Nonostante questi problemi, gli angoli di Eulero sono utilizzati comunemente in molti settori, tra i quali gli strumenti di modellizzazione CAD e i framework di sviluppo dei videogiochi. Ad esempio l’interfaccia di Unity 3D nel pannello Inspector visualizza gli angoli di Eulero per rappresentare lo stato di rotazione di un oggetto. Tuttavia all’interno dei programmi responsabili dei calcoli per simulare le rotazioni, Unity utilizza uno strumento matematico molto più potente, i quaternioni di Hamilton.

---

2) I quaternioni di Hamilton

I quaternioni vennero introdotti da Hamilton (1805-1865) come estensione a quattro dimensioni dei numeri complessi. Questi nuovi oggetti matematici hanno fornito uno strumento potente per gestire i complessi calcoli necessari per studiare le rotazioni nello spazio tridimensionale. Per una comprensione dell’algebra dei quaternioni è necessario conoscere i fondamenti del calcolo vettoriale nello spazio euclideo \(R^{3}\). Per questo si possono consultare i seguenti testi: ^[1], ^[2].   
I quaternioni possono essere considerati come estensioni dei numeri complessi. Come è noto un numero complesso \(z\) viene indicato con la notazione \(z= a + bi\), dove \(i\) è l’unita immaginaria definita da \(i^2=-1\). Per definire un quaternione \(\mathbf{q}\) si aggiungono altre due simboli \(j,k\):

\[ \mathbf{q} = w + xi + yj + zk \]

dove \(w\) è la parte reale, (\(i,j,k\)) denotano le tre unità immaginarie, e (\(x,y,z\)) denotano le tre componenti immaginarie.
È utile utilizzare una notazione abbreviata per rappresentare un quaternione \(\mathbf{q}=w+ \mathbf{v}\), dove \(w\) è la componente scalare e \(\mathbf{v}=(x,y,z)\) è il vettore con le componenti immaginarie \((x,y,z)\). Indicheremo con il simbolo \(\mathbb{H}\) la struttura algebrica dei quaternioni. L’algebra dei quaternioni è basata sulle seguenti regole introdotte da Hamilton:

\[ i^{2}=j^{2}=k^{2}=ijk=-1 \] \[ ij=k=-ji \] \[ jk=i=-kj \] \[ ki=j=-ik \]

2.1) Addizione e moltiplicazione di quaternioni

Dati due quaternioni

\[ \mathbf{q}_{1}= w_{1} + x_{1}i + y_{1}j + z_{1}k \quad e \quad \mathbf{q}_{2}= w_{2} + x_{2}i + y_{2}j + z_{2}k \]

la somma è definita così:

\[ \mathbf{q}_{1} + \mathbf{q}_{2}= (w_{1}+w_{2}) + (x_{1} + x_{2}) i + (y_{1}+y_{2})j + (z_{1}+z_{2})k \]

mentre il prodotto dei due quaternioni è definito così:

\[ \begin{split} \mathbf{q}_{1} \mathbf{q}_{2} = & \quad (w_{1}w_{2} – x_{1}x_{2} -y_{1}y_{2} – z_{1}z_{2}) \\ & + (w_{1}x_{2} + x_{1}w_{2} + y_{1}z_{2} – z_{1}y_{2})i \\ & + (w_{1}y_{2} – x_{1}z_{2} + y_{1}w_{2} + z_{1}x_{2})j \\ & + (w_{1}z_{2} + x_{1}y_{2} – y_{1}x_{2} + z_{1}w_{2})k \end{split} \]

Una notazione più sintetica del prodotto si ottiene se utilizziamo la notazione \(\mathbf{q}_{1}=w_{1} +\mathbf{v_{1}}, \quad \mathbf{q}_{2}=w_{2} +\mathbf{v_{2}} \quad \) :

\[ \mathbf{q}_{1} \mathbf{q}_{2}= w_{1}w_{2}-\mathbf{v_{1}} \bullet \mathbf{v_{2}} + w_{1}\mathbf{v_{2}} + w_{2}\mathbf{v_{1}} + \mathbf{v_{1}} \times \mathbf{v_{2}} \]

dove \(\mathbf{v_{1}} \bullet \mathbf{v_{2}}\) è il prodotto scalare dei due vettori e \(\mathbf{v_{1}} \times \mathbf{v_{2}}\) è il prodotto vettoriale.

2.2) Coniugato, norma e inverso di un quaternione

Il coniugato di un quaternione \(\mathbf{q}\) è un quaternione indicato con \(\mathbf{q}^{*}\) così definito:

\[ \mathbf{q}^* = q_0 – q_1 i – q_2 j – q_3 k \]

Moltiplicando un quaternione con il suo coniugato abbiamo:

\[ \begin{align} \mathbf{q} \mathbf{q}^* &= (q_0 + \mathbf{v})(q_0 – \mathbf{v}) \\ &= q_0^2 + q_1^2 + q_2^2 + q_3^2 \end{align} \]

La lunghezza o norma di un quaternione \(\mathbf{q}\) è così definita:

\[ N(\mathbf{q})=|\mathbf{q}| = \sqrt{\mathbf{q} \mathbf { q}^*} = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2} \]

Ogni quaternione, ad eccezione dello zero, ha un inverso rispetto al prodotto:

\[ \mathbf{q}^{-1} = \frac{\mathbf{q}^*}{|\mathbf{q}|^2} \]

Per effettuare la divisione fra due quaternioni basta moltiplicare il primo per l’inverso del secondo.

In base alle proprietà sopra illustrate, possiamo concludere che, mentre i numeri complessi costituiscono un campo algebrico, i quaternioni sono un corpo algebrico, in quanto per essi non vale la proprietà commutativa del prodotto. Inoltre i quaternioni hanno la struttura di spazio vettoriale di dimensione 4, sul campo dei numeri reali.
Lo svantaggio dei quaternioni è che non sono intuitivi per gli esseri umani, come gli angoli di Eulero. Tuttavia le loro caratteristiche li rendono indispensabili per i calcoli effettuati tramite i programmi software.

Esercizio 2.1: dato un quaternione \(\mathbf{q}=q_{0} +i q_{1} +jq_{2} +kq_{3} \), dimostrare che vale la seguente formula:

\[ q^{2}- 2q_{0}q +N(q)=0 \]

Esercizio 2.2: dati due quaternioni \(a,b \in \mathbb{H}\), dimostrare la seguente formula:

\[ N(ab) = N(a) N(b) \]

Esercizio 2.3: calcolare il quoziente dei due quaternioni

\(\mathbf{q}_{1}= 2 + i + 3j -k\) e \(\mathbf{q}_{2}=-1 +2i +j -4k\)

Risposta: \(\left(\frac {7+ 6i -7j +14k}{22}\right)\)

---

3) I quaternioni e le rotazioni

Come è noto una rotazione nello spazio tridimensionale  è una funzione \(\psi \colon  \mathbb{R}^{3} \to \mathbb{R}^{3}\) che preserva le lunghezze, gli angoli e l’orientamento. In simboli devono essere rispettate le seguenti relazioni:

\[ \left\| \psi (\mathbf{P}) \right\| = \left\|\mathbf{P} \right\| \] \[ \psi (\mathbf{P}_{1}) \bullet \psi (\mathbf{P}_{2}) = \mathbf{P}_{1} \bullet \mathbf{P}_{2} \] \[ \psi (\mathbf{P}_{1}) \times \psi (\mathbf{P}_{2}) = \psi (\mathbf{P}_{1} \times \mathbf{P}_{2}) \]

dove il simbolo \(\bullet\) indica il prodotto scalare di due vettori, e il simbolo \(\times\) indica il prodotto vettoriale. Definiamo con il simbolo \(Im (\mathbb{H})\) l’insieme dei quaternioni con la componente scalare uguale a zero. I quaternioni che appartengono allo spazio \(Im(\mathbb{H})\) si dicono quaternioni immaginari o puri. Possiamo quindi identificare \(Im( \mathbb{H})\) con lo spazio tridimensionale \(\mathbb{R}^{3}\). Ne segue quindi che dati due quaternioni immaginari \(\mathbf{P}_{1},\mathbf{P}_{2}\), il loro prodotto è dato dalla formula:

\[ \mathbf{P}_{1} \mathbf{P}_{2} = – \mathbf{P}_{1} \bullet \mathbf{P}_{2} + \mathbf{P}_{1} \times \mathbf{P}_{2} \]

Teorema 3.1
Sia \(\psi\) una rotazione nello spazio \(\mathbb{R}^{3}\). Definiamo una nuova funzione \(\Psi\), estensione della \(\psi\), sullo spazio \(\mathbb{H}\) con questa condizione:

\[ \Psi(s+ \mathbf{v})= s + \psi (\mathbf{v}) \]

Allora vale la seguente relazione:

\[ \Psi (\mathbf{P}_{1}\mathbf{P}_{2})=\Psi(\mathbf{P}_{1}) \Psi(\mathbf{P}_{2}) \]

dove \(\mathbf{P}_{1},\mathbf{P}_{2}\) sono quaternioni con parte scalare nulla (immaginari). Si dice che la funzione \(\Psi\) è un omomorfismo sullo spazio \(\mathbb{H}\).

Dimostrazione
Basta applicare la formula del prodotto di due quaternioni immaginari e le proprietà dell’operatore \(\psi\) applicate ai vettori dello spazio \(\mathbf{R}^{3}\).

In base al teorema precedente quindi le funzioni come la \(\Psi\) rappresentano rotazioni nello spazio tridimensionale.
Definiamo ora una classe di funzioni \(\Psi _{\mathbf{q}} (\mathbf{P}) = \mathbf{q} \mathbf{P} \mathbf {q}^{-1}\). Si dimostra facilmente che questa trasformazione rispetta l’invarianza della norma ed è un omomorfismo nello spazio \(\mathbb{H}\). Basta infatti applicare la definizione della funzione e ricordare che

\[ \mathbf{q} \mathbf {q}^{-1}=1 = \frac {\mathbf{q} \mathbf {q}^{*}}{\mathbf {q}^{2}} \]

Quindi ogni quaternione può essere associato alla rotazione di un angolo \(\theta\) intorno ad un asse \(\mathbf{v}\). Per trovare la formula di corrispondenza conviene studiare le proprietà dei quaternioni unitari.

---

4) I quaternioni unitari

Se \( \left\|\mathbf{q} \right\| =1 \) allora \(\mathbf{q}\) si chiama quaternione unitario.

Teorema 4.1
Un quaternione \(\displaystyle \mathbf{q}\) unitario può essere rappresentato nella forma

\[ \mathbf{q} =( \cos \theta, \mathbf{v} \sin \theta) \]

Dimostrazione
Se \(\left\|\mathbf{q} \right\|=1\) e \( \mathbf{q} =(w,(x,y,z))\), allora \(w^{2} + x^{2}+ y^{2}+ z^{2}=1\). Essendo \( w^{2} <1\) , possiamo assumere che  \(w= \cos \theta\), per qualche angolo \(\theta\).
Dalla identità trigonometrica \(\sin ^{2} \theta + \cos ^{2} \theta = 1\) deriva \(x^{2} + y^{2} + z^{2}= \sin ^{2} \theta\). Quindi \(\mathbf{v}\) è un vettore unitario \( (\frac{x}{r}, \frac{y}{r}, \frac{z}{r})\) con \(r=\sqrt {x^{2}+ y^{2}+z^{2}}\).

Il coniugato di un quaternione unitario \(\mathbf{q}=(\cos \theta, \mathbf{v} \sin \theta)\) può essere scritto quindi

\[ \mathbf{q}^{*}= (\cos \theta, -\mathbf{v} \sin \theta)=(\cos (-\theta), \mathbf{v} \sin (-\theta)) \]

Il prodotto di due quaternioni unitari è un quaternione unitario:

\[ \left\| \mathbf{q}_{1} \mathbf{q}_{2} \right\| = \left\|\mathbf{q}_{1} \right\| \left\|\mathbf {q}_{2}\right\|=1 \]

Teorema 4.2
L’inverso di un quaternione unitario è il coniugato, anch’esso unitario.

Dimostrazione
Il teorema segue direttamente dalle proprietà del coniugato. Comunque è utile avere conferma anche effettuando il prodotto con le rappresentazioni trigonometriche:

\[ \begin{split} \\ \mathbf{q} \mathbf{q}^{*} & = (\cos \theta, \mathbf{v} \sin \theta) (\cos (-\theta), \mathbf{v} \sin (-\theta)) \\ & = (\cos ^{2} \theta – \mathbf{v} \sin \theta \bullet \mathbf{v} \sin(-\theta),\mathbf{v} \cos \theta \sin \theta \\ & \quad + \mathbf{v} \cos \theta \sin (-\theta) + \mathbf{v} \sin (\theta) \times \mathbf{v} \sin (- \theta)) \\ & = (1,0) \end{split} \]

---

5) I quaternioni unitari rappresentano le rotazioni

Per rappresentare una rotazione nello spazio abbiamo bisogno di un vettore unitario \(\mathbf{u}\) nella direzione dell’asse di rotazione, e un angolo \(\theta\), che ci dice il valore della rotazione. Indichiamo quindi con \(R(\theta, \mathbf{v})\) l’operatore che applicato ad un vettore \(\mathbf{v}\) da come risultato la nuova posizione del vettore stesso dopo la rotazione.
Per calcolare il valore di \(R(\theta, \mathbf{v})\) in primo luogo si decompone il vettore nelle sue componenti, parallela e ortogonale all’asse di rotazione:

\[ \begin{split} & \mathbf{v}_{p} = (\mathbf{u} \bullet \mathbf{v}) \mathbf{u} \\ & \mathbf {v}_{o} = \mathbf{v} -( \mathbf{u} \bullet \mathbf{v}) \mathbf{u} \end{split} \]

Si può dimostrare che vale la seguente formula per il vettore risultante dopo la rotazione di un vettore \(\mathbf{v}\), di un angolo \(\theta\) intorno ad un asse \(\mathbf{u}\):

\[ \begin{split} R(\mathbf{v},\theta) &= R (\mathbf{v}_{p},\theta) + R(\mathbf{v}_{o},\theta) \\ & = (\cos \theta) \mathbf{v} + (1 – \cos \theta) \mathbf{u} (\mathbf{u} \bullet \mathbf{v}) + (\sin \theta)(\mathbf{u} \times \mathbf{v}) \end{split} \]

Per una dimostrazione, oltre ai testi citati in bibliografia, si può vedere il seguente link.

D’altra parte dato un quaternione puro \(\mathbf{P}=(0,\mathbf{v})\) e un quaternione unitario \( \mathbf{q}= (\cos \theta, \mathbf{u} \sin \theta)\) vale la seguente formula:

\[ \begin{split} \mathbf{q} \mathbf{P} \mathbf{q}^{*} & = (\cos \phi, \mathbf{u} \sin \phi)(0,\mathbf{v})(\cos \phi, -\mathbf{u} \sin \phi) \\ & = (0,(\cos ^{2} \phi-\sin^{2} \phi)\mathbf{v} + 2 \sin^{2} \phi(\mathbf{u} \bullet \mathbf{v}) \mathbf{u} \\ & \quad + 2 \sin \phi \cos \phi (\mathbf{u} \times \mathbf{v})) \\ & = (0,(cos 2\phi)\mathbf{v}+ (1- \cos 2\phi)(\mathbf{u} \bullet \mathbf{v}) \mathbf{u} + (\sin 2\phi)(\mathbf{u} \times \mathbf{v})) \end{split} \]

Confrontando le ultime due equazioni, possiamo concludere che sono equivalenti, con la sostituzione \(\theta = 2 \phi\).

Un altro modo di arrivare allo stesso risultato è il seguente. Sia \(\mathbf{q}= w+ \mathbf{u}\) un quaternione unitario. L’inverso di \(\mathbf{q}\) è \( \mathbf{q}^{-1}=\mathbf{q}^{*}= w-\mathbf{u}\). Dato un quaternione immaginario \(\mathbf{P}=(0,\mathbf{v})\) abbiamo:

\[ \begin{split} \mathbf{q}\mathbf{P}\mathbf{q}^{-1} & = (w+\mathbf{u})\mathbf{P}(w-\mathbf{u}) \\ & = (-\mathbf{u} \bullet {P}+ w\mathbf{P}+ \mathbf{u}\times \mathbf{P} + \mathbf{u} \times \mathbf{P})(w-\mathbf{u}) \\ & = -w\mathbf{u} \bullet \mathbf{P} + w^{2}\mathbf{P} + w\mathbf{u}\times \mathbf{P} + (\mathbf{u} \bullet \mathbf{P})\mathbf{u} -w \mathbf{P} \mathbf{u}- (\mathbf{u} \times \mathbf{P})\mathbf{u} \\ & = w^{2}\mathbf{P} + 2w \mathbf{u} \times \mathbf{P} + (\mathbf{u} \bullet \mathbf{P})\mathbf{u} – \mathbf{u} \times \mathbf{P} \times \mathbf{u} \end{split} \]

Utilizzando ora le seguente nota proprietà del calcolo vettoriale:

\[ \mathbf{v} \times (\mathbf{u} \times \mathbf{v}) = \mathbf{v} \times \mathbf{u} \times \mathbf{v}= v^{2}\mathbf{u}-(\mathbf{v} \bullet \mathbf{u})\mathbf{v} \]

possiamo scrivere:

\[ \mathbf{q} \mathbf{P} \mathbf{q}^{-1}= (w^{2} – \mathbf{u}^{2})\mathbf{P}+ 2w \mathbf{u} \times \mathbf{P}+ 2(\mathbf{u} \bullet \mathbf{P})\mathbf{u} \]

Posto \(\mathbf{u}= t \mathbf{A}\), dove \(\mathbf{A}\) è un vettore unitario, abbiamo:

\[ \mathbf{q} \mathbf{P} \mathbf{q}^{-1}=(w^{2} – t^{2})\mathbf{P} + 2wt \mathbf{A} \times \mathbf{P}+ 2 t^{2}(\mathbf{A} \bullet \mathbf{P}) \mathbf{A} \]

Confrontando con la formula di rotazione nello spazio tridimensionale scritta in intorno ad un asse arbitrario, abbiamo le seguenti relazioni:

\[ \begin{split} w^{2} – t^{2} & = \cos \theta \\ 2 w t & = \sin \theta \\ 2t^{2} & = 1 – \cos \theta \end{split} \]

Con pochi passaggi possiamo dedurre le seguenti formule:

\[ w=\cos \left (\frac{\theta}{2}\right); \quad t=\sin\left(\frac{\theta}{2}\right) \]

Quindi il quaternione unitario che corrisponde ad una rotazione intorno all’asse \(\mathbf{A}\) è:

\[ \mathbf{q} = \cos \left (\frac{\theta}{2}\right) +\mathbf{A} \sin \left(\frac{\theta}{2}\right); \]

Il prodotto di due quaternioni \(\mathbf{q}_{1},\mathbf{q}_{2}\) rappresenta la rotazione risultante dalla composizione delle due singole rotazioni.

5.1) Matrice di rotazione corrispondente ad un quaternione

Per calcolare la matrice corrispondente ad un quaternione, basta espandere le formula:

\[ \mathbf{q} \mathbf{P} \mathbf{q}^{-1}=(w^{2} – t^{2})\mathbf{P} + 2wt \mathbf{A} \times \mathbf{P}+ 2 t^{2}(\mathbf{A} \bullet \mathbf{P}) \mathbf{A} \]

Il risultato è la seguente matrice \(M\):

\[ \left( \begin{array}{ccc} 1-2y^{2}- 2z^{2} & 2xy -2wz & 2xz+2wy \\ 2xy+2wz & 1-2x^{2}-2z^{2} & 2yz-2wx \\ 2xz-2wy & 2yz+2wx & 1-2x^{2}-2y^{2} \\ \end{array} \right) \]

Data la matrice di rotazione sopra descritta, è possibile risalire al quaternione corrispondente con pochi passaggi. Si calcola la traccia della matrice \(M\)(somma degli elementi diagonali):

\[ Tr(M)= 3-4x^{2}-4y^{2}-4z^{2}=4w^{2}-1 \]

poiché il quaternione è unitario (\(x^{2}+ y^{2}+z^{2}+ w^{2}=1\)). Quindi:

\[ w=\sqrt {\frac{Tr(M)+1}{4}} \]

In modo simile si calcolano le altri componenti \(x,y,z\).

---

6) La gestione delle rotazioni in Unity

6.1) Il componente Transform

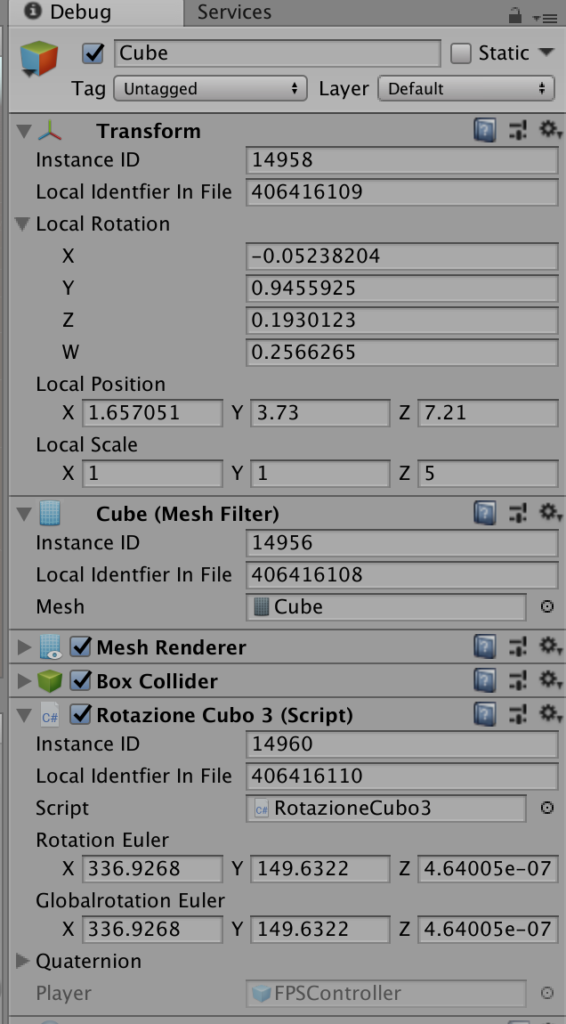
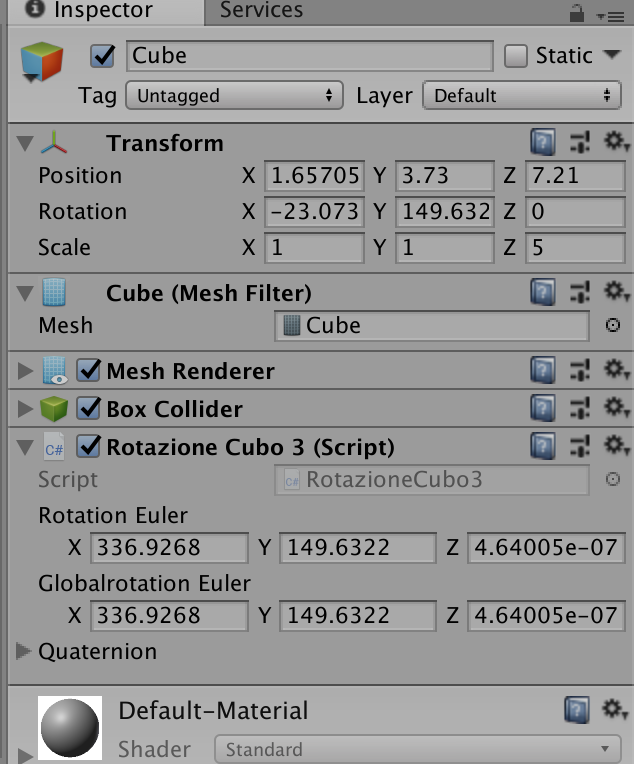
Ogni oggetto Unity, anche se non è visible sulla scena, ha il componente Transform, che contiene informazioni molto importanti sull’oggetto stesso a cui è associato. Tra queste ricordiamo la posizione, la rotazione e il fattore di scala. Praticamente il componente Transform è costituito da una matrice che memorizza le informazioni sulla posizione, rotazione e scala. Nell’editor di Unity i valori sono riferiti al sistema locale, mentre nella programmazione sono riferiti al sistema globale.

6.2) Le rotazioni

Unity utilizza i vettori e gli angoli di Eulero per rappresentare la posizione e la direzione di un oggetto, mentre internamente utilizza i quaternioni per gestire le rotazioni. Il componente Transform visualizza i valori degli angoli di Eulero se l’editor è in normal mode, mentre nel debug mode visualizza le componenti \((W,X,Y,Z)\) del quaternione.

Unity fornisce molte funzioni che collegano i vettori, gli angoli di Eulero e i quaternioni. Vediamo alcuni esempi:

// Creare un quaternione che rappresenta una rotazione di 40 gradi intorno a X, 15 intorno a Y e 10 intorno a Z
Quaternion quaternione = Quaternion.Euler(40, 15, 10);

// Creare un quaternione a partire dagli angoli di Eulero
Vector3 rotazioneEulero = new Vector3(40, 15, 10);
Quaternion quaternione = Quaternion.Euler(rotazioneEulero);

// Convertire quaternioni in angoli di Eulero 
Quaternion quaternione = transform.rotation;
Vector3 angoliEulero = quaternione.eulerAngles;
Debug.Log("Angoli di Eulero x: angoliEulero.x + " y: " angoliEulero.y + " z: " + angoliEulero.z);

La rotazione di un oggetto è simile allo spostamento, con la differenza che i vettori ora rappresentano gradi, invece di una posizione o direzione. Unity fornisce varie opzioni come Vector3.right, back, forward, down, up, left, right. Ad esempio per ruotare nella direzione negativa dell’asse orizzontale usare Vector.left, che è equivalente a (-1,0,0).

Tra le principali istruzioni messe a disposizione da Unity ricordiamo le seguenti, per le quali si rimanda alla documentazione UNITY 3D online:

• Quaternion.LookRotation
• Quaternion.Angle
• Quaternion.Euler
• Quaternion.Slerp
• Quaternion.FromToRotation
• Quaternion.identity

Esempio 6.1
Rotazione intorno all’asse X di un grado al secondo.

void Update () {
    transform.Rotate(Vector3.left * Time.deltaTime);
}

Esempio 6.2
Rotazione per inseguire un oggetto Target.

// Cerca un oggetto con identificativo "Target"
public Transform target = GameObject.Find("Target").GetComponent<Transform>();

// Calcolo del vettore differenza fra il Target e la nostra posizione
Vector3 vettoreDifferenza = target.position - transform.position;

// crea la rotazione
Quaternion rotazione = Quaternion.LookRotation(vettoreDifferenza);

// imposta la proprietà rotation del componente Transform
transform.rotation = rotazione;

---

Conclusione

Gli angoli di Eulero e i quaternioni di Hamilton sono due metodi molto importanti per la rappresentazione delle rotazioni degli oggetti nello spazio tridimensionale. Gli angoli di Eulero, nonostante siano più intuitivi, soffrono del problema del gimbal lock. I quaternioni non hanno una interpretazione fisica semplice. Tuttavia sono preferiti per effettuare i calcoli complessi, perché hanno una rappresentazione compatta, non hanno il problema del gimbal lock e hanno altri vantaggi, tra i quali ad esempio:

• semplicità per rappresentare la composizione di due rotazioni tramite il prodotto dei quaternioni
• l’interpolazione lineare sferica, con cui la quale è possibile generare orientazioni intermedie fra due stati di rotazioni, ottenendo un’animazione fluida

Le proprietà più avanzate dei quaternioni saranno oggetto di uno studio successivo. Per un approfondimento si può consultare il seguente testo: ^[3].

---

Bibliografia

^[1]Murray, Spiegel – Vector Analysis (McGraw-Hill)

^[2]H. Goldstein- Meccanica classica (Zanichelli)

^[3]Van Verth, Bishop – Essential Mathematics for Games and Interactive Applications (AK Peters)