1) Algebra delle matrici
Una matrice \(A\) formata da \(m\) righe e \(n\) colonne, definita sul campo dei numeri reali \(\mathbb{R}\) e indicata con \(A(m,n)\), è una collezione \((a_{ij})\) di numeri reali, indicizzati dai numeri naturali \(i\) e \(j\), con \(1\le i\le m\) e \(1\le j\le n\), rappresentata in questo modo:
\[ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \]Un vettore colonna è una matrice \(m\times 1\) per qualche \(m\), mentre un vettore riga è una matrice \(1\times n\) per qualche \(n\). Il simbolo \(\mathbb{R}^{m\times n}\) viene utilizzato per rappresentare l’insieme delle matrici \(m\times n\) con coefficienti reali. Le definizioni delle matrici e delle operazioni possono essere estese in modo simile nel campo dei numeri complessi \(\mathbb{C}\). Date due matrici dello stesso ordine, sono definite in modo semplice le operazioni di addizione e sottrazione:
\[ (A+B)_{ij} = a_{ij} + b_{ij} \quad (A-B)_{ij} =a_{ij} – b_{ij} \]Data una matrice \(A(m,p)\) e una matrice \(B(p,n)\), allora è possibile definire anche il prodotto delle due matrici, che da come risultato una nuova matrice \(C(m,n)\), i cui elementi \(c_{ij}\) sono:
\[ c_{ij} = \sum_{k=1}^{p} a_{ik}b_{kj} \qquad 1\le i\le m \quad 1\le j\le n \]Se \(\lambda \in \mathbb{R}\) e \(A\) è una matrice con coefficienti \(a_{ij}\), allora indichiamo con \(\lambda A\) la matrice i cui coefficienti sono uguali a \(\lambda a_{ij}\).
La matrice identità, indicata con \(I_n\), è così definita:
Data una matrice \(A\), la matrice \(B\) è viene detta l’inversa di \(A\) se risulta \(AB=I\). La matrice ottenuta scambiando le righe con le colonne della matrice \(A\) si chiama la trasposta di \(A\), e viene indicata con il simbolo \(A^{T}\).
Date le matrici \(A\), \(B\), and \(C\) e un parametro reale \(\lambda\) si dimostrano facilmente le seguenti proprietà:
Per una matrice quadrata è possibile definire e calcolare il determinante, che è uno scalare, cioè un numero reale. Per la matrice unitaria \(I\) si ha \(det(I)=1\). Per una matrice quadrata \(A(2,2)\), il calcolo è semplice:
\[ det(A) = det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} = a_{11} a_{22} – a_{12} a_{21} \]Per una matrice \(A(3,3)\) il calcolo è più complesso; per ricordarlo può essere utile il seguente diagramma, che illustra la regola di Sarrus:
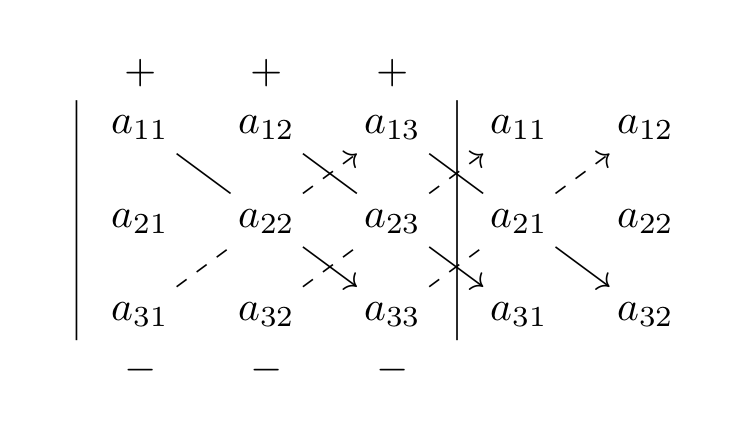
Quindi il determinante di una matrice \(A(3,3)\) è:
\[ \begin{align} det(A) = & \ a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ & \ – a_{13}a_{22}a_{31} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} \end{align} \]Il valore del determinante permette di determinare se le righe o le colonne di una matrice sono indipendenti fra loro. Inoltre è utile nella risoluzione dei sistemi di equazioni lineari. Un sistema di equazioni lineari di \(m\) equazioni ed \(n\) incognite è definito dalle seguenti equazioni:
\[ \begin{cases} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n & = b_1 \\ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n & = b_2 \\ & &\vdots \\ a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n & = b_m \end{cases} \]Il sistema può essere scritto in forma compatta come \(Ax = b\), dove \(A\) è la matrice \(m\times n\) con coefficienti \(a_{ij}\), \(x\) è il vettore colonna con coefficienti \(x_i\), e \(b\) è il vettore colonna con coefficienti \(b_i\).
Per uno studio approfondito delle operazioni sulle matrici, delle proprietà del determinante e della soluzione dei sistemi di equazioni lineari, vedere ad esempio [1].
2) Trasformazioni lineari
Le matrici vengono spesso utilizzate per trasformare un oggetto da uno spazio ad un altro. Una trasformazione lineare è una funzione
\[ T: \mathbb{R}^{n} \to \mathbb{R}^{m} \]tale che per tutti gli \(x,y\in \mathbb{R}^{n}\) e \(\lambda\in \mathbb{R}\):
\[ T(x+y) = T(x) + T(y) \quad T(\lambda x) = \lambda T(x) \]Se \(T:\mathbb{R}^{n} \to \mathbb {R}^{m}\) è una trasformazione lineare, \(x_1,\ldots,x_k\in \mathbb{R}^{n}\), e \(\lambda_1,\ldots,\lambda_k\in \mathbb {R}\), allora risulta:
\[ T(\lambda_1 x_1 + \cdots + \lambda_k x_k) = \lambda_1 T(x_1) + \cdots + \lambda_k T(x_k) \]Se \(\lambda\in R\) e \(S, T : \mathbb {R}^{n} \to \mathbb {R}^{m}\) sono due trasformazioni lineari, lo sono anche le seguenti \(S + T\) e \(\lambda T\) così definite:
\[ (S + T)(x) = S(x) + T(x)\qquad (\lambda T)(x) = \lambda (T(x))\quad x\in \mathbb {R}^{n} \]Ogni trasformazione lineare \(T\) può essere rappresentata tramite una matrice \(A\) e viceversa ogni matrice rappresenta una trasformazione lineare, tramite la relazione \(T(x) = Ax\), dove con il simbolo \(Ax\) si intende il prodotto della matrice \(A\) per il vettore \(x\).
3) Trasformazioni ortogonali e matrici ortogonali
Ricordiamo la definizione di prodotto scalare di due vettori \(x,y \in \mathbb{R}^{n}\):
\[ x\cdot y = x_{1}y_{1} + x_{2}y_{2} + … +x_{n}y_{n} \]La norma di un vettore \(x\), indicata con il simbolo \({\left| {x}\right|}\), può essere calcolata mediante il Teorema di Pitagora:
\[ {\left\| {x}\right\|}=\sqrt{x_{1}^{2} +x_{2}^{2} + .. +x_{n}^{2}} \]Una trasformazione ortogonale è una trasformazione lineare che preserva il prodotto scalare dei vettori e quindi preserva la distanza fra due punti. In formule abbiamo quindi:
\[ T(x) \cdot T(y) = x \cdot y \] \[ \Vert T(x) – T(y)\Vert = \Vert x- y\Vert \] \[ \Vert T(x) \Vert = \Vert x \Vert \]La matrice che rappresenta una trasformazione ortogonale viene chiamata matrice ortogonale ed ha le seguenti proprietà:
\[ A^{T}A = I \quad A^{T} = A^{-1} \]cioè la matrice trasposta coincide con la matrice inversa. Poiché il determinante della matrice trasposta di \(A\) è uguale a quello della matrice originale, abbiamo:
\[ det (A) \times det (A^{T}) = det (I) = 1 \quad \implies det (A) = \pm 1 \]Possiamo avere due casi distinti:
- \(det (A) = +1\) allora la matrice rappresenta una Rotazione
- \(det (A) = -1\) allora la matrice rappresenta una Riflessione
Nel piano una rotazione di un angolo \(\theta\) viene rappresentata da una matrice ortogonale \(A\) con \(det (A) = +1\):
\[ A = \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \]Un esempio di riflessione nel piano (\(det (A) = -1\)) è il seguente:
\[ A = \left( \begin{array}{cc} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array} \right) \]4) Matrici 4×4 e coordinate omogenee
Un’esigenza fondamentale nei videogiochi è quella di rappresentare la posizione degli oggetti, lo stato di rotazione e il fattore di scala delle tre dimensioni.
Le coordinate omogenee permettono di rappresentare tutte queste informazioni con un solo oggetto, una matrice 4×4. Si utilizzano 4 coordinate omogenee per rappresentare lo stato di un oggetto in ambiente 3D. Si può utilizzare una matrice ortonormale per la rotazione e, tramite le coordinate omogenee, ampliare la matrice da 3×3 a 4×4 per aggiungere le informazioni sulla posizione e la scala. Usiamo la notazione (x,y,z,w) per i vettori ,con le seguenti convenzioni:
- se \(w = 1\), allora il vettore \((x,y,z,1)\) rappresenta la posizione nello spazio
- se \(w = 0\), allora il vettore \((x,y,z,0)\) rappresenta una direzione
Matrici di traslazione
Una matrice di traslazione ha la seguente struttura:
\[ \left( \begin{array}{cccc} 1 & 0 & 0 & X \\ 0 & 1 & 0 & Y \\ 0 & 0 & 1 & Z \\ 0 & 0 & 0 & 1 \end{array} \right) \]dove \(X,Y,Z\) sono i valori che si vogliono aggiungere alla posizione.
Matrici per il cambiamento di scala
I parametri per il cambiamento di scala sono memorizzati nella diagonale. Le matrici hanno la seguente struttura:
\[ \left( \begin{array}{cccc} x & 0 & 0 & 0 \\ 0 & y & 0 & 0 \\ 0 & 0 & z & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]Ad esempio se si vuole scalare un vettore di \(3\) unità in tutte le direzioni, abbiamo:
\[ \left( \begin{array}{cccc} 3 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \cdot \left( \begin{array}{c} x \\ y \\ z \\ w \end{array} \right) = \left( \begin{array}{c} 3x \\ 3y \\ 3z \\ w \end{array}\right) \]mentre la coordinata \(w\) non cambia.
Matrici di rotazione
Una rotazione nello spazio 3D può essere espressa mediante \(3\) successive singole rotazioni, una intorno all’asse \(X\), un’altra all’asse \(Y\), e l’ultima intorno all’asse \(Z\).
Per una rotazione intorno all’asse x di un angolo \(\theta\):
Per una rotazione intorno all’asse y di un angolo \(\theta\):
\[ \left( \begin{array}{cccc} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]Per una rotazione intorno all’asse z di un angolo \(\theta\):
\[ \left( \begin{array}{cccc} \cos \theta & -\sin \theta & 0 &0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]Una sequenza di trasformazioni (ad esempio una traslazione seguita da una rotazione) è rappresentata da un matrice che si determina effettuando il prodotto delle matrici corrispondenti alle trasformazioni elementari. Quindi per effettuare un cambiamento di scala, una rotazione e una traslazione, basta moltiplicare le 3 matrici relative nell’ordine opposto:
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrixEsempio: sia data una rotazione di 30 gradi intorno all’asse x seguita da una traslazione \((1,-1,2)\) lungo gli assi x,y,z. La matrice corrispondente è:
\[ \left( \begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0\\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & \cos \theta & -\sin \theta & -1\\ 0 & \sin \theta & \cos \theta & 2 \\ 0 & 0 & 0 & 1 \end{array} \right) \]4.1) Svantaggi nell’utilizzo di matrici per rappresentare le rotazioni
Rappresentare le rotazioni con le matrici presenta tuttavia degli inconvenienti. In primo luogo sono necessari 16 numeri in virgola mobile per memorizzare i dati con le matrici 4×4. Le operazioni di arrotondamento sui numeri in virgola mobile causano una progressiva perdita della proprietà di ortogonalità delle matrici, con la conseguenza di avere effetti non desiderati di deformazioni o contrazioni.
Altri strumenti più efficienti per rappresentare e calcolare lo stato di rotazione di un oggetto 3D sono gli angoli di Eulero e i Quaternioni di Hamilton. Il teorema di Eulero afferma che, se un corpo rigido con un punto fisso, in un intervallo di tempo \(t\) passa da una configurazione iniziale \(C_{0}\) ad una finale \(C_{t}\), allora si può determinare una rotazione intorno ad un asse fissato che trasforma la posizione iniziale in quella finale.
Ogni rotazione può quindi essere descritta mediante i 3 angoli di Eulero, i quali specificano una successione di 3 successive rotazioni intorno agli assi cartesiani. La trasformazione complessiva può essere rappresentata con una matrice, ottenuta moltiplicando tra loro le matrici delle 3 singole trasformazioni.
Il framework Unity, insieme ad altri, utilizza gli angoli di Eulero e i Quaternioni di Hamilton per rappresentare le rotazioni ed effettuare i calcoli. Questi argomenti saranno oggetto studio in un prossimo articolo.
5) Matrici di proiezione
Per visualizzare una scena su uno schermo piatto 2D è necessario effettuare una trasformazione matematica, chiamata proiezione, che ad ogni oggetto immerso nella scena 3D fa corrispondere la sua immagine nello schermo 2D. Ci sono due tipi principali di proiezione:
- la proiezione prospettica
- la proiezione ortografica
Nella proiezione prospettica gli oggetti più lontani appaiono più piccoli; le linee parallele convergono in un punto chiamato punto di fuga. Nella proiezione ortografica gli oggetti appaiono della stessa dimensione, indipendentemente dalla distanza dalla telecamera. Rette parallele nello spazio 3D rimangono parallele anche nell’immagine proiettata.
Il tipo di proiezione da utilizzare dipende naturalmente dal tipo di gioco.
Si definisce ‘view frustum‘ il volume che contiene tutti i punti potenzialmente visibili sullo schermo. Questo volume dipende dalla disposizione dell’occhio della telecamera.
Se si utilizza la proiezione prospettica la forma del frustum è una piramide troncata. Nel caso della proiezione ortografica è un prisma rettangolare.
Il vertice della piramide corrisponde alla posizione della telecamera e la base della piramide viene chiamata il piano lontano (far plane).
Per definire il ‘view frustum’ si fissano due piani perpendicolari all’asse Z:
- il far plane
- il near plane
Questo due piani delimitano il campo visivo, che risulta limitato quindi dalle 6 superfici del tronco di piramide.
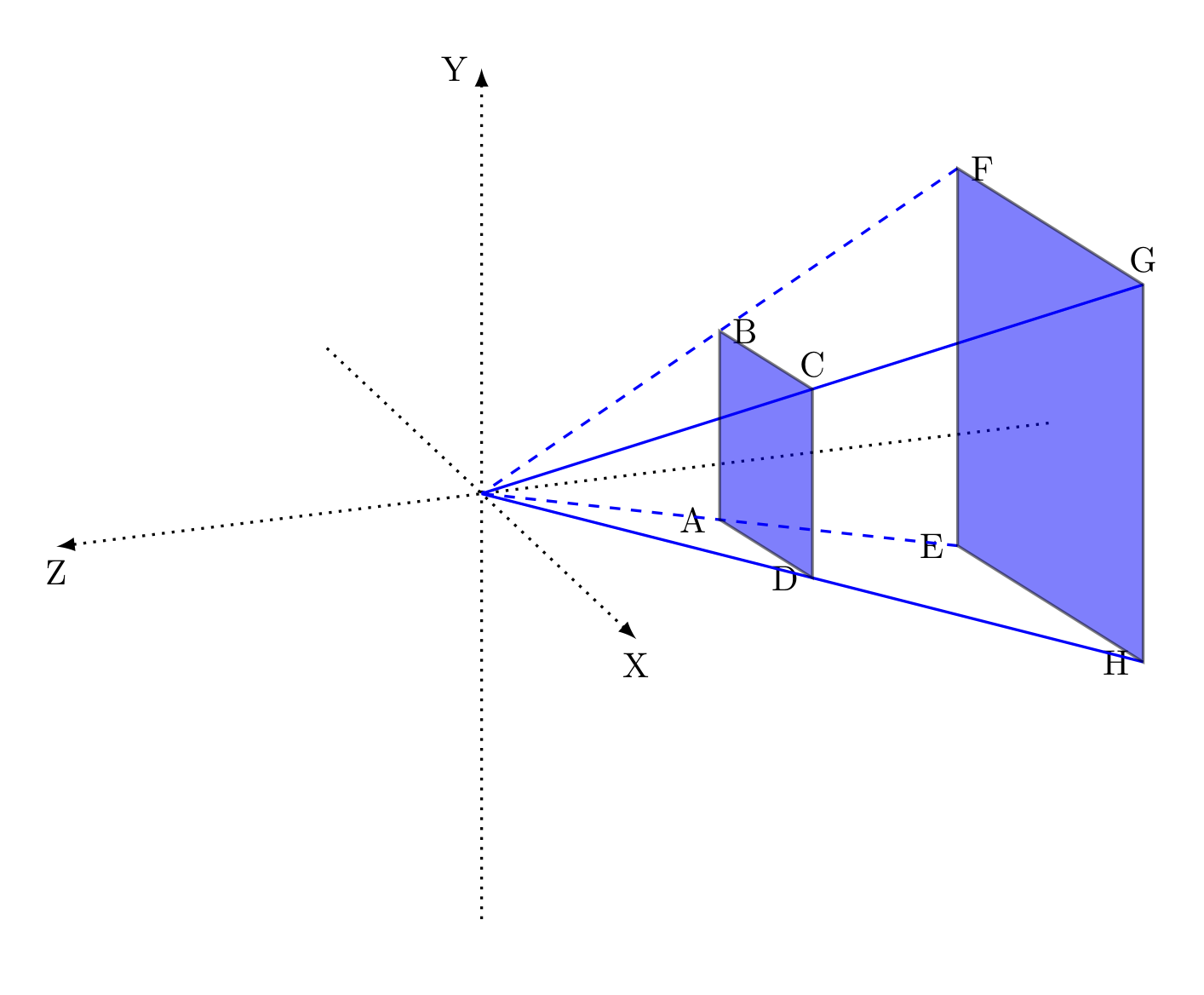
Il problema fondamentale da risolvere è quindi quello di proiettare gli oggetti presenti nella zona del ‘view frustum’ sullo schermo del device utilizzato per il gioco. Dal punto di vista matematico quindi si deve determinare la matrice 4×4 che rappresenta la proiezione prospettica o ortografica.
In realtà la trasformazione avviene in due fasi:
- trasformazione dei punti del view frustum in un cubo, chiamato homogeneous clip space, uno spazio intermedio indipendente dal tipo di proiezione utilizzato. Le coordinate omogenee delle spazio intermedio \([x,y,z,w]\) vengono inoltre normalizzate dividendo per \(w\): \([\frac{x}{w},\frac{y}{w},\frac{z}{w},\frac{w}{w}]\) (normalized device space (NDC));
- trasformazione del clip space nello screen space.
La determinazione della matrice di trasformazione permette di calcolare le coordinate delle immagini sullo schermo degli oggetti che stanno all’interno del ‘view volume’. Il calcolo delle matrici che permettono di effettuare le due proiezioni dalla scena 3D sullo schermo 2D è abbastanza complicato, e verrà descritto in un successivo articolo. In questa sede ci limitiamo a esporre le matrici.
Matrice per la proiezione prospettica
In base al diagramma del ‘view frustum’ sopra riportato, definiamo le coordinate dei vari punti:
\[ \{A=(l,b,-n); B=(l,t,-n); C=(r,t,-n); D=(r,b,-n) \} \] \[ \{E=(l,b,-f); F=(l,t,-f); G=(r,t,-f); H=(r,b,-f)\} \]dove i simboli hanno il seguente significato:
\[ \{l=left, r=right, b=bottom, t=top, n=near, f=far\} \]La matrice per la proiezione prospettica è la seguente:
\[ \left( \begin{array}{cccc} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 &\frac{2n}{t-b} &\frac{t+b}{t-b }& 0 \\ 0 & 0 & \frac{f+n}{f-n} & \frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{array} \right) \]Matrice per la proiezione ortografica
Con le stesse notazioni per i punti, abbiamo la seguente matrice:
\[ \left( \begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}; \\ 0 &\frac{2}{t-b} & 0 &-\frac{t+b}{t-b }\\ 0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n} \\ 0 & 0 & 0 & 1 \end{array} \right) \]Per uno studio approfondito delle matrici utilizzate nelle proiezioni vedere ad esempio [2].
6) Matrici e sistemi di coordinate in Unity
Per specificare la posizione di un oggetto nello spazio è necessario in primo luogo definire un sistema di riferimento (ad esempio un riferimento cartesiano). Quindi per ogni oggetto la posizione è determinata dalle sue tre coordinate relative al sistema di riferimento.
Ci sono diversi tipi di spazi di riferimento in Unity: lo spazio globale (world space), lo spazio locale (local space), il camera space, lo schermo (screen space) e il viewport (viewport space). In ogni spazio viene definito un sistema di coordinate per descrivere la posizione di ogni oggetto.
Nello spazio globale le coordinate di ogni oggetto sono riferite ad un punto fisso, l’origine. Lo spazio locale è definito relativamente ad un oggetto: l’origine è il centro dell’oggetto, che naturalmente può essere in movimento, e i vertici dell’oggetto sono definiti rispetto a questa origine locale. Nel Camera space le coordinate sono riferite rispetto alla posizione della telecamera, e quindi dell’osservatore. Nello screen space è definito un sistema di coordinate per identificare ogni punto dello schermo (UI coordinate), prendendo come origine \((0,0)\) il punto in basso a sinistra. Il Viewport ha un sistema di coordinate normalizzato, con le coordinate \((0,0)\) per il punto in basso a sinistra, e le coordinate \((1,1)\) per il punto in alto a destra.
Il componente Transform di Unity contiene informazioni molto importanti per ogni oggetto (GameObject) a cui appartiene, tra le quali:
- position – la posizione del gameObject (espressa con un Vector3)
- rotation – la rotazione (espressa come Quaternion)
- scale – il fattore di scala (sempre Vector3)
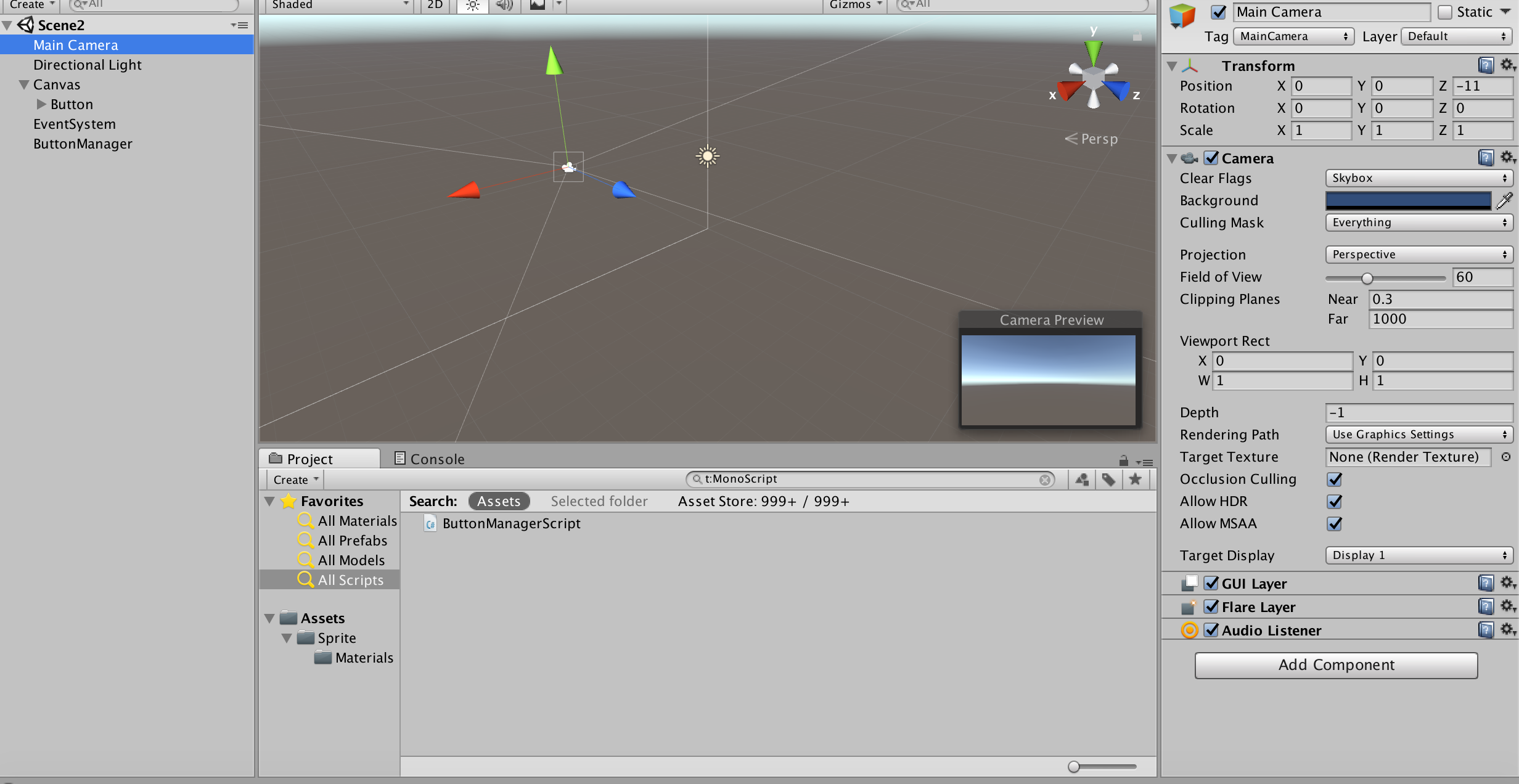
La posizione di un oggetto espressa con le coordinate di un dato tipo di spazio, può essere calcolata rispetto ad un altro spazio mediante una trasformazione lineare, cioè mediante una operazione algebrica sulle matrici. Unity mette a disposizione varie funzioni per passare da un sistema di coordinate ad un altro, ad esempio:
- TransformDirection
- TransformPoint
- TransformVector
- InverseTransformDirection
- InverseTransformPoint
- InverseTransformVector
Le prime tre effettuano una trasformazione dallo spazio locale a quello globale; le ultime tre fanno le trasformazioni inverse.
Ad esempio l’istruzione TransformDirection trasforma le coordinate di un vettore dallo spazio locale a quello globale.
Vector3 vettore = new Vector3 (1, 0, 0);
return transform.TransformDirection(vettore);Nello spazio globale il vettore \((1,0,0)\) si trova una unità a destra dell’origine del riferimento globale, mentre nello spazio locale il vettore è una unità a destra dell’oggetto, in base alla rotazione corrente dell’oggetto stesso.
Per convertire le coordinate di posizione di un oggetto dallo spazio locale a quello globale si può utilizzare la matrice localToWorldMatrix o viceversa la matrice worldToLocalMatrix.
Altre funzioni messe a disposizione da Unity sono le seguenti:
- Camera.WorldToScreenPoint
- Camera.WorldToViewportPoint
- Camera.ScreenToViewportPoint
- Camera.ScreenToWorldPoint
- Camera.ViewportToScreenPoint
- Camera.ViewportToWorldPoint
È evidente il ruolo fondamentale dell’algebra dei vettori e delle matrici in queste funzioni essenziali messe a disposizione dal framework Unity, come nelle analoghe di altri motori per videogiochi.
Conclusione
L’algebra delle matrici e le trasformazioni lineari sono strumenti indispensabili per manipolare gli oggetti geometrici e le immagini presenti sulla scena. Alcune matrici sono utilizzate per gestire i movimenti di traslazione e rotazione e i cambiamenti di scala delle dimensioni degli oggetti. Altre matrici permettono di gestire il rendering grafico, la colorazione e la proiezione dello spazio 3D sullo schermo a due dimensioni.
Il calcolo delle matrici è un argomento vasto e complesso. Per approfondire lo studio, oltre ai due testi già indicati, si può vedere anche questo: [3].
Bibliografia
[1]Seymour Lipschutz – Schaum’s Outline of Linear Algebra (MacGraw-Hill)
[2]Fletcher Dunn – 3D Math Primer for Graphics and Game Development (CRC Press)
[3]E. Lengyel – Foundations of Game Engine Development, Volume 1: Mathematics (Terathon Software LLC)

0 commenti