1) L’Aritmetica Modulare di Gauss
Dato un intero positivo \(m\), si dice che due interi \(a\) e \(b\) sono congruenti modulo \(m\) se danno lo stesso resto nella divisione per \(m\). Si usa la seguente notazione introdotta dal matematico tedesco Gauss:
\[ a \equiv b \pmod{m} \]Ad esempio \(21 \equiv 3 \pmod {9} \quad 100 \equiv 1 \pmod {33}\).
Vale la seguente proprietà.
Teorema 1.1
Sia fissato un intero non negativo \(m \in \mathbb{Z}\). Allora per ogni \(a \in \mathbb{Z}\), esiste un unico intero non negativo \(r\) tale che \(a \equiv r \pmod {m}\) e \(0 ≤ r < m\).
Si può dimostrare facilmente che la relazione di congruenza è una relazione di equivalenza (simmetrica, riflessiva e transitiva) e quindi induce una partizione dell’insieme degli interi \(\mathbb{Z}\) in \(m\) classi di equivalenza distinte. Un sistema completo di residui \(\pmod {m}\) è un insieme di \(m\) numeri distinti, ognuno preso da una delle \(m\) classi di equivalenza. La rappresentazione standard per le classi della congruenza modo m è formata prendendo come rappresentanti gli elementi dell’insieme {0,1,2, . . . ,m-1}.
Ad esempio se \(m=3\) abbiamo 3 classi di equivalenza, indicate con le parentesi quadre:
[0] che contiene gli interi \({-6,-3,0,3,6,9,..}\)
[1] che contiene gli interi \({-8,-5,-2,1,4,7,10,..}\)
[2] che contiene gli interi \({-7,-4,-1,2,5,8,11,..}\)
Si definiscono in modo naturale le operazioni di somma e prodotto fra due classi. L’insieme degli interi modulo \(m\) con le operazioni di somma e prodotto viene indicato con il simbolo \(\mathbb{Z}/(m)\).
Teorema 1.2
Se \(a \equiv b \pmod{m}\) e \(c \equiv d \pmod {m}\) allora:
Teorema 1.3
Se \((k,m)=1\), allora
Un settore importante della teoria dei numeri è lo studio delle equazioni alle congruenze, cioè equazioni del tipo \(f(x) \equiv b \pmod{m}\). Le soluzioni vengono considerate distinte solo se appartengono a classi di equivalenza diverse. Il caso più semplice è costituito dalle equazioni lineari alle congruenze , cioè equazioni del tipo: \(ax \equiv b \pmod{m}\). Questa equazione alle congruenze è equivalente alla equazione aritmetica \(ax-my=b\) che è risolubile in interi se e solo se \(d=(a,m)|b\). Questa proprietà è espressa nel seguente teorema.
Teorema 1.4
Se \((a,m)=d\), allora l’equazione \(ax \equiv b \pmod{m}\)
ammette soluzioni se e solo se \(d|b\).
Per quanto riguarda il numero delle soluzioni, vale il seguente:
Teorema 1.5
L’equazione lineare \(ax \equiv b \pmod {m}\), se \(d=(a,m)|b\) ha esattamente \(d\) soluzioni diverse (mod m).
Infatti se \(x_{0}\) è una soluzione, lo sono anche le seguenti
\[ \{x_{0} + \frac{m}{d},x_{0} + \frac{2m}{d},\cdots ,x_{0} + \frac{(d-1)m}{d}\} \]In particolare, la soluzione è unica se \(d=(a, m)=1\).
Si definisce l’inverso di a \(\pmod {m}\) un intero b tale che \( a · b \equiv 1 \pmod {m}\). Si usa la notazione \(a^{-1}\) oppure \([a]^{-1}\) per indicare l’inverso di a \(\pmod {m}\).
Dal teorema precedente segue che un inverso di a \(\pmod {m}\) esiste se e solo se \((a,m)=1\).
Esempio
Consideriamo l’equazione \(3x \equiv 18 \pmod {21}\). Abbiamo \(d=(3,21)=3\) e \(3|18\). Quindi esistono 3 soluzioni distinte. Una soluzione che si può facilmente trovare è \(x_{0}=6\): le altre due sono \(x_{1}= 6 + \frac{21}{3}=13\) e \(x_{2}= 6 + \frac {2 \cdot 21}{3}=20\).
1.1) Alcune semplici applicazioni
1.1.1) Il codice di Cesare
Il codice di Cesare è un semplice schema di crittografia, utilizzato da Giulio Cesare per comunicare con i suoi generali. Lo schema consiste nello spostare ogni lettera avanti di un numero fissato n di posti nell’alfabeto.
Ad esempio se \(n=4\) abbiamo lo schema seguente, supponendo di utilizzare l’alfabeto inglese di 26 lettere:
Quindi la parola ROMA viene codificata con la stringa VSQE.
Se associamo ad ogni lettera dell’alfabeto un numero da 0 a 25, il codice di Cesare equivale ad effettuare la somma modulo 26 del numero associato ad ogni lettera con la chiave segreta, costituita dal numero \(n\). Per l’operazione inversa di decrittazione basta effettuare la sottrazione modulo 26.
Naturalmente è un codice poco efficace. Il metodo di Vigenere è una variante più complessa del codice di Cesare; invece di spostare sempre dello stesso numero di posti la lettera da cifrare, questa viene spostata di un numero di posti variabile, determinato in base ad una parola chiave, rendendo più difficile decifrare il codice.
1.1.2) Criteri di divisibilità
Un’altra applicazione dell’aritmetica modulare è la dimostrazione dei criteri di divisibilità per i numeri interi.
Esempio (criterio divisibilità per 3)
Come è noto il criterio dice che un numero intero è divisibile per tre se e solo se la somma delle cifre è un numero divisibile per 3.
Ora, poiché \(10 \equiv 1 \pmod {3}\), moltiplicando entrambi i membri abbiamo:
\(100 \equiv 1 \pmod {3}; 1000 \equiv 1 \pmod {3}; 10000 \equiv 1 \ \pmod{3}\cdots\)
Considerato lo sviluppo decimale di n:
\(n=c_{k}\cdot 10^{k} + c_{k-1} \cdot 10^{k-1} \cdots +c_{1} \cdot 10 + c_{0}; \quad 0 \le c_{i} \le 9\)
possiamo sostituire tutte le potenze \(10^k\) con 1 ottenendo:
\(n \equiv (c_{k} + c_{k-1} \cdots +c_{1} + c_{0}) \pmod {3}\).
In modo analogo possono essere ottenuti per la divisibilità per 7, 9, 11.
2) Il Piccolo Teorema di Fermat
Il teorema di Fermat afferma che, se \(p\) è un numero primo e \(a\) un intero, allora:
\[ a^{p} \equiv a \pmod{p} \]È un caso particolare del teorema di Eulero, che vedremo in un prossimo articolo. Trova applicazioni importanti in vari settori della teoria dei numeri, in particolare per verificare se un intero è primo e anche nella crittografia a chiave pubblica.
Una formulazione equivalente è la seguente: se \(p\) è un numero primo e \(a\) è un intero non divisibile da \(p\), allora:
In realtà Fermat non diede una dimostrazione. Il teorema era già conosciuto anche da Gottfried Wilhelm Leibniz (1646-1716). La prima dimostrazione del teorema venne pubblicata da Eulero nel 1736. Si possono dare diverse dimostrazioni del teorema di Fermat.
2.1) Dimostrazione con la formula del binomio di Newton
Ricordiamo alcune definizioni. Il coefficiente binomiale \(\binom{n}{k}\), dove \(n,k\) sono interi positivi rappresenta il numero delle combinazioni semplici di \(n\) oggetti presi a \(k\) a \(k\); o in modo equivalente è il numero dei sottoinsiemi di ordine \(k\) che possono essere costruiti con il \(n\) oggetti. Si definisce anche \(\binom{n}{0} = 1\).
Si possono facilmente dimostrare le seguenti formule:
Se p è un numero primo, dalla formula precedente deriva che
\[ p | \binom{p}{k} \quad se \quad 0 < k < p; \]Vale inoltre il seguente teorema del binomio di Newton, che generalizza i prodotti notevoli del binomio e del trinomio che si insegnano nelle scuole elementari:
\[ (x+y)^n = \sum_{k=0}^n {n \choose k} x^{n – k} y^k \]Dai due teoremi precedenti deriva la seguente formula, utile per dimostrare il teorema di Fermat:
\[ (x+y)^p \equiv x^p +y^p \pmod{p} \]A questo punto abbiamo tutti gli strumenti per dimostrare il teorema di Fermat.
Dobbiamo dimostrare che \(a^{p} \equiv a \pmod{p}\), con p numero primo. Procediamo per induzione sul numero a. Se \(a=1\) l’affermazione è vera. Supponiamo ora che sia vera per un generico numero intero positivo \(a \ge 1\) e dimostriamo che è vera anche per \(a+1\). Applichiamo il teorema binomiale:
Poiché p divide tutti i termini del secondo membro, ad esclusione del primo e dell’ultimo, possiamo scrivere la seguente congruenza: \((a+1)^p \equiv a^p + 1 \pmod{p}\). Per l’ipotesi induttiva abbiamo quindi \((a+1)^p \equiv a+1 \pmod{p}\), come volevasi dimostrare.
2.2) Seconda dimostrazione
Una permutazione su un insieme di \(n\) elementi,che possiamo indicare con \({1, 2, . . . , n }\) oppure con le lettere \({a,b,c,…}\), è una corrispondenza biunivoca dell’insieme in se stesso. Precisamente è una funzione che ad ogni elemento dell’insieme ne associa un altro (eventualmente l’elemento stesso) in maniera che due elementi diversi non vengano mai associati ad uno stesso elemento. Le permutazioni possono essere rappresentate in forma esplicita utilizzando una matrice di due righe; ad esempio una permutazione sull’insieme \({1,2,3,4,5,6}\) è la seguente:
\[ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 3 & 5 & 6 & 1 & 4 \\ \end{pmatrix} \]Un tipo di permutazione importante è il ciclo, che sposta in modo ciclico alcuni elementi e tiene fissi gli altri. Ad esempio:
\[ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 3 & 5 & 1 \\ \end{pmatrix} \]Un ciclo può essere rappresentato anche con una singola riga, nella quale a ogni indice si associa quello successivo e all’ultimo si associa il primo: \(\{1,2,4,5\}\).
Si può dimostrare che qualunque permutazione può essere rappresentata in modo univoco come composizione di cicli disgiunti. Ad esempio la permutazione di cui sopra è equivalente alla composizione dei seguenti cicli: \(\{1,2,3,5\}\{4,6\}\).
Una permutazione si dice ciclica se può essere rappresentata con un solo ciclo. Per la dimostrazione del piccolo teorema di Fermat è utile il seguente teorema.
Teorema 2.1
Sia s una stringa arbitraria di lunghezza \(p\) simboli, non necessariamente tutti distinti, dove \(p\) è un numero primo. Se la stringa s contiene almeno due simboli diversi, allora le permutazioni cicliche di s sono tutte distinte.
Ad esempio data la stringa di numeri \(23411 \quad(p=5)\), le sue permutazioni cicliche sono \({34112, 41123, 11234, 12341}\). Invece nel caso della stringa \(2323 \quad(p=4)\) abbiamo \({3232, 2323, 3232}\) che non sono distinte, in quanto contengono sottostringhe uguali concatenate. Chiaramente questo non è possibile se la lunghezza è un numero primo.
Definiamo due stringhe equivalenti se ognuna può essere ottenuta dall’altra mediante una permutazione ciclica.
A questo punto possiamo dimostrare il teorema di Fermat. Prendiamo un insieme di \(n\) simboli e formiamo tutte le possibili stringhe di lunghezza \(p\), con ripetizioni. Il numero totale delle stringhe è uguale a \(n^p\). Togliendo le stringhe con lo stesso simbolo ci restano \(n^p – n\) stringhe. Ognuna di queste stringhe ha lunghezza p e ha quindi p permutazioni cicliche distinte. L’insieme delle \(n^p – n\) stringhe può essere quindi suddiviso in un numero finito di classi di stringhe; ogni classe contiene un gruppo di \(p\) permutazioni equivalenti. Questo implica che
dove \(k\) è il numero delle classi, e quindi il teorema è dimostrato.
2.3) Dimostrazione con il teorema di Burnside
Per introdurre il teorema di Burnside è utile ricordare la definizione di gruppo algebrico.
Un gruppo consiste in un insieme \(G\) sul quale è definita una operazione binaria \(\bullet\), cioè: \(\bullet : G \times G \rightarrow G\), tale che siano soddisfatte le seguenti proprietà:
1) \(a,b \in G \implies a\bullet b \in G\)
2) \(a,b,c \in G \implies a\bullet (b \bullet c) = (a \bullet b) \bullet c)\)
3) \( \exists e \in G\) tale che \(a \bullet e = e \bullet a = a \quad \forall a \in G\)
4) \( \forall a \in G \quad \exists b \in G\) tale che \(a\bullet b = b \bullet a = e\)
Un sottoinsieme H di G si dice sottogruppo se soddisfa tutte le proprietà di cui sopra con la stessa operazione binaria.
Un esempio di gruppo è l’insieme degli interi \(\mathbb{Z}\) con l’operazione di somma. L’elemento neutro è rappresentato dal numero \(0\).
Il gruppo simmetrico: indichiamo con \(S_{n}\) il gruppo di tutte le permutazioni sull’insieme \(X = {1,2,…n}\). L’operazione binaria di gruppo consiste nella composizione di due permutazioni. \(S_{n}\) viene chiamato il gruppo simmetrico degli \(n\) elementi, e la cardinalità dell’insieme è \(|S_{n}| = n!\). Ad esempio
Data una permutazione \(\sigma \in S_{n}, i \in \mathbb{N}\), definiamo la permutazione \(\sigma ^i \ge 0\), ottenuta componendo la \(\sigma\) con se stessa \(i\) volte; allora l’insieme \({\sigma ^i| i\ge 0}\) è il sottogruppo generato dalla permutazione \(\sigma\) e viene indicato con \(<\sigma>\).
Ricordiamo il concetto di simmetria. Una simmetria su un oggetto è un’operazione che trasforma un oggetto lasciando inalterato l’aspetto.
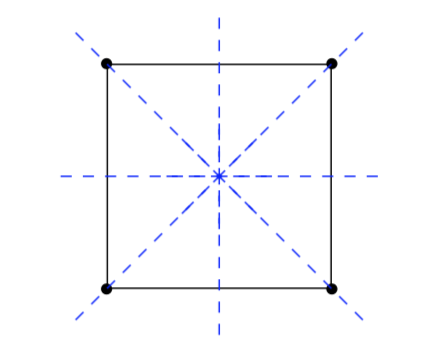
Come si vede dal diagramma precedente, il quadrato ha 8 simmetrie, 4 rotazioni e 4 riflessioni. In generale un poligono regolare di n lati ha 2n simmetrie.
Sia ora \(C\) un insieme di colori. Definiamo una colorazione come una funzione \(f\colon X \to C\) che assegna ad ogni elemento dell’insieme \(X={1,2,…n}\) un colore. Due colorazioni \(C_{1}\) e \(C_{2}\) si dicono equivalenti se esiste una simmetria \(\pi\) definita sul gruppo delle permutazioni tale che \(\pi (C_{1}) = C_{2}\). Tale relazione è una relazione di equivalenza e quindi l’insieme delle colorazioni è suddiviso in un numero finito di classi.
Il problema è come determinare le colorazioni diverse.Per ogni permutazione \(\pi\) indichiamo con \(\Psi (\pi)\) il numero delle colorazioni che rimangono invariate con \(\pi\).
Teorema 2.2 – Teorema di Burnside
Sia G un gruppo finito di permutazioni dell’insieme finito X. Sia Y un insieme di colorazioni chiuso rispetto a G. Allora il numero delle classi di equivalenza è:
dove \(\Psi (\pi) = \left\{ y \in Y \; | \; \pi(y)=y \right\}\).
Per una dimostrazione vedere ad esempio [1].
Per dimostrare il teorema di Fermat supponiamo che \(G\) sia il gruppo ciclico generato dalla permutazione \({1,2,..p}\). Le permutazioni in un gruppo ciclico possono esser interpretate anche come rotazioni dei vertici di un poligono regolare di p lati.
Supponiamo di avere \(n\) colori, e \(|G|=p\), dove p è un numero primo. Per ogni permutazione \(\pi\) dobbiamo calcolare \(\Psi(\pi)\).
Per la permutazione identità, che lascia invariati gli elementi, abbiamo il numero delle colorazioni invariate è \(n^{p}\). Per ognuna delle altre \(p-1\) permutazioni solo le colorazioni con un solo colore rimangono invariate, poiché p è un numero primo, quindi \((p-1) \cdot n\).
In definitiva, per il teorema di Burnside, abbiamo:
L’espressione finale rappresenta il numero delle colorazioni distinte e deve essere un intero positivo. Quindi \(n^p + (p-1)n\) deve essere divisibile per p. Semplificando abbiamo:
\[ n^p+(p-1)n \equiv 0 \pmod{p} \Rightarrow n^p-n\equiv 0 \pmod{p} \]e il teorema di Fermat è dimostrato.
2.4) Numeri pseudoprimi
Un numero intero composto \(n \ge 2\) si dice pseudoprimo rispetto alla base b se risulta \(b^{n-1} \equiv 1 \pmod{n}\).
Il più piccolo pseudoprimo n base \(2\) è \(341=11 \cdot 31\). Infatti risulta \(2^{340} \equiv 1 \pmod {341}\).
Si può dimostrare che per ogni base b esistono infiniti pseudoprimi rispetto alla base b.
Gli interi positivi composti m che sono pseudoprimi rispetto ad ogni base relativamente prima con m, sono detti numeri di Carmichael. Il più piccolo numero di Carmichael è
3) Alcuni esercizi da risolvere
1) Dimostrare che \(2^{35} + 1\) è divisibile per \(11\)
Osserviamo intanto che:
Quindi
\[ 2^{35} \equiv 5 \cdot 5 \cdot 7 \pmod{11} \]e quindi
\[ 2^{35} \equiv 3 \cdot 7 \pmod{11} \implies 2^{35} \equiv 10 \pmod {11} \]Sommando \(+1\) otteniamo infine: \(2^{35}+1 \equiv 0 \pmod{11}\).
2) Dimostrare la seguente formula:
\(x^{p-1} – 1 \equiv (x-1)(x-2) \cdots (x-(p-1)) \pmod{p}\)
Applicare il teorema di Fermat per tutti i valori di un sistema completo di residui, ad esempio \(\{0,1, \cdots p-1 \}\).
3) Dimostrare che \(341 | 20^{15}-1\).
Dimostrare che ognuno dei fattori primi di 341 divide il numero a destra.
4) Trovare il resto di \(605^{13} \div 7\).
Osserviamo che \(605 \equiv 3 \pmod{7}\). Quindi \(605^{13} \equiv 3^{13} \pmod{7}\).
Quindi abbiamo:
\(3^{13} = 3^{4} \cdot 3^{4} \cdot 3^{4} \cdot 3 \equiv 4 \cdot 4 \cdot 4 \cdot 3 \pmod{7} \implies 3^{13} \equiv 2 \cdot 5 \equiv 3 \pmod {7}\).
5) Calcolare \(2^{20} + 3^{30} + 4^{40} + 5^{50} + 6^{60} + 7^{70} \pmod{7}\).
Osserviamo che \( 2^6 \equiv 1 \pmod{7}\) e quindi
\(2^{20} = 2^{6} \cdot 2^{6} \cdot 2^{6} \cdot 2^{2} \equiv 4 \pmod{7}\).
Procedere in modo simile con le altre potenze. Alla fine si trova:
\(2^{20} + 3^{30} + 4^{40} + 5^{50} + 6^{60} + 7^{70} \equiv 4 + 1+4+4+1+0 = 14 \equiv 0 \pmod{7}\).
6) Dimostrare che se \(p\) è un numero primo, allora
\[ 1^{n-1} + 2^{p-1} +…. +(p-1)^{p-1} + 1 \equiv 0 \pmod{p} \]Applicare il Teorema di Fermat ai singoli elementi.
7) Dimostrare che per ogni intero positivo n il numero
\[ 3(1^{5}+2^{5}+ \cdots + n^{5}) \]è divisibile per il numero
\[ 1^{3}+2^{3}+ \cdots +n^{3} \]Calcolare, con il metodo di induzione, le formule per le somme delle potenze terze e delle potenze quinte.
8) Dimostrare che \(2^{70}+3^{70} \equiv 0 \pmod{13}\).
Partire da \(2^{12} \equiv 1 \pmod{13}\) e \(3^{3} \equiv 1 \pmod {13}\).
Per uno studio approfondito degli argomenti di questo articolo si possono consultare anche i seguenti testi: [2], [3], [4].
Bibliografia
[1]Tucker – Applied Combinatorics (Wiley)
[2]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991)
[3]Erdos, Suranyi – Topics in the theory of numbers (Springer)
[4]Hardy, Wright – An Introduction to the Theory of Numbers (Oxford University Press)
0 commenti