I Numeri Primi e la loro Distribuzione (III) – I Teoremi di Chebyshev

In un articolo precedente abbiamo studiato le congetture di Legendre e Gauss per descrivere il comportamento asintotico della funzione \(\pi(x)\), che conta il numero dei primi che non superano \(x\). In particolare ricordiamo la congettura di Gauss, che con notazione moderna è la seguente:

\[ \pi(x) \sim \int_{2}^{x}\frac{dt}{\ln t} \sim \frac{x}{\ln x} \]

Ricordiamo che il simbolo \(f(x) \sim g(x)\) significa che \(\lim_{x \to \infty}\dfrac{f(x)}{g(x)}=1\).

Le congetture proposte da Legendre e Gauss sono equivalenti al teorema dei numeri primi, tuttavia sono basate soprattutto su evidenze sperimentali. In questo articolo descriveremo i teoremi di Chebishev, che rappresentano un contributo matematico fondamentale nella direzione di una dimostrazione rigorosa del teorema dei numeri primi, che avverrà nel \(1896\) da parte dei matematici Hadamard e de la Vallée Poussin.

1) Ordine di grandezza delle funzioni aritmetiche

Lo studio del comportamento asintotico delle funzioni ha una importanza fondamentale in molti settori della matematica e nello studio della complessità degli algoritmi. Nella teoria dei numeri molte funzioni aritmetiche hanno un comportamento irregolare. Ad esempio la funzione \(d(n)\), che conta il numero dei divisori di un intero \(n\), assume il valore \(2\) su tutti i numeri primi; d’altra parte può assumere valori grandi a piacere, ad esempio \(d(2^{k})=k+1\), al tendere di \(k\) all’infinito. La funzione quindi non tende ad un valore definito al crescere di \(n\), ma oscilla indefinitivamente fra il valore minimo e valori grandi a piacere. Anche altre funzioni aritmetiche come la somma dei divisori \(\sigma(n)\) o la funzione di Eulero \(\varphi(n)\) hanno un comportamento irregolare.
In molti casi quindi è impossibile descrivere esattamente il comportamento di una funzione aritmetica \(f(n)\) per grandi valori di \(n\). Spesso è più utile studiare il comportamento della somma parziale

\[ S(n)= \sum\limits_{k=1}^{n}f(k) \]

oppure della media aritmetica

\[ S(n)=\frac{1}{n} \sum\limits_{k=1}^{n}f(k) \]

Introduciamo ora alcuni simboli speciali, proposti da Landau, Bachmann, Vinogradov e altri, per descrivere il comportamento asintotico delle funzioni.

1.1) Il simbolo O di Landau

Sia \(g(x)\) una funzione a valori reali positivi; la notazione

\[ f(x) = O(g(x)) \]

significa che esiste una costante positiva \(K > 0\) tale che

\[ |f(x)| \le K g(x) \ , \quad x \ge x_{0} \]

dove \(x_{0}\) è un numero reale opportuno.
Nella teoria dei numeri sono spesso usate anche le notazioni introdotte dal matematico russo Vinogradov:

\[ \begin{array}{l} f(x) \ll g(x) \iff f(x) = O(g(x)) \\ f(x) \gg g(x) \iff g(x) = O(f(x)) \\ f(x) \asymp g(x) \iff f(x) \ll g(x)\quad \text{e} \quad f(x) \gg g(x) \\ \end{array} \]

Esempio 1.1

\[ \begin{array}{l} f(x)= x^{3}+ 100x^{2}+ 2000 =O(x^{3}) \\ \sin x = O(1) \\ \dfrac{x}{x+1} = 1 + O\left(\dfrac{1}{x}\right) \\ \varphi(n) = O(n) \\ d(n) \le 2\sqrt{n} =O(\sqrt{n}) \end{array} \]

dove \(\varphi(n)\) è la funzione di Eulero e \(d(n)= \sum_{d|n}1\).

Esercizio 1.1
Dimostrare che

\[ \begin{array}{l} e^{\sqrt{\ln x}} =O(x) \\ \ln x = O(\ln \sqrt{x}) \end{array} \]

Esercizio 1.2
Dimostrare che

\[ f(x)=\sum\limits_{k=0}^{n}a_{k}x^{k} \implies f(x)=O(x^{n}) \]

Soluzione
Se \(x \ge 1\) allora

\[ |f(x)| \le \sum\limits_{k=0}^{n}|a_{k}|x^{k} \le \left(\sum\limits_{k=0}^{n}|a_{k}|\right)x^{n} \]

In generale, quindi, se \(f(x)\) è un polinomio di grado \(n\) il comportamento asintotico è determinato dal termine che ha il massimo grado.

Esercizio 1.3
Dimostrare che se \(f(x) \gt 0\) allora

\[ f(x)=O(g(x)) \implies \ln f(x) = O(\ln g(x)) \]

Esercizio 14
Dimostrare che se \(f(x) =O (g(x)\) con \(x \ge x_{0}\) allora

\[ \int_{x_{0}}^{x}f(t)dt = O \left(\int_{x_{0}}^{x}g(t)dt \right) \]

Esercizio 1.5
Dimostrare con un controesempio che in generale

\[ O(f(x))+O(g(x)) \neq O(f(x)+g(x)) \]

La notazione di Landau è molto utilizzata anche per stimare la complessità degli algoritmi in funzione dei dati di input.

Esercizio 1.6
Date due matrici quadrate \(n \times n\), dimostrare che il numero di moltiplicazioni e addizioni necessarie per calcolare la matrice prodotto con l’algoritmo ordinario è \(n^{2}(2n-1)\). La complessità dell’algoritmo è quindi \(O(n^{3})\).

1.2) Il simbolo \(o\)

Se \(\lim_{x \to \infty}\dfrac{f(x)}{g(x)}=0\) allora scriviamo

\[ f(x) = o(g(x)) \ , \quad x \to \infty \]

e diciamo che \(f(x)\) è trascurabile rispetto a \(g(x)\) per \(x \to \infty\).

Esempio 1.2

\[ \begin{array}{l} \sin x = o(x) \\ x^{n}= o(e^{x}) \\ \ln n = o(n^{\alpha}) \ , \quad \alpha \gt 0 \end{array} \]

1.3) Il simbolo \(\sim\)

Se \(\lim_{x \to \infty}\dfrac{f(x)}{g(x)}=1\) allora scriviamo

\[ f(x) \sim g(x) \ , \quad x \to \infty \]

e diciamo che \(f(x)\) è asintoticamente equivalente a \(g(x)\).

Esempio 1.3

\[ \begin{array}{l} \lfloor x \rfloor \sim x \\ 1000 + x^{2} \sim x^{2} \ , \quad x \to \infty \end{array} \]

Esercizio 1.7
Dimostrare che se \(f(x) \gt 0\) e \(g(x) \gt 0\), allora

\[ f(x) \sim g(x) \implies \ln f(x) \sim \ln g(x) \ , \quad x \to \infty \]

Esercizio 1.8
Dimostrare le seguenti relazioni

\[ \begin{array}{l} O(f(x)) \pm O(g(x)) = O (\text{max}(f(x),g(x))) \\ O(f(x)) \pm O(f(x)) = O(f(x)) \\ o(f(x)) + o(f(x))= o(f(x)) \\ O(f(x))\cdot o(f(x))= o(f^{2}(x)) \end{array} \]

Nota
Le definizioni date in precedenza considerano lo studio del comportamento di una funzione \(f(x)\) al crescere di \(x\), cioè per \(x \to \infty\). Tuttavia possono essere estese facilmente per studiare l’andamento di una funzione nell’intorno di un punto finito \(x_{0}\). Ad esempio è facile vedere che

\[ 1+ 100 x \sim e^{x} \ , \quad x \to 0 \]

1.4) Stima della somma armonica

Vediamo ora un’applicazione per la stima della somma armonica. In un articolo precedente abbiamo introdotto la costante di Eulero-Mascheroni:

\[ \gamma = \lim_{n \to \infty}\left(\sum\limits_{k=1}^{n}\frac{1}{k} – \ln n \right) \]

Il teorema seguente dà anche una stima dell’errore.

Teorema 1.1

\[ \sum\limits_{k=1}^{n}\frac{1}{k}= \ln n + \gamma + O\left(\frac{1}{n}\right) \]

dove \(\gamma \approx 0,57721 \) è la costante di Eulero-Mascheroni.

Dimostrazione
Indichiamo con \(\delta_{k}\) la differenza fra l’area della regione sottostante la curva \(f(x)=\dfrac{1}{x}\) nell’intervallo \([k-1,k]\), con \(k=2,3,\cdots\), e l’area del rettangolo inscritto. Nelle figura sotto, è l’area colorata in rosso.

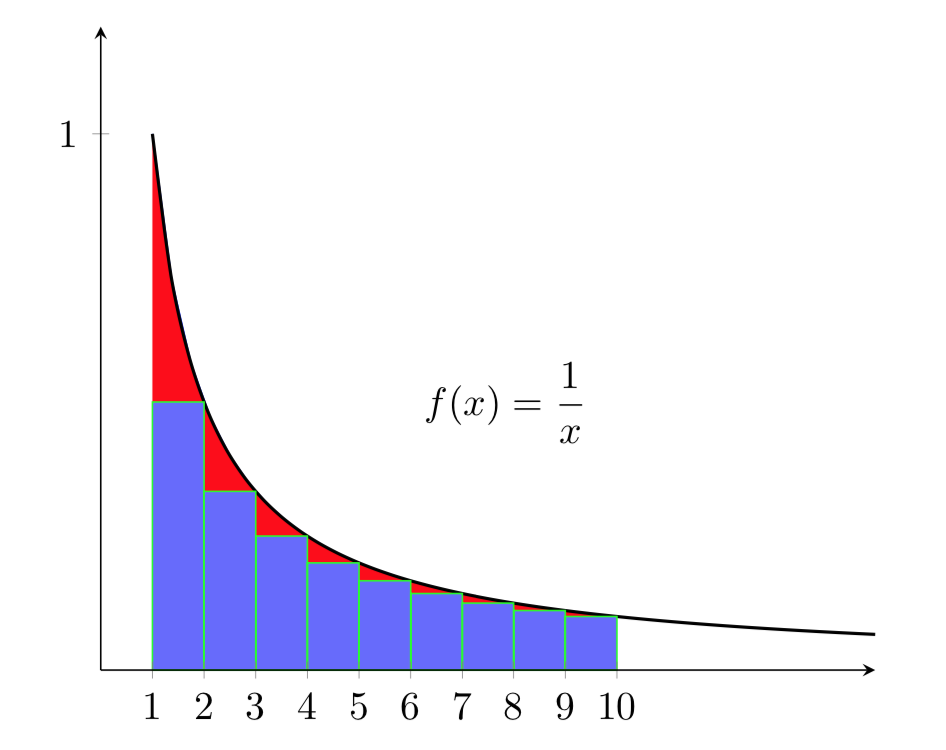
L’area \(\delta_{k}\) vale

\[ \delta_{k}= \ln k – \ln (k-1) – \frac{1}{k} \ , \quad k=2,3,\cdots \]

in quanto l’area sottostante la curva è uguale a \(\int\limits_{k-1}^{k}\dfrac{1}{t}dt=\ln k – \ln(k-1)\). Poniamo inoltre

\[ \gamma_{n}=\sum\limits_{k=1}^{n}\dfrac{1}{k}- \ln n=1-\sum\limits_{k=2}^{n}\delta_{k} \]

Ora il numero \(s_{n}=1-\gamma_{n}=\sum\limits_{k=2}^{n}\delta_{k}\) rappresenta la somma delle aree delle regioni colorate in rosso. Da semplici considerazioni geometriche si vede che risulta \(0 \lt s_{n} \lt \frac{1}{2}\) e inoltre

\[ s_{n}=1-\gamma_{n} \lt s_{n+1}=1-\gamma_{n+1} \]

La successione \(s_{n}\) è quindi limitata e crescente e da questo segue che esiste il limite per \(n \to \infty\). Chiamiamo tale limite \(1-\gamma\):

\[ \lim_{n \to \infty}s_{n}= \lim_{n \to \infty}(1-\gamma_{n})= 1-\gamma \]

Da questo segue che \(\lim_{n \to \infty}\gamma_{n}=\gamma\). Il resto della serie è quindi

\[ \gamma_{n}-\gamma=\sum\limits_{k=n+1}^{\infty}\delta_{k} \]

Questa serie infinita è costituita da regioni di area sempre più piccola al crescere di \(n\). Possiamo immaginare di traslare tutte queste regioni, senza sovrapposizioni fra loro, all’interno del rettangolo \(0 \le x \le 1\) e \(0 \le y \le \dfrac{1}{n}\). L’area complessiva delle regioni non può superare l’area \(\dfrac{1}{n}\) del rettangolo, quindi abbiamo \(\gamma_{n}-\gamma=O\left(\dfrac{1}{n}\right)\).

2) La formula di sommazione per parti di Abel

Un problema frequente nella teoria dei numeri consiste nel calcolare la somma parziale di una funzione aritmetica. Molto utile è la formula introdotta dal matematico norvegese Niels Henrik Abel (1802-1829). Si possono dare distinte formulazioni per il caso discreto e il caso continuo.

2.1) Il caso discreto

Sia \(a(n)\) una funzione aritmetica a valori reali o complessi, e poniamo

\[ A(n)=\sum\limits_{k=1}^{n}a(k) \ , \quad n \ge 1 \ , \quad A(0)=0 \]

Sia inoltre \(f(n)\) un’altra funzione aritmetica definita per \(n \ge 1\). Vale la seguente formula:

Teorema 2.1
Dati gli interi \(n > m \ge 0\) si ha:

\[ \sum\limits_{k=m+1}^{n}a(k)f(k)= \sum\limits_{k=m}^{n-1}A(k)(f(k)-f(k+1)) + A(n)f(n) – A(m)f(m) \]

Dimostrazione
La dimostrazione segue facilmente osservando che poiché \(a(k)=A(k)-A(k-1)\), possiamo scrivere

\[ \sum\limits_{k=m+1}^{n}a(k)f(k)= \sum\limits_{k=m+1}^{n}(A(k)-A(k-1))f(k) \]

Riordinando la somma a destra in base ai valori \(A(k)\) si arriva facilmente alla formula finale.
Nel caso importante \(m=0\), ricordando che \(A(0)=0\), la formula diventa

\[ \sum\limits_{k=1}^{n}a(k)f(k)= \sum\limits_{k=1}^{n-1}A(k)(f(k)-f(k+1)) + A(n)f(n) \]

2.2) Il caso continuo

Definiamo

\[ A(x)=\sum\limits_{k \le x}{}a(k) \ , \quad k \ge 1 \]

Supponiamo inoltre \(A(x)=0 \text{ se } x <1\).

Teorema 2.2
Sia \(f(t)\) una funzione con derivata continua nell’intervallo \([y,x]\), dove \(y >0\). Allora

\[ \sum\limits_{y\lt k \le x}{}a(k)f(k)= A(x)f(x) – A(y)f(y) -\int\limits_{y}^{x}A(t)f'(t)dt \]

Dimostrazione
Osserviamo che in un intervallo \([k,k+1)\) la funzione \(A(x)\) è costante e quindi \(A(x)=A(k)\) in tale intervallo. In ognuno di tali intervalli si ha

\[ \int\limits_{k}^{k+1}A(t)f'(t)dt= -A(k)(f(k)-f(k+1)) \]

Analoghe considerazioni valgono negli intervalli parziali iniziali e finali. Il teorema quindi può essere dimostrato a partire dal caso discreto.

Nel caso \(y=1\) la formula si semplifica:

\[ \sum\limits_{ k \le x}{}a(k)f(k)= A(x)f(x) -\int\limits_{1}^{x}A(t)f'(t)dt \]

Esercizio 2.1
Dimostrare le seguenti formule:

\[ \begin{array}{l} \sum\limits_{ k \le x}\dfrac{a(k)}{k}= \dfrac{A(x)}{x} + \displaystyle\int\limits_{1}^{x}\dfrac{A(t)}{t^{2}}dt \\ \sum\limits_{ k =1}^{n}\ln k = n \ln n -\displaystyle\int\limits_{1}^{n}\dfrac{\lfloor t \rfloor}{t}dt \end{array} \\ \]

dove \(\lfloor t \rfloor\) indica la parte intera del numero reale \(t\).

Mediante la formula di Abel si può dimostrare la seguente formula di sommazione di Eulero:

Teorema 2.3 – Eulero
Sia \(f(t)\) una funzione con derivata continua nell’intervallo \([y,x]\), dove \(y >0\). Allora

\[ \sum\limits_{y\lt k \le x}{}f(k)= \int\limits_{y}^{x}f(t)dt+ \int\limits_{y}^{x}(t -\lfloor t \rfloor)f'(t)dt + \\ \quad \quad f(x)(\lfloor x\rfloor -x)- f(y)(\lfloor y\rfloor -y) \]

Dimostrazione
In primo luogo osservare che, se \(a(n)=1\) per ogni \(n \ge 1\), allora \(A(x)=\left( x \right)\). Quindi utilizzare l’integrazione per parti per l’integrale \(\int\limits_{y}^{x}tf'(t)dt \).

Se \(y\) è un intero la formula diventa

\[ \sum\limits_{y\lt k \le x}{}f(k)= \int\limits_{y}^{x}f(t)dt+ \int\limits_{y}^{x}(t -\lfloor t \rfloor)f'(t)dt + f(x)(\lfloor x\rfloor -x) \]

Esercizio 2.2
Dimostrare che se \(m,n\) sono due interi e \(f(t)\) una funzione con derivata continua nell’intervallo \([m,n]\), allora

\[ \sum\limits_{k=m+1}^{n-1}f(k)= \int\limits_{m}^{n}f(t)dt+ \int\limits_{m}^{n}\left(t -\lfloor t \rfloor- \frac{1}{2}\right)f'(t)dt – \frac{1}{2}f(m) – \frac{1}{2}f(n) \\ \]

3) La funzione di Mangoldt

La funzione aritmetica di von Mangoldt \(\Lambda(n)\) è

\[ \Lambda (n)= \begin{cases} \ln p \quad \text { se } n=p^{k} \ , \quad k \ge 1 \\ 0 \quad \quad \text{ altrimenti} \\ \end{cases} \]

La funzione \(\Lambda (n)\) viene chiamata funzione di Mangoldt in onore del matematico tedesco Hans von Mangoldt (1854-1925). Alcuni valori della \(\Lambda(n)\) sono i seguenti:

\[ \Lambda(1)=0, \ \Lambda(2)=\ln 2, \ \Lambda(3)= \ln 3, \ \Lambda(10)=0 \]

Per un esame dei valori della funzione \(\Lambda(n)\) vedere il sito OEIS.

Teorema 3.1
Se \(n \ge 1\) allora

\[ \sum\limits_{d|n} \Lambda(d) = \ln n \]

Dimostrazione
Supponiamo \(n=\prod\limits_{i=1}^{r}p_{i}^{a_{i}}\). Prendendo il logaritmo abbiamo

\[ \ln n = \sum\limits_{i=1}^{r}a_{i}\ln p_{i} \]

Ma \(p_{i}^{k}|n\) se e solo se \(1 \le k \le a_{i}\), quindi i soli termini non nulli della funzione \(\Lambda(d)\) sono i divisori della forma \(p_{i}^{s}\) con \(s=1,2,\cdots, a_{i}\) e \(i=1,2,\cdots, r\). Perciò abbiamo

\[ \sum\limits_{d|n}{}\Lambda(d)=\sum\limits_{i=1}^{r} \sum\limits_{s=1}^{a_{i}}\ln p_{i}= \sum\limits_{i=1}^{r}a_{i}\ln p_{i} = \ln n \]

La funzione di Mangoldt è strettamente correlata con la funzione zeta di Riemann, introdotta per primo da Eulero (limitatamente al caso reale) nel suo fondamentale teorema del prodotto:

\[ \zeta(s) =\sum\limits_{n=1}^{\infty}\frac{1}{n^{s}}=\prod\limits_{p}^{}\frac{1}{\left(1- p^{-s}\right)} \ , \quad s \gt 1 \]

Vale infatti il seguente teorema:

Teorema 3.2

\[ \frac{\zeta’(s)}{\zeta(s)}= -\sum\limits_{n=1}^{\infty}\frac{\Lambda(n)}{n^{s}} \quad s \gt 1 \]

Dimostrazione
Prendendo il logaritmo nella formula di Eulero abbiamo

\[ \ln \zeta(s) =\sum\limits_{p} \ln \left(\frac{1}{1-p^{-s}}\right) \]

Possiamo differenziare la serie termine a termine in quanto \(s \gt 1\), ottenendo

\[ \frac{\zeta’(s)}{\zeta(s)}= -\sum\limits_{p}\frac{\ln p}{p^{s}-1} = -\sum\limits_{p}\ln p\sum\limits_{k=1}^{\infty}p^{-ks} \]

Poiché la doppia serie è assolutamente convergente per \(s \gt 1\), possiamo raggruppare i termini in qualsiasi modo senza cambiare la somma della serie. Quindi

\[ \frac{\zeta’(s)}{\zeta(s)}= -\sum\limits_{p,k} p^{-ks} \Lambda(p^{ks}) = -\sum\limits_{n=1}^{\infty}\frac{\Lambda(n)}{n^{s}} \]

4) Le funzioni di Chebyshev

Introduciamo altre due funzioni aritmetiche che hanno un ruolo fondamentale nello studio della distribuzione dei numeri primi:

\[ \begin{array}{l} \theta (x) = \sum\limits_{p \le x} \ln p \\ \psi (x) = \sum\limits_{n \le x} \Lambda (n) \\ \end{array} \]

Le funzioni \(\theta(x)\) e \(\psi(x)\) vengono chiamate funzioni di Chebyshev, in onore del matematico russo Chebyshev (1821-1894).

Esercizio 4.1
Dimostrare che

\[ \psi (x) = \sum\limits_{n=1}^{\infty} \theta (x^{1/n})= \sum\limits_{n \le \log_{2}x}{} \theta (x^{1/n}) \]

La sommatoria è in realtà finita, in quanto \(\theta(x^{1/n})=0\) se \(x^{1/n} \lt 2\).

Teorema 4.1
Per \(x \ge 2\) si ha

\[ \begin{align} \theta (x)= \pi(x) \ln x – \int\limits_{2}^{x} \frac{\pi(t)}{t} dt \tag{A}\\ \pi (x)= \frac{\theta(x)}{\ln x} + \int\limits_{2}^{x} \frac{\theta(t)}{t \ln^{2}t} dt \tag{B}\ \end{align} \]

Dimostrazione
Applichiamo la formula di sommazione di Abel con \(y=1\). Indichiamo con \(a(n)\) la funzione caratteristica dei numeri primi, cioè \(a(n)=1\) se \(n\) è un numero primo, altrimenti \(a(n)=0\). Quindi \(\pi(x)=\sum\limits_{ 1 \lt n \le x }a(n)\). Come funzione \(f(x)\) prendiamo \(f(x)=\ln x\). Per la formula di Abel abbiamo

\[ \sum\limits_{1 \lt n \le x}a(n)\ln n = \pi(x)\ln x – \pi(1)\ln 1 – \int\limits_{1}^{x}\frac{\pi(t)}{t}dt \]

Poiché \(\theta(x)=\sum\limits_{1 \lt n \le x}a(n)\ln n \), la formula \((A)\) è dimostrata.
Per dimostrare la formula \((B)\) definiamo \(b(n)=a(n)\ln n \), \(f(x)=\dfrac{1}{\ln x}\). Osserviamo che \(\theta(x)=\sum\limits_{n \le x} b(n)\). Utilizzando la formula di Abel con \(y= 3/2\) abbiamo

\[ \sum\limits_{3/2 \lt n \le x}\frac{b(n)}{\ln n} = \frac{\theta(x)}{\ln x} – \frac{\theta(3/2)}{\ln 3/2} + \int\limits_{3/2}^{x}\frac{\theta(t)}{t\ln^{2}t}dt \]

Poiché \(\pi(x)= \sum\limits_{3/2 \lt n \le x}\dfrac{b(n)}{\ln n}\) la formula \((B)\) è dimostrata, in quanto \(\theta(t)=0\) se \(t \lt 2\).

Teorema 4.2
Al tendere di \(x \to \infty\) si ha

\[ \begin{align} \frac{\theta (x)}{x}= \frac{\pi (x)}{x / \ln x} + o(1) \tag{A}\\ \frac{\psi (x)}{x}= \frac{\pi (x)}{x / \ln x} + o(1) \tag{B} \end{align} \]

Dimostrazione
Poiché sappiamo che \(\dfrac{\pi(t)}{t}=o(1)\), cioè \(\lim_{t \to \infty}\dfrac{\pi(t)}{t}=0\), (vedi articolo su questo sito) risulta

\[ \int\limits_{2}^{x}\frac{\pi(t)}{t}dt=o(x) \]

e quindi

\[ \frac{\theta(x)}{x}= \frac{\pi(x)}{x / \ln x} + o(1) \]

Per la formula \((B)\) ricordiamo che per l’esercizio 4.1

\[ \psi (x) = \theta(x) + \theta(x^{\frac{1}{2}})+ \theta(x^{\frac{1}{3}})+ \cdots \]

Il termine \(x^{1 /n}\) si annulla per \( n \ge \dfrac{\ln x}{\ln 2}\). Quindi il numero dei termini non nulli è dell’ordine \(O(\ln x)\). Poiché \(\theta(t) \le \sum_{n \le t}\ln t\le t \ln t\), abbiamo

\[ \theta(x^{1 / k}) \lt x^{1 / k}\ln x \le x^{1 / 2}\ln x \]

e quindi

\[ \psi(x) – \theta(x) =O(x^{1 / 2}(\ln x)^{2}) \]

Per dimostrare la formula \((B)\) sostituiamo la \(\theta(x)\) con la \(\psi(x)\) nella formula \((A)\). L’errore dell’ordine \(O(x^{- 1 / 2}(\ln x)^{2})\) viene assorbito nell’errore infinitesimo \(o(1)\) in quanto

\[ \lim_{x \to \infty}\frac{(\ln x)^{2}}{x^{1 / 2}}=0 \]

5) I teoremi di Chebyshev

Il matematico russo Chebyshev riuscì a determinare l’ordine di grandezza della funzione \(\pi(x)\), dimostrando che esistono due costanti positive \(c_{1},c_{2}\) tali che

\[ \begin{array}{l} c_{1}\dfrac{x}{\ln x} \lt \pi(x) \lt c_{2}\dfrac{x}{\ln x} \ , \quad \quad x \gt x_{0} \end{array} \]

per tutti i numeri reali maggiori di un dato \(x_{0}\). Chebyshev diede anche dei valori approssimati per le due costanti

\[ c_{1} \approx 0,9212 \ , \quad c_{2} \approx 1,1055 \]

In questo paragrafo dimostriamo vari teoremi che ci permetteranno di arrivare al risultato di Chebyshev. Il prossimo teorema fornisce una maggiorazione dall’alto della funzione \(\theta(x)\).

Teorema 5.1

\[ \theta (n) \le 2n \ln 2=n\ln 4 \]

Dimostrazione
Dimostriamo per induzione su \(n\). Il teorema è vero per \(n=1,2\). Supponiamo che sia vero per tutti gli interi \(k \le n-1\) e dimostriamo che è vero anche per \(k=n\).  Se \(n\) non è primo, allora

\[ \theta(n)=\theta(n-1) \le 2(n-1)\ln2 \le 2n\ln2 \]

per l’ipotesi induttiva. Supponiamo ora che \(n\) sia un primo dispari \(n=2m+1\). Sappiamo che il coefficiente binomiale

\[ \binom{2m+1}{m}= \frac{(2m+1)!}{m!(m+1)!} \]

è divisibile da tutti i numeri primi \(p\) tali che \(m+2 \le p \le 2m+1\).
Ora i due coefficienti binomiali \(\binom{2m+1}{m}\) e \(\binom{2m+1}{m+1}\) sono uguali e sono presenti nell’espansione binomiale di \((1+1)^{2m+1}\). Quindi abbiamo

\[ \binom{2m+1}{m} + \binom{2m+1}{m+1} \le 2^{2m+1} \]

da cui segue, essendo i due coefficienti binomiali uguali,

\[ \binom{2m+1}{m} \le 2^{2m} \]

Mettendo insieme i risultati abbiamo

\[ \theta(2m+1)-\theta(m)=\ln \prod\limits_{m+2\le p\le 2m+1}p \le\ln 2^{2m}=2m \ln 2 \]

Per l’ipotesi induttiva \(\theta(m+1)\le 2(m+1) \ln2\) e quindi

\[ \theta(2m+1) \le 4m \ln2 \le 2(2m+1) \ln 2 \]

Teorema 5.2
Dimostrare che

\[ e^{\psi(n)}=[1,2,\cdots,n] \]

dove \([1,2,\cdots,n]\) è il minimo comune multiplo dei numeri in parentesi.

Dimostrazione
Osserviamo che la scomposizione fattoriale del minimo comune multiplo può essere scritta nel seguente modo:

\[ [1,2,\cdots,n]=\prod\limits_{p}p^{a_{p}} \]

dove \(a_{p}\) è la massima potenza di \(p \le n\). Il valore di \(a_{p}\) è il seguente:

\[ a_{p}=\Big\lfloor \frac{\ln n}{\ln p}\Big\rfloor= \sum\limits_{p^{\alpha}\le n}1 \]

Da questo segue il teorema, in quanto

\[ e^{\psi(n)}=e^\left({\sum_{p^{\alpha} \le n}\ln p}\right) \]

Il prossimo teorema fornisce una maggiorazione dal basso della funzione \(\psi(x)\).

Teorema 5.3

\[ \psi (2n+1) \ge 2n \ln 2 \]

Dimostrazione
Consideriamo il seguente integrale:

\[ I = \int\limits_{0}^{1}x^{n}(1-x)^{n}dx \]

L’integrale si pò calcolare mediante lo sviluppo binomiale di Newton \((1-x)^{n}=\sum\limits_{k=0}^{n}\binom{n}{k}(-1)^{k}x^{k}\):

\[ I = \sum\limits_{k=0}^{n}\binom{n}{k}\frac{(-1)^{k}}{n+k+1} \]

Quindi l’integrale è un numero razionale, inoltre il prodotto \(I \cdot[1,2,\cdots,2n+1]\) è un intero. Perciò dal teorema precedente

\[ e^{\psi(2n+1)}I \ge 1 \]

Nell’intervallo \([0,1]\) la funzione \(f(x)=x(1-x)\) ha un massimo nel punto \(x=\dfrac{1}{2}\) dove vale \(\dfrac{1}{4}\). Da questo deriva che l’integrale \(I \le \dfrac{1}{4^{n}}\).
Dalla relazione precedente abbiamo

\[ e^{\psi(2n+1)} \ge 2^{2n} \]

Prendendo i logaritmi abbiamo infine

\[ \psi(2n+1) \ge 2n \ln 2 \]

Dai teoremi precedenti e dal teorema 4.3 segue il teorema di cui sotto:

Teorema 5.4
Le funzioni \(\theta(x)\) e \(\psi(x)\) sono dell’ordine della funzione \(f(x)=x\); cioè esistono delle costanti \(A,B,C,D\) tali che

\[ \begin{array}{l} Ax \lt \theta(x) \lt Bx \\ Cx \lt \psi(x) \lt Dx \\ \end{array} \]

Queste relazioni possono essere scritte in forma compatta mediante la simbologia di Vinogradov:

\[ \begin{array}{l} \theta(x) \asymp x \\ \psi(x) \asymp x \\ \end{array} \]

A questo punto possiamo dimostrare il teorema fondamentale di Chebyshev.

Teorema 5.5 – Chebyshev
Esistono due costanti positive \(c_{1},c_{2}\) e un numero reale positivo \(x_{0}\) tali che

\[ \begin{array}{l} c_{1}\dfrac{x}{\ln x} \lt \pi(x) \lt c_{2}\dfrac{x}{\ln x} \ , \quad x \ge x_{0} \end{array} \]

Dimostrazione
Ricordiamo le relazioni dimostrate in precedenza

\[ \begin{array}{l} \theta(x) \le 2x \ln 2 \\ \psi(2n+1) \ge 2n \ln 2 \end{array} \]

Dalla definizione di \(\theta(x)\) abbiamo

\[ \begin{array}{l} \sum\limits_{\sqrt{x} \lt p \le x} \ln p \le 2x \ln 2 \end{array} \]

Da questa segue

\[ \begin{array}{l} (\pi(x) -\pi(\sqrt{x})) \ln x \le 4 x \ln 2 \\ \pi(x) \le \pi(\sqrt{x}) + \dfrac{4x \ln 2}{\ln x} \end{array} \]

Poiché ovviamente \(\pi(\sqrt{x}) \le \sqrt{x}\) abbiamo

\[ \begin{array}{l} \pi(x) \le \pi(\sqrt{x}) + \dfrac{4x \ln 2}{\ln x} = O\left(\dfrac{x}{\ln x}\right) \end{array} \]

in quanto \(\lim_{x \to \infty}\dfrac{\ln x}{x^{1/2}}=0\).
Per la stima inferiore ricordiamo la formula dimostrata in precedenza (teorema 4.2):

\[ \psi(x) – \theta(x) =O(x^{1 / 2}(\ln x)^{2}) \]

Poiché \(\psi(x) \gg x\) si ha anche \(\theta(x) \gg x \). Ragionando come sopra abbiamo

\[ \begin{array}{l} \sum\limits_{\sqrt{x} \le p \le x} \ln p + O(\sqrt{x}\ln x) \gg x \end{array} \]

Da questa relazione segue a maggior ragione che \(\pi(x)\ln x \gg x\) per \(x\) abbastanza grande.

Una ulteriore conseguenza del teorema di Chebyshev è che se la funzione \(\dfrac{\pi(x)}{x/\ln x}\) tende ad un limite quando \(x \to \infty\), allora tale limite è uguale a \(1\). Introduciamo la funzione

\[ T(x)=\sum_{1 \le n \le x}\ln n \]

Teorema 5.6
Per \(x \ge 2\) si ha

\[ T(x) = x \ln x – x + O(\ln x) \]

Dimostrazione
Definiamo \(N=\lfloor x \rfloor\). Calcoliamo i seguenti integrali:

\[ \begin{array}{l} I_{1}= \int\limits_{1}^{N}\ln t dt = N\ln N – N+1 \\ I_{2}= \int\limits_{1}^{N+1}\ln t dt = (N+1)\ln (N+1) – (N+1) + 1 \end{array} \]

La funzione \(\ln x \) è crescente per \(x > 0\) e quindi

\[ \ln n \le \int\limits_{n}^{n+1}\ln t dt \le \ln (n+1) \]

Da questo segue

\[ I_{1} \le T(x)=\sum\limits_{n \le x}\ln n \le I_{2} \]

Da questo segue poi il teorema in quanto sia \(I_{1}\) sia \(I_{2}\) sono \(=x \ln x – x + O(x)\).

Teorema 5.7

\[ T(x) = \sum\limits_{n \le x}\psi \left(\frac{x}{n}\right) \ , \quad x \gt 1 \]

Dimostrazione
Ricordiamo che \(\psi(x)=\sum_{n \le x}\Lambda(n)\) e \(\sum_{d|n}\Lambda(d)=\ln n\). Abbiamo

\[ \begin{array}{l} \sum\limits_{n \le x}\psi\left(\dfrac{x}{n}\right) = \sum\limits_{n \le x}\sum\limits_{m \le x/n}\Lambda(m)= \\ \sum\limits_{mn \le x}\Lambda(m)= \sum\limits_{n \le x}\sum\limits_{m |n}\Lambda(m)= \\ \sum\limits_{n \le x}\ln n= T(x) \end{array} \]

Dai teoremi precedenti deriva la seguente stima:

\[ T(x)=\sum\limits_{n \le x}\psi\left(\frac{x}{n}\right) \sim x \ln x \ , \quad x \to \infty \]

Ricordiamo ora le definizioni di minimo limite e massimo limite di una successione di numeri. Sia \(a_{n}\) una successione di numeri reali. Definiamo i seguenti simboli:

\[ \begin{array}{l} s_{n}= \inf \{a_{k}: k \ge n\} \\ S_{n}= \sup \{a_{k}: k \ge n\} \\ \end{array} \]

dove i simboli \(\inf\) e \(\sup\) indicano rispettivamente l’estremo inferiore e l’estremo superiore degli insiemi di numeri.
E’ facile verificare che le successioni \(s_{n}\) e \(S_{n}\) sono monotone, la prima crescente e la seconda decrescente, quindi esistono i limiti

\[ \begin{array}{l} l = \lim\limits_{n \to \infty} s_{n} \\ L = \lim\limits_{n \to \infty}S_{n} \end{array} \]

I due limiti si chiamano rispettivamente il minimo limite e il massimo limite della successione iniziale \(a_{n}\) e vengono indicati con i simboli \(\liminf a_{n}\) e \(\limsup a_{n}\). Si usano anche i nomi limite inferiore e limite superiore.

Esempio 5.1
Data la successione \(a_{n}=(-1)^{n}\) si ha \(\liminf a_{n}=-1\) e \(\limsup a_{n}=+1\). Non esiste invece il limite ordinario della successione.

Esercizio 5.1
Calcolare il minimo e massimo limite delle seguenti successioni:

\[ \begin{array}{l} \displaystyle a_{n}= \sin \dfrac{n \pi}{3} \\ \displaystyle a_{n}= n^{\left(\sin \dfrac{n \pi}{2}\right)} \end{array} \]

Una successione \(a_{n}\) può non avere il limite ordinario. Tuttavia il limite inferiore e quello superiore esistono sempre.

Teorema 5.8
Il limite di una successione \(a_{n}\) esiste se e solo se \(\liminf a_{n}= \limsup a_{n}\) e in tal caso ha lo stesso valore.

I concetti di limite inferiore e superiore possono essere estesi in modo naturale anche al caso delle funzioni.
Il seguente teorema di Chebyshev afferma che se esiste il limite \(\lim_{x \to \infty}\dfrac{\pi(x)}{x / \ln x}\) allora tale limite è uguale a \(1\).

Teorema 5.9 – Chebyshev

\[ \lim \inf_{x \to \infty}\dfrac{\psi(x)}{x} \le 1 \le \lim\sup_{x \to \infty}\dfrac{\psi(x)}{x} \]

Dimostrazione
Diamo solo uno schema della dimostrazione. Indichiamo con \(l,L\) il minimo e il massimo limite della funzione \(\dfrac{\psi(x)}{x}\), per \(x \to \infty\). Dalla definizione di minimo limite segue che

\[ \psi(x) \ge lx + h(x) \]

dove \(h(x)=o(x)\), cioè \(\lim_{x \to \infty}\dfrac{h(x)}{x}=0\). Quindi

\[ \begin{array}{l} \sum\limits_{n \le x}\psi\left(\dfrac{x}{n}\right)\ge lx \sum\limits_{n \le x}\dfrac{1}{n}+ \sum\limits_{n \le x}h\left(\dfrac{x}{n}\right) = \\ lx \ln x + o(x \ln x) + \sum\limits_{n \le x}h\left(\dfrac{x}{n}\right)= lx \ln x + o(x \ln x) \end{array} \]

dove l’ultimo passaggio si giustifica facilmente ricordando la relazione della somma armonica (teorema 1.1). Per il teoremi 5.6 e 5.7 deve essere \( l \le 1\).
Con un ragionamento simile si dimostra che \(L \ge 1\).

Da questo teorema e dal teorema 4.2 segue che, se esiste il limite \(\lim_{x \to \infty}\dfrac{\pi(x)}{x / \ln x}\), allora tale limite deve essere uguale a \(1\).
Questo risultato è molto importante, in quanto fissa dei limiti superiore e inferiore per la distribuzione dei numeri primi. Tuttavia per completare la dimostrazione del teorema dei numeri primi è necessario dimostrare che il limite esiste. Si tratta di un problema molto difficile, di cui lo stesso Chebyshev era ben consapevole.

6) Il postulato di Bertrand

Un altro risultato importante di Chebyshev è la dimostrazione della congettura di Bertrand (1822-1900), secondo la quale per ogni intero positivo \(n \) esiste almeno un numero primo \(p\) tale che

\[ n \lt p \le 2n \]

Per la dimostrazione completa vedere l’articolo su questo sito.
In questo paragrafo dimostriamo il seguente risultato:

Teorema 6.1
Esiste un numero reale \(K\) tale che, per ogni \(x \ge 1\), esiste un numero primo \(p\) che soddisfa

\[ x \lt p \le Kx \]

Dimostrazione
In precedenza abbiamo dimostrato che le funzioni \(\theta(x),\psi(x)\) hanno lo stesso ordine della funzione \(f(x)=x\). Quindi esistono esistono delle costanti \(A,B\) tali che

\[ \begin{array}{l} Ax \lt \theta(x) \lt Bx \ , \quad x \ge 2 \end{array} \]

Da questo segue

\[ \begin{array}{l} \theta\left(\dfrac{Bx}{A}\right) \gt A\left(\dfrac{Bx}{A}\right) = Bx \gt \theta(x) \end{array} \]

Questa relazione implica che esiste almeno un numero primo nell’intervallo compreso fra \(x\) e \(\dfrac{Bx}{A}\). Per la dimostrazione del teorema possiamo prendere \(K=\max\left(\dfrac{B}{A},2\right)\).

Un risultato simile è il seguente teorema, dimostrato nel \(1891\) da Chebyshev e Sylvester (1814-1897).

Teorema 6.2 – Chebyshev-Sylvester
Per tutti gli \(x\) sufficientemente grandi esiste almeno un numero primo \(p\) tale che

\[ x \lt p \lt (1+\alpha)x \]

dove \(\alpha \approx 0,092\) viene chiamata costante di Chebyshev-Sylvester.
Il teorema dei numeri primi afferma che questa relazione è vera per ogni \(\alpha \gt 0\).

Concludiamo l’articolo con le parole di Sylvester che rendono omaggio all’importanza dei risultati ottenuti da Chebyshev:

“Chebyshev was the only man ever able to cope with the refractory character and erratic flow of prime numbers and to confine the stream of their progression with algebraic limits.”

Conclusione

I risultati di Chebyshev hanno rappresentato un importante progresso nella conoscenza della distribuzione dei numeri primi. Per completare il lavoro restava da dimostrare che effettivamente esiste il limite della funzione \(\dfrac{\pi(x)}{x/\ln x}\). Si tratta di un problema alquanto difficile. La dimostrazione sarà resa possibile grazie ai nuovi strumenti messi a disposizione dal matematico tedesco Bernhard Riemann (1826-1866), mediante i suoi studi sulle proprietà della funzione zeta estesa al campo complesso.

---

Bibliografia

^[1]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers (V edition; Wiley, 1991).

^[2]W. LeVeque – Fundamentals of Number Theory (Dover)

^[3]Hardy, Wright – An Introduction to the Theory of Numbers (Oxford University Press)

^[4]S. Miller, R. Takloo-Bighash – An Invitation to Modern Number Theory (Princeton U.P.)

^[5]G. Tenenbaum, M. Mendes France – The Prime Numbers and Their Distribution (American Mathematical Society)