Un numero primo è un intero maggiore di 1 che è divisibile solo da 1 e da se stesso. Un numero intero che non è primo si dice composto. Ogni intero maggiore di 1 è divisibile da almeno un numero primo. Lo studio dei numeri interi e delle loro proprietà è iniziato con i Greci (Pitagora, Euclide,…), e i loro importanti risultati sono in gran parte riportati nell’opera di Euclide (gli ‘Elementi‘).
La Teoria dei Numeri è la branca della matematica che studia le proprietà dei numeri primi e degli interi. L’importanza e la bellezza della Teoria dei Numeri è rappresentata in modo efficace con le le parole di Gauss (1777-1855), il principe dei Matematici: “La matematica è la regina delle scienze, e la teoria dei numeri è la regina della matematica“. Gauss ha avuto un ruolo fondamentale nello sviluppo della Teoria dei Numeri. Nella sua opera ‘Disquisitiones arithmeticae‘, scritta in latino e in seguito tradotta nelle principali lingue[1], ha riassunto in modo sistematico i risultati dei periodi precedenti, ha introdotto le moderne notazioni, e ha posto una serie di risultati e riflessioni che hanno indirizzato lo studio dei matematici nei decenni successivi.
Un’opera fondamentale per lo studio della storia della Teoria dei Numeri, a partire dall’antichità, è la seguente: [2]. Per una interessante panoramica dello stato attuale della Teoria dei Numeri vedere [3].
Nel seguito riportiamo alcuni dei risultati più significativi riguardanti la Teoria dei Numeri.
1) Il Teorema fondamentale dell’Aritmetica
Ogni intero \(n>1\) può essere scritto in modo univoco nella forma
\[ n=p_1^{a_1}p_2^{a_2}p_3^{a_3}…p_s^{a_s} \]dove \(s\) è un intero positivo, gli \(a_j\) sono interi positivi e \(p_1,p_2,\dotsc,p_s\) sono numeri primi che soddisfano la relazione \( p_1 < p_2 < \dotsb < p_s.\)
La dimostrazione si trova in ogni testo elementare di Teoria dei Numeri. Ad esempio vedere [4].
La validità del teorema può sembrare ovvia a prima vista. Tuttavia esistono molti altri insiemi di numeri sui quali è definita l’operazione di moltiplicazione, con la proprietà associativa e commutativa, per i quali non vale l’unicità della fattorizzazione. Un esempio classico è quello fornito dal matematico tedesco David Hilbert(1862-1943); i numeri appartenenti all’insieme di Hilbert sono i naturali del tipo \(4n+1, n\in \mathbb{N}\), cioè i numeri seguenti:
\[ 1,5,9,13,17,21,25,29,33,…. \]Ogni numero di Hilbert è primo oppure è il prodotto di numeri primi (I primi di Hilbert non coincidono con i primi normali; ad esempio 21 è un primo di Hilbert).
Esercizio
Dimostrare, fornendo almeno un esempio, che la fattorizzazione dei numeri di Hilbert non è unica.
2) Teorema – L’insieme dei numeri primi è infinito
Riportiamo la dimostrazione che si trova negli Elementi di Euclide. Supponiamo per assurdo che esistano solo n numeri primi \(p_1, p_2, …,p_n\), con \(n\) intero positivo. Definiamo l’intero \(Q=p_1p_2…p_n+1\). Come ogni intero \(Q\) ha almeno un divisore primo, indicato con \(q\). Ora supponiamo che \(q=p_i\) per qualche \(1\leq i\leq n\). Allora il numero \(q\) dividerebbe \(p_1p_2…p_n\) e anche la differenza \(Q-p_1p_2…p_n\). Questo implicherebbe che \(q\) divide \(1\), chiaramente non possibile.
Esistono numerose altre diverse dimostrazioni del teorema. Come esempio riportiamo la dimostrazione di Stieltjes (1890): sia dato un qualunque insieme finito di numeri primi \(p_{1}, p_{2}, …{p_k}\) il cui prodotto sia \(x = p_{1}p_{2}..p_{k}\). Sia \(ab\) una qualunque fattorizzazione del prodotto \(x\): cioè \(x=ab\). Allora ognuno dei numeri \(p_{i}\) divide a oppure b, ma on divide entrambi. Quindi nessuno dei \(p_{i}\) divide la somma \(a+b\). Quindi deve esistere almeno una altro numero da aggiungere all’insieme originale.
3) Il crivello di Eratostene
Due problemi di fondamentale importanza sono i seguenti:
- fattorizzazione: dato un intero positivo n, trovare la sua scomposizione in fattori primi
- test di primalità: dato un intero positivo n, riconoscere se è un numero primo
L’importanza di questi problemi è stata sottolineata da Gauss nella sua opera fondamentale con le seguenti parole: “The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic“[5]
Il crivello di Eratostene è un semplice ed efficace algoritmo ideato dal matematico greco Eratostene (276 – 194 a.c.) per individuare tutti i numeri primi minori di un fissato numero intero positivo.
In primo luogo osserviamo che il numero 2 è primo (l’unico numero primo pari). Quindi eseguiamo i seguenti passi:
– scrivere la lista di tutti i numeri interi maggiori di 1 fino al numero più grande numero n che si vuole verificare;
– togliere dalla lista tutti i multipli del primo numero (la prima volta saranno i multipli di 2). Il primo numero rimasto nella lista è un numero primo;
– ripetere il passo precedente fino a che non ci sono più multipli dei numeri primi che sono minori di n.
In realtà l’algoritmo si può limitare ad eliminare i multipli minori di \(\sqrt{n}\) in quanto è facile dimostrare che se n è un numero composto, allora ha un fattore primo che non supera \(\sqrt{n}\). Infatti se \(n\) è composto, allora \(n=ab \), dove a,b sono interi tali che \( 2 \leq a,b\) con \(a\leq b\). Se fosse \(a > \sqrt{n}\), allora \(\sqrt{n} < a \leq b\) e come risultato \( ab > n \).
L’algoritmo di Eratostene è semplice e facile da implementare con un programma; tuttavia per valori molto grandi di n diventa poco efficiente, anche con i computer più potenti.
La possibilità di utilizzare computer sempre più potenti e lo sviluppo di algoritmi molto sofisticati permette oggi di fattorizzare numeri interi con molte cifre (>100).
4) Il Teorema dei numeri primi
La distribuzione dei numeri primi è stata oggetto di studio da parte dei matematici fin dall’antichità. Il teorema fondamentale, intravisto da Legendre e Gauss, è stato dimostrato quasi contemporaneamente nel 1896, dai matematici Hadamard e de la Vallée Poussin. Indichiamo con \(\pi(n)\) il numero dei numeri primi \(\leq n\). Allora vale il seguente teorema:
\[ \lim_{n\to\infty}\frac{\pi(n)}{n/\log(n)}=1 \]dove \(\log(n)\) è il logaritmo naturale di \(n\).
La dimostrazione di questo teorema è alquanto complessa. Il grande matematico norvegese Abel definì questo come il più importante teorema di tutta la Matematica. Per una dimostrazione “elementare” vedere [6], oppure per una dimostrazione che utilizza i metodi dell’analisi complessa vedere [7].
La distribuzione dei numeri primi è estremamente irregolare. Ad esempio fra due numeri primi consecutivi possono esistere distanze grandi a piacere. Vale infatti il seguente:
Teorema
Dato un intero positivo \(n\) grande a piacere, esistono \(n\) interi composti consecutivi.
Per dimostrarlo basta considerare la successione di interi positivi: (n+1)!+2, (n+1)!+3,…,(n+1)!+n, (n+1)!+n+1. Ognuno di questi interi è un numero composto in quanto \(k\) divide \((n+1)!+k\) se \(2\leq k\leq n+1\) .
5) La funzione zeta di Riemann e la formula di Eulero
Eulero (1707-1783) è stato uno dei più grandi matematici di tutti i tempi ed ha dato contributi fondamentali in molto settori della Matematica, in particolare nella Teoria dei numeri. Una formula importante scoperta e dimostrata da Eulero è la seguente:
\[ \displaystyle\sum_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6}. \]Oltre alla bellezza intrinseca di questa formula, notiamo il ruolo misterioso del numero \(\pi\), irrazionale e trascendente, che risulta somma di una serie calcolata sulle potenze inverse di numeri interi.
La funzione
dove \(s\) è un numero reale o complesso è la famosa funzione zeta di Riemann, che ha un ruolo importante in molti campi della Matematica, e soprattutto nella Teoria dei Numeri. Il collegamento con i numeri primi è dato dalla seguente Formula di Eulero:
\[ \sum_{n=1}^\infty\frac{1}{n^s} = \prod_{p \text{ primo}} \frac{1}{1-p^{-s}} \]dove il prodotto a destra si estende su tutti i numeri primi \(p\).
6) L’ipotesi di Riemann
Il matematico tedesco Bernhard Riemann (1826-1866), nonostante la sua breve vita, ha dato contributi importanti e rivoluzionari in molti campi della Matematica. I suoi risultati relativi alla Geometria differenziale Riemanniana sono stati fondamentali per una nuova concezione della geometria dello spazio fisico e per lo sviluppo della Teoria della Relatività Generale di Albert Einstein. Nel campo della Teoria dei Numeri l’opera principale di Riemann è rappresentata dal suo breve, ma molto importante articolo pubblicato nel 1859: “Ueber die Anzahl der Primzahlen unter einer gegebenen Grosse” (Sul numero di numeri primi al di sotto di una certa grandezza).
Nel suo studio Riemann esamina le proprietà della funzione zeta
estendendo la definizione anche a valori complessi della variabile \(s\). Questa funzione è analitica il tutto il piano complesso, ad eccezione del punto \(s=1\).
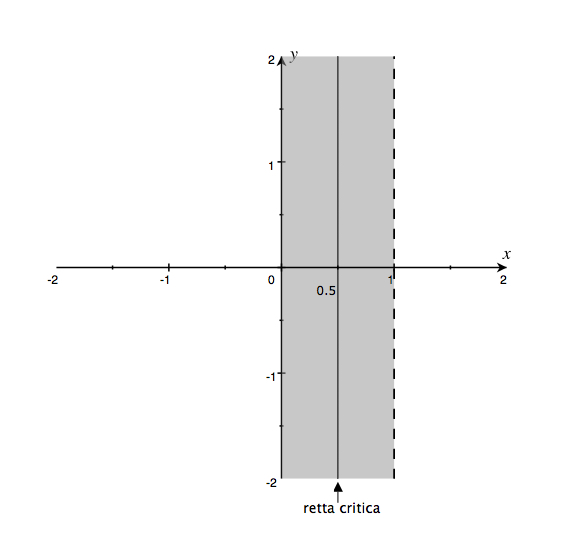
La funzione zeta non ha zeri nella regione dove la parte reale di \(s\) è maggiore o uguale a uno. Nella regione con parte reale di \(s\) minore o uguale a zero la funzione zeta assume il valore zero negli interi negativi pari \(\{-2,-4,-6,…\}\); questi zeri vengono chiamati gli zeri banali. Tutti gli zeri rimanenti stanno nella striscia con parte reale di \(s\) compresa fra 0 e 1(la cosiddetta striscia critica).
È stato dimostrato che esistono infiniti zeri nella striscia sulla retta \(s=1/2+iy\) con \(y\) che assume valori reali; questa retta si chiama la retta critica. L’ipotesi di Riemann afferma che tutti gli zeri non banali della funzione zeta si trovano nella retta critica.
Ad oggi tutti gli zeri non banali sono stati trovati sulla retta critica. Tramite i computer sono state fatte verifiche su un numero grandissimo di zeri. Tuttavia la congettura di Riemann rimane uno dei più difficili e non risolti problemi della Matematica.
Per uno studio approfondito della funzione Zeta e dell’ipotesi di Riemann vedere [8], oppure [9].
7) La congettura di Goldach
La congettura venne proposta nel 1742 da Christian Goldbach (1690-1764) ad Eulero. Esistono due versioni della congettura. La congettura forte di Goldbach afferma che ogni numero pari maggiore di 2 è somma di 2 numeri primi. La congettura debole afferma che ogni numero dispari maggiore di 5 è somma di 3 numeri primi. La congettura forte implica quella debole ma non viceversa.
Esempi: \(30 = 17 + 13\); \(33 = 3 + 17 + 13\);
Allo stato attuale la congettura non è stata dimostrata, ma sono stati fatti importanti progressi.
Il matematico russo Schnirelmann (1930) ha dimostrato il seguente teorema: esiste un numero intero N tale che ogni numero da un certo punto in poi può essere scritto come somma di al massimo N numeri primi.
Il matematico russo Vinogradov (1937) ha dimostrato che ogni numero dispari da un certo punto in poi può essere scritto come somma di 3 numeri primi.
Il matematico cinese Chen (1966) ha dimostrato che ogni intero pari sufficientemente grande può essere scritto come somma di un numero primo ed un altro numero che ha al massimo due fattori primi.
Nel 2013 il matematico peruviano Harald Helfgot ha pubblicato una possibile dimostrazione della congettura debole. Tuttavia, data la complessità della dimostrazione, sarà necessaria una revisione della comunità dei matematici, prima di poter essere accettata.
Per uno studio approfondito della teoria additiva dei numeri vedere [10].
8) Applicazioni alla crittografia
Il problema della fattorizzazione degli interi ha trovato importanti applicazioni nel campo della crittografia dei dati, fondamentale con la diffusione di internet. Esistono due tipi principali di algoritmi crittografici:
- algoritmi simmetrici che usano la stessa chiave per le operazioni di codifica e decodifica
- algoritmi asimmetrici che usano due chiavi diverse per le due operazioni
Gli algoritmi simmetrici richiedono che sia il mittente che il destinatario conoscano la chiave comune. Questo rappresenta un limite fondamentale per le moderne trasmissioni di dati, che avvengono tramite le reti di computer fra tutte le parti del mondo.
Gli algoritmi asimmetrici prevedono per ogni utente due chiavi: una pubblica e una privata. La chiave pubblica può essere registrata in un database pubblico accessibile a tutti, mentre la chiave privata deve restare segreta. L’informazione crittografata con una chiave pubblica può essere decodificata solo con la chiave privata associata. Il più famoso algoritmo di crittografia simmetrica è l’algoritmo RSA, sviluppato nel 1977 da Ron Rivest, Adi Shamir e Leonard Adleman. La sicurezza dell’algoritmo RSA, su cui si basa la crittografia a chiave pubblica, è basata sulla difficoltà di fattorizzare numeri interi con un numero molto grande di cifre (> 200).
Per uno studio approfondito sul legame fra Teoria dei Numeri e Crittografia vedere [11].
Conclusione
La teoria dei numeri è la branca più vecchia della matematica pura, e anche la più vasta. Ci sono ancora molti problemi non risolti, tra i quali i più famosi sono la congettura di Goldbach e l’ipotesi di Riemann. Tuttavia ne esistono molti altri interessanti, riguardanti i numeri primi e le loro proprietà, le relazioni fra numeri, gli insiemi di numeri con proprietà particolari, le configurazioni di particolari sequenze di numeri, ecc.). Molti di questi problemi hanno una facile formulazione ma la loro soluzione risulta spesso difficilissima o quasi impossibile. Nonostante possano apparire problemi slegati dalla realtà, attraggono comunque l’interesse di molti matematici. Possiamo concordare con l’affermazione del grande matematico Jacobi (1804 – 1851): “Scopo della scienza è l’onore dello spirito umano e, da questo punto di vista, una questione di teoria dei numeri vale tanto quanto una relativa al sistema del mondo“.
Bibliografia
[1]C. F. Gauss – Disquisitiones Arithmeticae (Springer-Verlag, 1985)
[2]Dickson – History of the Theory of Numbers, Vol. 1-2-3 (Chelsea Publishing Company, N.Y., 1971)
[3]Jay Goldman – The Queen of Mathematics (AK Peters, 1988)
[4]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991), pag. 20
[5]C. F. Gauss – Disquisitiones Arithmeticae (Springer-Verlag, 1985), pag. 396
[6]Hardy-Wright – An Introduction to the Theory of Numbers, V edition (Oxford, 1979), pag. 340-373
[7]T. Apostol – Introduction to Analytic Number Theory (Springer, 1976), pag. 278-290
[8]Edwards – Riemann’s Zeta Function (Academic Press, 1974)
[9]Titchmarsh – The Theory of the Riemann Zeta Function (Oxford Science Publications, 1996)
[10]M. Nathanson – Additive Number Theory (Springer GTM, 1996)
[11]N. Koblitz – A Course in Number Theory an Crytography (Springer GTM, 1994)
0 commenti