Successioni di Numeri Reali e Complessi: Studio della Convergenza e Calcolo dei Limiti

Nella prima parte di questo articolo studieremo le successioni di numeri reali. Introdurremo il concetto di limite, che è la base del calcolo differenziale e integrale. Nella seconda parte analizzeremo anche le successioni di numeri complessi. Al fine di assimilare questi concetti, per nulla banali, vengono proposti diversi esercizi e problemi.

1) I numeri reali

Nel corso del secolo XIX sono stati definiti in modo rigoroso i numeri reali e il concetto di limite, che sono alla base del calcolo differenziale e integrale. La definizione rigorosa dei numeri reali ha permesso di stabilire delle basi solide per l’analisi matematica, rendendola indipendente da qualsiasi considerazione geometrica.
L’insieme dei numeri reali è costituito dall’unione dei numeri razionali e dei numeri irrazionali. Dedekind (1831-1916) diede una definizione dei numeri reali, a partire dai numeri razionali, utilizzando dei metodi algebrici. Un’altra, equivalente, definizione venne data da Cantor (1845-1918).
Per definire i numeri irrazionali Dedekind introdusse il concetto di sezione sui numeri razionali. Indichiamo con \(\mathbb{Q}\) l’insieme dei numeri razionali.

Definizione 1.1
Una partizione dei numeri razionali in due sottoinsiemi \(A,B\) non vuoti è una sezione se:

• \( A \cup B = \mathbb{Q}\) e \( A \cap B = \emptyset\)
• tutti gli elementi di \(A\) sono minori di tutti gli elementi di \(B\)
• l’insieme \(A\) non contiene un elemento maggiore di tutti gli altri

Indichiamo una sezione con il simbolo \((A,B)\).

Esempio 1.1
Ogni numero razionale \(x\) determina un’unica sezione di Dedekind. Ad esempio se \(x=2\) abbiamo:

\[ \begin{array}{l} A = \{x \in \mathbb{Q}: x \lt 0\} \cup \{x \in \mathbb{Q}: x \ge 0; x \lt 2\} \\ B = \{x \in \mathbb{Q}: x \ge 2\} \end{array} \]

Tuttavia esistono anche sezioni che non sono generate da numeri razionali.

Esempio 1.2
Il numero irrazionale \(\sqrt{2}\) è definito dalla seguente sezione:

\[ \begin{array}{l} A = \{x \in \mathbb{Q}: x \lt 0\} \cup \{x \in \mathbb{Q}: x \ge 0; x^{2} \lt 2\} \\ B = \{x \in \mathbb{Q}: x \ge 0; x^{2} \ge 2\} \end{array} \]

Quindi mediante il concetto di sezione possiamo rappresentare sia i numeri razionali sia i numeri irrazionali. Ogni sezione di Dedekind rappresenta un numero reale. L’insieme dei numeri reali è indicato con il simbolo \(\mathbb{R}\).
Per quanto riguarda la continuità (o completezza) della retta reale Dedekind propose il seguente assioma:

Assioma di continuità di Dedekind
Per ogni sezione \((A, B)\) esiste un solo elemento \(\alpha \in \mathbb{R}\) tale che

\[ x \le \alpha \le y \ , \quad \forall x \in A, \forall y \in B \]

Il numero \(\alpha\) si chiama separatore della sezione \((A,B)\).
L’assioma di Dedekind permette di porre in corrispondenza biunivoca i punti della retta euclidea con gli elementi dell’insieme \(\mathbb{R}\). In altre parole la retta reale euclidea non presenta buchi, contrariamente alla retta costituita dai soli numeri razionali. Ricordiamo che Dedekind usava la parola continuità, mentre oggi è comune il termine completezza.
Sulle sezioni possiamo definire le \(4\) operazioni aritmetiche e stabilire le relazioni di ordinamento. In tal modo otteniamo degli oggetti che possiamo identificare con i numeri reali. Si può dimostrare che valgono le usuali proprietà commutativa, associativa e distributiva. In termini algebrici l’insieme dei numeri reali \(\mathbb{R}\), con le operazioni di addizione e moltiplicazione, è un campo totalmente ordinato. Dati due numeri reali \(a,b\), risulta verificata una ed una sola delle seguenti relazioni:

\[ a \lt b \ , \quad a = b \ , \quad a \gt b \]

1.1) Topologia degli insiemi di numeri reali

Un intervallo limitato aperto è un insieme \((a,b)=\{ x \in \mathbb{R}: a \lt x \lt b\}\). Un intervallo limitato chiuso è un insieme \([a,b]=\{x \in \mathbb{R}: a \le x \le b\}\). In modo simile si definiscono gli intervalli illimitati aperti \((-\infty,b), (a,+\infty)\) e gli intervalli illimitati chiusi \((-\infty,b], [a,+\infty)\).
Dal punto di vista geometrico gli intervalli limitati sono dei segmenti, mentre quelli illimitati sono delle semirette. La retta intera \((-\infty,+\infty)\) può essere considerata un intervallo illimitato sia superiormente che inferiormente.
Dato un punto \(x_{0} \in \mathbb{R}\), si chiama intorno di \(x_{0}\) un intervallo aperto \(I(x_{0})\) che contiene il punto. Un punto \(x_{0}\) si dice punto di accumulazione per un insieme \(A \subset \mathbb{R}\) se in ogni intorno \(I(x_{0})\) del punto \(x_{0}\) esiste almeno un elemento \(x\) diverso da \(x_{0}\) e appartenente all’insieme \(A\). In simboli

\[ \forall I(x_{0}) \quad \exists x \in A: x \in I(x_{0})\setminus \{x_{0}\} \]

Un punto di accumulazione può anche non appartenere all’insieme. Ad esempio, se \(A=\left\{1, \dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{3},\cdots\right\}\) allora il punto \(x=0\) è di accumulazione, ma non appartiene all’insieme \(A\). L’opposto di un punto di accumulazione è il punto isolato.

Definizione 1.2
Sia \(S \subset \mathbb{R}\). Un numero reale finito \(L\) si chiama maggiorante per l’insieme \(S\) se è maggiore od uguale ad ogni elemento di \(S\). Un numero reale finito \(l\) si chiama minorante se è minore od uguale ad ogni elemento di \(S\). Un insieme che ha un maggiorante si dice limitato superiormente, mentre un insieme che ha un minorante si dice limitato inferiormente. Un insieme si dice limitato se è limitato inferiormente e superiormente.
Un teorema fondamentale di analisi matematica è il seguente:

Teorema 1.1 – Bolzano-Weierstrass
Un insieme limitato contenente infiniti punti ammette almeno un punto di accumulazione.

Si chiama estremo superiore di \(S\) e si indica con \(\sup S\) il minimo dei suoi maggioranti. Si chiama estremo inferiore di \(S\) e si indica con \(\inf S \) il massimo dei suoi minoranti. Se appartengono all’insieme \(S\), l’estremo superiore e l’estremo inferiore coincidono rispettivamente con il massimo e il minimo dell’insieme stesso. Se l’insieme \(S\) non è limitato superiormente allora \(\sup S=+\infty\); se non è limitato inferiormente allora \(\inf S=-\infty\).
Dato un sottoinsieme \(S\) di \(\mathbb{R}\) definiamo l’insieme opposto \(-S =\{-x: x \in S\}\). Chiaramente abbiamo \(\inf (-S) = \sup S\).
L’assioma di continuità di Dedekind è equivalente al seguente assioma:

Assioma di completezza
Ogni sottoinsieme non vuoto \(S\) di numeri reali limitato superiormente ha un estremo superiore. Ogni sottoinsieme non vuoto \(S\) di numeri reali limitato inferiormente ha un estremo inferiore.

Esercizio 1.1
Dimostrare che le definizioni di \(l=\inf S\) e \(L=\sup S\) date in precedenza sono equivalenti alle seguenti proprietà:

\[ \begin{array}{l} \forall x \in S \quad \text{ risulta } l \le x \text{ e } x \le L \\ \forall \epsilon \gt 0 \quad \text{ esiste } x \in S \text{ tale che } x \lt l + \epsilon \\ \forall \epsilon \gt 0 \quad \text{ esiste } x \in S \text{ tale che } x \gt L – \epsilon \\ \end{array} \]

Esempio 1.3
Consideriamo il seguente insieme di numeri razionali:

\[ \begin{array}{l} S = \{x \in \mathbb{Q}: x^{2} \le 2\} \end{array} \]

Abbiamo \(\text{inf } S =- \sqrt{2}\) e \(\text{sup } S = \sqrt{2}\). Notiamo che gli estremi superiore ed inferiore esistono, ma non appartengono all’insieme dei numeri razionali. Quindi l’insieme non ha né massimo né minimo.

Esercizio 1.2
Trovare l’estremo inferiore e l’estremo superiore dell’insieme

\[ S=\{0,7; 0,77; 0,777; \cdots\} \]

Soluzione: \(\left[\text{inf S}=0,7; \text{sup S}=\dfrac{7}{9}\right]\)

Esercizio 1.3
Trovare l’estremo inferiore e l’estremo superiore dell’insieme

\[ S=\left\{\frac{1}{3}, \frac{4}{9}, \frac{13}{27}, \frac{40}{81}, \cdots\right\} \]

Suggerimento
Notare che il termine generale è \(\dfrac{1}{3^{n}}\sum\limits_{k=0}^{n-1}3^{k}\).

Soluzione: \(\left[\text{inf S}=\dfrac{1}{3}; \text{sup S}=\dfrac{1}{2}\right]\)

Esercizio 1.4
Dimostrare che l’insieme degli interi positivi \(Z^{+}=\{1,2,3,\cdots\}\) non è limitato superiormente.

Dimostrazione
Anche se l’affermazione appare ovvia, è comunque necessario dare una dimostrazione. Supponiamo per assurdo che l’insieme \(\mathbb{Z}^{+}\) sia limitato superiormente e poniamo \(\alpha = \sup \mathbb{Z}^{+}\). Allora per la proprietà dell’estremo superiore (vedi esercizio 1.1) deve esistere un intero positivo \(n\) compreso nell’intervallo \((\alpha -1, \alpha]\). Ma allora si avrebbe \(n+1 \gt \alpha\), contrariamente all’ipotesi iniziale.

Dall’esercizio precedente possiamo dedure la seguente fondamentale proprietà dei numeri reali:

Teorema 1.2 – Proprietà archimedea dei numeri reali
Se \(x,y \in \mathbb{R}\) e \(x \gt 0\), allora esiste un numero naturale \(n\) tale che \(nx \gt y\).

Un insieme di numeri reali \(A\) si dice denso in \(\mathbb{R}\) se fra due numeri reali qualsiasi esiste un numero dell’insieme \(A\).

Teorema 1.3
L’insieme dei numeri razionali \(\mathbb{Q}\) è denso in \(\mathbb{R}\).

Dimostrazione
Per la dimostrazione si può utilizzare la proprietà di Archimede. Consideriamo il caso di due numeri reali positivi \(x,y\) con \(x \lt y\). Per la proprietà di Archimede esiste un numero naturale \(q\) tale che \(q \gt \dfrac{1}{y-x}\). Inoltre l’insieme dei numeri naturali \(A=\{n \in \mathbb{N}| n \ge qy\}\) ha un elemento minimo \(p\). Poiché \(\dfrac{1}{q} \lt y\), deve essere \(p \gt 1\). Da questo deriva che il numero razionale \(r=\dfrac{p-1}{q}\) è compreso fra \(x\) e \(y\). Infatti abbiamo \(\dfrac{p-1}{q} \lt y\) e quindi

\[ \begin{array}{l} x= y-(y-x) \lt \dfrac{p}{q}-\dfrac{1}{q}=\dfrac{p-1}{q} \end{array} \]

Quindi nell’intervallo compreso fra due numeri reali qualsiasi esistono infiniti numeri razionali, così come esistono infiniti numeri irrazionali.

Esercizio 1.5
Dati due numeri reali \(a,b\) con \(a \lt b\), trovare l’espressione di un numero irrazionale \(\alpha\) compreso nell’intervallo \((a,b)\).

Soluzione: \(\left[\alpha = a+ \dfrac{1}{\sqrt{2}}(b-a)\right]\).

Esercizio 1.6
Calcolare l’estremo inferiore e superiore del seguente insieme:

\[ \left\{\sqrt{2},\sqrt{2+\sqrt{2}},\sqrt{2+\sqrt{}2+\sqrt{2}}, \cdots\right\} \]

Soluzione: \(\left[\sqrt{2};2\right]\)

Esercizio 1.7
Siano \(A,B\) due insiemi non vuoti di numeri reali positivi. Definiamo l’insieme prodotto

\[ A \cdot B=\{t=x \cdot y: x \in A, y \in B\} \]

Dimostrare che \(\sup (A \cdot B)= \sup A \cdot \sup B\).

Traccia
Per la dimostrazione utilizzare la proprietà dell’estremo superiore descritta nell’esercizio 1.1. Posto \(a = \sup A\) e \(b=\sup B\), per ipotesi fissato un \(\epsilon \gt 0\), esistono due numeri reali \(x_{\epsilon} \in A,y_{\epsilon} \in B\) tali che

\[ x_{\epsilon} \gt a -\epsilon \ , \quad y_{\epsilon} \gt b -\epsilon \]

Da questo deriva che \(x_{\epsilon}y_{\epsilon} \gt a \cdot b -\epsilon(a+b-\epsilon)\), concludendo la dimostrazione.
Con lo stesso metodo dimostrare che

\[ \sup \frac{1}{A}=\frac{1}{\inf A} \ , \quad \text{dove } \frac{1}{A}= \left\{t=\frac{1}{x}: x \in A\right\} \]

Esercizio 1.8
Siano \(A,B\) due insiemi non vuoti di numeri reali positivi. Definiamo

\[ \begin{array}{l} A + B = \{t = x + y: x\in A, y \in B\} \\ A – B = \{t = x – y: x\in A, y \in B\} \\ \end{array} \]

Dimostrare le seguenti formule:

\[ \begin{array}{l} \text{sup}(A+ B) = \text{sup A} + \text{sup B} \\ \text{sup}(A – B) = \text{sup A} – \text{inf B} \\ \text{inf}(A+ B) = \text{inf A} + \text{inf B} \\ \text{inf}(A – B) = \text{inf A} – \text{sup B} \\ \end{array} \]

Soluzione
Dimostriamo la prima relazione. Se uno degli insiemi \(A,B\) non è limitato superiormente allora la relazione è ovvia. Supponiamo quindi che \(\sup A\) e \(\sup B\) siano entrambi finiti. Dati \(x \in A, y \in B\) si ha \(x+y \le \sup A + \sup B\) e quindi \(\sup(A+B) \le \sup A + \sup B\).
Verifichiamo che vale anche la disuguaglianza opposta. Fissato un \(\epsilon \gt 0\), esistono \(x \gt \sup A – \dfrac{\epsilon}{2}\) e \(y \gt \sup B – \dfrac{ \epsilon}{2}\). Quindi

\[ x+y \gt \sup A + \sup B – \epsilon \quad \forall \epsilon \gt 0 \]

Da questo segue che \(\sup(A+B) \ge \sup A + \sup B\) e quindi mettendo insieme le due disuguaglianze abbiamo \(\sup(A+B)= \sup A + \sup B\).
Per dimostrare le altre relazioni ricordare che \(\sup(-A)=-\inf A\) e \(\inf(-A)=-\sup A\).

Esercizio 1.9
Calcolare l’estremo inferiore e superiore dei seguenti insiemi:

\[ \begin{array}{l} A= \{\sqrt{n}- \lfloor \sqrt{n} \rfloor: \quad n \in \mathbb{Z}^{+}\} \\ B= \left\{\dfrac{1}{n}- \dfrac{1}{m}:\quad n,m \in \mathbb{Z}^{+}\right\} \end{array} \]

Soluzione: \(\left[A=(0;1);B=(-1;1)\right]\)

Esercizio 1.10
Dimostrare le seguenti formule:

\[ \begin{array}{l} \sup (A \cup B) = \max (\sup A, \sup B) \\ \inf (A \cup B) = \min (\inf A, \inf B) \end{array} \]

dove \( A \cup B \) è l’unione dei due insiemi \(A,B\).

Esercizio 1.11
Calcolare gli estremi inferiori e superiori dei seguenti insiemi:

\[ \begin{array}{l} A = \left\{ \dfrac{2n+1}{n+1}: n \in \mathbb{Z^{+}}\right\} \\ B = \left\{ \dfrac{m}{n+m}: n,m \in \mathbb{Z^{+}}\right\} \\ C = \left\{ \dfrac{m}{n}+\dfrac{16n}{m}: n,m \in \mathbb{Z^{+}}\right\} \\ \end{array} \]

Soluzione: \( [ A=\left(\dfrac{3}{2}; 2\right)\); \(B= \left(0; 1\right)\); \(C=\left(8; +\infty\right) ]\).

Per un approfondimento dei numeri razionali e irrazionali vedere l’articolo su questo sito.

1.2) Disuguaglianze importanti

Ricordiamo alcune disuguaglianze utili nelle dimostrazioni dei teoremi. Teniamo a mente che il valore assoluto di un numero reale \(x\), indicato con \(|x|\), è così definito:

\[ |x|= \begin{cases} x \quad \text{se } x \ge 0 \\ -x \quad \text{se } x \lt 0 \\ \end{cases} \]

Teorema 1.4 – Disuguaglianza triangolare
Dati due numeri reali \(x,y\) si ha

\[ \begin{array}{l} |x+y| \le |x| + |y| \\ |x-y| \ge ||x| – |y|| \end{array} \]

Dimostrazione
Poiché \(-|x| \le x \le |x|\), abbiamo \(-(|x|+|y|) \le x+y \le (|x|+ |y|)\), da cui segue la prima parte del teorema.
Per la seconda parte osservare che \(|x|= |x-y+y| \le |x-y| + |y|\), da cui deriva facilmente il teorema.

Teorema 1.5 – Disuguaglianza di Bernoulli

\[ (1+x)^{n} \gt 1+nx \ , \quad n=2,3,\cdots; x \gt -1 \quad x \neq 0 \]

Dimostrazione
Il teorema è vero per \(n=2\) in quanto

\[ (1+x)^{2}=1+2x+x^{2} \gt 1+2x \]

Quindi procedere con il metodo di induzione.
Notiamo anche che \((1+x)^{n}=1+nx\) se e solo se \(n=1\) oppure \(x=0\).

Definizione 1.3
Dati \(n\) numeri reali positivi \(x_{1},x_{2},\cdots,x_{n}\), definiamo le seguenti medie:

\[ \begin{array}{l} A_{n}=\dfrac{x_{1}+ x_{2}+ \cdots +x_{n}}{n} \quad \quad \text{media aritmetica} \\ G_{n}=\sqrt[n]{x_{1}x_{2}\cdots x_{n}} \quad \quad \quad \quad \text{media geometrica}\\ H_{n}=\dfrac{n}{\dfrac{1}{x_{1}}+\dfrac{1}{x_{2}}+ \cdots +\dfrac{1}{x_{n}}} \quad \text{media armonica}\\ \end{array} \]

Teorema 1.6 – Disuguaglianza aritmetico-geometrica

\[ H_{n} \le G_{n} \le A_{n} \ , \quad n \ge 2 \]

La disuguaglianza \(G_{n} \le A_{n}\) viene chiamata disuguaglianza aritmetico-geometrica ed è indicata anche con il simbolo \(AM\text{-}GM\).

Dimostrazione
Presentiamo la dimostrazione data da Cauchy. Prima dimostriamo soltanto la \(G_{n}\le A_{n}\), nel caso \(n=2\). Abbiamo

\[ \left(\frac{x_{1}+x_{2}}{2}\right)^{2}=\left(\frac{x_{1}-x_{2}}{2}\right)^{2}+ x_{1}x_{2} \]

Quindi \(x_{1}x_{2}\le \left(\dfrac{x_{1}+x_{2}}{2}\right)^{2}\), da cui deriva la tesi.
Dimostriamo ora il teorema per \(n \gt 2\). Invece di provare con \(n=3\), seguendo Cauchy dimostriamo il teorema per \(n=4\). Per la relazione precedente abbiamo

\[ x_{1}x_{2}x_{3}x_{4}\le \left(\frac{x_{1}+x_{2}}{2}\right)^{2} \left(\frac{x_{3}+x_{4}}{2}\right)^{2} \]

Applicando la relazione iniziale ai numeri \(\dfrac{x_{1}+x_{2}}{2},\dfrac{x_{3}+x_{4}}{2}\), con semplici calcoli troviamo

\[ x_{1}x_{2}x_{3}x_{4}\le \left(\dfrac{x_{1}+x_{2}+x_{3}+x_{4}}{4}\right)^{4} \]

Proseguendo possiamo dimostrare il teorema per \(n=8,16, 32, \cdots\).
Resta da dimostrare il teorema per \(n=3,5,6,7, \cdots\). Osserviamo che, dati \(x_{1},x_{2},\cdots,x_{n}\) numeri positivi, possiamo trovare una potenza \(2^{k}\) tale che \(2^{k} \gt n\). Quindi definiamo i seguenti nuovi numeri:

\[ \begin{array}{l} y_{1}=x_{1}, y_{2}=x_{2}, \cdots, y_{n}=x_{n} \\ y_{n+1}=y_{n+2}= \cdots = y_{2^{k}}=A \end{array} \]

dove \(A= \dfrac{x_{1}+ \cdots + x_{n}}{n}\).
Possiamo applicare il teorema già dimostrato per il numero pari \(2^{k}\):

\[ x_{1}x_{2}\cdots x_{n}AA\cdots A \le \left(\frac{x_{1}+x_{2}+ \cdots + x_{n}+ A + A + \cdots + A}{2^{k}}\right)^{2^{k}} \]

Semplificando otteniamo il teorema.
La dimostrazione della disuguaglianza \(H_{n} \le G_{n}\) segue dalla \(G_{n} \le A_{n}\), utilizzando i numeri \(\dfrac{1}{x_{i}}\).

Esercizio 1.12 – Disuguaglianza Cauchy-Schwarz
Siano \(x_{1},x_{2}, \cdots ,x_{n}, y_{1},y_{2},\cdots, y_{n}\) dei numeri reali. Allora

\[ (x_{1}y_{1}+ \cdots + x_{n}y_{n})^{2}\le (x_{1}^{2}+\cdots + x_{n}^{2}) (y_{1}^{2}+\cdots + y_{n}^{2}) \]

Dimostrazione
Poniamo \(X=\sqrt{x_{1}^{2}+ \cdots + x_{n}^{2}}\) e \(Y=\sqrt{y_{1}^{2}+ \cdots + y_{n}^{2}}\). Per la disuguaglianza aritmetico-geometrica AM-GM abbiamo

\[ \sum\limits_{k=1}^{n}\frac{x_{k}y_{k}}{XY} \le \frac{1}{2}\sum\limits_{k=1}^{n}\left( \frac{x_{k}^{2}}{X^{2}} + \frac{y_{k}^{2}}{Y^{2}}\right) =1 \]

Quindi abbiamo

\[ \sum\limits_{k=1}^{n}\frac{x_{k}y_{k}}{XY} \le 1 \]

da cui segue la tesi.

Esercizio 1.13 – Disuguaglianza di Chebyshev
Siano dati due insiemi di numeri reali \(x_{1}\ge x_{2}\ge \cdots \ge x_{n}\) e \(y_{1}\ge y_{2}\ge \cdots \ge y_{n}\) (oppure \(x_{1}\le x_{2}\le \cdots \le x_{n}\) e \(y_{1}\le y_{2}\le \cdots \le y_{n}\)). Dimostrare con il metodo di induzione che

\[ \left( \sum\limits_{k=1}^{n}x_{k}\right) \left( \sum\limits_{k=1}^{n}y_{k}\right) \le n \sum\limits_{k=1}^{n}x_{k}y_{k} \]

Analizzare in quali casi si ha il segno di uguaglianza.

Esercizio 1.14 – Identità di Lagrange
Dimostrare che

\[ \left(\sum\limits_{k=1}^{n}x_{k}y_{k}\right)^{2}=\left(\sum\limits_{k=1}^{n}x_{k}^{2}\right)\left(\sum\limits_{k=1}^{n}y_{k}^{2}\right)- \sum\limits_{1 \le k \lt i \le n }\left(x_{k}y_{i}-x_{i}y_{k}\right)^{2} \]

Questa disuguaglianza implica anche la disuguaglianza di Cauchy-Schwarz.

Esercizio 1.15
Dimostrare la seguente disuguaglianza:

\[ \binom{n}{1} \binom{n}{2} \cdots \binom{n}{n-1} \le \left(\frac{2^{n}-2}{n-1}\right)^{n-1} \]

Suggerimento
Utilizzare la disuguaglianza AM-GM e ricordare che \(\sum\limits_{k=0}^{n}\binom{n}{k}=2^{n}\).

Per un approfondimento dei numeri reali vedere ^[1].

2) Successioni di numeri reali

Indichiamo con \(\mathbb{N}=\{0,1,2,\cdots\}\) l’insieme dei numeri naturali. Una successione è una funzione a valori reali il cui dominio è l’insieme dei numeri naturali \(\mathbb{N}\). La successione può essere rappresentata con \((x_{0},x_{1},x_{2},\cdots)\), oppure semplicemente indicando il termine generico \((x_{n})\). In altri casi può essere utile iniziare la successione con \(x_{1}\) oppure con \(x_{k}\) dove \(k\) può essere un intero qualunque, positivo o negativo.
In generale una successione può essere una sequenza arbitraria di numeri reali, senza alcuna relazione fra di essi. I casi più importanti sono quelli in cui si riesce a dare una formula esplicita per il termine \(n\)-esimo \(x_{n}\).

Esempio 2.1

\[ \begin{array}{l} x_{n}=\dfrac{1}{n^{2}}= \left (1,\dfrac{1}{4},\dfrac{1}{9},\cdots\right) \ , \quad n \gt 0\\ x_{n}=\sin \dfrac{n \pi}{2}= (1,0,-1,0,1,\cdots) \ , \quad n \gt 0 \\ \end{array} \]

Esercizio 2.1 – Numeri triangolari
Determinare l’espressione generica \(x_{n}\) della seguente successione: \(1,3,6,10,15,21,\cdots\).

Esercizio 2.2
Trovare il termine \(n\)-esimo della successione

\[ (x_{n})=(3,11,24,42,65,93,\cdots) \]

Soluzione:\(\left[ x_{n}=\dfrac{(5n+1)n}{2}\right]\)

2.1) Limite di una successione

Sia \((x_{n})\) una successione di numeri reali e sia \(L\) un numero reale. La successione \((x_{n})\) converge al numero \(L\) se per ogni numero reale \(\epsilon \gt 0\) esiste un numero naturale \(N\) tale che

\[ |x_{n}- L| \lt \epsilon \ , \quad n \ge N \]

Il numero \(L\) si chiama il limite della successione. Si usa la notazione \(L=\lim_{n \to \infty}x_{n}\) oppure \(x_{n} \to L\). Naturalmente il numero \(N\) in genere dipende dal valore di \(\epsilon\).
Diciamo che la successione \(x_{n}\) è divergente a \(+\infty\) se per ogni numero reale \(M\) esiste un numero naturale \(N\) tale che

\[ x_{n} \gt M \ , \quad n \ge N \]

In modo simile si definisce la divergenza a \(-\infty\).
Se la successione non converge ad un limite finito e non è divergente, allora si dice indeterminata oppure oscillante.
Il concetto di limite è alla base della definizione matematica della derivata e dell’integrale. Sostanzialmente la teoria dei limiti è basata sul fatto che tra due numeri reali ne esiste sempre un altro, quindi ne esistono infiniti. I matematici antichi, come Eudosso e Archimede, calcolavano le aree e i volumi mediante un processo simile di approssimazione, anche se non parlavano di limite. Leibniz e Newton fondarono il calcolo differenziale ed integrale con metodi geometrici, senza dare una definizione rigorosa del concetto di limite. Tuttavia nella sostanza le loro idee erano assai vicine alla definizione moderna. La definizione moderna di limite è stata fatta in particolare da Cauchy e Weierstrass nel secolo XIX. Il simbolo \(\lim \) è stato introdotto da Weierstrass.
Dalla definizione segue facilmente il seguente teorema di unicità:

Teorema 2.1 – Unicità del limite
Una successione \((x_{n})\) può convergere al massimo ad un solo numero reale. In altri termini se \(x_{n} \to a\) e \(x_{n} \to b\) allora \(a=b\).

Esercizio 2.3 – Regola di reciprocità
Sia \((x_{n})\) una successione di numeri reali. Dimostrare che

\[ \lim_{n \to \infty}x_{n} = \pm \infty \implies \lim_{n \to \infty}\dfrac{1}{x_{n}}=0 \]

Inoltre se \(x_{n} \gt 0\) allora

\[ \lim_{n \to \infty}\dfrac{1}{x_{n}}=0 \implies \lim_{n \to \infty}x_{n}=+\infty \]

Esercizio 2.4
Determinare un intero positivo \(N\), tale che per \(n \gt N\) è verificata la disuguaglianza \(x_{n} \gt 10^{9}\), per le seguenti successioni:

\[ \begin{array}{l} x_{n}=\sqrt{n} \\ x_{n}= n^{2} -10n + 5 \\ \end{array} \]

Esercizio 2.5
Determinare un intero positivo \(N\) e un numero reale \(L\), tali che per \(n \gt N\) è verificata la disuguaglianza \(|x_{n}-L| \lt 10^{-6}\):

\[ \begin{array}{l} x_{n}=\sqrt{10 + \dfrac{3}{n}} \\ x_{n}= \sqrt[n]{2} \end{array} \]

Il numero \(L\) non necessariamente deve essere il limite.

Esercizio 2.6
Determinare un intero positivo \(N\), tale che per \(n \gt N\) è verificata la disuguaglianza \(H_{n} \gt 10^{9}\):

\[ \begin{array}{l} H_{n}=1+ \dfrac{1}{2}+ \dfrac{1}{3}+ \cdots + \dfrac{1}{n} \end{array} \]

Suggerimento
Ricordare che \(H_{n} \gt \int\limits_{1}^{n+1}\dfrac{dx}{x}\).
I numeri \(H_{n}\) si chiamano numeri armonici.

Esercizio 2.7
Dimostrare che le seguenti successioni non sono convergenti.

\[ \begin{array}{l} x_{n}=\cos\left(n \dfrac{\pi}{2}\right) \\ x_{n}=n \left(1+(-1)^{n}\right) \\ x_{n}= \sin n \end{array} \]

Dimostriamo la terza relazione.
Supponiamo che \(\lim_{n \to \infty}\sin n =L\), con \(L \in \mathbb{R}\). Utilizziamo le formule trigonometriche di prostaferesi:

\[ \begin{array}{l} \sin \alpha -\sin \beta =2\left(\cos\dfrac{\alpha + \beta}{2}\right)\left(\sin\dfrac{\alpha -\beta}{2}\right) \\ \cos \alpha -\cos \beta =-2\left(\sin\dfrac{\alpha + \beta}{2}\right)\left(\sin\dfrac{\alpha -\beta}{2}\right) \\ \end{array} \]

Ponendo \(\alpha=n+2\) e \(\beta = n\) dalla prima formula abbiamo

\[ \lim_{n \to \infty}\sin (n+2) -\lim_{n \to \infty}\sin (n)=0=\lim_{n \to \infty}2 \cos(n+1)\sin(1) \]

Da questo deriva \(\lim_{n \to \infty}\cos n = 0\) e quindi per la seconda formula \(\lim_{n \to \infty} \sin n=0\). Ma questa è una contraddizione, in quanto per ogni \(n\) vale la formula \(\sin^{2}n + \cos^{2}n=1\).

Definizione 2.1
Una successione \((x_{n})\) si dice nulla se converge a zero. In altri termini se per ogni numero reale positivo \(\epsilon\) arbitrario è possibile trovare un numero intero positivo \(N \gt 0\) tale che

\[ |x_{n}| \lt \epsilon \ , \quad \text{ se } n \gt N \]

In termini intuitivi gli elementi di una successione nulla diventano arbitrariamente piccoli per valori di \(n\) sufficientemente grandi.

Esercizio 2.8
Dimostrare che la seguente successione è nulla

\[ \begin{array}{l} (x_{n})=(1,x,x^{2},x^{3}, \cdots) \ , \quad |x| \lt 1 \end{array} \]

Ovviamente una successione \((x_{n})\) converge ad un numero reale \(L\) se e solo se la successione \((x_{n}-L)\) è nulla.

Esempio 2.2
Supponiamo \(x_{n}=\dfrac{1}{n^{k}}\), con \(k \gt 0\). Allora \(x_{n} \to 0\) in quanto

\[ \frac{1}{n^{k}} \lt \epsilon \quad \text{se } n \gt e ^{-\dfrac{\ln \epsilon}{k}} \]

Esempio 2.3
Consideriamo la successione \(x_{n}=\dfrac{1}{\sqrt{n}}\). In questo caso è utile considerare un numero positivo \(\epsilon^{2}\). Poiché la successione \((y_{n})=\left(\dfrac{1}{n}\right)\) è nulla, esiste un indice \(N\) tale che \(\dfrac{1}{n} \lt \epsilon^{2}\) se \(n \ge N\). Quindi per \(n \ge N\) abbiamo

\[ |x_{n}-0|=\frac{1}{\sqrt{n}} \le \frac{1}{\sqrt{N}} \lt \sqrt{\epsilon^{2}}=\epsilon \]

Esercizio 2.9
Dimostrare che se \(x_{n} \to L\), \(x_{n} \gt 0\), allora

\[ \lim_{n \to \infty}\sqrt{x_{n}}=\sqrt{L} \]

Suggerimento
Se \(L=0\) l’affermazione è ovvia. Per il caso generale osservare che \(\sqrt{x_{n}}+ \sqrt{L} \ge \sqrt{L}\) ed effettuare la razionalizzazione.

Esercizio 2.10

\[ \lim_{n \to \infty} \dfrac{n}{b^{n}}= 0 \quad \text{ se } b \gt 1 \]

Sugggerimento
Posto \(b=1+t\), utilizzando il teorema binomiale di Newton abbiamo

\[ (1+t)^{n} \ge 1+ tn + \frac{n(n-1)}{2}t^{2} \]

Da questo concludere la dimostrazione.
Possiamo generalizzare l’esempio precedente mediante il metodo di induzione. Se \(k\) è un intero positivo dimostrare che

\[ \lim_{n \to \infty} \frac{n^{k}}{b^{n}}= 0 \quad \text{ se } b \gt 1 \]

Infine si può dimostrare che il limite vale anche nel caso \(k\) sia un numero reale.

Esercizio 2.11

\[ \lim_{n \to \infty} \frac{\ln n}{n^{\alpha}}=0 \ , \quad \alpha \gt 0 \]

Dimostrazione
Per ogni intero \(n \ge 2\) esiste un intero positivo \(k\) tale che \(e^{k} \le n \lt e^{k+1}\), quindi

\[ \frac {\ln n}{n^{\alpha}} \lt \frac{k+1}{e^{\alpha k}}= e^{\alpha} \frac{k+1}{(e^{\alpha})^{k+1}} \]

Per concludere la dimostrazione osservare che la successione \(y_{k}=e^{\alpha} \cdot \dfrac{k+1}{(e^{\alpha})^{k+1}}\) è una successione nulla.

Generalizzare il risultato precedente dimostrando che

\[ \lim_{n \to \infty} \frac{\ln^{\beta} n}{n^{\alpha}}=0 \ , \quad \alpha, \beta \gt 0 \]

2.2) Sottosuccessioni

Definizione 2.2
Sia \((x_{n})\) una successione. Supponiamo che la successione \(k \to n_{k}\) sia una successione crescente di numeri naturali. Allora diciamo che la \((x_{n_{k}})\) è una sottosuccessione di \((x_{n})\).
In altri termini l’elemento \(k\)-esimo della sottosuccessione è l’elemento \(n_{k}\)-esimo della successione iniziale \(x_{n}\).
Possiamo dare una definizione equivalente di punto di accumulazione: un numero \(x\) è un punto di accumulazione per la successione \((x_{n})\) se esiste una sottosuccessione \((y_{n})\) tale che \(\lim_{n \to \infty}y_{n}=x\).

Ad esempio la successione \(x_{n}=(-1)^{n}\) ha due punti di accumulazione, corrispondenti alle sottosuccessioni \((-1)^{2n}\) e \((-1)^{2n+1}\).
L’insieme dei punti di accumulazione può essere vuoto, finito oppure infinito.

Esercizio 2.12
Dare un esempio di successione con un numero finito fissato \(k \gt 2\) di punti di accumulazione.
Determinare anche una successione con un numero infinito di punti di accumulazione.

Teorema 2.2
Sia \((y_{n})\) una qualsiasi sottosuccessione di \((x_{n})\). Allora se la successione \((x_{n})\) converge, anche la \((y_{n})\) converge allo stesso limite.

Dimostrazione
Supponiamo che \(\lim_{n \to \infty}x_{n}=L\). Fissato un \(\epsilon \gt 0\), scegliamo un \(N\) tale che \(|x_{n}-L| \lt \epsilon\) se \(n \gt N\). Scegliamo ora un intero \(k_{0}\) tale che \(n_{k_{0}} \gt N\). Allora se \(k \ge k_{0}\) abbiamo \(n_{k} \ge n_{k_{0}} \gt N\) e quindi \(|y_{k}-L| = |x_{n_{k}}-L| \lt \epsilon\), che significa \(\lim_{n \to \infty}y_{n}=L\).

Dal teorema precedente deriva che le seguenti condizioni sono equivalenti:

\[ \begin{array}{l}
\lim_{n \to \infty}x_{n} = L \\
\lim_{n \to \infty}x_{n_{k}} = L \quad \text{per ogni sottosuccessione } (x_{n_{k}})\\
\end{array} \]

In modo equivalente, se una successione \((x_{n})\) non ha nessuna sottosuccessione convergente, allora \(|x_{n}| \to \infty\).

Esempio 2.4
Se una successione non è convergente, questo non implica che non esistano sottosuccessioni convergenti. Ad esempio la successione \(x_{n}=(-1)^{n}\) non è convergente. Tuttavia la sottosuccessione \(y_{n}=(-1)^{2n}\) è convergente a \(+1\).

2.3) Algebra dei limiti delle successioni

Il seguente teorema descrive le principali operazioni algebriche che possono essere effettuate con le successioni convergenti.

Teorema 2.3 – Algebra dei limiti
Siano \((x_{n}),(y_{n})\) due successioni di numeri reali tali che \(x_{n} \to A\) e \(y_{n} \to B\). Allora

\[ \begin{array}{l} \lim_{n \to \infty}(x_{n}\pm y_{n})= A \pm B \\ \lim_{n \to \infty}(x_{n}\cdot y_{n})= A \cdot B \\ \lim_{n \to \infty} \dfrac{x_{n}}{y_{n}}= \dfrac{A}{B} \quad \text{ se } B \neq 0 \\ \lim_{n \to \infty} x_{n}^{p}=A^{p} \\ \lim_{n \to \infty} p^{x_{n}}=p^{A} \\\end{array} \]

Le ultime due proprietà valgono per ogni numero reale \(p\) tale che \(A^{p}\) oppure \(p^{A}\) esista.

Dimostrazione
Dimostriamo solo la seconda proprietà. Le altre si dimostrano in modo analogo. Utilizzando la disuguaglianza triangolare abbiamo

\[ |x_{n}y_{n}-AB|=|x_{n}(y_{n}-B) +B(x_{n}-A)| \le |x_{n}||y_{n}-B| +|B||x_{n}-A| \]

Da questa disuguaglianza segue facilmente la tesi.

Esercizio 2.13
Determinare una successione di numeri irrazionali \(x_{n}\) tale che \(x_{n} \to 1\).

Esempio 2.5
Calcolare il limite della successione \(x_{n}=\dfrac{n^{3}+7n^{2}+5}{5n^{3}+3n-6}\).
In questo caso scriviamo l’espressione nella seguente forma:

\[ x_{n}=\dfrac{n^{3}\left(1+ \dfrac{7}{n}+ \dfrac{5}{n^{3}}\right)}{n^{3}\left(5+\dfrac{3}{n^{2}}-\dfrac{6}{n^{3}}\right) } \]

Da questo deriva che il limite è \(\dfrac{1}{5}\).

Esercizio 2.14
Dimostrare che se \(a \gt 0\) allora \(\lim_{n \to \infty}\sqrt[n]{a}=1\).

Soluzione
Se \(a=1\) allora è ovvio. Sia ora \(a \gt 1\). Posto \(x_{n}=\sqrt[n]{a}-1\), abbiamo \(a=(1+x_{n})^{n}\) con \(x_{n} \gt 0\). Per il teorema binomiale abbiamo \(nx_{n} \lt a\) e quindi \(x_{n} \lt \dfrac{a}{n}\), da cui deriva che \(x_{n} \to 0\).
Se \( 0 \lt a \lt 1\) poniamo \(b= \dfrac{1}{a}\). Poiché \(b \gt 1\) abbiamo \( \sqrt[n]{b} \to 1\) da cui deriva che \( \sqrt[n]{a} \to 1\).

Teorema 2.4 – Cauchy
Se \(x_{n} \to x\) allora

\[ \lim_{n \to \infty}\frac{S_{n}}{n}= \lim_{n \to \infty} \frac{x_{1}+x_{2}+ \cdots x_{n}}{n}=x \]

Dimostrazione
Supponiamo prima \(x=0\). Allora fissato un \(\epsilon \gt 0\) esiste un indice \(n_{0}\) tale che, per \(n \gt n_{0}\), risulta \(|x_{n}| \lt \dfrac{\epsilon}{2}\). Quindi

\[ \begin{array}{l} \dfrac{|S_{n}|}{n} \le \dfrac{x_{1}+ \cdots x_{n_{0}}}{n} + \dfrac{\epsilon}{2} \end{array} \]

Nella prima frazione il numeratore ha un valore fisso e quindi la frazione tende a zero al crescere di \(n\). Quindi esiste un indice \(n_{1}\) tale che la frazione è minore di \(\dfrac{\epsilon}{2}\). Quindi per \(n\) maggiore di \(\max(n_{0},n_{1})\) abbiamo \(\dfrac{|S_{n}|}{n}\lt \epsilon\).
Se \(\lim_{n \to \infty}x_{n}=x \neq 0\) allora basta applicare il ragionamento precedente alla successione \((x_{n}-x)\).

Lasciamo al lettore la dimostrazione del seguente:

Teorema 2.5 – Teorema del confronto (o dei due carabinieri)
Siano date tre successioni di numeri reali \(x_{n},y_{n},z_{n}\). Se \(x_{n} \le y_{n} \le z_{n}\) per ogni \(n\), allora

\[ \lim_{n \to \infty}x_{n}=\lim_{n \to \infty}z_{n}=L \quad \implies \lim_{n \to \infty}y_{n}=L \]

Esercizio 2.15
Calcolare il limite della seguente successione:

\[ x_{n}= \frac{5^{n}+(-3)^{n+1}}{5^{n-2}-3^{2n-1}} \]

In questo caso conviene trasformare in modo da avere lo stesso esponente \(n\) per tutte le potenze:

\[ x_{n}= \frac{5^{n}-3(-3)^{n}}{5^{n}5^{-2}-\left(\dfrac{1}{3}\right)9^{n}} \]

A questo punto mettiamo in evidenza i termini dominanti del numeratore \(5^{n}\) e del denominatore \(9^{n}\):

\[ x_{n}= \dfrac{5^{n}\left(1-3\dfrac{(-3)^{n}}{5^{n}}\right)}{9^{n}\left(5^{-2}\dfrac{5^{n}}{9^{n}}-\dfrac{1}{3}\right)} \]

Poiché \(\dfrac{5}{9} \lt 1\) è facile vedere che \(\lim_{n \to \infty}x_{n}=0\).

Esercizio 2.16
Dimostrare che

\[ \lim_{n \to \infty}\frac{n!}{n^{n}}=0 \]

Suggerimento
Scrivere

\[ \frac{n!}{n^{n}}= \frac{1}{n} \frac{2}{n} \cdots \frac{n-1}{n}\frac{n}{n} \]

Considerare separatamente il gruppo dei primi \(\left\lfloor \dfrac{n}{2}\right\rfloor\) e i restanti.

3) Successioni limitate e monotone

Una successione \((x_{n})\) si dice limitata se l’insieme dei suoi valori appartiene ad un insieme limitato di \(\mathbb{R}\). In altri termini, se esiste un numero reale positivo \(K\) tale che \(|x_{n}|\le K\) per ogni valore di \(n\). Il seguente teorema afferma che la limitatezza è una condizione necessaria per la convergenza.

Teorema 3.1
Sia \((x_{n})\) una successione convergente di numeri reali. Allora la successione è limitata.

Dimostrazione
Supponiamo che \(x_{n} \to L\). Allora, per un dato \(\epsilon \gt 0\), esiste un intero positivo \(N\) tale che \(|x_{n}-L| \lt \epsilon\) per \(n \gt N\). Quindi abbiamo \(|x_{n}| \lt K\) dove \(K=\max \{|x_{1}|, \cdots, |x_{N}|, |L| + \epsilon \}\).

In generale non è vero il viceversa. Una successione limitata non è necessariamente convergente. Ad esempio la successione \(x_{n}=(-1)^{n}\) è limitata ma non è convergente. Notiamo tuttavia che ha una sottosuccessione convergente. Ad esempio la successione \((1,1,1, \cdots)\).

Una successione \(x_{n}\) si dice crescente se risulta \(x_{n+1}\ge x_{n}, \forall n \in \mathbb{N}\). Si dice strettamente crescente se risulta \(x_{n+1}\gt x_{n}, \forall n \in \mathbb{N}\). Una successione \(x_{n}\) si dice decrescente se risulta \(x_{n+1}\le x_{n}, \forall n \in \mathbb{N}\). Si dice strettamente decrescente se risulta \(x_{n+1}\lt x_{n}, \forall n \in \mathbb{N}\). Una successione si dice monotona se è crescente oppure decrescente.
Una successione si dice eventualente crescente o decrescente se la proprietà vale da un certo indice \(N\) in poi.

Esempio 3.1
La successione \(\dfrac{10^{n}}{n!}\) è eventualmente decrescente.
Infatti si ha

\[ \frac{10^{n+1}}{(n+1)!} \le \frac{10^{n}}{n!} \iff 9 \le n \]

Esercizio 3.1
Dimostrare che le seguenti successioni sono monotone:

\[ \begin{array}{l} x_{n}= \ln n – n \ , \quad n \ge 1 \quad \text{ decrescente} \\ x_{n}= \dfrac{6n+1}{5n} \quad \text{crescente} \\ x_{n}= \dfrac{10^{n}}{n!} \quad \text{eventualmente crescente} \\ x_{n}= \arctan n \quad \text{crescente} \\ \end{array} \]

Teorema 3.2
Ogni successione monotona limitata di numeri reali è convergente. Precisamente, se la successione è limitata e crescente allora converge all’estremo superiore dell’insieme dei valori assunti. Se è limitata e decrescente converge all’estremo inferiore.

La dimostrazione segue facilmente dalle proprietà dell’estremo superiore e inferiore.

Possiamo quindi enunciare un criterio generale di convergenza per le successioni monotone:

Teorema 3.3
Una successione monotona di numeri reali \((x_{n})\) è convergente se e solo se è limitata. Se non è limitata ed è crescente allora tende a \(+\infty\). Se non è limitata ed è decrescente allora tende a \(-\infty\).

Un criterio utile per il calcolo del limite è il seguente:

Teorema 3.4 – Criterio del rapporto
Supponiamo che \(x_{n}\) sia una successione di numeri reali positivi tale che \(\lim_{n \to \infty}\dfrac{x_{n+1}}{x_{n}}=L\). Allora

\[ \begin{array}{l} \lim\limits_{n \to \infty}x_{n}=0 \quad \text{se } L \lt 1 \\ \lim\limits_{n \to \infty}x_{n}=\infty \quad \text{se } L \gt 1 \\ \end{array} \]

Dimostrazione
Dimostriamo il caso \(L \lt 1\). È evidente che se \(L \lt 1\) allora la successione è decrescente e limitata, e quindi è convergente. Per quanto riguarda il limite deve essere \(\lim_{n \to \infty }x_{n+1}=L\cdot \lim_{n \to \infty} x_{n}\), da cui segue \(\lim_{n \to \infty}x_{n}=0\).

Esercizio 3.2
Dimostrare che \(\lim_{n \to \infty}n^{k}x^{n}=0\), con \(|x| \lt 1\).

Esercizio 3.3 – Criterio della radice
Supponiamo che \(\lim_{n \to \infty}\sqrt[n]{|x_{n} |}=L\). Dimostrare che

\[ \begin{array}{l} \lim_{n \to \infty}x_{n}=0 \quad \text{se } L \lt 1 \\ \lim_{n \to \infty}|x_{n}|=\infty \quad \text{se } L \gt 1 \\ \end{array} \]

Un teorema fondamentale relativo alle successioni limitate è il seguente:

Teorema 3.5 – Bolzano-Weierstrass
Ogni successione limitata \((x_{n})\) di numeri reali ha un punto di accumulazione. In altri termini, ogni successione limitata ha almeno una sottosuccessione convergente.

Esercizio 3.4
Sia \((x_{n})\) una successione limitata di numeri reali, cioè esiste una costante positiva \(K\) tale che \(|x_{n}| \le K\) per tutti gli \(n\). Per ogni \(n\) definiamo l’insieme \(S_{n}=\{x_{n},x_{n+1}, x_{n+2},\cdots\}\) e la successione \((y_{n})= (\sup S_{n})=(\sup_{k \ge n}x_{k})\). Dimostrare che:

• la successione \((y_{n})\) è limitata superiormente e decrescente;
• la successione \((y_{n})\) converge ad un numero \(L\);
• il numero \(L\) è un punto di accumulazione per la successione \((x_{n})\). Quindi esiste una sottosuccessione di \((x_{n})\) che converge a \(L\).

3.1) Il numero di Eulero

Il numero di Eulero è la base dei logaritmi naturali. Il suo valore è definito come il limite della seguente successione:

\[ x_{n} =\left(1+\frac{1}{n}\right)^{n} \]

Vale il seguente teorema:

Teorema 3.6
La successione \((x_{n})\) è monotona crescente e limitata superiormente. Quindi esiste il limite finito, che viene indicato con la lettera e:

\[ e = \lim_{n \to \infty}\left(1+\frac{1}{n}\right)^{n} \approx 2,71828… \]

Dimostrazione
Dimostriamo prima che la successione è monotona crescente. Abbiamo

\[ \frac{x_{n+1}}{x_{n}}=\frac{n+1}{n}\left(1-\frac{1}{(n+1)^{2}}\right)^{n+1}\ge \frac{n+1}{n}\left(1-\frac{(n+1)}{(n+1)^{2}}\right)=1 \]

dove abbiamo utilizzato la disuguaglianza \((1+x)^{n} \ge (1+nx)\) per \(x \gt -1\).
Resta da dimostrare che la successione è limitata superiormente. Possiamo applicare il teorema binomiale. Poiché \(k! \ge 2^{k-1}\) abbiamo

\[ \begin{array}{l} \displaystyle x_{n}=\left(1+\dfrac{1}{n}\right)^{n}=\sum\limits_{k=0}^{n}\binom{n}{k}\dfrac{1}{n^{k}}= \\\sum\limits_{k=0}^{n}\dfrac{1}{k!}1 \cdot \left(1-\dfrac{1}{n}\right) \cdots \left(1-\dfrac{k-1}{n}\right) \\ \lt \sum\limits_{k=0}^{n}\dfrac{1}{k!} \le 1+\sum\limits_{k=0}^{n-1}\dfrac{1}{2^{k}} \end{array} \]

Ora, utilizzando la somma geometrica \(\sum\limits_{k=0}^{n-1}x^{k}=\dfrac{1-x^{n}}{1-x}\), possiamo concludere che

\[ \begin{array}{l} x_{n} \le 1+\sum\limits_{k=0}^{n-1}\dfrac{1}{2^{k}} =1 + 2\left(1- \dfrac{1}{2^{n}}\right) \lt 3 \end{array} \]

Il numero di Eulero è una delle costanti fondamentali della matematica. Si può dimostrare che si tratta di un numero irrazionale e trascendente (vedi articolo su questo sito).
Il numero di Eulero viene anche chiamato numero di Nepero, in onore del matematico John Napier (1500-1617) che utilizzò questo numero come base dei logaritmi.
Una definizione equivalente del numero di Eulero è quella di una base per la funzione esponenziale, che ha lo stesso valore della sua derivata. Cioè il numero di Eulero è l’unico numero tale che \(\dfrac{d}{dx}e^{x}= e^{x}\).

Esercizio 3.5

\[ \lim_{n \to \infty} \left(\dfrac{n+1}{n+3}\right)^{n}=\dfrac{1}{e^{2}} \]

Esercizio 3.6
Dimostrare che \(\lim\limits_{n \to \infty}\dfrac{\ln (1+x_{n})}{x_{n}}=1\) se \(x_{n} \gt 0\) e \(x_{n} \to 0\).

Esercizio 3.7
Calcolare il limite \(\lim_{n \to \infty}\dfrac{n!}{n^{n}}\).

Soluzione
Abbiamo già calcolato in precedenza questo limite. Calcoliamolo nuovamente sfruttando le proprietà delle successioni monotone e limitate. I primi valori sono

\[ x_{1}=1;\ x_{2}=\frac{1}{2};\ x_{3}=\frac{2}{9};\ x_{4}=\frac{3}{32} \]

La successione sembra essere monotona decrescente. Verifichiamolo in modo rigoroso:

\[ \frac{x_{n+1}}{x_{n}}=\frac{n^{n}}{(n+1)^{n}}=\left(\frac{n}{n+1}\right)^{n} \lt 1 \]

La successione è decrescente e limitata nell’intervallo \((0,1]\), quindi esiste il limite \(L\). In base alla formula precedente abbiamo

\[ L=\lim_{n \to \infty}x_{n}=\lim_{n \to \infty}x_{n+1} \cdot \lim_{n \to \infty}\left(1+\frac{1}{n}\right)^{n}= L\cdot e \]

Ma questo implica che deve essere \(L=0\).

Esercizio 3.8

\[ \begin{array}{l} \lim_{n \to \infty}\left(1+\dfrac{1}{n^{2}}\right)^{n}=1 \\ \lim_{n \to \infty}\left(1+\dfrac{1}{\sqrt{n}}\right)^{n}=\infty \\ \end{array} \]

Esercizio 3.9
Date le due successioni

\[ x_{n}=\left(1+\frac{1}{n}\right)^{n} \ , \quad y_{n}=\left(1+\frac{1}{n}\right)^{n+1} \]

Dimostrare che la successione \((x_{n})\) è crescente e la \((y_{n})\) è decrescente.

3.2) Limite inferiore e limite superiore

Sia \((x_{n})\) una successione limitata. Definiamo le seguenti successioni:

\[ \begin{array}{l} (S_{n})= \sup\{x_{n},x_{n+1},x_{n+2}, \cdots \} \\ (s_{n})= \inf\{x_{n},x_{n+1},x_{n+2}, \cdots \} \\ \end{array} \]

La successione \((S_{n})\) è monotona decrescente (o non crescente), mentre la \((s_{n})\) è monotona crescente (o non decrescente). Quindi entrambe sono convergenti.

Definizione 3.1
Il limite superiore della successione \((x_{n})\), indicato con \(\limsup x_{n}\), è

\[ \limsup_{n \to \infty} x_{n}= \lim_{n \to \infty} S_{n} \]

Il limite inferiore della successione \((x_{n})\), indicato con \(\liminf x_{n}\), è

\[ \liminf_{n \to \infty} x_{n}= \lim_{n \to \infty} s_{n} \]

Sono utilizzati anche i termini massimo limite e minimo limite.

Esempio 3.2
Data la successione \(x_{n}=(-1)^{n}\), si ha:

\[ \begin{array}{l} \liminf\limits_{n \to \infty} (-1)^{n}=-1 \\ \limsup\limits_{n \to \infty} (-1)^{n}=+1 \\ \end{array} \]

Esercizio 3.10
Dimostrare che

\[ \liminf_{n \to \infty} x_{n} \le \limsup_{n \to \infty} x_{n} \]

Vale il seguente teorema:

Teorema 3.7
Data una successione \((x_{n})\), si ha \(\lim_{n \to \infty}x_{n}=L\) se e solo se

\[ \limsup_{n \to \infty}x_{n}= \liminf_{n \to \infty}x_{n}=L \]

Esercizio 3.11
Supponiamo \(\limsup_{n \to \infty}x_{n}=L\) e \( \liminf_{n \to \infty}x_{n}=l\). Dimostrare che per ogni \(\epsilon \gt 0\) esiste un intero positivo \(N\) tale che \(x_{n} \lt L + \epsilon\), per tutti gli \(n \gt N\).
Inoltre per ogni \(\epsilon \gt 0\) esiste un intero positivo \(N\) tale che \(x_{n} \gt l-\epsilon\), per tutti gli \(n \gt N\).

Esercizio 3.12
Calcolare il massimo e minimo limite della successione

\[ x_{n}= (1+(-1)^{n})\sin \frac{n\pi}{4} \ , \quad n=1,2,\cdots \]

Soluzione: \([-2;2]\)

Esercizio 3.13
Determinare il limite inferiore e il limite superiore delle seguenti successioni:

\[ \begin{array}{l} x_{n}=\sin n\pi + \cos n \pi \\ x_{n}= \dfrac{n}{n+1}+ 2(-1)^{n}\\ x_{n}= (-1)^{n}+ (-1)^{n+2}\\ \end{array} \]

4) Numeri reali come limiti di successioni di razionali

Un numero razionale è un numero che può essere scritto nella forma \(\dfrac{a}{b}\), dove \(a,b\) sono interi e \(b \neq 0\). Nel sistema decimale ogni numero razionale \(x=\dfrac{a}{b}\) ha la seguente rappresentazione: 

\[ x = a_{0},a_{1}a_{2} \cdots a_{n}=a_{0}+ \frac{a_{1}}{10}+ \frac{a_{2}}{10^{2}}+ \cdots + \frac{a_{n}}{10^{n}} \]

Ad esempio \(\dfrac{21}{4}=5 + \dfrac{2}{10}+\dfrac{5}{100}=5,25\).

Alcuni numeri razionali hanno una espansione decimale infinita periodica. Ad esempio \(\dfrac{10}{3}=3,333\cdots\).
I numeri irrazionali hanno una rappresentazione con infinite cifre decimali, non periodica. Ad esempio \(\sqrt{2}=1,414213\cdots\).
Vale il seguente teorema:

Teorema 4.1
Dato un numero reale positivo \(y\), per ogni intero positivo \(n\) esiste un numero razionale con rappresentazione \(x_{n}=a_{0},a_{1}a_{2}\cdots a_{n}\) tale che

\[ x_{n}\le y \lt x_{n} + \frac{1}{10^{n}} \]

Dimostrazione
Poniamo \(a_{0}= \lfloor y \rfloor\), dove il simbolo \(\lfloor y \rfloor\) indica il più grande intero che è minore od uguale a \(y\). Chiaramente si ha \(a_{0} \le y \lt a_{0}+1\). Quindi definiamo

\[ a_{1}= \lfloor 10y -10a_{0}\rfloor \]

Risulta \(0 \le a_{1} \le 9\) e quindi

\[ a_{0}+ \frac{a_{1}}{10} \le y \lt a_{0}+ \frac{a_{1}+1}{10} \]

Proseguendo in modo analogo otteniamo

\[ a_{0}+ \frac{a_{1}}{10} + \cdots +\frac{a_{n}}{10^{n}} \le y \lt a_{0}+ \frac{a_{1}}{10} + \cdots + \frac{a_{n}+1}{10^{n}} \]

Quindi abbiamo

\[ x_{n} \le y \lt x_{n} + \frac{1}{10^{n}} \]

Un numero irrazionale può quindi essere definito come il limite di una successione di numeri razionali.

Teorema 4.2
Sia \(x\) un numero reale. Dimostrare che esiste una successione di numeri razionali \(x_{n}\) tali che \(x=\lim\limits_{n \to \infty}x_{n}\).

Suggerimento
Ricordare che fra due numeri irrazionali esiste sempre un numero razionale. Quindi per ogni \(n\) scegliere un numero razionale compreso nell’intervallo \(\left(x-\dfrac{1}{n},x\right)\).

Esempio 4.1
Il numero \(\sqrt{2}=1,4142 \cdots \) è irrazionale. Può essere definito come il limite della successione dei seguenti numeri razionali:

\[ x_{1}=1; \ x_{2}=1,4; \ x_{3}=1,41; \ x_{4}=1,414 \quad \cdots \]

Esempio 4.2
Il numero \(e\) di Eulero è un numero irrazionale. Può essere definito come il limite della seguente successione di numeri razionali:

\[ e = \lim_{n \to \infty} \left (1 + \dfrac{1}{1!}+ \dfrac{1}{2!}+ \cdots + \dfrac{1}{n!}\right) \]

5) Successioni di Cauchy

Definizione 5.1
Una successione \((x_{n})\) di numeri reale si chiama successione di Cauchy se per ogni \(\epsilon \gt 0\) esiste un intero positivo \(N\), dipendente in genere da \(\epsilon\), tale che

\[ |x_{n}-x_{m}| \lt \epsilon \ , \quad n,m \gt N \]

Ad esempio la successione \(x_{n}=\dfrac{1}{n}\) è una successione di Cauchy.
Possiamo confrontare queste due situazioni:

• In una successione convergente i termini diventano arbitrariamente vicini al limite.
• In una successione di Cauchy i termini diventano arbitrariamente vicini fra loro.

È facile verificare che una successione convergente è una successione di Cauchy. Infatti se \(x_{n} \to L\) allora abbiamo \(|x_{n}-L| \lt \epsilon\) per \(n \gt N\). Utilizzando la disuguaglianza triangolare abbiamo, per \(n,m \gt N\),

\[ |x_{n}-x_{m}|= |x_{n}-L-x_{m}+L| \le |x_{n}-L|+ |x_{m}-L| \le 2\epsilon \]

da cui segue la tesi.

Esempio 5.1
La successione \(x_{n}=\dfrac{2n+1}{5n}\) è una successione di Cauchy.
Abbiamo infatti \(|x_{n}-x_{m}|=\dfrac{n-m}{5nm}\). Prendendo \(N \gt \dfrac{1}{\epsilon}\) e \(n \gt m \gt N\) si ha

\[ |x_{n}-x_{m}|=\frac{n-m}{5nm} \le \frac{n}{mn}= \frac{1}{m} \le \frac{1}{N}\lt \epsilon \]

Esercizio 5.1
Dimostrare che le seguenti sono successioni di Cauchy:

\[ \begin{array}{l} x_{n}= 1- \dfrac{1}{2}+ \dfrac{1}{3}-\dfrac{1}{4}+ \cdots + \dfrac{(-1)^{n-1}}{n} \\ x_{n}= 1+ \dfrac{1}{1!}+ \dfrac{1}{2!}+ \cdots + \dfrac{1}{n!} \\ \end{array} \]

Dimostrazione
Per la prima successione, se \( m \gt n \gt N\) abbiamo

\[ |x_{m}-x_{n}|=\left|\frac{1}{n+1}-\frac{1}{n+2} + \cdots \pm \frac{1}{m}\right| \lt \frac{1}{n}\le \frac{1}{N} \]

Si può dimostrare che questa successione converge al valore \(\ln 2\).
Per la seconda successione ricordare la formula della somma geometrica \(\sum\limits_{k=0}^{n-1}x^{k}=\dfrac{1-x^{n}}{1-x}\).

Per essere una successione di Cauchy non è sufficiente che ogni termine sia arbitrariamente vicino al termine contiguo della successione.
Ad esempio consideriamo la successione dei numeri armonici \(H_{n}\):

\[ H_{n}=1+ \dfrac{1}{2}+ \cdots + \dfrac{1}{n} \]

In questo caso \(|H_{n}-H_{n+1}|=\dfrac{1}{n+1} \to 0\), tuttavia la successione \(H_{n}\) non è una successione di Cauchy e non converge.

Esercizio 5.2
Dimostrare che ogni successione di Cauchy è limitata.

Suggerimento
Basta osservare che esiste \( N\) tale che \( |x_{m}| \lt |x_{N}|+ 1\) per \( m \gt N\).

Possiamo enunciare il seguente criterio di convergenza:

Teorema 5.1 – Criterio di convergenza di Cauchy
Una successione di numeri reali è convergente se e solo se è una successione di Cauchy. Quindi ogni successione di Cauchy di numeri reali è convergente.

Traccia di dimostrazione
Osservare che, poiché è limitata, una successione di Cauchy \(x_{n}\) ha una sottosuccessione \(x_{n_{k}}\) convergente, con limite \(L\). Da questo dedurre, utilizzando la disuguaglianza triangolare, che prendendo \(N\) abbastanza grande si ha \(|x_{n}-L| \lt \epsilon\).

Il teorema precedente viene espresso dicendo che il campo dei numeri reali \(\mathbb{R}\) è completo.

Esercizio 5.3
Dimostrare con il criterio di Cauchy che la seguente successione \((s_{n})\) è convergente:

\[ s_{n}=1 + \frac{1}{2^{2}}+ \frac{1}{3^{2}}+ \cdots + \frac{1}{n^{2}} \]

Eulero nel 1735 dimostrò per primo che il limite della successione è \(\dfrac{\pi^{2}}{6}\) (vedi articolo su questo sito).

Esercizio 5.4
Dimostrare che se

\[ |x_{n+1}- x_{n}| \le \frac{1}{2^{n}} \ , \quad n \ge 0 \]

allora la successione è convergente.

Esercizio 5.5
Dimostrare con il criterio di Cauchy che la seguente successione \((s_{n})\) è convergente:

\[ s_{n}= \frac{\sin 1}{2}+ \frac{\sin 2}{2^{2}}+ \cdots +\frac{\sin n}{2^{n}} \]

Esercizio 5.6
Dimostrare che la successione

\[ \begin{array}{l} x_{1}=1 \\ x_{n+1}= \dfrac{x_{n}+2}{x_{n}+1} \ , \quad n \ge 1 \end{array} \]

é una successione di Cauchy. Quindi dimostrare che \(\lim_{n \to \infty}x_{n}=\sqrt{2}\).

5.1) Costruzione dei numeri reali secondo Cantor

Oltre alla definizione di Dedekind, i numeri reali possono essere definiti mediante le successioni di Cauchy. Sappiamo che per ogni numero reale esiste almeno una successione di numeri razionali che converge al numero stesso. Inoltre ogni successione di Cauchy converge ad un numero reale. Il metodo di Cantor consiste nell’associare ad ogni numero reale una classe di successioni di Cauchy di numeri razionali.
Indichiamo con \(C\) l’insieme di tutte le successioni di Cauchy di numeri razionali.

Definizione 5.2
Una successione di Cauchy \((x_{n})\) è equivalente a zero, oppure è una successione nulla, se \(\lim_{n \to \infty}x_{n}=0\).
Due successioni di Cauchy \((x_{n}),(y_{n})\) dell’insieme \(C\) si dicono equivalenti se la differenza \((x_{n}-y_{n})\) è una successione nulla.

Esercizio 5.7
Dimostrare che la relazione sopra descritta è una relazione di equivalenza, cioè riflessiva, simmetrica e transitiva.

Poiché è una relazione di equivalenza, l’insieme delle successioni di Cauchy di numeri razionali viene partizionato in una collezione di classi di equivalenza disgiunte. Ogni classe di equivalenza contiene tutte le successioni di Cauchy che sono equivalenti fra loro. Sull’insieme delle classi di equivalenza possono essere definite le operazioni di somma e moltiplicazione.
Vengono definite anche le usuali relazioni di ordinamento (maggiore, minore). Si può dimostrare che la struttura algebrica ottenuta è un campo algebrico ordinato.
Cantor definisce l’insieme dei numeri reali \(\mathbb{R}\) come l’insieme delle classi di equivalenza di successioni di Cauchy di numeri razionali. Il numero reale zero corrisponde alla classe di equivalenza contenente tutte le successioni nulle di \(C\).

Un campo di dice completo se ogni successione di Cauchy è convergente. Sappiamo che il campo dei numeri razionali \(\mathbb{Q}\) non è completo. Tuttavia vale il seguente teorema fondamentale:

Teorema 5.2
Il campo \(\mathbb{R}\) dei numeri reali di Cantor è completo.

Si può dimostrare che le definizioni di Dedekind e Cantor dei numeri reali sono equivalenti fra loro.

Esempio 5.2
Il numero \(\pi\) è rappresentato dalla successione di Cauchy

\[ \pi= \{3; \ 3,1; \ 3,14; 3,141; \ 3,1415; \ \cdots\} \]

Esempio 5.3
Il numero \(1\) è rappresentato da entrambe le seguenti successioni di Cauchy

\[ \begin{array}{l} x_{n}= \{1; \ 1,0; \ 1,00; \ 1,000; \ \cdots \cdots\} \\ y_{n}= \{0; \ 0,9; \ 0,99; \ 0,999; \ 0,9999; \ \cdots \cdots\} \\ \end{array} \]

6) Successioni ricorsive

Molte successioni importanti sono prodotte da una formula ricorsiva. Una definizione ricorsiva di una successione consiste di due parti: una relazione di ricorrenza ed una condizione iniziale. Una relazione di ricorrenza è una equazione che permette di calcolare il prossimo elemento della successione a partire dal precedente o dai precedenti.

Esercizio 6.1
Consideriamo la successione

\[ x_{n+1}= x_{n}^{2}+ \frac{1}{4} \ , \quad n=0,1,2,\cdots \]

Dimostrare che la successione converge se \(0 \le x_{0} \le \dfrac{1}{2}\) e diverge se \( x_{0} \gt \dfrac{1}{2}\).

Esercizio 6.2
Consideriamo la successione ricorsiva \((x_{n})\), tale che \(x_{1}=1\) e

\[ x_{n+1}=\frac{5(1+x_{n})}{5+x_{n}} \ , \quad n \ge 1 \]

Dimostrare che \(L=\lim_{n \to \infty}x_{n}= \sqrt{5}\).

Suggerimento
Dimostrare mediante il metodo di induzione che la successione è limitata; in particolare \(0 \le x_{n} \le \sqrt{5}\). Inoltre dimostrare che è non decrescente. Da questo deriva che il limite esiste finito. Naturalmente il limite \(L\) deve essere soluzione della seguente equazione

\[ L = \frac{5(1+L)}{5+L} \ , \quad n \ge 1 \]

Esercizio 6.3  
Sia data la successione

\[ x_{1}=1 \ , \quad x_{n+1}=\sqrt{x_{n}+2} \]

Dimostrare che la successione è monotona crescente e limitata. Quindi dedurre che \(x_{n} \to 2\).

6.1) I numeri di Fibonacci

I numeri di Fibonacci sono interi non negativi definiti dalla seguente equazione di ricorrenza:

\[ \begin{array}{l} F_{0} = 0 \\ F_{1} = 1 \\ F_{n} = F_{n-1} + F_{n-2} \ , \quad n \ge 2 \\ \end{array} \]

I primi numeri di Fibonacci sono \(\{0,1,1,2,3,5,8,13, \cdots \}\).

Soluzione dell’equazione di ricorrenza
Risolviamo l’equazione alle ricorrenze soddisfatta dai numeri di Fibonacci con il metodo della funzione caratteristica. Poniamo \(F_{k}= r^{k}\). In questo caso l’equazione caratteristica e le sue soluzioni sono le seguenti:

\[ \begin{array}{l} r^{2} – r – 1 = 0 \\ r_{1} = \dfrac{1 + \sqrt{5}}{2} \\ r_{2} = \dfrac{1 – \sqrt{5}}{2} \\ \end{array} \]

La soluzione generale dell’equazione omogenea è quindi

\[ F_{n} = A\left(\frac{1 + \sqrt{5}}{2}\right)^{n} + B \left(\frac{1 – \sqrt{5}}{2}\right)^{n} \]

Notiamo che la soluzione generale contiene due costanti arbitrarie. Tenendo conto delle condizioni iniziali \(F_{0}=0, F_{1}=1\), abbiamo infine la soluzione che dà la formula per i numeri di Fibonacci:

\[ F_{n} = \frac{1}{\sqrt{5}} \left(\frac{1 + \sqrt{5}}{2}\right)^{n} – \frac{1}{\sqrt{5}}\left(\frac{1 – \sqrt{5}}{2}\right)^{n} \]

Questa formula viene chiamata formula di Binet, in onore del matematico e astronomo francese Jacques Philippe Marie Binet (1786-1856).
La successione venne scoperta da Leonardo Pisano (1170-1235), chiamato anche Fibonacci. Questi numeri hanno importanti applicazioni in molti settori della matematica, della scienza e anche della vita reale. Per un approfondimento dei numeri di Fibonacci vedere ^[2].

Esercizio 6.4
Dimostrare le seguenti relazioni:

\[ \begin{array}{l} F_{1} + F_{3} + \cdots + F_{2n-1} = F_{2n} \\ F_{2} + F_{4} + \cdots + F_{2n} = F_{2n+1}-1 \\ \end{array} \]

Esercizio 6.5 – Numeri di Lucas
I numeri di Lucas (1842-1891) sono definiti con la stessa relazione di ricorrenza dei numeri di Fibonacci, ma cambiano le condizioni iniziali:

\[ \begin{array}{l} L_{0} = 2 \\ L_{1} = 1 \\ L_{n} = L_{n-1} + L_{n-2} \ , \quad n \gt 1 \\ \end{array} \]

I primi numeri di Lucas sono \(\{1,3,4,7,11,18, \cdots \}\). L’equazione di ricorrenza è la stessa dei numeri di Fibonacci, quindi la soluzione generale è la stessa. Tuttavia la soluzione particolare, ottenuta imponendo le due condizioni iniziali, è naturalmente diversa:

\[ L_{n} = \left(\frac{1 + \sqrt{5}}{2}\right)^{n} + \left(\frac{1 – \sqrt{5}}{2}\right)^{n} \]

Esercizio 6.6
Dimostrare la seguente relazione:

\[ F_{2n}=L_{n}F_{n} \]

Esercizio 6.7
Trovare una formula di ricorsione per la successione

\[ \dfrac{1}{1\cdot 2 \cdot 3}, \ \dfrac{1}{2\cdot 3 \cdot 4}, \ \dfrac{1}{3\cdot 4 \cdot 5}, \ \cdots \]

Esercizio 6.8
Sia \(t\) un numero reale positivo. Determinare il limite della seguente successione

\[ x_{n+1}= t + x_{n}^{2} \ , \quad n \ge 0; \ x_{0}=0 \]

Soluzione: \(\left[L=\dfrac{1 \pm \sqrt{1-4t}}{2}; \quad t \le \dfrac{1}{4}\right]\)

Esercizio 6.9
Calcolare il limite della seguente successione ricorsiva:

\[ \begin{array}{l} x_{1}= \sqrt{2} \\ x_{n+1}= \sqrt{2+ \sqrt{x_{n}}} \ , \quad n \ge 1 \end{array} \]

6.1) Metodi iterativi per risolvere equazioni

Un problema fondamentale in matematica è il calcolo degli zeri di una funzione \(f(x)\), dove la funzione può essere un polinomio o una funzione più generale. Tranne che nei casi più semplici, in generale non è possibile trovare delle formule esatte per calcolare gli zeri della funzione, cioè per risolvere l’equazione \(f(x)=0\). Per questo tipo di problemi può essere utile utilizzare dei metodi iterativi, che permettono di calcolare un valore approssimato delle radici, con la precisione desiderata. I metodi iterativi possono essere implementati facilmente mediante programmi eseguiti dai computer.

L’algoritmo di Erone
Il metodo di Erone di Alessandria (chiamato anche metodo babilonese) è un metodo iterativo che permette di calcolare il valore approssimato della radice quadrata di un numero reale positivo. Il metodo era già noto ai Babilonesi intorno al 1700 a.C.
Supponiamo di voler calcolare un valore approssimato della radice quadrata di un numero reale positivo \(\alpha\). L’algoritmo di Erone si applica per calcolare gli zeri della equazione

\[ x^{2}- \alpha = 0 \]

L’algoritmo inizia con un valore iniziale fissato \(x_{0}\) e calcola i valori successivi secondo la seguente formula iterativa:

\[ x_{n+1}= \frac{1}{2}\left(x_{n}+ \frac{a}{x_{n}}\right) \]

Si può dimostrare che \(\lim_{n \to \infty}x_{n}=\sqrt{\alpha}\). In termini intuitivi, se \(x_{n}\) è più grande della radice quadrata di \(\alpha\) allora il valore \(\dfrac{\alpha}{x_{n}}\) è più piccolo e la loro media aritmetica si avvicina al valore esatto di \(\sqrt{\alpha}\).

Esempio 6.1
Calcoliamo il valore approssimato della radice di \(2\).

Supponiamo di prendere \(x_{0}=1,5\). I primi passi dell’algoritmo sono i seguenti:

\[ \begin{array}{l} x_{1}=\dfrac{1}{2}\left(1,5 + \dfrac{2}{1,5}\right) \approx 1,41666667 \\ x_{2}=\dfrac{1}{2}\left(1,41666667+ \dfrac{2}{1,41666667}\right) \approx 1,41421569 \\ \end{array} \]

Il metodo di Erone è stato generalizzato da Newton. L’algoritmo di Newton (chiamato anche algoritmo di Newton-Raphson) permette di calcolare i valori approssimati delle radici di funzioni generali non lineari, non solo di semplici polinomi.
Per approfondire lo studio dei metodi iterativi utilizzati in analisi numerica vedere ad esempio ^[3] oppure ^[4].

7) Successioni di numeri complessi

I concetti esposti nei paragrafi precedenti si estendono in modo naturale ai numeri complessi. Per una introduzione ai numeri complessi vedere l’articolo su questo sito. Una successione di numeri complessi è una funzione che ad ogni numero naturale associa un numero complesso. La successione può essere indicata con \((z_{0},z_{1},z_{2},\cdots)\) o semplicemente indicando il termine generico \((z_{n})\). In altri casi può essere utile iniziare la successione con \(z_{1}\) oppure con \(z_{k}\) dove \(k\) può essere un intero qualunque, positivo o negativo.

Esempio 7.1
Esempi di successioni sono le seguenti

\[ \begin{array}{l} z_{n}= i^{n} \\ z_{n}=(1-i)^{n} \\ z_{n}=\left(1+\dfrac{i}{n}\right)^{n} \end{array} \]

Definizione 7.1
Una successione di numeri complessi \(z_{n}\) ha limite \(z\), se per ogni fissato numero reale \(\epsilon \gt 0\), esiste un intero positivo \(N\) tale che

\[ |z_{n}-z| \lt \epsilon \quad \text{ se } n \gt N \]

Ricordiamo che se \(z=x+iy\) allora il modulo del numero complesso è \(|z|=\sqrt{x^{2}+y^{2}}\).
Se il limite esiste la successione si dice convergente e si scrive \(\lim_{n \to \infty}z_{n}=z\). Se il limite non esiste la successione si dice divergente.
Ad esempio la successione \(z_{n}=i^{n}\) è divergente.
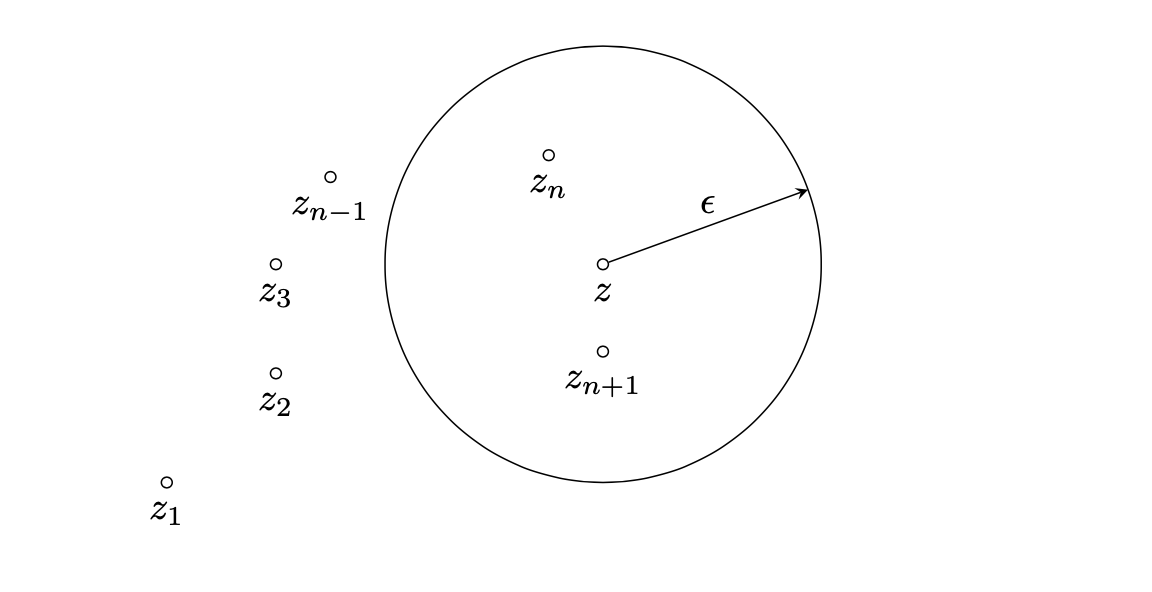
Dal punto di vista geometrico una successione di numeri complessi è un insieme di punti del piano complesso. Se la successione è convergente ad un punto \(z\) significa che, fissato un cerchio qualsiasi di raggio \(\epsilon\) con centro nel punto \(z\), tutti i termini della successione, tranne un numero finito, sono contenuti all’interno del cerchio.

Esercizio 7.1
Dimostrare che

\[ \begin{array}{l} \lim\limits_{n \to \infty} i^{4n}=1 \\ \lim\limits_{n \to \infty}\dfrac{i^{n}}{n}= 0 \\ \end{array} \]

Esercizio 7.2
Dimostrare che

\[ \begin{array}{l} \lim\limits_{n \to \infty} z^{n} = \begin{cases} 0 \quad \text { se } |z| \lt 1 \\ 1 \quad \text { se } z = 1 \\ \text{ divergente} \quad \text { se } |z| \gt 1 \end{cases} \end{array} \]

Il seguente teorema riduce lo studio delle successioni di numeri complessi allo studio di successioni di numeri reali.

Teorema 7.1
Sia \(z_{n}=x_{n}+iy_{n}\) una successione di numeri complessi che converge a \(z=x+iy\), dove \(x_{n},y_{n},x,y \in \mathbb{R}\). Allora

\[ \lim_{n \to \infty} z_{n}=z \iff \lim_{n \to \infty} x_{n}=x \text{ e }\lim_{n \to \infty} y_{n}=y \]

Per le successioni di numeri complessi valgono i teoremi sull’unicità del limite e sulle operazioni algebriche.

Si può estendere il teorema di Bolzano-Weierstrass:

Teorema 7.2
Ogni successione limitata di numeri complessi ammette almeno un punto di accumulazione.

Vale anche il criterio generale di convergenza di Cauchy: una successione di numeri complessi è convergente se e solo se è una successione di Cauchy.

Esercizio 7.3
Dimostrare usando la definizione di limite che

\[ \lim_{n \to \infty}\frac{1+in}{1+n}=i \]

Esercizio 7.4
Determinare i punti di accumulazione della successione \(x_{n}=\left(\dfrac{1+i}{1-i}\right)^{n}\).

Soluzione: \([1;-1;i;-i]\)

Esercizio 7.5
Verificare quale delle seguenti successioni convergono e, in caso affermativo, calcolare il limite:

\[ \begin{array}{l} x_{n}=\left(\dfrac{1}{1+i}\right)^{n} \\ x_{n}= \dfrac{n}{3n+1}+ i \dfrac{n-1}{n} \\ \end{array} \]

Soluzione: \([0; \frac{1}{3}+i]\).

Esempio 7.2 – L’insieme di Mandelbrot
L’insieme di Mandelbrot è l’oggetto frattale più famoso. È stato scoperto da B. Mandelbrot (1924-2010) nel 1979-1980, mentre studiava i punti del piano generati dalle successioni di numeri complessi del seguente tipo:

\[ z_{n+1}=z_{n}^{2}+ z_{0 } \]

dove \(z_{0}\) è un punto iniziale. La successione diverge o converge a seconda del punto iniziale scelto.
L’insieme di Mandelbrot consiste di tutti i valori complessi \(z_{0}\) per i quali la successione converge.

Esercizio 7.6
Dimostrare che nel caso \(z_{0}=1\) la successione diverge, mentre nel caso \(z=i\) la successione converge.

Per alcune immagini interessanti dell’insieme di Mandelbrot vedere il sito Wolfram.

8) Il teorema di Stolz-Cesaro

Un teorema molto utile per il calcolo del limite delle successioni di numeri reali è il seguente:

Teorema 8.1 – Stolz-Cesaro
Sia \((y_{n})\) una successione di numeri reali positivi tale che \(\lim_{n \to \infty}(y_{1}+ \cdots + y_{n})=\infty\). Allora se \((x_{n})\) è una successione qualsiasi si ha:

\[ \begin{array}{l} \limsup\limits_{n \to \infty}\left(\dfrac{x_{1}+x_{2}+ \cdots + x_{n}}{y_{1}+y_{2}+ \cdots + y_{n}}\right)\le \limsup\limits_{n \to \infty} \dfrac{x_{n}}{y_{n}} \\ \liminf\limits_{n \to \infty}\left(\dfrac{x_{1}+x_{2}+ \cdots + x_{n}}{y_{1}+y_{2}+ \cdots + y_{n}}\right)\ge \liminf\limits_{n \to \infty} \dfrac{x_{n}}{y_{n}} \\ \end{array} \]

In particolare se la successione \(\left(\dfrac{x_{n}}{y_{n}}\right)\) è convergente allora

\[ \lim_{n \to \infty}\frac{x_{1}+x_{2}+ \cdots + x_{n}}{y_{1}+y_{2}+ \cdots + y_{n}}= \lim_{n \to \infty} \frac{x_{n}}{y_{n}} \]

Dimostrazione
Per la dimostrazione utilizzare le proprietà dell’estremo superiore ed inferiore. Ad esempio, se \(L=\limsup_{n \to \infty}\dfrac{x_{n}}{y_{n}}\), allora per ogni \(t \gt L\) esiste un intero positivo \(k\) tale che

\[ \dfrac{x_{n}}{y_{n}} \le t \ , \quad n \gt k \]

Da questo deriva che per \( n \gt k\) si ha

\[ x_{1}+x_{2}+ \cdots + x_{n} \le x_{1}+x_{2}+ \cdots + x_{k} + t(y_{k+1}+y_{k+2}+ \cdots + y_{n}) \]

In modo simile simile si dimostra l’altra disuguaglianza.
Una formulazione equivalente del teorema precedente è la seguente:

Teorema 8.2
Sia \((y_{n})\) una successione di numeri reali positivi strettamente crescente tale che \(y_{n} \to \infty\). Allora se \((x_{n})\) è una successione qualsiasi si ha:

\[ \begin{array}{l} \limsup\limits_{n \to \infty}\dfrac{x_{n}}{y_{n}}\le \limsup\limits_{n \to \infty} \dfrac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}} \\ \liminf\limits_{n \to \infty}\dfrac{x_{n}}{y_{n}}\ge \liminf\limits_{n \to \infty} \dfrac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}} \\ \end{array} \]

In particolare se la successione \(\left(\dfrac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}}\right)\) è convergente allora

\[ \begin{array}{l} \lim\limits_{n \to \infty}\dfrac{x_{n}}{y_{n}}= \lim\limits_{n \to \infty} \dfrac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}} \end{array} \]

Dimostrazione
Basta considerare la successione \((a_{n})\), con \(a_{1}=x_{1}\) e \(a_{n}=x_{n}-x_{n-1}\) se \(n \ge 2\), e la successione \((b_{n})\), con \(b_{1}=y_{1}\) e \(b_{n}=y_{n}-y_{n-1}\) se \(n \ge 2\). Quindi applicare il teorema precedente alle due successioni \((a_{n})\),\((b_{n})\).

Esercizio 8.1
Dimostrare che se \(\lim_{n \to \infty}x_{n}=L\) allora

\[ \lim_{n \to \infty}\frac{x_{1}+x_{2}+ \cdots + x_{n}}{n}=L \]

La successione \(s_{n}=\dfrac{x_{1}+x_{2}+ \cdots + x_{n}}{n}\) si chiama media di Cesaro.

Definizione 8.1 – Convergenza secondo Cesaro
Una successione  \(x_{n}\) si dice convergente secondo Cesaro ad un numero finito \(L\) se esiste il limite

\[ \lim_{n \to \infty}\frac{x_{1}+x_{2}+ \cdots + x_{n}}{n}=L \]

Sappiamo che una successione convergente è anche convergente secondo Cesaro. Tuttavia non è vero il viceversa.
Ad esempio la successione \((1;0;1;0,1;0; \cdots)\) non è convergente, tuttavia converge a \(\dfrac{1}{2}\) secondo Cesaro.

Esercizio 8.2
Dimostrare che se \(\lim_{n \to \infty}x_{n}=L\), con \(x_{k} \gt 0\), allora

\[ \lim_{n \to \infty}\sqrt[n]{x_{1}x_{2}\cdots x_{n}}=L \]

Suggerimento
Ricordare che \(\sqrt[n]{x_{1}x_{2}\cdots x_{n}}=\exp \left({\dfrac{\ln x_{1}x_{2}\cdots x_{n}}{n}}\right)\), dove \(\exp(x)=e^{x}\).

Esercizio 8.3
Supponiamo \(\lim_{n \to \infty}x_{n}=x\) e \(\lim_{n \to \infty}y_{n}=y\). Dimostrare che

\[ \lim_{n \to \infty}\dfrac{x_{1}y_{n}+x_{2}y_{n-1}+ \cdots + x_{n}y_{1}}{n}=xy \]

Esercizio 8.4

\[ \lim_{n \to \infty}\dfrac{1+ \dfrac{1}{\sqrt{2}} + \cdots + \dfrac{1}{\sqrt{n}}}{\sqrt{n}}= 2 \]

8.1) Il teorema di Toeplitz-Silverman

Una estensione del teorema di Stolz-Cesaro è stata data da Otto Toeplitz (1881-1940).

Definizione 8.2 – Matrice di trasformazione regolare
Sia \(M=\{(c_{n,m}): n,m \in \mathbb{Z}^{+}, 1 \le m \le n\}\) una matrice di numeri reali. La matrice si dice matrice di trasformazione regolare se e solo se soddisfa le seguenti proprietà:

\[ \begin{array}{l} \lim\limits_{n \to \infty} c_{n,m} = 0 \\ \lim\limits_{n \to \infty} \sum\limits_{m=1}^{n} c_{n,m} = 1\\ \sum\limits_{m=1}^{n} \vert c_{n,m} \vert \lt K \end{array} \]

In altri termini ogni colonna converge a zero, le somme delle righe convergono a \(1\), le somme dei valori assoluti delle righe sono limitate.

Teorema 8.2 – Toeplitz-Silvermann
Sia \((c_{n,m})\) una matrice di trasformazione regolare. Allora, per ogni successione \((a_{n})\) convergente, la successione trasformata \((b_{n}=\sum\limits_{m=1}^{n}c_{n,m}a_{m})\) è convergente e si ha

\[ \lim_{n \to \infty}a_{n}=\lim_{n \to \infty}b_{n} \]

Per una dimostrazione vedere ^[5].

Esempio 8.1 – Matrice di Cesaro
La matrice di Cesaro \(C=(c_{ik})\)

\[ c_{mn}=\begin{cases}\frac{1}{m} & n\le m\\ 0 & n>m\end{cases} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & \cdots \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & \cdots \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 & 0 & \cdots \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 0 & \cdots \\ \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{pmatrix} \]

Si tratta di una matrice a trasformazione regolare. Se \(x_{n}\) è una successione convergente, la nuova successione \(y_{n}=\sum\limits_{k=1}^{n}c_{nm}x_{m}\) corrisponde alla media aritmetica:

\[ \lim_{n \to \infty}\frac{x_{1}+x_{2}+ \cdots + x_{n}}{n}=L \]

Come abbiamo visto nell’esercizo 8.1, se la \(x_{n} \to L\) allora anche \(y_{n} \to L\).

Esercizio 8.5
Dimostrare che il teorema di Toeplitz implica il teorema di Stolz-Cesaro.

Esercizio 8.6
Dimostrare che se \(\lim_{n \to \infty}x_{n}=+\infty\) allora

\[ \lim_{n \to \infty} \frac{x_{1}+x_{2}+ \cdots x_{n}}{n}=+\infty \]

Teorema 8.3  
Siano \((x_{n}), (y_{n})\) due successioni, tali che \(\lim_{n \to \infty}x_{n}=x, y_{n} \gt 0\) e \(\lim_{n \to \infty}\sum\limits_{k=1}^{n}y_{k}=+\infty\). Allora

\[ \lim_{n \to \infty} \frac{x_{1}y_{1}+x_{2}y_{2}+ \cdots x_{n}y_{n}}{y_{1}+y_{2}+ \cdots y_{n}}=x \]

Per un approfondimento dei metodi di sommazione vedere ^[5].

9) Metodi per il calcolo dei limiti delle successioni

Concludiamo l’articolo illustrando alcuni metodi e criteri utili per il calcolo dei limiti delle successioni. Ricordiamo le definizioni dei simboli di Landau, utili per studiare l’ordine di grandezza delle successioni e delle funzioni.

Definizione 9.1 – Simboli di Landau
Date due funzioni a valori reali \(f(x)\), \(g(x)\), definite su un dato dominio reale illimitato, e con \(g(x) \ge 0\), scriviamo

\[ f(x)= O(g(x)) \ , \quad x \to \infty \]

se esiste una costante reale positiva \(C\) e un numero reale positivo \(x_{0}\) tali che

\[ |f(x)| \le C g(x) \ , \quad x \ge x_{0} \]

Inoltre scriviamo

\[ f(x)= o(g(x)) \ , \quad x \to \infty \]

se risulta

\[ \lim_{x \to \infty} \frac{f(x)}{g(x)}=0 \]

Scriviamo poi \(f(x) \sim g(x)\) se risulta

\[ \lim_{x \to \infty} \frac{f(n)}{g(n)}=1 \]

I simboli \(O,o\) indicano collezioni di funzioni. Quindi la relazione \(f(x)=O(g(x))\) non va intesa come uguaglianza di funzioni, ma come inclusione.
I simboli di Landau sono stati definiti per le funzioni reali di variabile reale. Tuttavia si applicano anche per le successioni di numeri reali, che sono casi particolari di funzioni. Per le successioni le notazioni sono le seguenti:

\[ f(n)=O(g(n)), \ , f(n)=o(g(n)), \ , f(n) \sim g(n) \]

Se una successione \(f(n)\) è limitata allora \(f(n)=O(1)\).

Esempio 9.1

\[ \begin{array}{l} f(n) = \ln n + 10n^{2}+ 100 n^{3} \implies f(n)=O(n^{3}) \\ 1+2+ \cdots n =\dfrac{n(n+1)}{2}=O(n^{2}) \\ 1 + \dfrac{1}{2}+ \dfrac{1}{2}+ \cdots + \dfrac{1}{n} = O(\ln n) \\ 2^{n} +n^{4} \sim 2^{n} \\ \end{array} \]

Esercizio 9.1
Dimostrare che vale la seguente relazione

\[ \begin{array}{l} O(1) \subset O(\ln n) \subset O(n) \subset O(n\ln n) \subset O(n^{2}) \subset O(2^{n}) \subset O(n!) \subset O(n^{n}) \end{array} \]

9.1) Regola del termine dominante

Consideriamo la seguente successione:

\[ f(n)=\frac{5n^{3}+ 6n^{2}+10}{3n^{3}+4n} \]

In questo caso conviene dividere numeratore e denominatore della frazione per la massima potenza del denominatore:

\[ f(n)= \dfrac{5+ \dfrac{6}{n}+ \dfrac{10}{n^{3}}}{3 + \dfrac{4}{n^{2}}} \]

Abbiamo quindi \( f(n) \to \dfrac{5}{3}\).

Questo procedimento si chiama regola del termine dominante. Si può applicare a successioni il cui termine generale è un rapporto fra due polinomi nella variabile \(n\): \(f_{n}=\dfrac{p(n)}{q(n)}\). Se il grado di \(p(n)\) è \(r\) e il grado di \(q(n)\) è \(s\), allora possiamo distinguere tre casi:

\[ \begin{array}{l} r \lt s \implies \text{il limite è uguale a zero} \\ r \gt s \implies \text{il limite è } \pm\infty \\ r=s \implies \text{il limite è il rapporto dei coefficienti dei termini di grado massimo} \end{array} \]

Naturalmente la regola si applica anche nel caso le funzioni \(p(n),q(n)\) contengano altri termini diversi dalle potenze di \(n\), nel caso questi termini hanno un ordine di grandezza trascurabile, rispetto ai termini dominanti.

Esercizio 9.2
Dimostrare che

\[ \begin{array}{l} \lim\limits_{n \to \infty}\dfrac{10n^{3}+ (-1)^{n}+ \sin n^{2}}{2n^{3}+10}=5 \\ \lim\limits_{n \to \infty}\left(\dfrac{1}{n}- \dfrac{\ln (n+100)}{n^{2}}\right)=0 \end{array} \]

Esercizio 9.3

\[ \lim_{n \to \infty}\left(\sqrt{n^{2}+1}- \frac{n^{2}+1}{n+1}\right)=1 \]

Esercizio 9.4
Calcolare il seguente limite:

\[ \lim_{n \to \infty}\sqrt{\frac{\sqrt{n}- 4n^{3} + n \ln n}{3+n^{2} – n^{3}}} \]

Soluzione: [\(2\)]

9.2) Metodo di razionalizzazione

Il procedimento di razionalizzazione consiste nell’eliminare i simboli di radicali, oppure i numeri immaginari nel caso di numeri complessi, dal denominatore di una funzione razionale. Il metodo consiste nel moltiplicatore numeratore e denominatore per una espressione scelta in modo opportuno.

Esempio 9.2

\[ \begin{array}{l} \dfrac{5}{2+\sqrt{7}}=\dfrac{5(2-\sqrt{7})}{(2+\sqrt{7})(2-\sqrt{7})}= \dfrac{10 -5\sqrt{7}}{4-7} = \dfrac{-10 + 5\sqrt{7}}{3} \\ \dfrac{10}{2+3i}=\dfrac{10(2-3i)}{(2+3i)(2-3i)}= \dfrac{20 -30i}{4+9} =\dfrac{20-30i}{13} \\ \end{array} \]

Esercizio 9.5
Dimostrare che

\[ \lim_{n \to \infty} \frac{1}{n(\sqrt{n^{2}-1} -n)}=-2 \]

Esercizio 9.6

\[ \lim_{n \to \infty} \sqrt[4]{n^{4}+2n^{3}}- \sqrt[4]{n^{4}+n^{3}}= \frac{1}{4} \]

9.3) Funzioni continue

Ricordiamo la seguente proprietà delle funzioni continue:

Teorema 9.1
Sia \(f(x)\) una funzione reale di variabile reale continua, e sia \((x_{n})\) una successione di numeri reali. Se \(x_{n} \to x\) allora

\[ \lim_{n \to \infty}f(x_{n})= f(\lim_{n \to \infty}x_{n})=f(x) \]

Questa proprietà può essere utilizzata per calcolare il limite di successioni di numeri reali.

Esempio 9.3
Dimostrare che \(\lim\limits_{n \to \infty} \cos \left(\dfrac{n \pi}{2n+1}\right)=0\).
Poiché la funzione coseno è continua possiamo applicare il teorema:

\[ \lim_{n \to \infty} \cos \frac{n \pi}{2n+1}=0 = \cos\left(\lim_{n \to \infty} \frac{n \pi}{2n+1}\right) = \cos \frac{\pi}{2}=0 \]

Esercizio 9.7

\[ \lim_{n \to \infty} \ln \left(\frac{1+ 5n+ 10n^{2}}{15n^{2}+100}\right)= \ln \frac{2}{3} \]

Esercizio 9.8
Se \(x_{n}\) è una successione, con \(x_{n} \in (0,\infty)\), allora

\[ x_{n} \to a \implies \sqrt{x_{n}} \to \sqrt{a} \]

9.4) Forme indeterminate

Una forma indeterminata è una espressione che coinvolge due funzioni, e il limite non può essere determinato conoscendo il limite di entrambe le funzioni. Le principali forme indeterminate solo le seguenti:

\[ \frac{0}{0}; \ , \frac{\infty}{\infty}; \ , 0 \cdot \infty; \ , \infty – \infty; \ , 0 ^{0}; \ , \infty ^{0}; \ , 1 ^{\infty} \]

In questi casi è molto utile il seguente teorema:

Teorema 9.2 – de l’Hôpital (1661-1704)
Supponiamo di avere due funzioni \(f(x),g(x)\) derivabili tali che

\[ \lim_{x \to x_{0}}\frac{f(x)}{g(x)}= \frac{0}{0} \quad \text{oppure } \lim_{x \to x_{0}}\frac{f(x)}{g(x)}= \frac{\pm \infty}{\pm \infty} \]

dove \(x_{0}\) è un numero reale finito, oppure è uguale a \(\pm \infty\). Allora abbiamo

\[ \lim_{x \to x_{0}}\frac{f(x)}{g(x)}= \lim_{x \to x_{0}}\frac{f'(x)}{g'(x)} \]

Il teorema di Stolz-Cesàro può essere considerato la versione discreta del teorema di de l’Hôpital.  

Esempio 9.4
Calcoliamo il limite \(\lim_{n \to \infty}\sqrt[n]{n}\) con la regola di de l’Hôpital. Utilizziamo la funzione logaritmo, che è una funzione continua:

\[ \ln \lim_{n \to \infty} (\sqrt[n]{n})= \lim_{n \to \infty}\ln (\sqrt[n]{n})= \lim_{n \to \infty}\frac{\ln}{n}=0 \]

Da questo deriva che \(\lim_{n \to \infty}\sqrt[n]{n}=1\)

Esercizio 9.9
Sia \(x\) un numero reale. Dimostrare che

\[ \lim_{n \to \infty}\left(1+\frac{x}{n}\right)^{n}=e^{x} \]

Suggerimento
Considerare

\[ \ln \left(1+\frac{x}{n}\right)^{n} =n \ln \left(1+\frac{x}{n}\right)= \frac{\ln (1+\frac{x}{n})}{\frac{1}{n}} \]

e quindi applicare la regola di de l’Hôpital.

Esercizio 9.10
Calcolare il limite della successione \(\dfrac{n}{e^{n}}\).

Soluzione
Si tratta di una forma indeterminata \(\dfrac{\infty}{\infty}\). Possiamo applicare la regola di de l’Hôpital alla funzione \(\dfrac{x}{e^{x}}\). Quindi

\[ \lim_{n \to \infty}\frac{n}{e^{n}}=\lim_{x \to \infty}\frac{x}{e^{x}}= \lim_{x \to \infty}\frac{1}{e^{x}}=0 \]

Esercizio 9.11

\[ \lim_{n \to \infty}\frac{2^{n}}{n^{2}}=\infty \]

Esercizio 9.12
Calcolare nuovamente, con la formula di de l’Hôpital, il seguente limite:

\[ \lim_{n \to \infty} \frac{\ln x}{x^{\alpha}}=0 \ , \quad \alpha \gt 0 \]

9.5 ) Calcolo limiti con la serie di Taylor

Data una funzione \(f(x)\), la formula di Taylor permette di approssimare il valore della funzione nell’intorno di un suo punto \(a\) mediante una serie, i cui coefficienti sono ottenuti calcolando le derivate successive della funzione nel punto stesso. L’approssimazione è una serie del seguente tipo:

\[ \begin{array}{l} f\left( x \right) = \sum\limits_{n = 0}^\infty {\dfrac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{{\left( {x – a} \right)}^n}} \\ = f\left( a \right) + \dfrac{f^{(1)}\left( a \right)}{1!}\left( {x – a} \right) + \dfrac{{f^{(2)}\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \dfrac{{f^{(3)}\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} + \cdots \end{array} \]

Naturalmente per poter essere applicata devono esistere le derivate dei vari ordini nel punto in esame.
Ricordiamo gli sviluppi in serie di alcune funzioni, nell’intorno del punto \(x=0\):

\[ \begin{array}{l} e^{x} =1+x+ \dfrac{x^{2}}{2!}+ o(x^{2}) \\ \sin(x)= x-\dfrac{x^{3}}{3!}+ + o(x^{4}) \\ \cos(x) =1- \dfrac{x^{2}}{2!}+o(x^{3}) \\ \sinh(x)=\dfrac{e^{x}-e^{-x}}{2} = x+\dfrac{x^{3}}{3!}+o(x^{4}) \\ \cosh(x)=\dfrac{e^{x}+e^{-x}}{2} = 1+ \dfrac{x^{2}}{2!}+o (x^{3}) \\ (1+x)^{\alpha}= 1+ \alpha x + \dfrac{\alpha(\alpha -1)}{2}x^{2} + o(x^{2}) \ , \quad |x| \lt 1 \\ \ln(1+x)= x – \dfrac{x^{2}}{2} + o(x^{2}) \\ \end{array} \]

Esercizio 9.13
Calcolare il seguente limite con lo sviluppo di Taylor:

\[ \lim_{n \to \infty}n \ln \left(1-\frac{2}{n}\right)=-2 \]

Esercizio 9.14
Dimostrare nuovamente la formula

\[ \lim_{n \to \infty}\left(1+\frac{x}{n}\right)^{n}=e^{x} \]

Suggerimento
Utilizzare lo sviluppo del logaritmo, ricordando che \(\left(1+\dfrac{x}{n}\right)^{n}=\exp \left(n \ln \left(1+\dfrac{x}{n}\right)\right)\).

Esercizio 9.15

\[ \lim_{n \to \infty}n\left(e – \left(1+\dfrac{1}{n}\right)^{n}\right)=\dfrac{e}{2} \]

Esercizio 9.16

\[ \lim_{n \to \infty} \left(\frac{1}{n}+\frac{1}{n+1}+ \cdots + \frac{1}{2n}\right)= \ln 2 \]

9.6) Calcolo dei limiti mediante integrali

Alcuni limiti possono essere calcolati mediante l’utilizzo delle somme di Riemann e degli integrali di Riemann.
Supponiamo che \(f(x)\) sia una funzione continua in un intervallo \([a,b]\). Suddividiamo l’intervallo in \(n\) parti uguali di lunghezza \(\Delta x=\dfrac{b-a}{n}\). Allora l’integrale di Riemann può essere definito come il seguente limite:

\[ \int\limits_{a}^{b} f(x) dx=\lim_{n \to \infty} \frac{b-a}{n} \sum\limits_{k=1}^{n}f\left(a+k \frac{b-a}{n}\right) \]

Nal caso \(a=0,b=1\) abbiamo la seguente formula, utile per il calcolo di alcuni limiti:

\[ \int\limits_{0}^{1} f(x) dx=\lim_{n \to \infty} \frac{1}{n} \sum\limits_{k=1}^{n}f\left(\frac{k}{n}\right) \]

Esercizio 9.17
Sapendo che \(\int\limits_{0}^{1}x^{p}dx=\dfrac{1}{p+1}\), se \(p \gt -1\), dimostrare che

\[ \lim\limits_{n \to \infty} \dfrac{0^{p}+1^{p}+2^{p}+ \cdots + n^{p}}{n^{p}+ n^{p}+ n^{p}+ \cdots + n^{p}}=\dfrac{1}{p+1} \]

Esercizio 9.18

\[ \lim_{n \to \infty}\frac{1^{k}+2^{k}+ 3^{k}+ \cdots + n^{k}}{n^{k+1}}=\frac{1}{k+1} \]

Esercizio 9.19
Sia data la successione \(x_{n}=\dfrac{n}{1^{2}+n^{2}} +\dfrac{n}{2^{2}+n^{2}} + \cdots +\dfrac{n}{n^{2}+n^{2}}\). Dimostrare che

\[ \lim_{n \to \infty}x_{n}=\int_{0}^{1}\frac{1}{1+x^{2}}dx = \frac{\pi}{4} \]

Esercizio 9.20
Sia \(x\) un numero reale fissato. Dimostrare che

\[ \lim_{n \to \infty}\frac{1}{n}\left(\sin \frac{x}{n}+ \sin \frac{2x}{n}+ \cdots + \sin \frac{(n-1)x}{n}\right)= \frac{1-\cos x}{x} \ , \quad x \neq 0 \]

10) Alcuni esercizi proposti

Infine proponiamo ulteriori esercizi per coloro che vogliono migliorare le loro abilità nel calcolare i limiti delle successioni di numeri.

Esercizio 10.1

\[ \lim_{n \to \infty}\left(1-\frac{1}{2n+1}\right)^{3n}= \frac{1}{e \sqrt{e}} \]

Esercizio 10.2

\[ \lim_{n \to \infty} \left(\frac{1}{n}\right)^{n}+ \left(\frac{2}{n}\right)^{n}+ \cdots +\left(\frac{n}{n}\right)^{n}= \dfrac{e}{e-1} \]

Esercizio 10.3

\[ \lim_{n \to \infty}n \sin \frac{1}{n}=1 \]

Esercizio 10.4

\[ \lim_{n \to \infty}\frac{\sqrt[n]{2}-1}{\sqrt[n]{3}-1}=\frac{\ln 2}{\ln 3} \]

Suggerimento
Considerare la funzione \(f(x)=\dfrac{2^{x}-1}{3^{x}-1}\) e applicare la regola di de l’Hôpital.

Esercizio 10.5

\[ \lim_{n \to \infty}\left( \frac{1}{\sqrt{n(n+1)}}+ \frac{1}{\sqrt{(n+1)(n+2)}}+ \cdots + \frac{1}{\sqrt{2n(2n+1)}}\right)= \ln 2 \]

Esercizio 10.6

\[ \lim_{n \to \infty}\frac{1}{\sqrt{n}}\left(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+ \cdots +\frac{1}{\sqrt{n}}\right)= 2 \]

Esercizio 10.7

\[ \lim_{n \to \infty}\left(\frac{1}{\sqrt{1^{2}+n^{2}}}+ \frac{1}{\sqrt{2^{2}+n^{2}}}+ \cdots + \frac{1}{\sqrt{n^{2}+n^{2}}}\right)= \ln(1+ \sqrt{2}) \]

Esercizio 10.8

\[ \lim_{n \to \infty}\sqrt[n]{\frac{n^{n}}{n!}}= e \]

Utilizzare il teorema di Stolz-Cesaro.

Esercizio 10.9
Consideriamo la seguente progressione aritmetica: \(a, a+d, a+2d, \cdots, a+(n-1)d\), dove \(a,d\) sono numeri reali positivi. Dimostrare che

\[ \lim_{n \to \infty}\dfrac{G_{n}}{A_{n}}= \dfrac{2}{e} \]

dove \(A_{n}\) è la media aritmetica e \(G_{n}\) la media geometrica.

Esercizio 10.10

\[ \lim_{n \to \infty}\left(\frac{1+3+ 5 + \cdots + (2n-1)}{n+1} -\frac{2n+1}{2}\right)= \frac{-3}{2} \]

Esercizio 10.11

\[ \lim_{n \to \infty}\sqrt[n]{2^{n}-n}= 2 \]

Esercizio 10.12

\[ \lim_{n \to \infty}\left(\frac{\sin 1}{n^{2}+1}+ \frac{\sin 2}{n^{2}+2}+ \cdots + \frac{\sin n}{n^{2}+n}\right)=0 \]

Esercizio 10.13

\[ \lim_{n \to \infty}\frac{x_{n+1}}{x_{n}}=L \implies \lim_{n \to \infty}\sqrt[n]{x_{n}}=L \]

Utilizzare il teorema di Stolz-Cesaro.

Esercizio 10.14

\[ \lim_{n \to \infty} \left( 1+ \frac{1}{1!}+ \frac{1}{2!}+ \cdots + \frac{1}{n!}\right)= \lim_{n \to \infty}\left(1+ \frac{1}{n}\right)^{n}=e \]

Esercizio 10.15

\[ \lim_{n \to \infty} \frac{1}{n^{m+1}}\left( m!+ \frac{(m+1)!}{1!}+ \frac{(m+2)!}{2!}+\cdots + \frac{(m+n)!}{n!}\right)= \frac{1}{m+1} \ , \quad m \in \mathbb{N} \]

Utilizzare il teorema di Cesaro-Stolz.

Esercizio 10.16 – La costante di Eulero
Dimostrare che la seguente successione è convergente:

\[ \lim_{n \to \infty} 1+ \frac{1}{2}+ \frac{1}{3}+ \cdots + \frac{1}{n} – \ln n \]

Suggerimento
Dimostrare che la successione è monotona decrescente e limitata.
Il limite si chiama costante di Eulero e viene indicato con il simbolo \(\gamma\). Il valore approssimato è \(\gamma \approx = 0,5772156 \cdots\). Non è noto se si tratta di un numero razionale o irrazionale.

Conclusione

In questo articolo abbiamo introdotto il concetto fondamentale di limite, applicato alle successioni di numeri reali e complessi. In un prossimo articolo studieremo i metodi per determinare la convergenza e calcolare la somma delle serie infinite di numeri reali e complessi.

---

Bibliografia

^[1] Sergei Ovchinnikov – Real Analysis: Foundations (Springer)

^[2] Nikolai Nikolaevich Vorob’ev – Fibonacci Numbers (Dover Books on Mathematics)

^[3] S. D. Conte – Elementary Numerical Analysis: An Algorithmic Approach (SIAM-Society for Industrial and Applied Mathematics)

^[4] Alfio Quarteroni, Riccardo Sacco, Fausto Saleri, Paola Gervasio – Matematica numerica (Springer Verlag)

^[5] J. Boos – Classical and modern methods in summability (Oxford University Press)