In un precedente articolo di questo sito abbiamo visto che l’insieme dei numeri reali \(\mathbb{R}\) può essere decomposto in due sottoinsiemi disgiunti: i numeri razionali e i numeri irrazionali. In questo articolo vedremo una diversa suddivisione di \(\mathbb{R}\), altrettanto importante: i numeri algebrici e i numeri trascendenti.
1) I numeri algebrici e i numeri trascendenti
Definizione 1.1
Un numero \(\alpha\) reale o complesso si dice algebrico se è radice di un polinomio a coefficienti interi:
Se \(n\) è il grado minimo tra i polinomi che hanno \(\alpha\) come radice, allora si dice che \(\alpha\) è un numero algebrico di grado \(n\).
Una definizione equivalente è la seguente: un numero \(\alpha\) reale o complesso si dice algebrico se è radice di un polinomio monico, cioè con \(a_{0}=1\), a coefficienti razionali:
Un numero che non è algebrico si dice trascendente.
Chiaramente tutti i numeri interi e razionali sono algebrici, in quanto soddisfano l’equazione lineare di primo grado \(bx-a=0\).
Per quanto riguarda gli irrazionali vedremo in seguito che alcuni sono algebrici mentre altri sono trascendenti.
Esempio 1.1
I seguenti numeri sono algebrici:
L’esistenza dei numeri trascendenti non è facile da provare. Soltanto nel 1844 il matematico francese J. Liouville (1809-1882) dimostrò l’esistenza dei numeri trascendenti; in particolare, creò una classe intera di numeri trascendenti chiamati numeri di Liouville, che vedremo nei paragrafi successivi.
In seguito venne dimostrato che anche il numero \(\pi\) e la costante di Eulero \(e\) sono trascendenti. Mediante la teoria degli insiemi di Cantor venne poi dimostrato che l’insieme dei numeri trascendenti ha la potenza del continuo, come l’insieme dei numeri reali, mentre i numeri algebrici costituiscono un insieme numerabile.
2) Proprietà dei numeri algebrici
Teorema 2.1
L’insieme \(P\) di tutti i polinomi
è numerabile.
Dimostrazione
Indichiamo con \(P(m,n)\) l’insieme dei polinomi di grado \(n\) tali che
Per ogni coppia \(m,n\) l’insieme \(P(m,n)\) contiene un numero finito di elementi. Inoltre abbiamo
\[ P = \bigcup_{m,n} P(m,n) \quad m,n \in \mathbb{N} \]Quindi anche \(P\) è numerabile, in quanto per il teorema di Cantor l’unione numerabile di una famiglia di insiemi numerabile è numerabile.
Per il teorema di Cantor e la teoria degli insiemi vedere ad esempio il testo [1].
Teorema 2.2 – Cantor
L’insieme dei numeri algebrici è numerabile.
Dimostrazione
Per il teorema precedente l’insieme di tutti i polinomi a coefficienti interi è numerabile, e quindi possiamo etichettare ogni polinomio con un indice intero positivo, cioè:
Per ogni equazione \(p_{i}(x)=0\) indichiamo con \(A_{i}\) l’insieme dei numeri algebrici soluzioni del polinomio:
\[ A_{i} = \{x| p_{i}(x)=0 \} \]Gli insiemi \(A_{i}\) sono finiti, in quanto per il teorema fondamentale dell’algebra ogni polinomio di grado \(n\) può avere al massimo \(n\) soluzioni. L’insieme dei numeri algebrici \(A\) è l’unione di una famiglia numerabile di insiemi finiti \(A_{i}\) e quindi è numerabile.
Come è noto Cantor ha anche dimostrato che l’insieme dei numeric reali \(\mathbb{R}\) non è numerabile, ma ha la potenza del continuo. Dal teorema precedente deriva quindi che la maggior parte dei numeri reali è trascendente.
Teorema 2.3
L’insieme dei numeri algebrici forma un campo: cioè la somma, il prodotto e il quoziente di due numeri algebrici sono anch’essi numeri algebrici.
Per una dimostrazione vedere [2].
3) Il teorema di Liouville
La dimostrazione di Cantor dimostra soltanto l’esistenza dei numeri trascendenti, ma non fornisce un esempio concreto. Il primo esempio concreto di numero trascendente venne fornito nel 1844 da Liouville.
In primo luogo osserviamo che se \(\alpha\) è un numero algebrico, allora esiste un unico polinomio irriducibile \(p(x)\) a coefficienti interi con queste proprietà:
- \(p(\alpha)=0\)
- il coefficiente principale \(a_{0}\) è positivo
- i coefficienti \(a_{i}\) sono primi fra loro
Il polinomio \(p(x)\) viene chiamato polinomio minimale.
Teorema 3.1 – Liouville
Sia \(\alpha \) un numero algebrico irrazionale di grado \(d\). Allora esiste una costante positiva \(k(\alpha)\), dipendente solo da \(\alpha\), tale che per ogni numero razionale \(\dfrac{p}{q}\) si ha:
Dimostrazione
Il teorema vale anche nel caso di numeri complessi. Tuttavia, in questa sede supponiamo che \(\alpha \) sia un numero reale.
Possiamo supporre \( k \lt 1\), in quanto se il teorema è vero per un dato valore \(k\), allora è vero anche per un valore positivo più piccolo. La disuguaglianza vale sicuramente per le frazioni \(\dfrac{p}{q}\) tali che \(\left|\alpha -\dfrac{p}{q}\right| \gt 1\). Per questo possiamo supporre \(\left|\alpha -\dfrac{p}{q}\right| \le 1\), quindi la frazione \(\dfrac{p}{q}\) è limitata.
Sia \(f(x)\) il polinomio minimale per \(\alpha\):
Il polinomio è irriducibile, i coefficienti sono primi fra loro e \(f(\alpha)=0\). Chiaramente \(f\left(\dfrac{p}{q}\right)\neq 0\) per tutti i numeri razionali \( \dfrac{p}{q} \in \mathbb{Q}\), in quanto il grado di \(\alpha\) è \(\gt 1\) e il polinomio è irriducibile. Quindi
\[ \left|q^{d}f\left(\frac{p}{q}\right)\right|=\left|a_{0}p^{d}+a_{1}p^{d-1}q + \cdots + a_{d}q^{d}\right| \ge 1 \]Applicando il teorema della media alla funzione \(f(x)\), abbiamo
\[ f\left(\frac{p}{q}\right) = f\left(\frac{p}{q}\right)- f(\alpha)= \left(\frac{p}{q}- \alpha\right) f'(\theta)\\ \]dove il punto \(\theta\) è compreso nell’intervallo fra \(\alpha\) e \(\dfrac{p}{q}\). Poiché abbiamo supposto \(\left|\alpha -\dfrac{p}{q}\right| \le 1\), abbiamo \(\alpha -1 \le \theta \le \alpha +1\) e quindi
\[ |f'(\theta)| \le \text{max} \{|f'(x)|: x \in [\alpha-1,\alpha+1]\} \]Poiché \(f'(x)\) è una funzione continua nell’intervallo, per il teorema di Weierstrass il valore \(f'(\theta)\) è limitato da una costante \(h \gt 1\). Possiamo quindi scrivere
\[ \left|\frac{p}{q}- \alpha\right|= \frac{\left| q^{d}f\left(\dfrac{p}{q}\right)\right|}{q^{d}\left|f'(\theta)\right |} \ge \frac{1}{hq^{d}}\\ \]Il teorema di Liouville è quindi dimostrato ponendo \(k=\dfrac{1}{h}\).
Il teorema di Liouville ha una importanza fondamentale nello studio dei numeri algebrici. Il teorema è stato generalizzato da Roth (1925-2015), il quale è riuscito ad ottenere l’esponente migliore per l’approssimazione di numeri algebrici irrazionali tramite numeri razionali.
Teorema 3.2 – Roth
Sia \(\alpha\) un numero algebrico di grado \(d \ge 2\) e sia \(\epsilon \gt 0\) un numero reale positivo arbitrario. Allora esiste una costante \(k(\alpha,\epsilon) \gt 0\) tale che per tutti i numeri razionali \(\dfrac{p}{q}\) ,
Per una dimostrazione del teorema vedere [3] oppure [6].
Mediante il teorema di Roth è possibile dimostrare che il seguente numero
è un numero trascendente. Questo numero viene chiamato costante di Champernowne, o anche numero di Mahler, in onore del matematico tedesco Kurt Mahler (1903-1988), che ha dato importanti contributi alla teoria dei numeri trascendenti. Per una panoramica delle interessanti proprietà di questo numero vedere Wikipedia.
Il teorema di Roth fornisce l’approssimazione migliore possibile. Infatti vale il seguente teorema:
Teorema 3.3 – Dirichlet
Dato un numero irrazionale \(\alpha\) si ha:
per infiniti valori di \(p,q\).
4) I numeri di Liouville
Il teorema di Liouville può essere formulato anche in questa versione equivalente:
Teorema 4.1 – Liouville
Sia \(\alpha \) un numero reale. Supponiamo che per ogni costante positiva \(\epsilon\) e ogni intero positivo \(d\) esiste un numero razionale \(\dfrac{p}{q}\) tale che
Allora il numero \(\alpha\) è trascendente.
Utilizzando quest seconda versione possiamo introdurre una classe di numeri che sono tutti trascendenti.
Definizione 4.1 – I numeri di Liouville
I numeri di Liouville sono i numeri irrazionali \(\alpha\) tali che, per ogni intero positivo \(d\), esiste un numero razionale \(\dfrac{p}{q}\), con \(q \gt 1\), tale che
Vediamo ora un esempio di numero irrazionale fornito da Liouville.
Teorema 4.2 – La costante di Liouville
Il numero
è trascendente. Le cifre assumono il valore \(1\) nelle posizioni decimali corrispondenti a \(n!\): \(1,2,6,24, \cdots\).
Dimostrazione
Fissiamo un intero positivo arbitrario \(N\). Dato un intero positivo \(n\gt N\), poniamo \(S_{n}=\sum\limits_{k=1}^{n}\dfrac{1}{10^{k!}}\). Si tratta di un numero razionale e quindi possiamo scrivere
Abbiamo
\[ 0 \lt L -S_{n}=10^{-(n+1)!} + 10^{-(n+2)!} + \cdots \lt 2 \cdot 10^{-(n+1)!} \lt 2q^{-N} \]Poiché \(N\) è un intero arbitrario, dal teorema 4.1 deriva che \(L\) deve essere trascendente.
Per la stima precedente abbiamo fatto uso della proprietà della serie geometrica:
\[ \sum\limits_{k=n+1}^{\infty}10^{-k!} \lt \sum\limits_{k=(n+1)!}^{\infty}10^{-k} =\frac{10}{9}10^{-(n+1)!} \]
La proprietà caratteristica della costante di Liouville è la grande velocità di approssimazione mediante numeri razionali.
In modo analogo si può dimostrare il seguente:
Teorema 4.3
Tutti i numeri della forma
dove \(a_{k} \in \{1,2,3, \cdots, 9\}\) sono trascendenti.
Un teorema interessante, dimostrato dal matematico ungherese Erdos, è il seguente:
Teorema 4.4 – Erdos
Ogni numero reale si può esprimere come somma di due numeri di Liouville.
Per una dimostrazione vedere [5].
5) La costante di Eulero-Nepero
La costante di Eulero-Nepero, indicata con il simbolo \(e\), può essere definita mediante il seguente limite:
\[ e = \lim_{n \to \infty}\left(1+\dfrac{1}{n}\right)^{n} \approx 2,7182 \]L’irrazionalità della costante di Eulero-Nepero \(e\) venne dimostrata da Eulero nel \(1737\), mentre la sua trascendenza venne dimostrata da C. Hermite (1822-1901) nel \(1873\).
Per la dimostrazione della trascendenza è utile definire la seguente funzione \(h(x)\):
dove \(p\) è un numero primo. Si tratta di un polinomio di grado \(np+p-1\), da cui segue che la derivata \(h^{(np+p)}(x)=0\).
Notiamo che possiamo scrivere la funzione nella forma seguente:
dove i coefficienti \(c_{k}\) sono interi.
Esercizio 5.1
Dimostrare che
Esercizio 5.2
Dimostrare che
Se invece \( j \neq 0\) e \(k \in \{0,1,\cdots, np+p-1\}\), si ha \(h^{(k)}(j) \equiv 0 \pmod{p}\).
Teorema 5.1 – Hermite
La costante \(e\) di Eulero è un numero trascendente.
Dimostrazione
Supponiamo che \(e\) sia algebrico e quindi
dove i coefficienti \(a_{i}\) sono interi e \(a_{0} \neq 0\). Definiamo la funzione
\[ H(x)= h(x) + h^{(1)}(x) + \cdots + h^{np+p-1}(x) \]È facile verificare che \(H(x) -H^{(1)}(x)=h(x)\) e quindi abbiamo
\[ \frac{d}{dx}(e^{-x}H(x))= -e^{-x} h(x) \]Applicando il teorema fondamentale del calcolo integrale abbiamo
\[ a_{k}\int\limits_{0}^{k}e^{-x}h(x)dx = a_{k}H(0) -a_{k}e^{-k}H(k) \]La relazione precedente è vera per ogni \(k\). Moltiplicando entrambi i lati dell’equazione per \(e^{k}\) e sommando, abbiamo
\[ \sum\limits_{k=0}^{n}\left(a_{k}e^{k}\int\limits_{0}^{k}e^{-x}h(x)dx\right) = -\sum\limits_{k=0}^{n}\sum\limits_{i=0}^{np+p-1}a_{k}h^{(i)}(k) \]Ora in base all’esercizio 5.2, se scegliamo \(p \gt n\) e \(p \gt |a_{0}|\) allora ogni termine nella doppia somma è un multiplo di \(p\), ad eccezione del termine \(-a_{0}h^{(p-1)}(0)\). Quindi il membro di destra dell’equazione precedente rappresenta un intero non divisibile per \(p\) e quindi non nullo. A questo punto per completare la dimostrazione del teorema basta dimostrare che il membro di sinistra in realtà tende a zero, al tendere di \(p\) all’infinito. Infatti abbiamo
\[ \left|\sum\limits_{k=0}^{n}a_{k}e^{k}\int\limits_{0}^{k}e^{-x}h(x)dx \right| \le \sum\limits_{k=0}^{n} |a_{k}|e^{k} \int\limits_{0}^{k} \frac{n^{np+p-1}}{(p-1)!}dx \le \sum\limits_{k=0}^{n} |a_{k}|e^{k} \frac{n^{np+p}}{(p-1)!} \]Al crescere di \(p\) l’ultimo membro tende a zero. Quindi l’ipotesi iniziale che \(e\) sia un numero algebrico ha portato ad una contraddizione.
Nei passaggi precedenti abbiamo utilizzato la seguente stima della funzione \(h(x)\):
valida per \(0 \le x\le n\).
6) Il numero pi greco e il teorema di Lindemann
Nel 1882 il matematico tedesco Lindemann (1852-1939) ha dimostrato la trascendenza del numero \(\pi\), la costante più famosa della matematica. La dimostrazione di Lindemann è stata possibile grazie ai risultati ottenuti in precedenza dal matematico Hermite, il quale aveva già dimostrato la trascendenza della costante di Eulero. Il seguente teorema di Hermite è il preludio al teorema successivo di Lindemann:
Teorema 6.1 – Hermite
Il numero \(e^{ r}\) è trascendente per ogni numero razionale \(r\) non nullo.
Il teorema di Lindemann è un’estensione del teorema di Hermite:
Teorema 6.2 – Lindemann
Il numero \(e^{\alpha}\) è trascendente per ogni numero algebrico reale o complesso non nullo \(\alpha\).
La dimostrazione del teorema è lunga e complessa. Per il dettaglio vedere il libro di Baker.
Una conseguenza immediata è il seguente teorema:
Teorema 6.3
Il numero \(\pi\) è trascendente.
Dimostrazione
Se \(\pi\) fosse algebrico, allora lo stesso sarebbe il numero \(i\pi\), in quanto il prodotto di due numeri algebrici è algebrico. Ma allora per il teorema di Lindemann il numero \(e^{i\pi}\) sarebbe trascendente. Questo tuttavia non è possibile poiché per la formula di Eulero si ha
Il teorema di Lindemann diede finalmente soluzione al problema millenario relativo alla possibilità di quadratura del cerchio, utilizzando solo riga e compasso. Questo problema era stato posto dai Greci e aveva impegnato i migliori matematici per la sua soluzione, senza successo.
Il matematico francese Wantzel (1814-1848) aveva dimostrato che i numeri costruibili con riga e compasso sono un sottoinsieme dei numeri algebrici. Dato un cerchio di raggio \(1\), la sua area è uguale a \(\pi\). Per quadrare il cerchio bisogna costruire un lato di lunghezza uguale a \(\sqrt{\pi}\). Ma poiché \(\pi\) è trascendente, lo è anche \(\sqrt{\pi}\) e quindi il cerchio non può essere quadrato.
Nel \(1888\) il matematico tedesco Karl Weierstrass (1815-1897) dimostrò un risultato più generale, già ipotizzato da Lindemann:
Teorema 6.4 – Lindemann-Weierstrass
Siano \(\alpha_{1},\alpha_{2}, \cdots, \alpha_{n}\) numeri algebrici distinti. Allora i numeri
sono linearmente indipendenti sui numeri algebrici. In altre parole, se \(\beta_{1},\beta_{2}, \cdots, \beta_{n}\) sono numeri algebrici non nulli allora risulta
\[ \sum\limits_{k=1}^{n}\beta_{k}e^{\alpha_{k}} \neq 0 \]Per una dimostrazione vedere il testo di Baker. Una conseguenza immediata è il seguente teorema:
Teorema 6.5
Siano \(\alpha_{1},\alpha_{2}, \cdots, \alpha_{n}\) numeri algebrici distinti non nulli. Allora dati \(n\) numeri algebrici non nulli qualsiasi \(\beta_{1},\beta_{2}, \cdots, \beta_{n}\) , il numero
è trascendente.
Vediamo alcune conseguenze del teorema di Lindemann-Weierstrass.
Corollario 6.1
Il numero di Eulero \(e\) è trascendente.
Corollario 6.2
La curva \(e^{x}\) non passa in nessun punto algebrico del piano, ad eccezione del punto \((0,1)\).
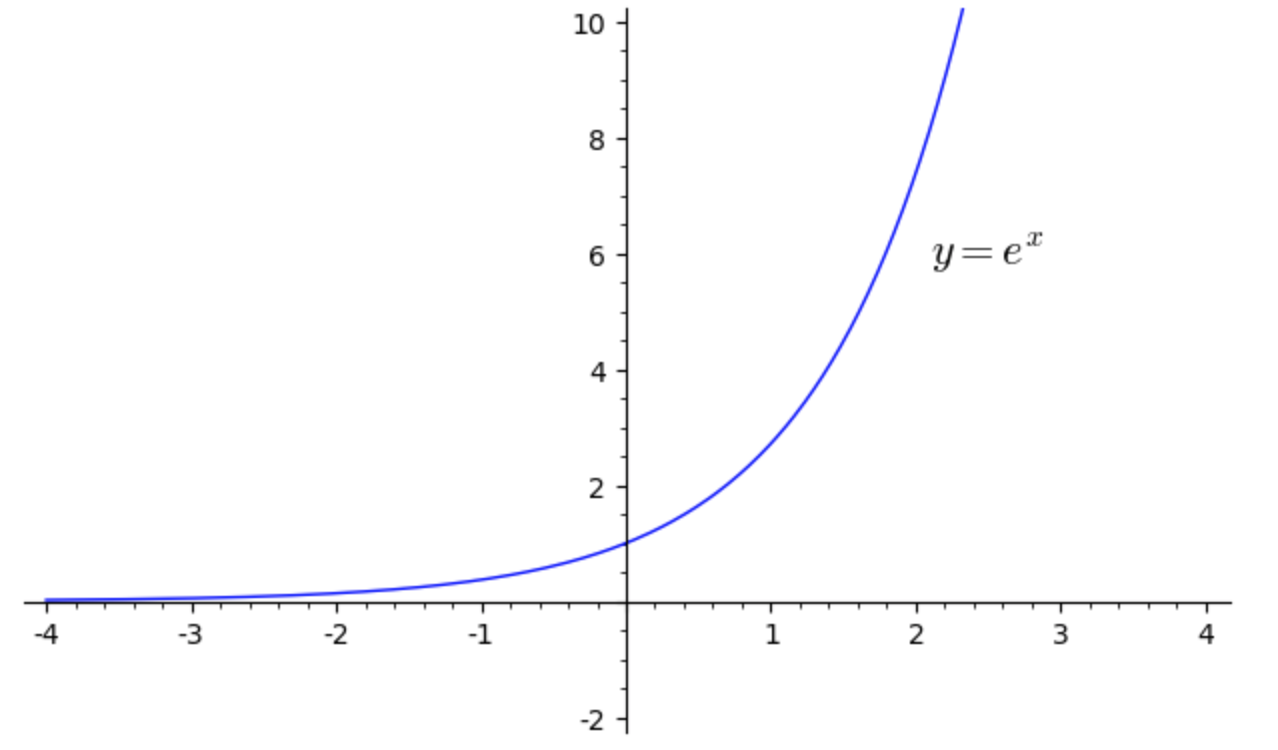
L’insieme dei numeri algebrici è denso nel piano. Ciononostante la curva esponenziale, definita su tutto l’asse reale, riesce ad evitare ciascuno di questi punti, ad eccezione del punto \((0,1)\). In particolare la curva non passa in nessuno dei punti del reticolo piano degli interi.
Corollario 6.3
Se \(\alpha\) è un numero algebrico non nullo, allora \(\sin \alpha\) è trascendente.
Suggerimento
Ricordare la formula
Corollario 6.4
La curva \(y=\sin x\) non passa in nessun punto algebrico del piano, ad eccezione del punto \((0,0)\).
Corollario 6.5
Se \(\alpha\) è un numero algebrico non nullo \(\neq 1\), allora \(\ln \alpha\) è trascendente.
7) Il settimo problema di Hilbert e il teorema di Gelfond-Schneider
In occasione del Secondo Congresso Internazionale dei Matematici tenuto a Parigi nel \(1900\), il matematico tedesco David Hilbert (1862-1943 ) espose \(23\) importanti problemi che avrebbero rappresentato una sfida per tutti i matematici del nuovo secolo. Riuscire a risolvere uno di questi problemi sarebbe stato un motivo di grande orgoglio e avrebbe permesso di far parte della ‘Honors class‘ dei matematici, come disse H. Weyl, uno degli studenti di Hilbert.
Molti dei problemi sono stati risolti, mentre altri, come l’ipotesi di Riemann, rimangono ancora irrisolti. Per una esposizione dettagliata dei problemi di Hilbert vedere [4].
Il problema n. \(7\) di Hilbert riguarda l’espressione \(\alpha^{\beta}\), dove \(\alpha\) è un numero algebrico diverso da \(0,1\) e \(\beta\) è un numero irrazionale algebrico. Il problema consiste nel dimostrare che \(\alpha^{\beta}\) è trascendente.
Congettura di Hilbert
Dato un numero algebrico \(\alpha \neq 0,1\) e un numero algebrico \(\beta\) irrazionale. Allora il numero \(\alpha^{\beta}\) è trascendente.
La risposta alla domanda di Hilbert è positiva. Infatti il problema venne risolto nel \(1934\) dai matematici Alexander Gelfond (1906-1968) e Theodor Schneider (1911-1988), i quali hanno dimostrato il seguente teorema:
Teorema 7.1 – Gelfond-Schneider
Supponiamo che \(\alpha\) e \(\beta\) siano due numeri algebrici, con \(\alpha \neq 0,1\) e \(\beta\) numero non razionale. Allora il numero \(\alpha^{\beta}=e^{\beta (\ln \alpha)}\) è trascendente.
I numeri \(\alpha,\beta\) possono anche essere numeri complessi. Una forma equivalente è la seguente:
Teorema 7.2
Siano \(\beta,\gamma\) due numeri complessi non nulli , con \(\beta\) irrazionale. Allora almeno uno dei tre numeri \(\beta\), \(e^{\gamma}\),\(e^{\gamma \beta}\) è un numero trascendente.
Un’altra forma equivalente è la seguente:
Teorema 7.3
Siano \(\alpha_{1},\alpha_{2}\) due numeri algebrici non nulli tali che il rapporto \(\dfrac{\ln \alpha_{1}}{\ln \alpha_{2}}\) è irrazionale. Allora questo rapporto è un numero trascendente.
Esercizio 7.1
Mediante il teorema di Gelfond-Schneider dimostrare la trascendenza dei seguenti numeri:
Suggerimento
Ricordare la formula di Eulero \(e^{i \pi}=-1\).
Il numero \(2^{\sqrt{2}} \approx 2,6651441\) viene chiamato costante di Gelfond-Schneider. La trascendenza di questo numero era stata già dimostrata da Kuzmin nel 1930, prima del teorema di Gelfond-Schneider.
Esercizio 7.2
Dimostrare che il numero
è trascendente.
Soluzione
Il numero \(\alpha\) è chiaramente irrazionale. Inoltre \(2^{\alpha}=3\).
I teoremi precedenti sono stati generalizzati da Baker nel 1966.
Teorema 7.4 – Baker
Siano \(\alpha_{1},\alpha_{2},\cdots,\alpha_{n}\) numeri algebrici non nulli tali che i numeri \(\ln \alpha_{1},\ln \alpha_{2},\cdots,\ln \alpha_{n}\) siano linearmente indipendenti sul campo dei numeri razionali \(\mathbb{Q}\). Inoltre \(\beta_{0},\beta_{1},\beta_{2},\cdots,\beta_{n}\) siano numeri algebrici non tutti nulli. Allora il numero
è trascendente.
Questo teorema estende sia il teorema di Lindemann-Weirstrass sia il teorema di Gelfond-Schneider.
Nonostante i grandi progressi ottenuti grazie ai teoremi di Hermite, Lindemann, Weierstrass, Baker e altri, resta ancora molto da scoprire. Ci sono molti numeri importanti, per i quali non si è ancora riusciti a dimostrare neanche se sono razionali o irrazionali. Ad esempio i seguenti numeri:
Conclusione
La teoria dei numeri trascendenti, iniziata con gli studi di Eulero e Liouville, è ormai diventata una branca importante della Teoria dei Numeri. I risultati raggiunti, come i teoremi di Lindemann-Weierstrass e di Gelfond-Schneider, hanno una importanza fondamentale, ed anche una grande bellezza, per coloro che comprendono la matematica. Resta ancora molto da scoprire e sicuramente non sono escluse in futuro applicazioni importanti anche in settori diversi dalla Matematica.
Bibliografia
[1]S. Lipschutz – Schaum’s Outline of Set Theory (McGraw-Hill)
[2]F. Jarvis – Algebraic Number Theory (Springer)
[3]A. Baker – Transcendental Number Theory (Cambridge University Press)
[4]B. Yandell – The Honors Class: Hilbert’s Problems and Their Solvers (A.K. Peters)
[5]P. Erdos – Representations of real numbers as sums and products of Liouville numbers (Michigan Math, 1962)
[6]S. Miller, R. Takloo-Bighash – An Invitation to Modern Number Theory (Princeton)

0 commenti