L’insieme dei numeri reali \(\mathbb{R}\) è la base sulla quale sono costruiti i principali settori dell’analisi matematica classica: il calcolo differenziale e integrale, le equazioni differenziali, il calcolo delle probabilità, ecc. Come è noto l’insieme di numeri reali è costituito da due grandi sottoinsiemi:
- l’insieme dei numeri razionali \(\mathbb{Q}\)
- l’insieme dei numeri irrazionali \(\mathbb{R}-\mathbb{Q}\)
I numeri reali sono associati strettamente all’esigenza di misurare le dimensioni degli oggetti: lunghezze, aree, volumi, ecc. Mentre è abbastanza facile stabilire le dimensioni di oggetti espresse con numeri naturali, o più in generale con i numeri razionali, è invece molto più difficile assimilare il concetto di numero irrazionale. I numeri irrazionali hanno infinite cifre decimali, e quindi è più difficile percepire il valore esatto. Tuttavia i numeri irrazionali hanno una importanza fondamentale per l’Analisi matematica; senza di essi non avremmo la continuità dei numeri reali e la corrispondenza biunivoca con i punti della retta geometrica.
1) Numeri razionali
Definizione 1.1
Un numero razionale \(x\) è un numero che può essere rappresentato come quoziente fra due numeri interi. Cioè
Diremo che la rapresentazione è in forma ridotta se \((a,b)=1\).
Chiaramente l’insieme dei numeri razionali contiene anche i numeri interi, ponendo \(b=1\).
Esempio 1.1
Sono numeri razionali i seguenti:
1.1) Espansione decimale dei numeri razionali
Effettuando la divisione otteniamo lo sviluppo decimale dei numeri razionali. Ad esempio:
\[ \begin{array}{l} \dfrac{1}{2}=0,5 \\ \dfrac{1}{40}=0,025 \\ \dfrac{1}{3}=0,3333 \cdots \\ \dfrac{9}{11}=0,8181 \cdots \\ \dfrac{1}{24}=0,0416666 \cdots \\ \end{array} \]Come si vede l’espansione decimale può essere finita oppure illimitata periodica. Nel secondo caso il numero viene detto numero decimale periodico.
Si può dimostrare il seguente teorema:
Teorema 1.1
Un numero razionale scritto in forma ridotta \(x=\dfrac{a}{b}\) ha uno sviluppo decimale finito se e solo se gli unici fattori primi di \(b\) sono \(2\) e \(5\).
Dimostrazione
Supponiamo \(b=2^{n}5^{m}\). Allora se \(m \le n\) abbiamo:
Il numeratore \(5^{n-m}a\) è un numero intero e quindi per effettuare la divisione basta che mettiamo la virgola decimale al posto giusto.
In modo analogo si ragiona nel caso \(m \gt n\).
Naturalmente se il denominatore \(b\) è divisibile per qualche numero primo diverso da \(2\) e da \(5\), allora è facile vedere che la divisione non termina.
Si può dimostrare il seguente teorema:
Teorema 1.2
Ogni numero razionale si può esprimere come numero decimale finito oppure numero decimale periodico.
Vale anche il contrario: ogni sviluppo decimale finito o periodico rappresenta un numero razionale.
Per rappresentare lo sviluppo decimale periodico utilizziamo la seguente notazione:
\[ \begin{array}{l} \dfrac{1}{3}=0,3333 \cdots = 0,\overline{3} \\ \dfrac{1}{7}=0,142857142857 \cdots = 0,\overline{142857} \\ \dfrac{3}{11}=0,272727 \cdots = 0,\overline{27} \\ \end{array} \]Vediamo con un esempio come determinare il numero razionale corrispondente ad uno sviluppo decimale periodico.
Esercizio 1.1
Convertire il numero \(x=0,35 \overline{7}\) nella forma razionale \(x=\dfrac{a}{b}\).
Soluzione
Effettuiamo i seguenti calcoli:
È chiaro come funziona l’algoritmo per una espansione decimale qualsiasi.
Osserviamo infine che anche i numeri decimali finiti possono essere espressi tramite numeri decimali periodici. Vediamo alcuni esempi:
1.2) Rappresentazione di un numero razionale come somma di frazioni unitarie
Definizione 1.2
Si chiamano frazione egizie le frazioni con il numeratore unitario, cioè della forma \(\dfrac{1}{n}\). In altri termini sono i reciproci dei numeri interi positivi.
Il nome deriva dal fatto che gli antichi Egizi utilizzavano somme formate da tali frazioni per rappresentare i numeri razionali.
Nel famoso papiro di Rhind (vedi Wikipedia) sono presenti delle tabelle di frazioni che permettono di decomporre un numero razionale in somma di frazioni unitarie. Ad esempio
L’algoritmo di Fibonacci-Sylvester
Esistono diversi metodi per scomporre un numero razionale in somma di frazioni egizie. In questo articolo analizziamo il metodo ideato da Leonardo Pisano (1170 ca – 1230), meglio noto come Fibonacci. ll metodo di Fibonacci è stato in seguito approfondito da Sylvester (1814-1897), che ha anche dimostrato la sua correttezza.
Siano dati due interi positivi \(a,b\), con \(0 \lt a \lt b\) e quindi
Poiché \(\dfrac{b}{a} \gt 1\), esiste un intero \(n_{1}\) tale che \(n_{1}-1 \lt \dfrac{b}{a} \le n_{1}\) e quindi
\[ \frac{1}{n_{1}} \le \frac{a}{b} \lt \frac{1}{n_{1}-1} \]Da questo deriva facilmente che che \((n_{1}a – b) \lt a\) e quindi
\[ \frac{a}{b} = \frac{1}{n_{1}}+ \frac{n_{1}a -b}{bn_{1}} \]La frazione \(\dfrac{a_{1}}{b_{1}}=\dfrac{n_{1}a -b}{bn_{1}}\) ha il numeratore minore di \(a\). Se \(a_{1}=1\) abbiamo finito. Altrimenti possiamo ripetere il processo con la nuova frazione \(\dfrac{a_{1}}{b_{1}}\) e così via.
Il processo termina dopo un numero finito di passi, essendo \(a_{i-1} \gt a_{i}\), e quindi otteniamo la seguente rappresentazione
Esercizio 1.2
Dimostrare la seguente decomposizione mediante l’algoritmo di Fibonacci-Sylvester
L’algoritmo di Fibonacci-Sylvester è un esempio di algoritmo greedy, un tipo di algoritmo che procede in modo sequenziale, cercando di fare la scelta ottimale ad ogni passo. Anche se questo metodo non sempre ha successo, tuttavia in molte situazioni si è dimostrato efficace. Un esempio famoso è l’algoritmo di Dijkstra per la ricerca del cammino più breve fra due nodi di un grafo.
Esistono anche altri algoritmi per la riduzione di un numero razionale a somma di frazioni unitarie. L’algoritmo di Fibonacci-Sylvester ha il vantaggio della sua semplicità, ma non è sempre ottimale. Un esempio famoso è dato dal numero \(\dfrac{5}{121}\), per il quale il metodo di Fibonacci-Sylvester da una rappresentazione con denominatori molto grandi (vedere i dettagli su Wikipedia), mentre con altri metodi si hanno espressioni più semplici.
2) La scoperta dei numeri irrazionali
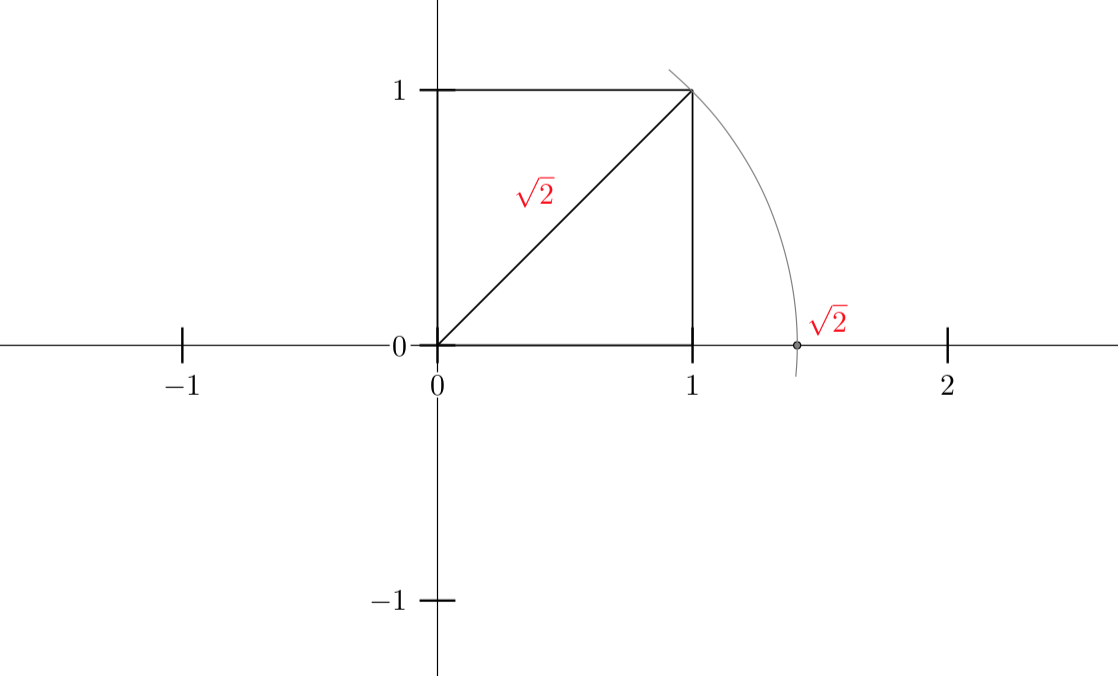
Un numero irrazionale è un numero reale che non può essere espresso come rapporto fra due numeri interi. I numeri irrazionali hanno una rappresentazione decimale con un numero infinito di cifre, senza periodicità. Il primo numero irrazionale scoperto dai Greci è \(\sqrt{2}\), la lunghezza della diagonale del quadrato di lato unitario.
I Pitagorici affermavano che tutte le cose sono costituite da numeri, e quindi l’universo ha una struttura geometrica misurabile. Tutte le cose potevano essere spiegate mediante relazioni fra numeri interi e i loro rapporti. Il loro motto era “Tutto è numero”.
Il loro modello venne messo in crisi dalla scoperta che alcuni rapporti (ad esempio quello tra la diagonale e il lato di un quadrato) non sono esprimibili mediante numeri interi. Secondo la tradizione la scoperta venne fatta da Ippaso di Metaponto, anche se non tutti sono d’accordo. Ippaso venne considerato un traditore, per aver reso pubblico un risultato che metteva in crisi la dottrina della scuola pitagorica. Il suo tradimento fu così grave che i pitagorici gli costruirono un tomba a Metaponto, quando era ancora in vita. Secondo altri Ippaso venne gettato in mare dai componenti della scuola pitagorica.
2.1) Grandezze commensurabili e incommensurabili
I numeri per i matematici della Grecia antica erano sostanzialmente i numeri naturali. Essi distinguevano i numeri naturali dalle grandezze, utilizzate per rappresentare le misure degli oggetti geometrici (lunghezze, aree, volumi). Tuttavia studiando i rapporti fra le grandezze, di fatto conoscevano anche quelli che oggi chiamiamo numeri razionali.
Supponiamo di rappresentare i numeri sulla retta, in cui è fissato un punto origine \(O\), corrispondente al numero \(0\), e una unità di misura:
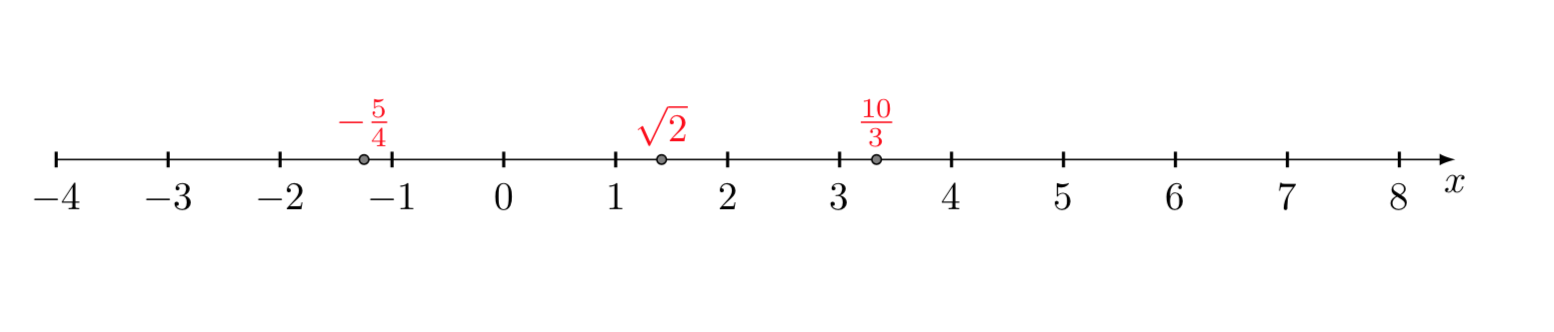
A prima vista possiamo supporre una corrispondenza biunivoca fra numeri (naturali e razionali) e i punti della retta. Ogni numero è rappresentato da un punto sulla retta e viceversa ogni punto \(P\) della retta corrisponde al numero che misura la lunghezza del segmento \(OP\) (se il numero è negativo naturalmente prendiamo il suo valore assoluto).
Sicuramente ogni numero razionale è rappresentato da un punto della retta. Possiamo chiederci se è vero anche il contrario: cioè se ad ogni punto della retta corrisponde un numero razionale.
Una proprietà fondamentale dei numeri razionali, che li distingue dagli interi, è che formano un insieme denso, cioè fra due numeri razionali \(a,b\) è sempre possibile trovarne un altro all’interno dell’intervallo; basta prendere il numero \(\dfrac{a+b}{2}\). Questo implica che in un qualsiasi intervallo della retta reale, esistono infiniti numeri razionali. Quindi verrebbe da concludere che i numeri razionali coprano completamente la retta, cioè ad ogni punto della retta possiamo far corrispondere un numero razionale.
In termini equivalenti possiamo pensare che per ogni segmento è possibile fissare una unità di misura tale che la lunghezza del segmento è un multiplo intero di questa, e quindi ogni misura può essere espressa con un numero razionale.
I Greci chiamavano commensurabili due lunghezze per le quali è possibile trovare una unità di misura comune, cioè in modo equivalente se il rapporto delle loro misure è un numero razionale.
La scoperta che il lato e la diagonale di un quadrato non sono grandezze commensurabili pose in crisi la teoria pitagorica e diede inizio allo studio delle grandezze incommensurabili e quindi dei numeri irrazionali.
2.2) Il Libro X degli Elementi di Euclide
Il Libro X degli Elementi di Euclide è dedicato alla definizione delle grandezze commensurabili e incommensurabili. Il modo di esposizione è diverso da quello moderno, e utilizza la terminologia geometrica. Riportiamo soltanto alcune definizioni di Euclide.
Definizione X.1.
Si dicono grandezze commensurabili quelle che sono misurate da una stessa misura, e incommensurabili quelle per le quali non può esistere una misura comune.
Definizione X.2.
Sono commensurabili in potenza lerette tali che i quadrati su esse costruiti possono essere misurati da una stessa area, ed incommensurabili in potenza se i loro quadrati non ammettono nessuna area come misura comune.
In termini algebrici queste definizioni significano che due numeri \(a,b\) sono commensurabili se il rapporto è un numero razionale, altrimenti sono incommensurabili.
Il libro X degli Elementi contiene \(115\) proposizioni ed è uno dei più lunghi e difficili. Fibonacci lo definì ‘difficilior est antecedentium et quorumdam sequentium librorum Euclidis‘. Lo stesso Stevino (1548-1620) lo trovò difficile da decifrare e lo definì «la croix des mathématiciens» .
Tuttavia vale la pena dedicare del tempo per studiare e comprendere le varie proposizioni di Euclide, che dimostrano l’alto livello di rigore matematico raggiunto dai Greci.
2.3) L’algoritmo di Euclide e le grandezze commensurabili
Come è noto l’algoritmo di Euclide è utilizzato per calcolare il massimo comune divisore fra due interi. Tuttavia può esser applicato a due numeri qualsiasi, anche non interi. Se applichiamo l’algoritmo a due grandezze \(a,b\), allora sono possibili due casi:
- Se le due grandezze sono commensurabili, l’algoritmo termina dopo un numero finito di passi.
- Se le due grandezze sono incommensurabili, l’algoritmo non termina.
Ricordiamo inoltre che l’algoritmo di Euclide viene anche utilizzato per determinare la frazione continua corrispondente ad un numero reale. Come è noto la frazione continua è finita se e solo se il numero è razionale, altrimenti è infinita (vedi articolo sulle frazioni continue in questo sito).
2.4) L’irrazionalità di \(\sqrt{2}\)
In base al teorema di Pitagora, la lunghezza della diagonale di lato unitario misura \(\sqrt{2}\), come si vede nella figura seguente:
Teorema 2.1
\(\sqrt{2}\) è un numero irrazionale.
Riportiamo la dimostrazione classica di Euclide.
Supponiamo che \(\sqrt{2}=\dfrac{a}{b}\) con \(a,b \in\mathbb{Z}\) e \((a,b)=1\). Allora
e quindi \(2|a\). Essendo \(a\) un numero pari, possiamo porre \(a=2k\) ottenendo
\[ a^{2}=4k^{2}=2b^{2} \]e quindi
\[ 2k^{2}=b^{2} \]da cui deriva che \(2|b\), contrariamente all’ipotesi che \((a,b)=1\).
Si può dare anche una dimostrazione geometrica, utilizzando la figura seguente:
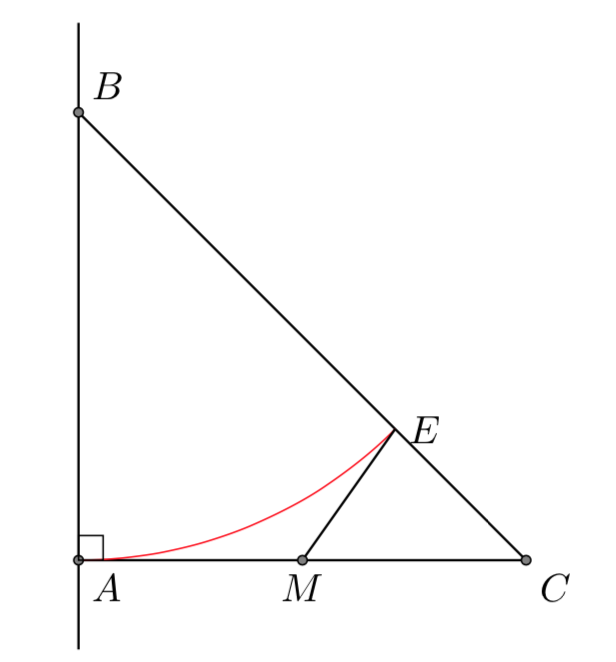
Supponiamo di avere un triangolo rettangolo isoscele con \(\overline{AC}=\overline{AB}=b,\overline{BC}=a\).
Dalla figura vediamo che anche il triangolo MEC è rettangolo e isoscele. Poiché \(\overline{EC}=\overline{EM}=a-b\) e l’ipotenusa vale \(\overline{MC}=b-(a-b)=2b-a\) anche il nuovo triangolo ha i lati interi, di lunghezza inferiore. Questo processo può essere continuato all’infinito portando ad una contraddizione, in quanto le grandezze intere non possono diventare minori di \(1\).
Con un ragionamento simile si può stabilire l’irrazionalità dei numeri \(\sqrt{n^{2}+1}\) per ogni intero \(n \gt 1\). Basta prendere un triangolo rettangolo con i lati lunghi \(1\) e \(n\).
Mediante un ragionamento simile, possiamo dimostrare il seguente teorema:
Teorema 2.2
Dato un intero positivo \(n\) che non sia un quadrato perfetto, allora la sua radice quadrata \(x=\sqrt{n}\) è un numero irrazionale.
Naturalmente esistono diverse dimostrazioni dell’irrazionalità di \(\sqrt{n}\). Per una dimostrazione originale che non utilizza i concetti di divisori di un intero vedere [1].
Teorema 2.3
Se un intero positivo \(n\) non è una potenza k-esima con \(k\) intero e \(k \gt 1\), allora
è un numero irrazionale
Dimostrazione
Ss fosse razionale potremmo scrivere
La dimostrazione del teorema può essere completata facilmente utilizzando il teorema fondamentale dell’aritmetica: se \(n\) non è una potenza k-esima, allora esiste un numero primo nella sua decomposizione il cui esponente non è divisibile per \(k\).
3) La teorie degli insiemi di Cantor e i numeri reali
L’insieme dei numeri reali \(\mathbb{R}\) è definito come l’unione dei numeri razionali e dei numeri irrazionali.
Un principio fondamentale della geometria analitica è la corrispondenza biunivoca fra l’insieme dei numeri reali e i punti della retta euclidea, una volta fissati l’orientamento della retta, l’origine e una unità di misura. In un riferimento cartesiano il numero reale che corrisponde ad un punto \(P\) della retta viene chiamata ascissa del punto. Ogni punto della retta corrisponde quindi ad un numero razionale oppure ad un numero irrazionale.
Nel corso del XIX secolo il matematico tedesco George Cantor (1845-1918) ha sviluppato la teoria della cardinalità degli insiemi infiniti, che ha rappresentato una svolta molto importante nello studio dei fondamenti della Matematica. La teoria sviluppata da Cantor si occupa della classificazione degli insiemi, in base al numero di elementi che contengono. Nel caso di un insieme finito la cardinalità coincide con il numero degli elementi dell’insieme. Nel caso di insiemi infiniti la situazione è più complessa. Per classificare gli insiemi infiniti Cantor propose la seguente definizione:
Definizione 3.1
Due insiemi \(A\) e \(B\) hanno la stessa cardinalità se esiste una corrispondenza biunivoca fra di essi.
È evidente che due insiemi finiti hanno la stessa cardinalità se e solo se hanno lo stesso numero di elementi. La novità principale di Cantor è che le cardinalità degli insiemi infiniti possono essere diverse fra loro, distinguendo quindi vari livelli di infinito.
Il primo livello di infinito è costituito dall’insieme dei numeri naturali \(\mathbb{N}=\{1,2,3, \cdots \}\) e da tutti gli insiemi che sono in corrispondenza biunivoca con questo insieme. Tutti questi insiemi vengono chiamati numerabili e la loro cardinalità viene indicata con la lettera ebraica \(\aleph_{0}\) (aleph-zero).
Esempio 3.1
I seguenti insiemi sono numerabili:
È facile dimostrare che anche l’insieme dei numeri razionali \(\mathbb{Q}\) è numerabile, cioè può essere messo in corrispondenza biunivoca con l’insieme dei numeri naturali \(\mathbb{N}\). Per convincersi basta scrivere i numeri razionali nella seguente sequenza:
\[ \begin{array}{l} \dfrac{0}{1}; \dfrac{1}{1}; \dfrac{-1}{1}; \\ \dfrac{1}{2}; \dfrac{-1}{2}; \dfrac{2}{1};\dfrac{-2}{1}; \\ \dfrac{1}{3}; \dfrac{2}{3}; \dfrac{-1}{3};\dfrac{-2}{3}; \dfrac{3}{1}; \dfrac{3}{2}; \dfrac{-3}{1};\dfrac{-3}{2}; \\ \vdots \\ \end{array} \]Nella sequenza vengono scritti tutti i numeri razionali; inoltre possiamo definire una corrispondenza biunivoca assegnando ad ogni numero razionale la sua posizione nella sequenza, cioè un numero naturale.
Il livello successivo di infinito è costituito dagli insiemi che non sono numerabili ma sono in corrispondenza biunivoca con i numeri reali, per i quali si dice che hanno la potenza del continuo. Infatti, nel 1873 Cantor ha dimostrato che l’insieme dei numeri reali \(\mathbb{R}\) non è numerabile.
Teorema 3.1
L’insieme dei numeri reali non è numerabile.
Da questo ne deriva che l’insieme dei numeri irrazionali non è numerabile.
Per questa dimostrazione (vedi link) ha utilizzato il famoso procedimento diagonale, che oggi viene utilizzato e accettato da gran parte dei matematici, anche se è stato oggetto di critiche da importanti matematici: Kronecker, Poincaré, Weyl, Brouwer e altri. Per una interessante storia della teoria degli insiemi vedere [2].
Esercizio 3.1
Dimostrare che i seguenti insiemi hanno la potenza del continuo:
4) Proprietà dei numeri reali
I numeri irrazionali sono caratterizzati dal fatto di avere una rappresentazione decimale illimitata non periodica. Consideriamo due numeri irrazionali con rappresentazioni decimali diverse almeno per una cifra:
\[ \begin{array}{l} x = 12,349217 \cdots \\ y = 12,349218 \cdots \end{array} \]Indichiamo con \(r\) il numero razionale \(r=12,349218\). È evidente che i due numeri irrazionali \(x,y\) sono distinti, in quanto vale la seguente diseguaglianza
\[ x \lt r=12,349218 \lt y \]Quindi possiamo enunciare il seguente teorema:
Teorema 4.1
Ogni numero irrazionale ammette un’unica rappresentazione decimale infinita non periodica
Diversamente dai razionali, l’insieme dei numeri irrazionali non costituisce un gruppo rispetto alle operazioni di addizione o moltiplicazione, in quanto la somma o il prodotto di due numeri irrazionali può essere un numero razionale. Ad esempio \( \sqrt{2} \sqrt{8}=4\), oppure \(\sqrt{2}-\sqrt{2}=0\).
Tuttavia vale il seguente teorema:
Teorema 4.2 – Proprietà di chiusura
Sia \(\alpha\) un numero irrazionale e \(t\) un numero razionale non nullo. Allora sono irrazionali i seguenti numeri:
Teorema 4.3
Dati due numeri reali \(a \lt b\), esiste un numero razionale \(r\) tale che
Dimostrazione
Supponiamo inizialmente che \(b \gt 0\). Scegliamo un intero positivo \(n\) tale che \(b-a \gt \dfrac{1}{n}\). Ovviamente più \(a,b\) sono vicini, maggiore deve essere il valore di \(n\). Indichiamo con \(m\) il più piccolo intero positivo tale che \(b \le \dfrac{m}{n}\). Si può verificare facilmente che il numero razionale \(r=\dfrac{m-1}{n}\) è compreso fra i due numeri reali \(a,b\). La dimostrazione si estende senza difficoltà al caso \(b \le 0\).
Teorema 4.4
Dati due numeri reali \(a \lt b\), esiste un numero irrazionale \(s\) tale che
Dimostrazione
Per il teorema precedente esiste un numero razionale \(r\) tale che
Poniamo \(s=r+\sqrt{2}\). Per il teorema 4.2 \(s\) è un numero irrazionale, chiaramente compreso fra i due numeri reali \(a,b\).
4.1) L’approssimazione diofantea
L’approssimazione diofantea è la branca della teoria dei numeri che si occupa di studiare l’approssimazione dei numeri irrazionali mediante numeri razionali. Uno dei metodi più efficienti dell’approssimazione diofantea è costituito dalle frazioni continue (vedi articolo in questo blog).
Come abbiamo visto l’insieme dei numeri razionali è denso sulla retta reale. Quindi per ogni numero reale \(\alpha\) e fissato un valore piccolo a piacere \(\epsilon\), esiste sempre un numero razionale \(\dfrac{p}{q}\) tale che
Possiamo dare la seguente definizione:
Definizione 4.1
Un numero irrazionale \(\alpha\) ha un’approssimazione razionale di ordine \(n\) se esiste una grandezza \(K(\alpha)\), dipendente solo da \(\alpha\), tale che la disuguaglianza
ha infinite soluzioni.
Notiamo che se \(\alpha\) è un numero razionale \(\dfrac{a}{b}\), allora abbiamo
\[ \left|\frac{a}{b} – \frac{p}{q}\right|= \frac{|aq-bp|}{bq} \ge \frac{1}{bq} \]e quindi la differenza non può essere inferiore ad una certa soglia.
Se invece \(\alpha\) è irrazionale, allora esistono infiniti numeri razionali \(\dfrac{p}{q}\) che soddisfano la disuguaglianza
Vale infatti il seguente teorema:
Teorema 4.5 – Hurwitz
Dato un numero irrazionale \(\alpha\), esistono infiniti numeri razionali \(\dfrac{p}{q}\) tali che
Se sostituiamo \(\sqrt{5}\) con un numero più grande, allora esistono infiniti numeri irrazionali per i quali la disuguaglianza è verificata al massimo da un numero finito di frazioni.
Il classico contro-esempio è rappresentato dal numero \(x=\dfrac{1+\sqrt{5}}{2}\).
Per una dimostrazione del teorema di Hurwitz vedere [3]. Per una esposizione completa dell’approssimazione diofantea vedere [4].
5) Esempi di numeri irrazionali
5.1) Le radici dei polinomi
Teorema 5.1
Se un polinomio con coefficienti interi
ha una soluzione razionale \(\dfrac{a}{b}\), con \(a,b\) interi primi fra loro, allora
\[ a| c_{0} \quad \text{e} \quad b|c_{n} \\ \]Dimostrazione
Sostituiamo \(x\) con \(\dfrac{a}{b}\) e moltiplichiamo per \(b^{n-1}\). Vediamo che \(\dfrac{c_{n}a^{n}}{b}\) è un intero, e quindi \(b|c_{n}\) poiché per ipotesi \((a,b)=1\). Se invece sostituiamo \(x\) con \(\dfrac{a}{b}\) e moltiplichiamo per \(\dfrac{b^{n}}{a}\) vediamo che \(\dfrac{c_{0}b^{n}}{a}\) è un intero, e quindi \(a|c_{0}\).
Nel caso \(c_{n}=\pm 1\), se esiste una soluzione razionale, allora tale soluzione è un intero che divide \(c_{0}\).
Inoltre nel caso particolare del polinomio \(x^{n}=c\), le sole soluzioni razionali sono intere, e questo capita solo se \(c\) è la potenza n-esima di un intero.
Questo teorema conferma quindi che i numeri del tipo \(\sqrt[n]{x}\) sono irrazionali, tranne nel caso in cui \(x\) è una potenza n-esima.
Esercizio 5.1
Dimostrare che \(\cos 20^{0}\) è irrazionale.
Suggerimento
Sfruttare l’identità trigonometrica \(\cos 3\alpha=4\cos^{3}\alpha – 3 \cos \alpha\) e risolvere l’equazione algebrica.
Esercizio 5.2
Dimostrare che \(\log_{10} 2\) è irrazionale.
5.2) Il numero di Eulero \(e\)
Il numero di Eulero \(e\) può essere così definito:
\[ e = \lim_{n \to \infty}\left(1+\frac{1}{n}\right)^{n} \approx 2,718281\cdots \]Una definizione equivalente è la seguente:
\[ e = 1 + \frac{1}{1!} +\frac{1}{2!} +\frac{1}{3!} + \frac{1}{4!} + \cdots \\ \]Si tratta di un numero irrazionale e trascendente. È una delle costanti fondamentali che appare in molte equazioni della matematica pura e applicata. Venne introdotto dal matematico John Napier(1550 – 1617) come base dei logaritmi naturali; l’indicazione della lettera “e” è dovuta ad Eulero.
Il numero venne scoperto da Jacob Bernoulli mentre studiava il problema del calcolo dell’interesse composto da corrispondere a fronte di un prestito.
L’irrazionalità di \(e\) venne dimostrata inizialmente da Eulero in 1744.
Teorema 5.2
Il numero di Eulero è irrazionale.
Dimostrazione
Supponiamo per assurdo che \(e = \dfrac{p}{q}\) sia razionale, dove \(p,q\) siano interi, con \(q \ge 1\). Ricordando lo sviluppo in serie di \(e\) possiamo scrivere:
Il termine a sinistra è un intero, mentre a destra è la somma di un intero e di un numero positivo strettamente minore di \(1\) in quanto:
\[ \frac{q!}{(q+1)!} + \frac{q!}{(q+2)!} + \cdots + \frac{q!}{(q+n)!} + \cdots \lt \frac{1}{2}+ \frac{1}{2^{2}}+ \cdots + \frac{1}{2^{n}} + \cdots = 1 \]Eulero ha dato una dimostrazione alternativa utilizzano lo sviluppo della frazione continua di \(e\):
\[ e = [2;1,2,1,1,4,1,1,6,1, \cdots ] \]Poiché la frazione continua non è finita, il numero di Eulero non può essere un numero razionale. Per la determinazione della frazione continua di \(e\) vedere il testo di Knuth[5].
Esistono molte dimostrazioni dell’irrazionalità del numero di Eulero. Alcune utilizzano il seguente teorema:
Teorema 5.3
Sia data la seguente funzione
f_{n}(x)= \frac{x^{n}(1-x)^{n}}{n!}=\frac{1}{n!}\sum\limits_{k=n}^{2n}c_{k}x^{k}
\]
dove \(n\) è un intero positivo e \(c_{k}\) è un intero.
La funzione \(f_{n}\) verifica le seguenti proprietà:
f_{n}^{(k)}(0)= 0 \quad \text{se } \quad k \lt n \quad \text{o} \quad k \gt 2n \\ f_{n}^{(k)}(0)= \dfrac{k!}{n!}c_{k} \quad \text{se } n \le k \le 2n \\ \end{array} \]
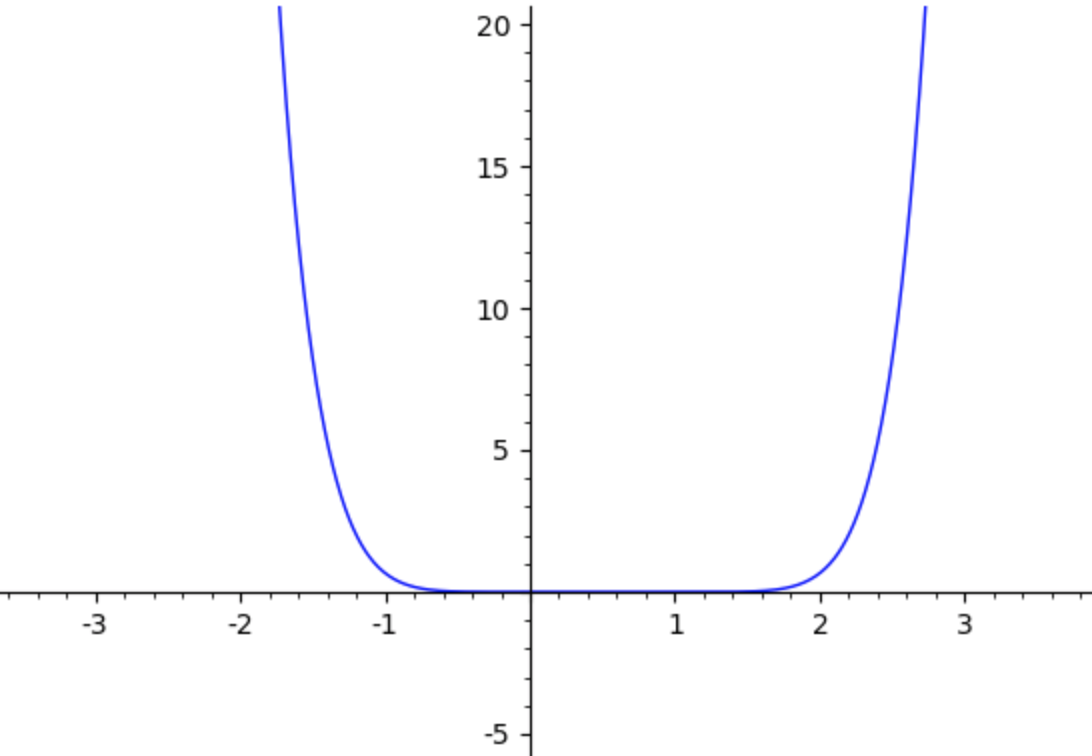
Inoltre notiamo che la funzione è simmetrica rispetto al punto \(x=\dfrac{1}{2}\) e quindi la funzione e tutte le derivate assumono valori interi nei punti \(0,1\).
Mediante le proprietà della funzione precedente è possibile dimostrare il seguente teorema più generale:
Teorema 5.4
Per ogni numero razionale \(t \neq 0\) il numero \(e^{t}\) è irrazionale.
Dimostrazione
Chiaramente è sufficiente dimostrare che \(e^{t}\) non può essere razionale, con \(t\) intero positivo. Supponiamo quindi che \(e^{t}=\dfrac{a}{b}\) sia un numero razionale, con \(a,b,t\) interi positivi. Poniamo
Derivando abbiamo
\[ \frac{d }{dx}(e^{tx}F_{n}(x))= te^{tx}F_{n}(x) + e^{tx}F_{n}^{(1)}(x)= t^{2n+1}e^{tx}f_{n}(x) \\ \]Integrando troviamo
\[ \int_{0}^{1}t^{2n+1}e^{tx}f_{n}(x) dx = \frac{a}{b}F_{n}(1)- F_{n}(0) \\ \]Osserviamo che \(F_{n}(0)\) e \(F_{n}(1)\) sono interi e quindi, moltiplicando l’integrale per \(b\), anche \(aF_{n}(1) – bF_{n}(0)\) è un intero. Utilizzando le proprietà della funzione \(f_{n}(x)\) troviamo la seguente disuguaglianza per \(n\) abbastanza grande:
\[ 0 \lt b \int_{0}^{1}t^{2n+1}e^{tx}f_{n}(x) dx \lt \frac{bt^{2n}e^{t}}{n!} \lt 1 \\ \]Poiché non esiste alcun intero compreso fra \(0\) e \(1\) abbiamo una contraddizione, e quindi l’ipotesi che \(e^{t}\) è razionale è falsa.
5.3) Il numero \(\pi\)
Il numero \(\pi\) deriva dallo studio delle dimensioni del cerchio, essendo il rapporto fra la lunghezza della circonferenza e il diametro. È conosciuto da almeno 4000 anni ed è la costante più nota, anche fuori dal mondo matematico. Si tratta di un numero irrazionale e trascendente. Attualmente, grazie ai computers, si conoscono milioni di cifre decimali del numero \(\pi\). Mediante l’algoritmo euclideo è possibile calcolare i primi elementi della frazione continua infinita corrispondente:
\[ \pi = [3;7,15,1,292,1,1,1,2,\cdots ] \]I primi convergenti di \(\pi\) sono quindi:
\[ \begin{array}{l} [3;] = 3 \\ [3;7]= \dfrac{22}{7}= 3,142857 \\ [3;7,15]= \dfrac{333}{106}= 3,141509 \\ [3;7,15,1]= \dfrac{355}{113}= 3,14159292 \\ [3;7,15,1,292]= \dfrac{103993}{33102}= 3,14159265 \\ \end{array} \]La frazione \(\dfrac{355}{133}\) è un’ottima approssimazione, corretta fino a sei cifre decimali, ed è facile da ricordare. Venne scoperta dal matematico olandese Adrien Metius(1571-1635). Il numero è anche conosciuto come numero di Metius.
L’irrazionalità del numero \(\pi\) è stata dimostrata per primo da Lambert nel 1761, utilizzando la teoria delle frazioni continue, in particolare l’espansione della funzione \(\tan x\).
La dimostrazione di Lambert è abbastanza complessa. Nel seguito seguiremo lo schema di dimostrazione proposto da Niven[3].
Teorema 5.5
I numeri \(\pi\) e \(\pi^{2}\) sono irrazionali.
Dimostrazione
Chiaramente è sufficiente dimostrare che \(\pi^{2}\) è irrazionale. Supponiamo che \(\pi^{2}=\dfrac{a}{b}\) sia un numero razionale, con \(a,b\) interi positivi. Poniamo
Notiamo che \(G_{n}(0)\) e \(G_{n}(1)\) sono interi. Inoltre
\[ \frac{d }{dx}\{G_{n}^{(1)}(x) \sin (\pi x) – \pi G_{n}(x) \cos(\pi x)\} = \\\{G_{n}^{(2)}(x)+\pi^{2}G_{n}(x)\}\sin \pi x= b^{n}\pi^{2n+2}f_{n}(x)\sin (\pi x) = \\
\pi^{2}a^{n} \sin (\pi x) f_{n}(x) \\ \]
Calcoliamo ora l’integrale seguente mediante l’integrazione per parti:
\[ \pi \int_{0}^{1}a^{n} \sin (\pi x)f_{n}(x) dx = G_{n}(0)+G_{n}(1) \ \]Il valore della somma \(G_{n}(0) + G_{n}(1)\) è un intero. Tuttavia per \(n\) abbastanza grande vale la seguente disuguaglianza
\[ 0 \lt \pi \int_{0}^{1}a^{n}\sin (\pi x) f_{n}(x) dx \lt \frac{\pi a^{n}}{n!} \lt 1 \\ \]Abbiamo una contraddizione e quindi l’ipotesi che \(\pi^{2}=\dfrac{a}{b}\) è un numero razionale è falsa.
Si può dimostrare che \(\pi^{n}\) è un numero irrazionale per ogni intero positivo \(n\). Ricordiamo infine che allo stato attuale non è noto se la somma
è un numero razionale o irrazionale.
6) La funzione zeta di Riemann
La funzione zeta di Riemann zeta \(\zeta(s)\) è così definita:
\[ \zeta(s) = \sum\limits_{n=1}^{\infty}\frac{1}{n^{s}} \]dove \(s=\sigma + it\), con \(\sigma \gt 1\).
Il calcolo della funzione zeta negli interi positivi pari è dato dalla formula di Eulero
dove \(B_{n}\) sono numeri razionali, chiamati numeri di Bernoulli. I valori iniziali sono \(B_{0}=1,B_{1}=\dfrac{-1}{2}, B_{2}=\dfrac{1}{6},B_{4}=\dfrac{-1}{30}\). I numeri dispari di Bernoulli sono tutti uguali a zero, ad eccezione di \(B_{1}\).
Dalla formula di Eulero deriva che \(\zeta(2n)\) è un numero irrazionale, per ogni valore di \(n\).
Non esiste una formula simile nel caso di interi positivi dispari. Allo stato attuale è stato dimostrato nel 1979 da Apéry che \(\zeta(3)\) è irrazionale, mentre non è noto se \(\zeta(5)\) o \(\zeta(7\)) sono irrazionali. Tuttavia nel 2000 Rivoal ha dimostrato che tra i valori \(\zeta(2n+1)\) ci sono infiniti numeri irrazionali.
Conclusione
In questo articolo abbiamo esplorato alcune delle proprietà dei numeri reali, in base alla distinzione fra numeri razionali e numeri irrazionali.
In un prossimo articolo studieremo i numeri reali secondo un’altra suddivisione altrettanto importante: i numeri algebrici e i numeri trascendenti.
Bibliografia
[1]A. Benjamin, E. Brown – Biscuits of Number Theory (Mathematical Association of America)
[2]M. Tiles – The Philosophy of Set Theory: An Historical Introduction to Cantor’s Paradise (Dover)
[3]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers (Wiley)
[4]Hardy, Wright – An introduction to the Theory of Numbers (V edition, Oxford, 1979)
[5]D. Knuth – The Art of Computer Programming: Seminumerical Algorithms (Addison-Wesley)
[6]R. Apéry – Irrationalité de zeta(2) et zeta(3) (Astérisque 61, 1979)

4 commenti
Marco · 8 Luglio 2021 alle 11:32 AM
Complimenti per i contenuti, eccellente esposizione!
Ho un po’ di difficoltà a capire come la zeta di Rieman si annulli negli interi pari negativi. Conosco la rappresentazione funzionale della zeta tramite la funzione gamma e il sin(s*pi/2) ma il fatto che per s=-2, per esempio, la somma di tutti i quadrati dia come risultato 0 è qualcosa che ho difficoltà a comprendere. Analogamente come la zeta valutata in -1, ovvero la somma di tutti i numeri naturali, sia un valore finito, razionale e addirittura negativo, -1/12.
Ma questo esula dai contenuti del sito che sono davvero notevoli ed interessantissimi.
gameludere · 15 Luglio 2021 alle 2:58 PM
Ciao Marco! Grazie mille per il commento e scusa per la risposta un po’ tardiva.
Aggiungo alcune note per chiarire i tuoi dubbi sul calcolo dei valori della funzione zeta.
L’espressione \(\zeta(s)= \sum\limits_{n=1}^{\infty}\dfrac{1}{n^{s}}\), con \(s=\sigma + it\), definisce la funzione zeta nella regione piana a destra della retta \(\sigma=1\), dove la serie converge. Tuttavia la serie non può essere utilizzata per calcolare i valori della \(\zeta(s)\) fuori dal suo dominio di convergenza, ad esempio nel punto \(s=-2\). Bisogna infatti distinguere tra una funzione e le sue diverse rappresentazioni parziali che può avere. La serie di Dirichlet \(\sum\limits_{n=1}^{\infty}\dfrac{1}{n^{s}}\) è una rappresentazione parziale della \(\zeta(s)\), valida solo in una parte del dominio di definizione della funzione. Infatti la \(\zeta(s)\) è una funzione definita in tutto il piano complesso, ad eccezione del punto \(s=1\), dove ha una singolarità, un polo semplice dove il modulo diventa infinito. Per determinare i valori nella regione \(\sigma \le 1\) bisogna utilizzare altre rappresentazioni della stessa funzione zeta, valide anche in questa regione, ottenute mediante la teoria della continuazione analitica delle funzioni di variabile complessa.
Per determinare gli zeri banali della funzione zeta a sinistra della striscia critica \(0 \le \sigma \le 1\), si può utilizzare direttamente l’equazione funzionale \(\zeta(s)=2(2\pi)^{s-1} \sin(\frac{1}{2}\pi s)\Gamma(1-s)\zeta(1-s)\), valida per tutti i valori di \(s\).
La funzione \(\zeta(s)\) non ha zeri nella regione \(\sigma \ge 1\) e ha soltanto un polo in \(s=1\). La funzione \(\Gamma(s)\) non ha zeri e diventa infinita nei poli \(\{s=0,-1,-2,\cdots\}\). Quindi la funzione \(\Gamma(1-s)\) ha poli in \(\{1-s=0,-1,-2, \cdots\}\), cioè in \(\{s=1,2,3,\cdots\}\). I poli di \(\Gamma(1-s)\) nei valori dispari \(\{1-s=-1,-3,-5,\cdots\}\) sono cancellati dagli zeri di \(\sin \frac{1}{2}\pi s\), mentre i poli nei valori pari \(\{1-s=-2,-4,-6,\cdots\}\) sono cancellati dagli zeri banali di \(\zeta(1-s)\).
Un consiglio finale. La funzione zeta è una delle funzioni più belle e importanti della matematica, con applicazioni anche nel campo della fisica. Tuttavia per comprendere le sue proprietà è indispensabile studiare in modo approfondito la teoria delle funzioni di una variabile complessa.
Marco Marino · 15 Luglio 2021 alle 4:20 PM
Nessun problema, ci mancherebbe. Spiegazione chiarissima. Argomento interessantissimo da approfondire. Consigli questo testo S. Lang – Complex Analysis per lo scopo?
sull’utilizzo della serie per calcolare i valori negli inetri negativi avevo notato che in alcuni contesti di meccanica quantistica si usava a volte come somma della serie \(\zeta(s)= \sum\limits_{n=1}^{\infty}\dfrac{1}{n^{s}} -1/12\) per questo credevo che si potesse usare la definizione della Zeta function anche negli interi negativi.
Grazie mille per l’ottima spiegazione.
Marco
gameludere · 16 Luglio 2021 alle 11:36 AM
Per quanto riguarda la formula che hai riportato bisognerebbe capire in che contesto viene utilizzata. Sappiamo che \(\zeta(-1)=-\frac{1}{12}\). Comunque la serie non converge per \(\sigma \le 1\).
Esistono ottimi testi di analisi complessa. La cosa importante oltre allo studio della teoria è fare molti esercizi. Lang è sicuramente un autore importante e su internet si possono trovare le soluzioni ai suoi esercizi. Altri libri buoni secondo la mia esperienza sono:
1. Spiegel – Complex analysis (Schaum) (numerosi esercizi svolti)
2. Freitag – Complex analysis (Springer)
Una volta acquisita una buona conoscenza dell’analisi complessa si può iniziare lo studio della teoria analitica dei numeri e in particolare della funzione zeta di Riemann. Per questi posso consigliare i seguenti libri:
1. Apostol – Introduction to analytic number theory (Springer)
2. Titchmarsh – The Theory of Riemann Zeta Function (Oxford) (un classico)
3. Edwards – Riemann Zeta Function (Dover)
I libri di Titchmarsh e Edwards contengono i principali risultati riguardanti la funzione zeta, la distribuzione dei numeri primi e l’ipotesi di Riemann.