I principali insiemi numerici utilizzati in matematica sono i seguenti:
- \(\mathbb{N} =\{0,1,2,3,\cdots\} \quad \text{ (numeri naturali o interi non negativi)}\)
- \(\mathbb{Z} =\{\cdots,-3,-2,-1,0,1,2,3,\cdots\} \quad\text{(numeri interi)} \)
- \(\mathbb{Q} =\left \{\dfrac{n}{m}, \text{con } n,m\in \mathbb{Z}, m\neq 0\right\} \quad \text{(numeri razionali)}\)
- \(\mathbb{R} =\text{(numeri reali)}\)
- \(\mathbb{C} =\text{(numeri complessi)}\)
Indicheremo con \(\mathbb{Z}^{+}=\{1,2,3,\cdots\}\) l’insieme degli interi positivi. Alcuni autori non includono lo zero nell’insieme dei numeri naturali e quindi indicano con \(\mathbb{N}\) l’insieme degli interi positivi. Notiamo che
\[ \mathbb{N}\subset\mathbb{Z} \subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C} \]I numeri reali possono rappresentare grandezze geometriche continue, come la distanza fra due punti su una retta, o l’area di una figura geometrica piana. Il sistema dei numeri reali, pur essendo completo dal punto di vista della continuità, ha dei limiti dal punto di vista algebrico. Ad esempio l’equazione \(x^{2}+1=0\) non ha soluzione nel campo dei numeri reali. L’incompletezza algebrica del sistema dei numeri reali ha portato ad ampliare il sistema dei numeri aggiungendo i numeri complessi. Questi nuovi oggetti sono stati inizialmente guardati con riserva da molti matematici. Tuttavia, gradualmente sono stati definiti in modo rigoroso e si sono rivelati fondamentali per gli sviluppi della matematica, e hanno trovato applicazioni anche nella fisica matematica.
In questo articolo descriveremo le principali fasi della scoperta dei numeri complessi e studieremo le loro principali proprietà.
1) Breve storia dei numeri complessi
“Ex irrationalibus oriuntur quantitates impossibiles seu imaginariae, quarum mira est natura, et tamen non contemnenda utilitas”
G. W. Leibniz (1646-1716)
[Dagli irrazionali nascono le quantità impossibili o immaginarie, delle quali è stupefacente la natura, ma la cui utilità, tuttavia, non è da disprezzare.]
1.1) Il problema di Erone di Alessandria
La presenza di soluzioni complesse nei problemi matematici può essere fatta risalire al primo secolo dopo Cristo, quando il matematico Erone di Alessandria cercava di calcolare il volume di un tronco di piramide con base quadrata. Il problema è incluso nel suo libro ‘Stereometria’: dato un tronco di piramide con la lunghezza del lato del quadrato della base maggiore uguale ad \(a\), la lunghezza dei lati del quadrato della base minore uguale a \(b\), e la lunghezza dei segmenti che congiungono i vertici delle due basi uguale a \(c\), determinare l’altezza del tronco (frustum).
Erone trovò la seguente formula per l’altezza \(h\):
\[ h =\sqrt{c^{2}- \frac{(a-b)^2}{2}} \]La formula si dimostra facilmente mediante il teorema di Pitagora.
Supponendo \(a=10,b=2,c=9\) la formula da il valore corretto \(h=7\). Tuttavia non sempre la formula funziona. Erone ad esempio prese questi valori: \(a=28,b=4 , c=15\) e ottenne il seguente risultato:
Erone registrò il risultato nella forma \(\sqrt{63}\). Spiegò il risultato con il fatto che nella realtà non può esistere un frustum con queste tre dimensioni, così come non esiste un triangolo con i lati \((3,4,10\)). Probabilmente fu uno dei primi casi in cui nella soluzione di un problema geometrico si presentarono radici quadrate di numeri negativi. Tuttavia i tempi non erano maturi: bisognerà aspettare circa \(1500\) anni prima che venga accettata l’idea di fare operazioni con radici quadrate di numeri negativi. L’introduzione dei numeri complessi o immaginari venne fatta nel periodo del Rinascimento per risolvere le equazioni algebriche di grado superiore al primo.
1.2) Le equazioni di secondo grado
L’equazione di secondo grado \(ax^{2}+bx + c = 0\) non ha soluzioni positive se \(a,b,c \gt 0\). I Babilonesi furono i primi a risolvere problemi di geometria che portavano ad equazioni dei secondo grado. Ad esempio, determinare le dimensioni \(x,y\) di un rettangolo, conoscendo il perimetro \(2p\) e l’area \(A\):
\[ \begin{array}{l} x + y = p \\ x \cdot y = A \end{array} \]I Babilonesi risolvevano le equazioni con metodi geometrici, poiché non avevano ancora il concetto di equazione algebrica. Il metodo dei babilonesi è sostanzialmente equivalente al metodo del completamento del quadrato. Supponendo \(a \neq 0\) abbiamo:
\[ \begin{array}{l} x^{2}+\dfrac{b}{a}x + \dfrac{c}{a}= x^{2}+\dfrac{b}{a}x + \dfrac{b^{2}}{4a^{2}}-\dfrac{b^{2}}{4a^{2}} + \dfrac{c}{a}= \\ \left(x+\dfrac{b}{2a}\right)^2 – \dfrac{b^{2}}{4a^{2}} + \dfrac{c}{a}=0 \end{array} \]Risolvendo l’ultima equazione calcolando le due radici quadrate, troviamo le due soluzioni
\[ x_{1}=\frac{-b + \sqrt{b^{2}-4ac}}{2a} \quad x_{2}=\frac{-b – \sqrt{b^{2}-4ac}}{2a} \quad \]Naturalmente, se la quantità \(\Delta=b^{2}-4ac\) è negativa non ci sono soluzioni reali. In realtà i Babilonesi considerarono solo equazioni particolari: \(x^{2}+bx -c=0\) e \(x^{2}-bx -c =0\). In questi casi si ottengono radici quadrate di numeri positivi, e non si presenta il problema delle radici di numeri negativi.
Importanti progressi nell’algebra vennero ottenuti dal matematico indiano Brahmagupta (598-665 d.C.). Egli per primo introdusse lo zero nelle operazioni aritmetiche, definito come il risultato della differenza di un numero con se stesso. Formulò anche le regole per effettuare calcoli con i numeri negativi. Brahmagupta diede anche la formula generale dell’equazione di secondo grado, considerando le due radici anche nel caso che una di esse fosse negativa. Brahmagupta fu uno dei primi matematici a considerare i numeri in modo astratto, senza collegarli necessariamente a operazioni pratiche, come il conteggio di oggetti o la misura di lunghezze. In questo senso è uno dei precursori della visione moderna della matematica, come scienza basata su simboli e operazioni logiche.
Il matematico arabo Al-Khwarizmi (780-850) publicò diverse soluzioni di equazioni di secondo grado nella sua opera ‘Algebra’. Tuttavia, si limitò a trattare casi in cui i coefficienti e le soluzioni sono positivi.
1.3) I matematici del Rinascimento e le equazioni algebriche di terzo e quarto grado
Le formule risolutive per le equazioni di terzo e quarto grado vennero trovate nella prima metà del secondo XVI. I matematici protagonisti erano italiani: Scipione del Ferro, Ludovico Ferrari, Tartaglia, Gerolamo Cardano, ed altri. Questi matematici furono tra i primi a fare calcoli anche con le radici di numeri negativi. Quando si presentava una radice quadrata di un numero negativo, si parlava di “caso irriducibile”, e le soluzioni venivano scartate, in quanto ritenute impossibili.
L’equazione generale di terzo grado può essere scritta nel modo seguente:
Scipione del Ferro (1455-1526) diede la formula generale per le equazioni di terzo grado del seguente tipo
\[ x^{3}+px = q \ , \quad p,q \gt 0 \]Prima della morte nel 1526 rivelò la formula ad un suo studente, Antonio Maria Fior. Il matematico Nicolò Fontana (1499 circa,1557), chiamato Nicolò Tartaglia per sue balbuzie, riuscì a ricavare un metodo per risolvere le equazioni di terzo grado ridotte, cioè senza il termine di secondo grado:
\[ x^{3}+bx+c=0 \]Gerolamo Cardano (1501-1576) riuscì a farsi rivelare la formula da Tartaglia, con la promessa di mantenerla segreta.
Nel 1545 Cardano pubblicò in Germania la sua importante opera ‘Ars Magna’. La pubblicazione di questo libro per molti rappresenta l’inizio della matematica moderna. Nel libro Cardano presentò tra l’altro le soluzioni delle equazioni generali di terzo e quarto grado, e anche il modo di passare dall’equazione generale a quella ridotta. In realtà Cardano generalizzò la formula di Tartaglia, introducendo le radici di numeri negativi. Il fatto di aver pubblicato la formula di Tartaglia nella sua opera fece scatenare una contesa fra i due matematici. Tuttavia erano passati diversi anni dalla promessa fatta a Tartaglia e ,durante questo periodo, Tartaglia non aveva mai voluto pubblicare la sua formula.
Insieme a Cardano, Tartaglia e Scipione del Ferro va ricordato anche un altro matematico, Ludovico Ferrari (1522-1565), allievo di Cardano, che scoprì la formula per le equazioni di quarto grado.
Cardano considerò questi tre tipi di equazioni:
Non considerò l’equazione generale \(x^{3}+bx+c=0\), poiché venivano trattati solo numeri positivi, quindi l’equazione non ammette soluzioni.
La formula generale data da Cardano per risolvere l’equazione ridotta di terzo grado è la seguente:
Esercizio 1.1
Calcolare le soluzioni dell’equazione \(x^{3}=6x+6\).
Nonostante l’importanza della formula ottenuta, rimaneva comunque da risolvere un problema fondamentale: non si riusciva a trattare il cosiddetto caso irriducibile, cioè quando \(\dfrac{c^{2}}{4} + \dfrac{b^{3}}{27} <0\).
Se la grandezza nelle radici quadrate era negativa allora ci si trovava in presenza dei cosiddetti numeri immaginari, che ancora non erano stati introdotti nella matematica.
Il termine numero immaginario venne introdotto da Cartesio (1596-1650). Cartesio considerava vere solo le soluzioni reali positive, mentre considerava false le radici immaginarie, così come le reali negative.
1.4) Raffaele Bombelli
Pur non esistendo ancora una definizione formale e una teoria rigorosa dei numeri complessi, il matematico italiano Raffaele Bombelli (1526-1572) riuscì a definire delle regole di calcolo con i numeri immaginari, che permisero di comprendere meglio anche le soluzioni delle equazioni nei casi irriducibili. Nel \(1572\) pubblicò la sua opera ‘Algebra’, nella quale tra l’altro sono esposte per la prima volta le regole per effettuare calcoli con le radici di numeri negativi. Bombelli utilizza la notazione \(\sqrt{-1}\) e la chiama “più di meno”. Quindi definisce le seguenti regole:
“Più via più di meno, fa più di meno. Meno via più di meno, fa meno di meno. Più via meno di meno, fa meno di meno. Meno via meno di meno, fa più di meno. Più di meno via più di meno, fa meno. Più di meno via men di meno, fa più. Meno di meno via più di meno, fa più. Meno di meno via men di meno, fa meno”
Introducendo il simbolo \(i=\sqrt{-1}\) le regole di Bombelli sono riassunte nella seguente tabella di Cayley:
\[ \begin{array}{r|rrrr} \times\quad & 1\ &\ i\ &\ -1\ &\ -i\\ \hline 1\quad &\ 1\ &\ 1\ &\ -1\ &\ -i\ \\ i\quad &\ 1\ &\ -1\ &\ -i\ &\ 1\ \\ -1\quad &\ -1 \ &\ -i\ &\ 1\ &\ i\ \\ -i\quad &\ -i\ &\ 1\ &\ i\ &\ -1\ \end{array} \]Bombelli in particolare studiò la seguente equazione
\[ x^{3}=15x+4 \]Si vede facilmente che una soluzione è \(x=4\). Applicando la formula di Cardano si trovano le seguenti soluzioni
\[ x= \sqrt[3]{2+ \sqrt{-121}}+ \sqrt[3]{2- \sqrt{-121}} \]L’idea di Bombelli è di ricavare la soluzione \(x=4\) a partire dalle soluzioni date dalla formula. Poniamo
\[ \sqrt[3]{2+ \sqrt{-121}}= a+ b\sqrt{-1} \]Applicando le sue regole si ha
\[ \sqrt[3]{2- \sqrt{-121}}= a- b\sqrt{-1} \]Con semplici passaggi algebrici si trova che \(a=2,b=1\) e quindi la soluzione
\[ x = a+bi + a-bi = 2a = 4 \]Quindi, attraverso l’utilizzo dei numeri immaginari Bombelli riesce a ritrovare la soluzione reale.
Esercizio 1.2
Mediante la formula di Cardano trovare le tre radici reali dell’equazione
Soluzione: ([4,2+\sqrt{3},2-\sqrt{3}])
Esercizio 1.3
Mediante le regole di Bombelli, dimostrare la seguente identità:
1.5) Gli sviluppi successivi
Nel periodo successivo molti matematici, tra i quali Leibniz, Newton, Eulero e Gauss, utilizzarono frequentemente i numeri complessi, pur senza avere ancora definito in modo rigoroso il loro significato. Un’idea comune era quella di considerare le soluzioni complesse come indicazione dell’impossibilità del problema.
Eulero (1707-1783) pubblicò nel \(1748\) la sua opera fondamentale ‘Introductio in Analysin infinitorum’, che può essere considerata la base dell’analisi matematica moderna. Oggetto principale era lo studio delle funzioni e delle loro proprietà. Eulero introdusse il simbolo \(i\) per rappresentare la radice quadrata \(\sqrt{-1}\). Nella sua opera Eulero introdusse alcune formule fondamentali relative ai numeri complessi, tra le quali la seguente:
Come caso particolare abbiamo la famosa formula
\[ e^{i \pi } = -1 \]Verso la fine del secolo XVIII l’utilizzo dei numeri complessi nella forma cartesiana \(x+iy\) diventò comune fra i matematici. Gauss introdusse il termine numeri complessi nel \(1832\) e ne diede una interpretazione geometrica. Un numero complesso \(z=x+iy\) veniva rappresentato come un punto del piano, di coordinate cartesiane reali \((x,y)\).
Nel \(1799\) Gauss pubblicò la prima dimostrazione del seguente teorema:
Teorema fondamentale dell’algebra
Un’equazione di grado \(n\) ha sempre esattamente \(n\) soluzioni nel campo dei numeri complessi.
Si tratta di un risultato fondamentale per l’algebra, che convinse i matematici ad accettare definitivamente i nuovi numeri.
Una definizione rigorosa dei numeri complessi venne data da William Rowan Hamilton (1805-1865). Hamilton considerò un numero complesso come una coppia di numeri reali, e definì le operazioni di addizione e moltiplicazione in modo che siano rispettate le proprietà commutativa, associativa e distributiva.
Ricordiamo che Hamilton creò anche una nuova tipologia di numeri, i quaternioni, che estendono i numeri complessi. I quaternioni soddisfano tutte le proprietà algebriche dei numeri complessi, tranne la proprietà commutativa dell moltiplicazione. Per una introduzione ai quaternioni e alle loro applicazioni vedere l’articolo su questo sito.
Per la storia dell’algebra vedere il testo di Van der Waerden[1].
2) La definizione moderna dei numeri complessi
La definizione moderna dei numeri complessi è sostanzialmente analoga a quella di Hamilton. L’insieme dei numeri complessi \(\mathbb{C}\) è costituito da tutte le coppie di numeri reali. Quindi
\[ \mathbb{C}=\mathbb{R}\times \mathbb{R}= \{(x,y) : x,y \in \mathbb{R}\} \]Un numero complesso può essere rappresentato con la notazione \(z=(x,y)\), dove \(x\) è la parte reale e \(y\) la parte immaginaria. Si usa anche la notazione \(x=\Re(z)\) e \(y=\Im(z)\).
Un numero complesso \(z=(0,y)\), con \(y \neq 0\), viene chiamato immaginario puro. Il coniugato di \(z=(a,b)\) è il numero complesso \(\overline{z}=(a,-b)\).
Operazioni di addizione e moltiplicazione
Per ogni coppia di numeri complessi \(z=(x_{1},y_{1}),w=(x_{2},y_{2})\) definiamo le operazioni di addizione e moltiplicazione:
È facile verificare che con le due operazioni l’insieme dei numeri complessi è un campo algebrico. Infatti \(\mathbb{C}\) è un gruppo abeliano con l’operazione di addizione, mentre \(\mathbb{C}{\setminus}{0}\) è un gruppo abeliano con l’operazione di moltiplicazione. Inoltre, dati \(3\) numeri complessi \(z_{1},z_{2},z_{3}\), vale la proprietà distributiva:
\[ \begin{array}{l} z_{1}(z_{2}+z_{3}) = z_{1}z_{2} + z_{1}z_{3} \end{array} \]
L’inverso additivo del numero complesso \(z=(a,b)\) è \(-z=-(a,b)=(-a,-b)\). L’inverso moltiplicativo del numero complesso \(z=(a,b)\) con \(b \neq 0\) è
Operazioni di sottrazione e divisione
Dati due numeri complessi \(z,w\), le operazioni di sottrazione e divisione sono così definite:
I numeri reali sono un sottoinsieme dei numeri complessi. Infatti un numero complesso con parte immaginaria nulla, cioè \(z=(a,0)\), può essere identificato con il numero reale \(a\).
Esercizio 2.1
Definiamo la funzione \( z \to \overline{z}\), chiamata la riflessione sull’asse reale. Dimostrare che questa funzione è un automorfismo di \(\mathbb{C}\), cioè che valgono le seguenti formule
Esercizio 2.2
Dimostrare che il prodotto di un numero complesso non nullo per il suo coniugato è un numero reale positivo.
Dimostrare che il quadrato di un numero immaginario puro è un numero reale negativo.
2.1) Rappresentazione cartesiana
Il numero complesso \(z=(0,1)\) ha un ruolo particolare e viene indicato con il simbolo \(i\). Viene chiamato unità immaginaria, in quanto
\[ i^{2}=(0,1)\cdot (0,1)=(-1,0)=-1 \]In generale, per ogni intero positivo \(n\) si ha
\[ i^{4n}=1, \quad i^{4n+1}=i, \quad i^{4n+2}=-1, \quad i^{4n+3}=-i \]Esercizio 2.3
Verificare che
Le relazioni precedenti permettono di scrivere un numero complesso \(z=(a,b)\) nella seguente forma alternativa:
\[ \begin{array}{l} z=(a,b)=(a,0) + (0,b)= (a,0)+(b,0)\cdot (0,1) = a+ib \end{array} \]Esercizio 2.4
Siano dati due numeri complessi \(z_{1}=x_{1}+iy_{1}\) e \(z_{2}=x_{2}+iy_{2}\). Dimostrare che
Esercizio 2.5 – Disuguaglianza triangolare
Dati due numeri complessi \(z_{1},z_{2}\), dimostrare le seguenti disuguaglianze:
Suggerimento
Ricordare le proprietà dei lati di un triangolo. Inoltre, osservare che vale la formula
Dimostrare anche che vale il segno di uguaglianza se e solo se \(\dfrac{z_{1}}{z_{2}} \ge 0\), con \(z_{2} \neq 0\).
Esercizio 2.6
Trovare le soluzioni complesse dell’equazione \(z^{2}+z+4=0\), risolvendo il sistema costituito dalla parte reale e dalla parte immaginaria.
Soluzione: \(z=\left(-\frac{1}{2} \pm i\frac{\sqrt{15}}{2}\right)\).
2.2) Rappresentazione trigonometrica
Un numero complesso può essere rappresentato come un punto del piano, o in modo equivalente con un vettore che collega l’origine del sistema di assi cartesiani e il punto stesso. Consideriamo la seguente figura, chiamata anche diagramma di Gauss-Argand:
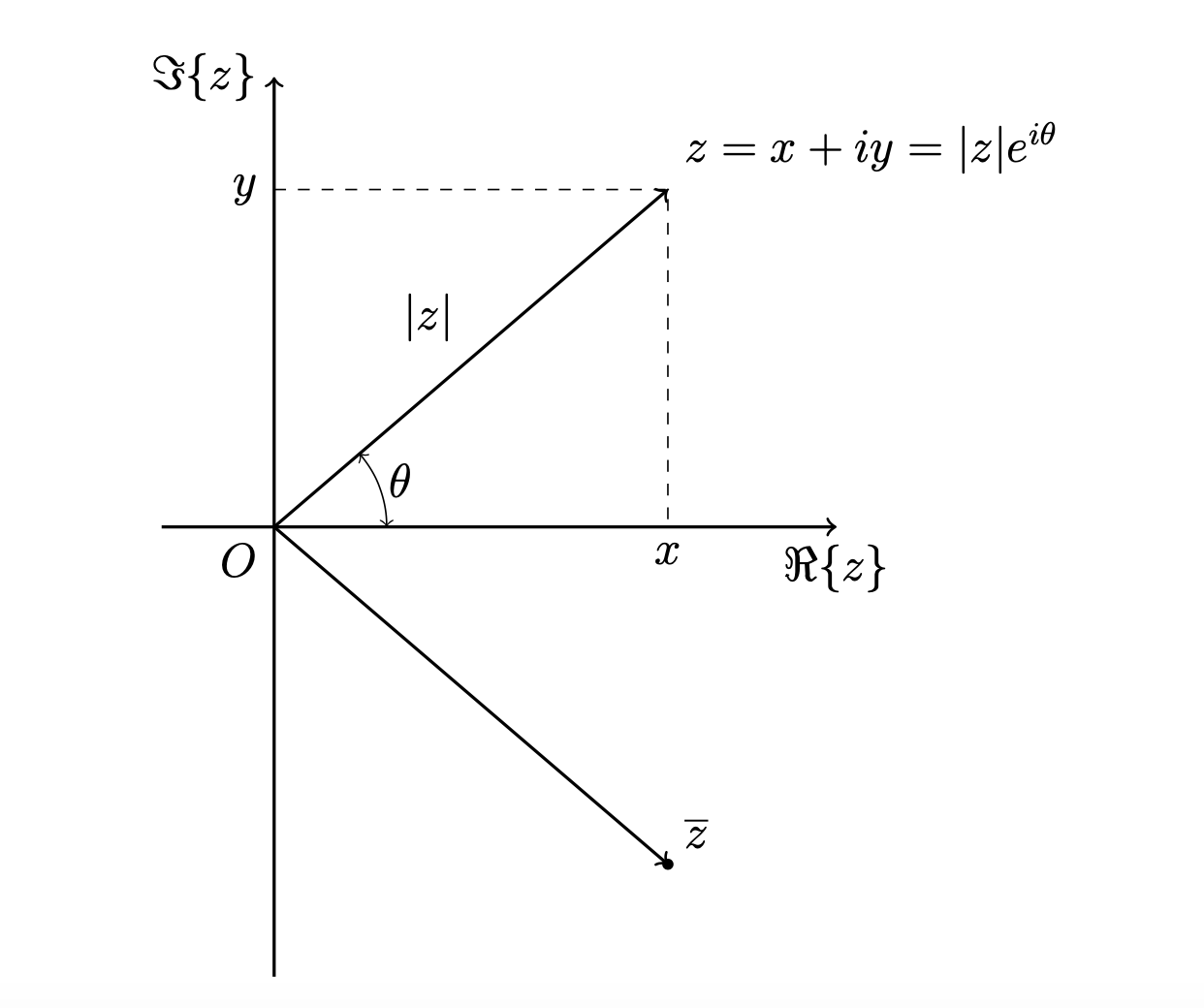
L’angolo orientato \(\theta\) fra l’asse delle \(x\) e il vettore corrispondente al numero complesso viene considerato positivo se ottenuto con una rotazione antioraria. Dal diagramma otteniamo la seguente rappresentazione trigonometrica o polare del numero complesso \(z\):
\[ \begin{array}{l} x = r \cos \theta \\ y = r \sin \theta \\ z= x+iy=r \cos \theta + i r \sin \theta \end{array} \]Il numero reale \(|z|=\sqrt{z \overline{z}}=\sqrt{x^{2}+y^{2}}\) si chiama modulo o valore assoluto di \(z\), mentre l’angolo \(\theta\) si chiama argomento di \(z\), indicato con \(\text{arg } z\).
La somma di due numeri complessi equivale alla somma di due vettori, con la nota regola del parallelogramma. La somma corrisponde alla diagonale del parallelogramma costruito a partire dai due numeri complessi.
Esercizio 2.7
Esprimere i seguenti numeri complessi in forma trigonometrica:
L’argomento può assumere un valore reale qualsiasi; i valori negativi e positivi corrispondono rispettivamente ad angoli misurati in senso orario o antiorario. L’argomento di \(z\) quindi può assumere infiniti valori, che differiscono tra loro per \(2k\pi\), dove \(k\) è un intero.
Due numeri complessi sono uguali se hanno lo stesso modulo e se i loro argomenti differiscono di un multiplo di \(2\pi\). Per ogni numero complesso \(z \neq 0\), esiste un unico valore dell’argomento \(\theta\) nell’intervallo \( 0 \le \theta < 2\pi\).
Si può prendere qualunque intervallo di lunghezza \(2\pi\).
Nel seguito utilizzeremo l’intervallo \( -\pi < \theta \le \pi\). In questo modo il valore dell’argomento è continuo sul semiasse reale positivo, mentre ha una discontinuità sul semiasse reale negativo. Il valore di \(\theta\) così scelto si chiama valore principale e si indica con \(\text{Arg } z\). In termini formali possiamo scrivere
Alcuni autori utilizzano l’intervallo \(0 \le \theta \lt 2\pi\) per definire il valore principale.
Esercizio 2.8
Dimostrare la seguente formula
Esempio 2.1
Il numero \(z=1+i\) in forma trigonometrica è
Notiamo che uno qualunque dei valori \(\theta = \dfrac{\pi}{4} + 2k\pi\), con \(k \in \mathbb{Z}\), può essere usato.
Il numero \(z=1-i\) in forma trigonometrica è
Esercizio 2.9
Calcolare l’argomento principale del numero complesso \(z=\dfrac{-2}{1+i\sqrt{3}}\).
Risposta: \(\left[\text{Arg z} = \dfrac{2\pi}{3}\right]\).
Esercizio 2.10
Siano dati due numeri complessi \(z_{1}=r_{1}(\cos \theta_{1}+ i \sin \theta_{1})\) e \(z_{2}=r_{2}(\cos \theta_{2}+ i \sin \theta_{2})\). Dimostrare le seguenti proprietà della funzione a più valori \(\arg z\):
Le identità sopra riportate vanno interpretate come uguaglianze fra due insiemi, cioè gli elementi dell’insieme alla sinistra sono uguali agli elementi dell’insieme alla destra delle identità. Non devono essere considerate come uguaglianze fra numeri.
Esercizio 2.11
Dati \(z_{1}=r_{1}(\cos \theta_{1}+ i \sin \theta_{1})\) e \(z_{2}=r_{2}(\cos \theta_{2}+ i \sin \theta_{2})\), dimostrare le seguenti formule:
Suggerimento
Ricordare le formule di addizione e sottrazione della trigonometria. Ad esempio \(\cos(\alpha + \beta)= \cos \alpha \cos \beta -\sin \alpha \sin \beta\).
Esercizio 2.12 – Formula binomiale
Dati due numeri complessi \(z,w\) e un intero positivo \(n\) dimostrare la seguente formula:
Ricordiamo che \(\displaystyle\binom{n}{k}=\dfrac{n!}{k!(n-k)!}\) e \(0!=1\).
Teorema 2.1 – Formula di de Moivre (1667 – 1754)
Dato \(n\) un intero positivo, vale la seguente formula
Dimostrazione
Dimostriamo prima la formula per gli interi non negativi, mediante il metodo di induzione. La formula è certamente vera per \(n=0,1\). Supposta vera per un valore intero non negativo qualsiasi, si deve dimostare che vale anche per \(n+1\), cioè
Moltiplicando per \((\cos \theta + i \sin \theta)\) abbiamo
\[ \begin{array}{l} (\cos \theta + i \sin \theta)^{n+1}= (\cos n\theta + i\sin n\theta) (\cos \theta + i\sin \theta)= \\ (\cos n\theta \cos \theta -\sin n\theta \sin \theta) + i( \cos n\theta \sin \theta + \sin n\theta \cos \theta) \end{array} \]Utilizzando le formule trigonometriche di addizione per le funzioni seno e coseno otteniamo la formula di de Moivre. Per dimostrare la formula per gli interi negativi ricordare che la funzione seno è una funzione dispari, mentre il coseno è una funzione pari, cioè: \(\sin (-x) = -\sin x\) e \(\cos (-x)= \cos x\).
Esercizio 2.13
Calcolare \((1+i)^{1000}\).
Risposta: \([2^{500}]\)
Esercizio 2.14
Dimostrare le seguenti identità trigonometriche:
2.3) Rappresentazione esponenziale
Eulero, nella sua opera ‘Introductio in Analysin infinitorum’, ha pubblicato la seguente formula che lega alcune delle principali costanti della matematica:
\[ e^{i\pi}+1 =0 \]Questa formula è un caso particolare della seguente formula più generale scoperta da Eulero:
\[ e^{i\theta}=\cos \theta + i \sin \theta \]Per comprendere la formula di Eulero ricordiamo gli sviluppi in serie di Taylor delle seguenti funzioni, considerate nel campo reale:
\[ \begin{array}{l} e^{x}=\sum\limits_{n=0}^{\infty}\dfrac{x^{n}}{n!}=1 + x + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} + \dfrac{x^{4}}{4!} + \cdots \\ \sin x =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{x^{2n+1}}{(2n+1)!}= x – \dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} -\cdots \\ \cos x =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{x^{2n}}{(2n)!}=1 – \dfrac{x^{2}}{2!} + \dfrac{x^{4}}{4!} -\cdots \\ \end{array} \]Possiamo definire serie analoghe sostituendo la variabile complessa \(z=x+iy\) al posto della variabile reale \(x\):
\[ \begin{array}{l} e^{z}=\sum\limits_{n=0}^{\infty}\dfrac{z^{n}}{n!} \\ \\ \sin z =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{z^{2n+1}}{(2n+1)!} \\ \\ \cos z =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{z^{2n}}{(2n)!} \\ \end{array} \]Si tratta di funzioni di variabile complessa, che ad ogni punto del piano complesso associano un numero complesso.
In articoli successivi studieremo le proprietà delle funzioni di variabile complessa e in particolare lo sviluppo in serie di Taylor, analogo a quello delle funzioni reali di variabili reali. In particolare dimostreremo che le nuove funzioni trigonometriche sono ben definite nel piano complesso e le serie di Taylor convergono su tutto il piano complesso.
La convergenza su tutto il piano complesso della funzione esponenziale segue facilmente dalla seguente disuguaglianza:
A questo punto per dimostrare la formula di Eulero mettiamo il valore \(z=ix\) nello sviluppo della funzione \(e^{z}\):
\[ \begin{array}{l} e^{ix}=1 + ix + \dfrac{(ix)^{2}}{2!} + \dfrac{(ix)^{3}}{3!} + \dfrac{(ix)^{4}}{4!} + \cdots = \\ \\1 + ix -\dfrac{x^{2}}{2!} -i\dfrac{x^{3}}{3!} + \dfrac{x^{4}}{4!} + \cdots = \\ \\
\left(1 -\dfrac{x^{2}}{2!} + \dfrac{x^{4}}{4!} -\cdots \right) + i \left(x -\dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} + \cdots \right) = \\ \cos x + i \sin x \end{array} \]
Eulero nella sua opera ha espresso la sua formula limitatamente al caso \(x\) reale. Tuttavia la formula è valida anche nel caso complesso: \(e^{iz}=\cos z + i \sin z\). Dalla formula di Eulero segue subito che \(e^{2\pi i}=1\) e \(e^{-\pi i }=-1\).
Mediante la formula di Eulero un numero complesso può quindi essere rappresentato in questo modo:
La forma esponenziale è utile in alcune operazioni con i numeri complessi, ad esempio nella moltiplicazione:
\[ z_{1}z_{2}=r_{1}e^{i\theta_{1}}r_{2}e^{i\theta_{2}} = r_{1}r_{2}e^{i(\theta_{1}+ \theta_{2})} \]Quindi per moltiplicare due numeri complessi basta fare il prodotto dei moduli e sommare gli angoli.
Per calcolare l’inverso di un numero complesso basta cambiare segno all’angolo e prendere l’inverso del modulo:
Per la divisione abbiamo:
\[ \dfrac{z_{1}}{z_{2}}=\dfrac{ r_{1}}{r_{2}}e^{i(\theta_{1}- \theta_{2})} \]Infine con la rappresentazione esponenziale la formula di de Moivre segue immediatamente:
\[ z^{n}=r^{n}e^{i n\theta}=r^{n}(\cos n\theta + i \sin n\theta) \]Ricordiamo che la funzione esponenziale spesso viene indicata anche con la notazione \(\exp(z)=e^{z}\).
3) Le radici di un numero complesso
Sia \(n\) un intero positivo. Un numero complesso \(w=\rho (\cos \phi + i \sin \phi)\) si dice radice n-esima di un numero complesso \(z= r (\cos \theta + i \sin \theta)\) se risulta \(z=w^{n}\). Il problema consiste nel determinare tutti i numeri complessi \(w\), la cui potenza ennesima dà come valore il numero complesso \(z\). Per la formula di De Moivre deve essere
\[ \rho^{n}(\cos n\phi + i \sin n\phi)= r(\cos \theta + i \sin \theta) \]Questa uguaglianza è verificata se e solo se risulta
\[ \begin{cases} \rho^{n}= r \\ \phi =\dfrac{ \theta + 2k\pi}{n} \ , \quad k=0,\pm 1,\pm2, \cdots \end{cases} \]A prima vista sembrerebbe che esistono infinite radici \(n\)-esime. Ma si vede facilmente che le radici sono distinte solo per i valori \(k=0,1,2,\cdots,n-1\). Quindi possiamo concludere che esistono \(n\) radici date dalla formula seguente:
\[ \begin{array}{l} w_{k} = \sqrt[n]{r}\left(\cos\dfrac{\theta +2k\pi}{n} + i \sin \dfrac{\theta + 2k\pi}{n}\right) \ , \quad k=0,1,\cdots, n-1 \end{array} \]Possiamo scrivere le soluzioni nella forma esponenziale:
\[ \begin{array}{l} w_{k} = \sqrt[n]{r}\exp \left(\dfrac{(\theta + 2k\pi )i}{n}\right) \ , \quad k=0,1,\cdots, n-1 \end{array} \]Esempio 3.1
Calcoliamo le radici terze del numero \(z=1+i\).
Conviene trasformare il numero nella forma trigonometrica: \(z=\sqrt{2}\left(\cos \dfrac{\pi}{4}+ i \sin \dfrac{\pi}{4}\right)\). Per la formula precedente le radici sono
Le tre radici sono i vertici di un triangolo equilatero inscritto in un cerchio, con centro nell’origine degli assi cartesiani e raggio uguale a \(\sqrt[6]{2}\). Le coordinate polari dei vertici \(A,B,C\) del triangolo equilatero sono: \(A=\left(\sqrt[6]{2};\dfrac{\pi}{12}\right), B=\left(\sqrt[6]{2};\dfrac{3\pi}{4}\right),C=\left(\sqrt[6]{2};\dfrac{17\pi}{12}\right)\).
3.1) Le radici dell’unità
Nel caso \(z=1\) le soluzioni si chiamano radici n-esime dell’unità. In base alla formula precedente le radici n-esime dell’unità sono:
\[ \epsilon_{k}=\cos \frac{2k\pi}{n}+i\sin \frac{2k\pi}{n} \ , \quad k=0,1,2,\cdots,n-1 \]Indicato \(\epsilon=\cos \dfrac{2\pi}{n}+ i \sin \dfrac{2\pi}{n}\), le radici n-esime dell’unità sono gli elementi dell’insieme
\[ U_{n}=\{\epsilon^{0}=1,\epsilon^{1},\cdots,\epsilon^{n-1}\} \]Dal punto di vista geometrico le radici n-esime dell’unità sono i vertici di un poligono regolare di \(n\) lati, inscritto nel cerchio di raggio unitario \(|z|=1\).
Esercizio 3.1 Determinare le radici quarte dell’unità.
Risposta: \(\{1;i;-1;-i\}\)
Esercizio 3.2
Determinare le radici cubiche di \(z=-8i\).
Risposta: \(\{\sqrt{3}-i; 2i;-\sqrt{3}-i\}\)
Esercizio 3.3 pag. 30
Determinare le radici quadrate di \(z=2i\) in coordinate cartesiane.
Risposta: \(\{1+i;-1-i\}\)
Esercizio 3.4
Determinare le radici quadrate, terze e seste del numero \(1\). Analizzare la relazione fra questi tre gruppi di radici.
Esercizio 3.5
Risolvere le seguenti equazioni:
Suggerimento
L’equazione \((z+1)^{2}=z^{2}\) è equivalente alla \(\left(\dfrac{z+1}{z}\right)^{2}=1\).
Esercizio 3.6
Sia \(U_{n}=\{\epsilon_{0},\epsilon_{1},\cdots,\epsilon_{n-1}\}\), l’insieme delle radici \(n\)-esime dell’unità. Dimostrare la seguente formula.
Esercizio 3.7
Sia \(\epsilon\) una radice dell’unità, con \(\epsilon \neq 1\). Dimostrare che
3.2) Le radici primitive di un numero complesso
Definizione 3.1
Una radice \(n\)-esima dell’unità si dice primitiva se
Teorema 3.1
Sia \(z= \cos \dfrac{2\pi}{n}+i \sin \dfrac{2\pi}{n}\). Se \((k,n)=d \gt 1\) allora \(z^{k}\) è una radice \(\dfrac{n}{d}\)-esima di \(1\).
Dimostrazione
Poniamo \(k=k_{1}d\) e \(n=n_{1}d\). Applicando la formula di de Moivre abbiamo
da cui segue il teorema.
Dal teorema precedente deriva il seguente teorema, che fornisce un criterio per riconoscere le radici primitive:
Teorema 3.2
Le radici primitive dell’unità sono
con \((k,n)=1\).
Esercizio 3.8
Dimostrare che se \(\epsilon \in U_{n}\) è una radice primitiva dell’unità, allora le radici dell’equazione \(z^{n}-1=0\) sono le seguenti
dove \(k\) è un intero positivo arbitrario.
4) Equazioni algebriche nel campo complesso
Ricordiamo che un polinomio nel campo complesso è una funzione \(f: \mathbb{C} \to \mathbb{C}\) della seguente forma:
\[ f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+ \cdots + a_{1}x+a_{0} \]dove i coefficienti \(a_{k}\) sono numeri complessi, con \(a_{n} \neq 0\), e \(n\) è un intero positivo chiamato il grado dell’equazione. Un polinomio con valore costante non nullo ha grado uguale a zero.
Il polinomio nullo è il polinomio i cui coefficienti sono tutti uguali a zero. Per comodità il grado del polinomio nullo viene assunto uguale a \(-\infty\).
Un polinomio si può considerare, dal punto di vista algebrico, come un’espressione formale che è definita una volta assegnati i valori dei coefficienti \(a_{k}\). In questo caso la variabile \(x\), chiamata anche indeterminata, rappresenta solo un modo di specificare la posizione dei coefficienti. Due polinomi \(p(x),q(x)\) coincidono, cioè \(p(x)=q(x)\), se e solo se hanno uguali tutti i coefficienti delle stesse potenze di \(x\).
Un polinomio può anche essere considerato dal punto di vista dell’analisi, e cioè una funzione a valori complessi della variabile complessa \(x\). In questo caso due polinomi sono uguali se i loro valori coincidono per tutti i valori di \(x\). I due punti di vista algebrico e analitico sono equivalenti.
Indichiamo con \(\mathbb{C}[x]\) l’insieme di tutti i polinomi a coefficienti complessi. Un polinomio può anche essere rappresentato da una serie infinita \(f(x)=\sum\limits_{k=0}^{\infty}a_{k}x^{k}\), con l’intesa che solo un numero finito di coefficienti è diverso da zero. Sull’insieme dei polinomi \(\mathbb{C}[x]\) possiamo definire due operazioni binarie di addizione e moltiplicazione. Dati due polinomi \(f(x) = \sum\limits_{k=0}^{\infty}a_{k}x^{k}\) e \( g(x) = \sum\limits_{k=0}^{\infty}b_{k}x^{k} \), abbiamo
Esercizio 4.1
Dimostrare che con queste operazioni \(\mathbb{C}[x]\) è un anello commutativo. Inoltre, è anche un dominio di integrità.
Per la definizione di gruppo e anello vedere l’articolo su questo sito, oppure vedere WolframMathWorld.
Ai polinomi si estendono in modo naturale i concetti di divisibilità definiti per i numeri interi. Vale l’algoritmo di divisione di Euclide, simile a quello degli interi.
Teorema 4.1 – Teorema di divisione dei polinomi
Siano dati due polinomi \(f(x),g(x) \in \mathbb{C}[x]\), con \(g(x) \neq 0\). Allora esistono e sono unici due polinomi \(q(x),r(x)\) tali che
dove \(r(x)=0\), oppure il grado di \(r(x)\) è minore del grado di \(g(x)\).
Se \(r(x)=0\) allora il polinomio \(g(x)\) si chiama divisore di \(f(x)\).
Esempio 4.1
Siano \(f(x)=3x^{3}+10x^{2}+2x-3\) e \(g(x)=x^{2}+5x+6\). Applichiamo l’algoritmo per calcolare il quoziente e il resto della divisione:
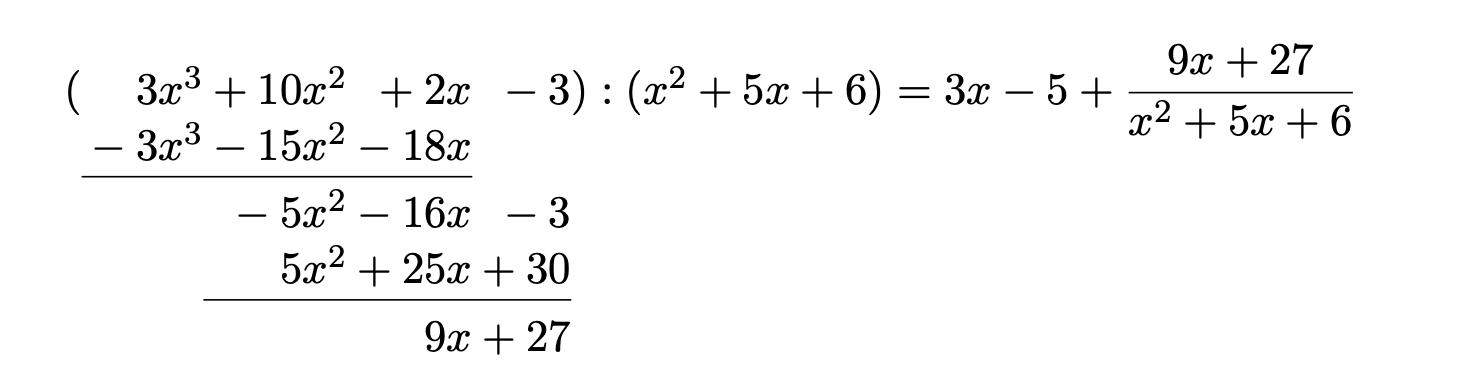
Se dividiamo un polinomio \(f(x)\) per un polinomio di primo grado, il resto è un polinomio di grado zero, cioè una costante, oppure il polinomio nullo.
Esercizio 4.2
Dimostrare che il resto della divisione del polinomio \(f(x)\) per \(x-\alpha\) è uguale al valore \(f(\alpha)\) che assume il polinomio per \(x=\alpha\).
4.1) Zeri dei polinomi
Le soluzioni dell’equazione \(f(x)=0\) sono chiamate gli zeri o radici del polinomio. Dall’esercizio precedente si ricava il seguente:
Teorema 4.2
Un numero \(\alpha\) è uno zero del polinomio \(f(x)\) se e solo se \(f(x)\) è divisibile per \(x-\alpha\), cioè se il resto della divisione è nullo. Se quindi \(\alpha\) è uno zero di un polinomio \(f(x)\) di grado \(n \gt 0\), allora risulta
dove \(g(x)\) è un polinomio di grado \(n-1\). Uno zero si dice di ordine \(k\) se risulta \(f(x)=(x-\alpha)^{k}g(x)\), dove \(g(x)\) non è divisibile per \(x-\alpha\), cioè \(g(\alpha) \neq 0\).
4.2) Il teorema fondamentale dell’algebra
Un problema fondamentale consiste nella determinazione di tutti gli zeri di un polinomio. Sappiamo che nel caso reale un polinomio di grado \(n\) può non avere zeri. Ad esempio l’equazione di secondo grado \(x^{2}+1=0\) non ha soluzioni reali. Nel campo complesso invece vale il seguente teorema fondamentale, dimostrato da Gauss nel \(1849\):
Teorema 4.3 – Teorema fondamentale dell’algebra
Ogni polinomio \(f(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+ \cdots + a_{1}z + a_{0}\) di grado \(n \ge 1\) ha almeno una radice complessa.
In termini algebrici, il teorema afferma che il campo dei numeri complessi \(\mathbb{C}\) è algebricamente chiuso.
Esistono numerose dimostrazioni del teorema. Una dimostrazione elegante utilizza il seguente teorema di Liouville relativo alle funzioni di variabile complessa:
Teorema 4.4 – Liouville
Una funzione intera e limitata di variabile complessa è una funzione costante su tutto il piano complesso.
Ricordiamo che una funzione intera è una funzione di variabile complessa che è derivabile in ogni punto del piano.
Mediante il teorema di Liouville, la dimostrazione del teorema fondamentale dell’algebra è immediata.
Supponiamo per assurdo che il polinomio \(f(z)\) di grado \(n\) non abbia nessuno zero. Allora la funzione \(F(z)=\dfrac{1}{f(z)}\) è una funzione derivabile in ogni punto del piano, quindi è una funzione intera. Inoltre la funzione \(F(z)\) è anche limitata, in quanto il valore del polinomio \(f(z)\) è dominato dal suo termine principale \(a_{n}z^{n}\), il quale cresce all’infinito in tutte le direzioni del piano complesso. Quindi la funzione \(F(z) \to 0\) quando \(z \to \infty\). Per il teorema di Liouville \(F(z)\) è costante e quindi è costante anche \(f(z)\). Naturalmente il polinomio\(f(z)\) di grado \(n \ge 1\) non è costante, quindi l’ipotesi iniziale che non ci siano zeri è non valida.
Esistono molte altre dimostrazioni del teorema fondamentale. Per una approfondita esposizione vedi [2].
Dal teorema precedente segue il seguente:
Teorema 4.5
Ogni polinomio di grado \(n\) a coefficienti complessi ha esattamente \(n\) radici, contando ogni radice con la sua molteplicità.
Dimostrazione
Sia \(\alpha\) una radice del polinomio \(f(z)\). Facciamo la divisione fra \(f(z)\) e \(z-\alpha\), applicando l’algoritmo di divisione fra polinomi. Abbiamo \(f(z)=(z-\alpha)g(z)+r(z)\), dove \(g(z)\) è un polinomio di grado \(n-1\) e \(r(z)\) è un polinomio di grado minore di \(1\), cioè una costante. Poiché \(\alpha\) è uno zero, abbiamo \(f(\alpha)=0\) e quindi il resto \(r=0\). Perciò abbiamo \(f(z)=(z-\alpha)g(z)\).
Procedendo per induzione sul polinomio \(g(z)\), il quale ha grado \(n-1\), otteniamo che il polinomio \(f(z)\) deve avere \(n\) radici, non necessariamente tutte distinte.
Possiamo quindi formulare il teorema fondamentale dell’algebra in questo modo equivalente:
Teorema 4.6
Sia \(f(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+ \cdots + a_{1}z+a_{0}\) un polinomio di grado \(n\) a coefficienti complessi.
Allora esistono \(k\) numeri complessi \(z_{1},\cdots,z_{k}\) distinti tra loro, e \(k\) interi positivi \(\mu_{1},\cdots,\mu_{k}\), con \(1 \le k \le n\), tali che \(\mu_{1}+ \cdots + \mu_{k}=n\) e il polinomio ha la seguente fattorizzazione:
I numeri interi \(\mu_{i}\) si chiamano molteplicità delle radici \(z_{i}\).
Esercizio 4.3
Dimostrare che, se i coefficienti \(a_{k}\) del polinomio \(p(z)\) sono reali, allora se \(z_{i}\) è uno zero del polinomio lo è anche il suo coniugato \(\overline{z_{i}}\).
Suggerimento
Ricordare le proprietà del coniugato di una somma o di un prodotto di numeri complessi.
Dall’esercizio precedente deriva subito il seguente teorema:
Teorema 4.7
Sia \(f(x)\) un polinomio a coefficienti reali. Allora \(f(x)\) può essere fattorizzato nel prodotto di fattori lineari corrispondenti agli zeri reali e nel prodotto di fattori quadratici corrispondenti agli zeri non reali.
Esercizio 4.4
Determinare la fattorizzazione del polinomio \(p(z)=z^{4}+64\), sapendo che una soluzione è \(z_{1}=2-2i\).
Suggerimento
Poiché i coefficienti sono reali, anche \(z_{2}=2+2i\) è soluzione. Dividere il polinomio iniziale per \(2-2i\), poi dividere il polinomio quoziente di terzo grado per \(2+2i\). Infine risolvere il polinomio quoziente di secondo grado con la formula classica.
Risposta: \([p(z)=(2+2i)(2-2i)(-2+2i)(-2-2i)]\)
Esercizio 4.5 – Formule di Viète
Siano \(z_{1},z_{2}, \cdots, z_{n}\) le radici, non necessariamente distinte, del polinomio \(f(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+ \cdots + a_{1}z+a_{0}\). Dimostrare che valgono le seguenti formule:
Suggerimento
Svolgere il prodotto \(f(z)=a_{n}(z-z_{1})\cdots (z-z_{n})\).
Esercizio 4.6
Trovare gli zeri del polinomio \(p(z)=z^{4}+5z^{2}-24\).
Soluzione
Si può procedere come nell’esercizio 4.4, se si riesce ad individuare una soluzione. In questo caso è preferibile effettuare delle manipolazioni algebriche:
Quindi gli zeri sono \(z=\pm\sqrt{3}, \pm 2i\sqrt{2}\).
Esercizio 4.7
Dimostrare che un polinomio di terzo grado, a coefficienti reali, può avere tre radici reali oppure una radice reale e due complesse coniugate.
Esercizio 4.8
\[ \begin{array}{l} \sin \dfrac{2\pi}{n} + \sin \dfrac{4\pi}{n} + \cdots + \sin \dfrac{2(n-1)\pi}{n} = 0 \\ \cos \dfrac{2\pi}{n} + \cos \dfrac{4\pi}{n} + \cdots + \cos \dfrac{2(n-1)\pi}{n} = -1 \\ \end{array} \]Suggerimento
Sommare le soluzioni dell’equazione \(z^{n}-1=0\) e separare la parte reale e la parte immaginaria.
4.3) Le equazioni di secondo grado
Consideriamo l’equazione di secondo grado \(az^{2}+bz+c=0\), con \(a \neq 0\). La formula generale di risoluzione si trova con semplici passaggi, mediante il completamento del quadrato:
\[ \begin{array}{l} z^{2}+ \dfrac{b}{a}z = -\dfrac{c}{a} \\ z^{2}+ \dfrac{b}{a}z + \left(\dfrac{b}{2a}\right)^{2}= -\dfrac{c}{a}+ \left(\dfrac{b}{2a}\right)^{2} \\ \left(z+ \dfrac{b}{2a}\right)^{2}= \dfrac{b^{2}-4ac}{4a^{2}} \\ \left(z+ \dfrac{b}{2a}\right) = \pm \dfrac{\sqrt{b^{2}-4ac}}{2a} \\ \end{array} \]La formula risolutiva generale è quindi
\[ z = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a} \]Notiamo che la formula generale esprime le soluzioni mediante un’espressione per radicali contenente i coefficienti \(a,b,c\) dell’equazione, combinati con le quattro operazioni aritmetiche.
Se il discriminante \(\Delta = b^{2}-4ac\) è negativo, allora non esistono soluzioni reali.
È facile verificare che se \(z_{1},z_{2}\) sono le due soluzioni dell’equazione \(az^{2}+bz+c=0\), con \(a \neq 0\), allora valgono le seguenti formule:
Esercizio 4.9
Dimostrare che la formula risolutiva può essere ottenuta effettuando la sostituzione \( z= w-\dfrac{b}{2a}\) e risolvere l’equazione nella variabile \(w\). Questa sostituzione elimina il termine di primo grado dell’equazione.
Un metodo alternativo per trovare la formula risolutiva è il seguente. Consideriamo l’equazione \(z^{2}+bz +c =0\), poniamo \(z=x+iy\) e scomponiamo l’equazione nella parte reale e nella parte immaginaria. Otteniamo il seguente sistema:
\[ \begin{cases} x^{2}-y^{2} + bx +c=0 \\ 2xy + by = 0 \end{cases} \]Dalla seconda equazione ricaviamo \(x=-\dfrac{b}{2}\). Sostituendo nella prima equazione otteniamo \(y=\pm \sqrt{c-\dfrac{b^{2}}{4}}\). Mettendo insieme abbiamo la formula
\[ z = -\frac{b}{2} \pm \sqrt{\frac{b^{2}}{4} – c} \]Esercizio 4.10
Risolvere l’equazione \(2z^{2}+z+1=0\).
4.4) Le equazioni di terzo grado
Consideriamo l’equazione generale di terzo grado:
\[ z^{3}+Az^{2}+Bz+C=0 \ , \quad A,B,C \in \mathbb{C} \]È utile procedere con una semplificazione dell’equazione, eliminando il termine di secondo grado (vedi esercizio 4.9), mediante la trasformazione di Tschirnhaus \(w=z + \dfrac{A}{3}\). In questo modo otteniamo la seguente equazione ridotta:
\[ z^{3}+ az + b=0 \]Proviamo a rappresentare le soluzioni come somma di due radici cubiche
\[ z = \sqrt[3]{p}+ \sqrt[3]{q} \]dove \(p,q\) sono due espressioni da determinare, come funzioni dei coefficienti \(a,b\). Sostituendo nell’equazione abbiamo
\[ z^{3}=p+q+ 3\sqrt[3]{pq}z \]Ora scegliamo \(p,q\) in modo che soddisfino il seguente sistema:
\[ \begin{cases} 3 \sqrt[3]{pq}=-a \\ p+ q= -b \end{cases} \]Queste relazioni implicano le seguenti:
\[ \begin{cases} pq =-\dfrac{a^{3}}{27} \\ p+ q= -b \end{cases} \]Questo sistema è equivalente all’equazione quadratica \(z^{2}+bz -\dfrac{a^{3}}{27}\). Le due soluzioni sono le seguenti
\[ p= -\frac{b}{2}+ \sqrt{\frac{b^{2}}{4}+ \frac{a^{3}}{27}} \ , \quad q= -\frac{b}{2}- \sqrt{\frac{b^{2}}{4}+ \frac{a^{3}}{27}} \]Sostituendo queste due soluzioni nella formula \(z = \sqrt[3]{p}+ \sqrt[3]{q}\) avremmo \(9\) valori possibili. Tuttavia, mediante il vincolo \(3 \sqrt[3]{pq}=-a\) otteniamo solo tre valori indipendenti.
Le tre soluzioni dell’equazione di terzo grado sono quindi
In forma estesa otteniamo la formula di Cardano-del Ferro:
\[ \displaystyle z=\sqrt[3]{-\frac{b}{2}+ \sqrt{\frac{b^{2}}{4}+ \frac{a^{3}}{27}}} + \sqrt[3]{-\frac{b}{2}- \sqrt{\frac{b^{2}}{4} + \frac{a^{3}}{27}}} \]Questa formula venne pubblicata da Cardano nella sua opera ‘Ars Magna’, e da lui attribuita a Scipione del Ferro.
Esercizio 4.11
Calcolare le soluzioni dell’equazione \(z^{3}=6z+6\).
4.5) Equazioni di terzo grado con coefficienti reali
In genere le tre soluzioni di un’equazione di terzo grado sono dei numeri complessi, non necessariamente distinti. Nel caso in cui i coefficienti sono reali, sappiamo che se \(z=x+iy\) è una soluzione complessa anche il coniugato \(\overline{z}=x-iy\) è una soluzione. La terza soluzione è necessariamente un numero reale.
Consideriamo l’equazione generale di terzo grado
Lo studio degli zeri può essere effettuato ricorrendo agli strumenti dell’analisi matematica. Per valori reali di \(z\), cioè con \(z=x\), il polinomio \(P(x)\) è una funzione reale di variabile reale continua, definita su tutto l’intervallo \((-\infty,+\infty)\), che assume valori negativi e positivi. Per il teorema del valore intermedio esiste almeno un punto reale \(x_{1}\) tale che \(P(x_{1})=0\). Ci sono due possibilità: tre radici reali, oppure una radice reale e due complesse coniugate. Il diagramma seguente illustra i due casi:
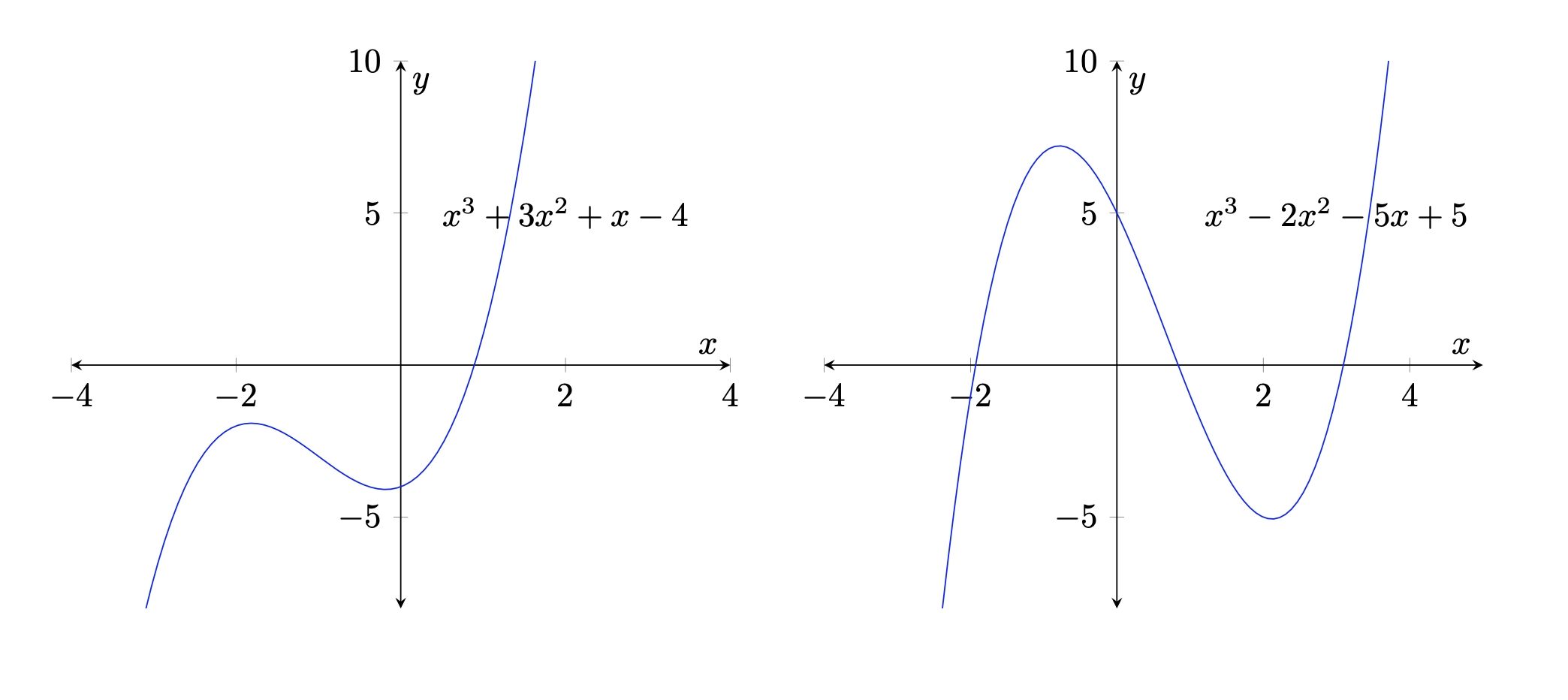
Esercizio 4.12
Dimostrare le seguenti formule
Le tre radici reali possono essere coincidenti, oppure una radice singola e due reali coincidenti.
Le proprietà delle soluzioni dell’equazione con coefficienti reali dipendono dal discriminante dell’equazione. Siano \(z_{1},z_{2},z_{3}\) le soluzioni dell’equazione ridotta di terzo grado \(z^{3}+az+b=0\). Il discriminante dell’equazione è
Per una interpretazione geometrica del discriminante vedere questo articolo.
Se i coefficienti sono reali abbiamo tre casi distinti:
Esercizio 4.13
Trovare le soluzioni dell’equazione \(z^{3}-3z + \sqrt{2}=0\).
Risposta: \(\left[{\sqrt{2},\dfrac{-1-\sqrt{3}}{\sqrt{2}}, \dfrac{-1+\sqrt{3}}{\sqrt{2}}}\right]\).
Esercizio 4.14
Trovare le soluzioni dell’equazione \(z^{3}-6z -9=0\).
Risposta: \(\left[3,\dfrac{-3+\sqrt{3}i}{2}, \dfrac{-3-\sqrt{3}i}{2}\right]\).
4.6) Le equazioni di quarto grado
Mediante lo stesso procedimento utilizzato per le equazioni di terzo grado, possiamo ridurre l’equazione generale di quarto grado nella seguente forma semplificata, in cui manca in termine di terzo grado:
\[ P(z)=z^{4}+ az^{2}+bz +c=0 \\ \]Cerchiamo di rappresentare il polinomio mediante differenza di due quadrati. È facile verificare la seguente indentità:
\[ P(z)=\left(z^{2}+ \frac{a}{2}+t\right)^{2} – \left(2tz^{2}-bz +\left(t^{2}+at -c + \frac{a^{2}}{2}\right)\right) \]Ora scegliamo il valore del parametro \(t\) in modo che sia nullo il discriminante \(D=b^{2}-8t\left(t^{2}+at -c + \dfrac{a^{2}}{2}\right)\). In questo modo l’ultima espressione nel secondo membro dell’identità è un quadrato perfetto e quindi
\[ P(z)=z^{4}+ az^{2}+bz +c=\left(z^{2}+ \frac{a}{2}+t\right)^{2} -2t\left(z-\frac{b}{4t}\right)^{2} \]Il procedimento per risolvere l’equazione di quarto grado è il seguente. In primo luogo risolviamo l’equazione di terzo grado nella variabile \(t\):
\[ D=b^{2}-8t\left(t^{2}+at -c + \frac{a^{2}}{2}\right)=0 \]Indichiamo con \(t_{1}\) una delle soluzioni. Allora possiamo scrivere
\[ \left(z^{2}+ \frac{a}{2}+t_{1}\right)=\pm \sqrt{2t_{1}}\left(z-\frac{b}{4t_{1}}\right) \]Quindi, risolvendo le due equazioni di secondo grado, otteniamo le \(4\) soluzioni dell’equazione di quarto grado.
Discriminante per l’equazione di quarto grado
Sia data l’equazione ridotta di quarto grado \(P(z)=z^{4}+az^{2}+bz +c =0\) e siano \(z_{1},z_{2},z_{3},z_{4}\) le sue radici. Il discriminante è così definito:
Esercizio 4.15
Dimostrare che il discriminante è
Nel seguente esercizio useremo il metodo di Ferrari.
Esercizio 4.16 – Il problema di Zuanne de Tonini da Coi (1540 ca.)
Dividere il numero \(10\) in tre parti proporzionali \(a,b,c\), tali che il prodotto del primo e del secondo è uguale a \(6\).
Questo problema venne posto da Zuanne de Tonini da Coi a Cardano nel \(1540\). Cardano non riuscì a risolvere il problema. Ci riuscì invece il suo allievo Ferrari.
In base al problema abbiamo \(a+b+c=10\) e \(ab=6\). Inoltre \(\dfrac{a}{b}=\dfrac{b}{c}\).
Indichiamo con \(x\) il termine intermedio \(b\). Con facili calcoli otteniamo la seguente equazione di quarto grado:
Aggiungendo \(6x^{2}\) ad entrambi i membri dell’equazione otteniamo
\[ (x^{2}+6)^{2}= 60x + 6x^{2} \]A questo punto introduciamo una nuova incognita \(y\):
\[ (x^{2}+6+y)^{2}= (2y+6)x^{2} + 60x +(y^{2}+12y) \]Scegliamo la variabile \(y\) in modo che il secondo membro sia un quadrato perfetto. Il discriminante deve quindi essere uguale a zero:
\[ 60^{2}- 4(2y+ 6)(y^{2}+12y)=0 \]Questa è un’equazione di terzo grado che può essere risolta con la formula di Cardano-Tartaglia. Una volta trovata una soluzione, tutte e quattro le soluzioni sono ottenute calcolando le radici quadrate positive e negative di entrambi i membri della nuova equazione di quarto grado.
4.7) Equazioni algebriche di grado maggiore di \(4\)
Abbiamo visto che per le equazioni algebriche di grado minore o uguale a \(4\) le soluzioni possono essere rappresentate mediante delle formule, che contengono i coefficienti dell’equazione combinati con le quattro operazioni e le operazioni di estrazione di radice.
Nel periodo successivo al Rinascimento i matematici cercarono invano di trovare formule simili per equazioni algebriche di grado maggiore di \(4\). Intorno al \(1820\) i matematici Ruffini e Abel dimostrarono che questo problema non ha una soluzione generale.
Il teorema di Abel-Ruffini afferma che, per una equazione di grado maggiore o uguale a \(5\), non esiste una soluzione generale che sia funzione dei suoi coefficienti e contenga solamente un numero finito di operazioni aritmetiche ed estrazioni di radici.
Naturalmente le radici, che esistono per il teorema fondamentale dell’algebra, possono essere calcolate, con il grado di precisione desiderato, con algoritmi numerici come il metodo di Newton-Raphson. Il teorema di Abel-Ruffini riguarda solo la forma che l’espressione delle soluzione può avere. Il teorema afferma che non esiste una soluzione generale in termini di radicali.
Il teorema di Abel-Ruffini tuttavia non esclude che in casi particolari si possa trovare una formula risolutiva, in termini di radicali. Ad esempio, l’equazione \(z^{n}-1=0\) può essere risolta per radicali per ogni intero positivo \(n\).
Esercizio 4.17
Dimostrare che la seguente equazione
è risolubile per radicali.
Il teorema di Abel-Ruffini non fornisce informazioni su quali polinomi possono essere risolti mediante radicali. La soluzione di questo problema è stata in seguito fornita dal matematico francese Galois (1811-1832), mediante la sua brillante teoria dei gruppi di Galois. Per approfondire vedere l’ottimo libro di Hernstein[5].
5) Le funzioni di variabile complessa
Introduciamo ora alcuni concetti elementari relativi alle funzioni di variabile complessa.
Definizione 5.1
Sia \(A\) un insieme di numeri complessi. Una funzione di variabile complessa
è una regola che ad ogni \(z \in A\) associa un unico numero complesso
\[ w=f(z)=u+iv \]Il numero \(w\) viene chiamato valore della funzione in \(z\). L’insieme \(A\) è il dominio della funzione e l’insieme \(W=\{f(z): z \in A\}\) viene chiamato il codominio o immagine della funzione.
Possiamo immaginare una funzione come una trasformazione di un insieme del piano complesso in un altro insieme del piano complesso.
Una funzione di variabile complessa è equivalente ad una coppia di funzioni di due variabili reali, che ad ogni punto \((x,y)\) del dominio di definizione assegna un punto di coordinate \((u(x,y),v(x,y))\) del piano \(\mathbb{R}^{2}\):
In generale con il termine funzione si intende funzione ad un solo valore, in quanto ad ogni valore di \(z\) corrispondente un unico valore di \(w\).
Se ad un valore di \(z\) corrispondono più valori di \(v\) allora parliamo di funzioni a più valori. In questo caso abbiamo una collezione di funzioni, ognuna delle quali viene chiamata determinazione della funzione a più valori. Per avere una funzione ad un solo valore in genere si sceglie una delle determinazioni, chiamata determinazione principale.
Esempio 5.1
Consideriamo la funzione \(f(z)=z^{2}\). In questo caso abbiamo
Quindi \(u(x,y)=x^{2}-y^{2}\) e \(v(x,y)=2xy\).
Se utilizziamo le coordinate polari abbiamo \(z=re^{i\theta}\) e
Quindi \(u(r,\theta)=r^{2}\cos 2\theta\) e \(v(r,\theta)=r^{2}\sin 2\theta\).
Esempio 5.2
Per la funzione \(w =f(z)= \dfrac{z}{|z|}\)abbiamo:
Il dominio è tutto il piano complesso, esclusa l’origine \((0,0)\), mentre il codominio è la circonferenza unitaria, cioè l’insieme di equazione \(|w|=1\).
5.1) Esempi di funzioni ad un solo valore
Polinomi
Le funzioni a valori complessi più semplici sono i polinomi:
Si tratta di funzioni definite su tutto il piano complesso.
Funzione esponenziale complessa
La funzione esponenziale è definita dalla formula di Eulero:
Quindi \(u(x,y)=e^{x}\cos y\) e \(v(x,y)=e^{x}\sin y\). La funzione è definita su tutti i punti del piano complesso. Il codominio è \(\mathbb{C}\setminus \{0\}\).
Esercizio 5.1
Dimostrare le seguenti proprietà della funzione \(f(z)=e^{z}\):
Funzioni trigonometriche complesse
Mediante la funzione esponenziale di Eulero è possibile definire le funzioni trigonometriche anche nel campo complesso. Ad esempio:
Chiaramente si ha \(\sin (-z) = -\sin z\) e \(\cos(-z)=\cos z\).
Esercizio 5.2
Dimostrare le seguenti formule trigonometriche di addizione
Esercizio 5.3
Dimostrare la classica formula
Esercizio 5.4
Dimostrare le seguenti formule di prostaferesi:
5.2) Esempi di funzioni a più valori
L’argomento di un numero complesso
Abbiamo visto in precedenza che l’argomento di un numero complesso è una funzione a più valori. Per avere una funzione ad un solo valore si deve scegliere un insieme di valori compreso in un intervallo di \(360\) gradi. Ad esempio, se scegliamo \(0 \le \text{arg }(z) \lt 2\pi\) abbiamo i seguenti valori:
Il valore dell’argomento aumenta mentre ci muoviamo in senso antiorario intorno all’origine. L’argomento è una funzione continua fino a quando ritorniamo sul semiasse reale positivo delle ascisse, dove si ha una discontinuità. Per evitare la discontinuità si introduce un taglio (branch cut) sul semiasse positivo delle ascisse. In questo modo il dominio della funzione è l’intero piano complesso escluso il taglio.
Se invece scegliamo \(-\pi \lt \text{arg}(z) \le \pi\) abbiamo i seguenti valori:
Anche in questo caso il valore dell’argomento aumenta mentre ci muoviamo in senso antiorario intorno all’origine, assumendo prima valori negativi e poi positivi. L’argomento è una funzione continua fino a quando ritorniamo sul semiasse negativo reale delle ascisse, dove abbiamo una discontinuità. Per evitare la discontinuità introduciamo un taglio sul semiasse negativo delle ascisse.
Come abbiamo visto nei paragrafi precedenti, l’intervallo \(-\pi \lt arg(z) \le \pi\) viene chiamato determinazione principale dell’argomento e indicato con \(Arg(z)\).
La radice di un numero complesso
La radice di un numero complesso è una funzione a più valori. Come abbiamo, visto per ogni numero complesso \(z=re^{i\theta}\) abbiamo \(n\) radici \(n\)-esime:
Esercizio 5.5
Calcolare le radici cubiche di \(z=i\) e il valore principale.
Risposta: \([\exp\left(i\frac{\pi}{6}\right), \exp\left(i\frac{5\pi}{6}\right), \exp\left(i\frac{9\pi}{6}\right);\text{valore principale: }\exp\left(i\frac{\pi}{6}\right)]\)
Il logaritmo di un numero complesso
Come nel caso reale, la funzione logaritmo è definita come l’inversa della funzione esponenziale. Se \( z=e^{w}\), poniamo \(w = \ln z\). Se \(z=re^{(\theta + 2k\pi) i}\), allora
Come si vede il logaritmo è una funzione a più valori, in questo caso a infiniti valori. Per avere una funzione ad un solo valore possiamo scegliere la determinazione principale del logaritmo, corrispondente alla determinazione principale dell’argomento \(-\pi \lt \text{arg}(z) \le \pi\). In altri termini, effettuiamo un taglio sul semiasse negativo dell’asse delle ascisse.
Esercizio 5.6
Calcolare tutti i valori di \(\ln (-1-\sqrt{3}i)\) e determinare il valore della determinazione principale.
Risposta: \([ \ln 2 – \frac{2\pi}{3}i ]\)
Potenze complesse
La funzione radice \(w=\sqrt[n]{z}\), con \(n\) intero positivo, può essere scritta come potenza con esponente razionale, \(w=z^{\frac{1}{n}}\). Per estendere la definizione di potenza al caso generale di esponenti complessi \(w=z^{\alpha}\), possiamo utilizzare la funzione esponenziale:
Poiché il logaritmo è una funzione a più valori anche la potenza è a più valori. Quindi per avere una funzione ad un solo valore dobbiamo prendere una determinazione singola del logaritmo, in genere la determinazione principale descritta in precedenza.
Esercizio 5.7
Calcolare gli infinti valori di \(w=1^{i}\) e il valore della determinazione principale.
Risposta: \( [e^{-2k\pi},k=0,\pm \,\cdots; \text{valore principlale}=1]\)
5.3) Osservazioni sulle funzioni a più valori
Le funzioni radice, potenza e logaritmo definite nel campo complesso sono funzioni a più valori, quindi non mantengono tutte le proprietà valide nel caso reale. Ad esempio la proprietà
\[ \sqrt{ab}= \sqrt{a}\sqrt{b} \]è valida nel caso di \(a,b\) numeri reali positivi. Tuttavia non è più valida in generale nel caso di numeri reali negativi o di numeri complessi.
Esercizio 5.8
Spiegare l’errore nei seguenti passaggi:
Esercizio 5.9
Spiegare l’errore nei seguenti passaggi:
Esercizio 5.10
Sia \(k\) un intero non nullo. Spiegare l’errore nei seguenti passaggi:
Essendo \( e^{1+4k\pi i}=e\), ne deduciamo che deve essere
\[ \begin{array}{l} e^{-4k^{2}\pi^{2}}= 1 \end{array} \]chiaramente una contraddizione.
6) Numeri complessi e geometria
Ad ogni numero complesso \(z=x+iy\) possiamo associare il vettore \(\vec{OP}\) che parte dall’origine \(O\) delle coordinate e termina nel punto \(P=(x,y)\). Il numero complesso \(z\) è quindi rappresentato dal vettore \(\vec{OP}\), oppure semplicemente dal punto \(P\). Possiamo quindi parlare indifferentemente di argomento del numero complesso o di angolo del vettore corrispondente.
Le operazioni effettuate sui numeri complessi possono essere visualizzate come operazioni sui vettori corrispondenti. Ad esempio la moltiplicazione di due numeri complessi \(z_{1},z_{2}\), rappresentati dai vettori \(\vec{OP_{1}},\vec{OP_{2}}\), equivale ad eseguire le seguenti due operazioni:
- ruotare il vettore \(\vec{OP_{1}}\) di un angolo uguale all’argomento di \(z_{2}\), cioè all’angolo del vettore \(\vec{OP_{2}}\);
- moltiplicare il modulo del vettore ottenuto per il modulo del vettore \(\vec{OP_{2}}\).
Nel caso \(z_{2}=\pm i\), la moltiplicazione \(z_{1}z_{2}\) equivale a ruotare il vettore corrispondente a \(z_{1}\) di un angolo uguale a \(\pm \dfrac{\pi}{2}\).
Per effettuare la divisione \(\dfrac{z_{1}}{z_{2}}\) si effettuano le seguenti operazioni:
- ruotare il vettore \(\vec{OP_{1}}\) di un angolo uguale all’opposto dell’argomento di \(z_{2}\);
- dividere il modulo del vettore ottenuto per il modulo del vettore \(\vec{OP_{2}}\).
6.1) Coordinate complesse coniugate
Un punto del piano complesso può essere individuato mediante diversi sistemi di coordinate, ad esempio le coordinate cartesiani ortogonali \((x,y)\) o le coordinate polari \((r,\theta)\).
Un altro sistema di coordinate che è utile per lavorare con i numeri complessi è il sistema delle coordinate complesse coniugate. Dato un punto di coordinate cartesiane \(P=(x,y)\), nelle nuove coordinate il punto viene rappresentato da \(P=(z,\overline{z})\); sono definite dalla seguente trasformazione:
La trasformazione inversa è la seguente:
\[ \begin{array}{l} x= \dfrac{z + \overline{z}}{2} \\ y= \dfrac{z – \overline{z}}{2i} \\\end{array} \]6.2) Prodotto scalare e vettoriale
Come abbiamo visto i numeri complessi possono essere interpretati anche come vettori nel piano. Possiamo quindi definire le operazioni di prodotto scalare e prodotto vettoriale. Siano \(z_{1}=x_{1}+ y_{1}\) e \(z_{2}=x_{2}+ y_{2}\) due numeri complessi. Definiamo il prodotto scalare \(z_{1}\bullet z_{2}\) e il prodotto vettoriale \(z_{1} \times z_{2}\) nel seguente modo:
\[ \begin{array}{l}z_{1} \bullet z_{2}=|z_{1}||z_{2}|\cos \theta = x_{1}x_{2}+ y_{1}y_{2}=\frac{1}{2}(\overline{z_{1}}z_{2}+z_{1}\overline{z_{2}})\\ z_{1} \times z_{2}=|z_{1}||z_{2}|\sin \theta = x_{1}y_{2}-y_{1}x_{2}=\dfrac{i}{2}(z_{1}\overline{z_{2}}-\overline{z_{1}}z_{2})\\
\end{array} \]
6.3) Insiemi di punti del piano
Mediante i numeri complessi possiamo rappresentare in forma compatta i vari oggetti della geometria piana.
Esempio 6.1
Siano dati due punti \(z_{1},z_{2}\) del piano complesso. Il segmento che congiunge i due punti ha equazione
Esempio 6.2
Siano dati due punti \(z_{1},z_{2}\) del piano complesso. Il punto medio \(M\) del segmento che congiunge i due punti è
In termini di coordinate cartesiane:
\[ M = \left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right) \]Esercizio 6.1
Sia dato un triangolo di vertici \(z_{1},z_{2},z_{3}\). Determinare il baricentro del triangolo, cioè il punto di incontro delle \(3\) mediane.
Risposta: [\(\frac{z_{1}+z_{2}+z_{3}}{3}\)]
Naturalmente per formare un triangolo i tre punti non devono essere allineati.
6.4) Parallelismo e perpendicolarità
Esercizio 6.2
Siano dati due triangoli di vertici \(z_{1},z_{2},z_{3}\) e \(w_{1},w_{2},w_{3}\). Dimostrare che i due triangoli sono simili se e solo se
Dimostrazione
Due triangoli sono simili se i lati corrispondenti sono in proporzione e gli angoli corrispondenti sono uguali. Esistono tre criteri di similitudine. Possiamo applicare il secondo, il quale afferma che due triangoli sono simili se hanno due lati proporzionali e gli angoli fra essi compresi uguali. Quindi deve essere
Da queste relazioni deriva la conclusione del teorema.
Siano \(z_{1},z_{2},z_{3}\) le coordinate di tre punti distinti \(A,B,C\) del piano, dove \(z_{k}=x_{k}+ i y_{k}, \ k=1,2,3\). La condizione per l’allineamento dei tre punti \(A,B,C\) è
\[ \frac{z_{2}-z_{1}}{z_{3}-z_{1}} = \text{numero reale} \]La condizione perché i segmenti \(AB, AC\) siano perpendicolari è
\[ \frac{z_{2}-z_{1}}{z_{3}-z_{1}} = \text{numero immaginario puro} \]Esercizio 6.3
Dimostrare che tre punti \(z_{1},z_{2},z_{3}\) sono allineati se e solo se
6.5) Equazione della retta nel piano
Dati due punti del piano \(z_{1},z_{2}\), l’equazione parametrica della retta è
\[ z = z_{1}+ t (z_{2}-z_{1}) \ , \quad t \in \mathbb{R} \]Esercizio 6.4
Dimostrare che l’equazione generale della retta con le coordinate complesse coniugate è la seguente:
dove \(b\) è un numero reale.
6.6) Area del parallelogramma e del triangolo
Esercizio 6.5
Dato un parallelogramma di lati \(z_{1},z_{2}\), dimostrare che l’area è
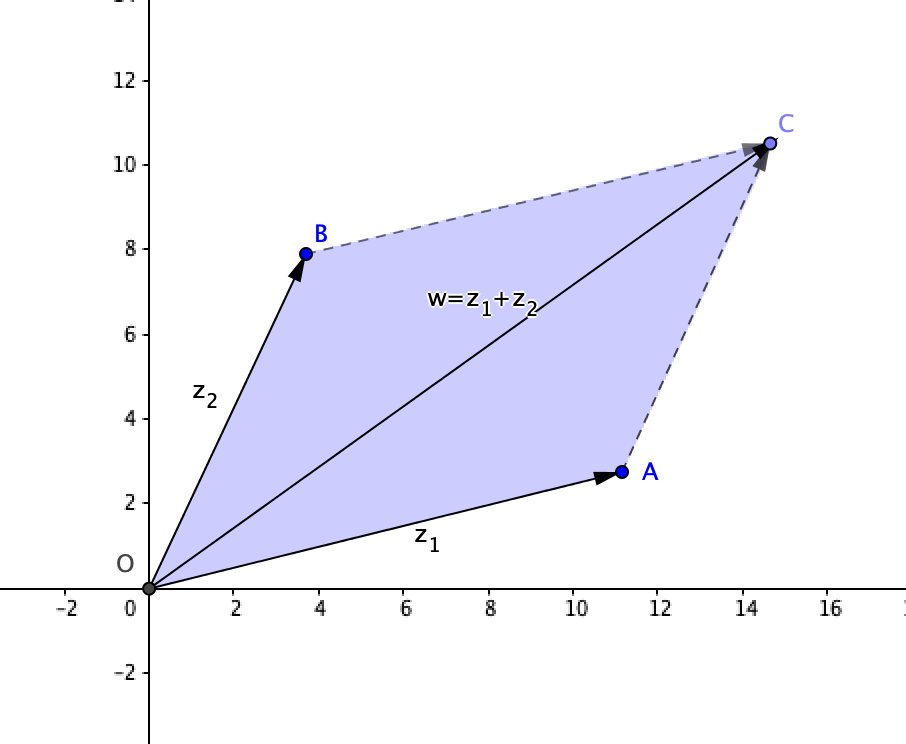
Dato un triangolo di vertici \(z_{1},z_{2},z_{3}\) dove \(z_{k}=x_{k}+ i y_{k}, \ k=1,2,3\), l’area è \(\frac{1}{2}|z_{1}\times z_{2}|\), in quanto è la metà dell’area del parallelogramma corrispondente.
Esercizio 6.6
Dimostrare che l’area del triangolo può essere espressa mediante il seguente determinante:
6.7) Cerchio
Il cerchio di centro l’origine \(O=(0,0)\) e raggio \(R\) ha equazione \(|z|=R\). In generale, il cerchio con centro nel punto \(P_{0}=z_{0}=x_{0}+ iy_{0}\) e raggio \(R\) ha equazione \(|z- z_{0}|=R\). Espandendo in coordinate cartesiane, l’equazione classica del cerchio è
\[ x^{2}+ y^{2} + 2Ax + 2By + C=0 \]dove \(A,B,C\) sono coefficienti reali. Le coordinate del centro sono \((-A,-B)\); il quadrato del raggio è \(A^{2}+B^{2}-C\).
Esercizio 6.7
Dimostrare che, in coordinate complesse coniugate, l’equazione del cerchio è la seguente:
Esercizio 6.8
Determinare le relazioni fra i coefficienti reali \(A,B,C\) e i coefficienti \(a,b,c\).
7) Il teorema di Napoleone
Per dimostrare il teorema di Napoleone utilizziamo il seguente risultato:
Teorema 7.1
Siano \(z_{1},z_{2},z_{3}\) le coordinate dei \(3\) vertici \(A,B,C\) di un triangolo equilatero, orientato positivamente. Allora valgono le seguenti relazioni:
Dimostrazione
Poiché il triangolo è orientato positivamente, il vertice \(C\) è ottenuto da \(B\) mediante una rotazione di un angolo di \(\dfrac{\pi}{3}\) intorno al vertice \(A\). Quindi
Per la seconda identità basta sostituire i valori del seno e coseno ed effettuare i calcoli.
Teorema 7.2 – Teorema di Napoleone
Siano \(z_{1},z_{2},z_{3}\) le coordinate dei \(3\) vertici \(A,B,C\) di un triangolo arbitrario del piano. Su ognuno dei tre lati costruiamo un triangolo equilatero esterno. Allora i tre baricentri dei tre triangoli equilateri formano un altro triangolo equilatero.
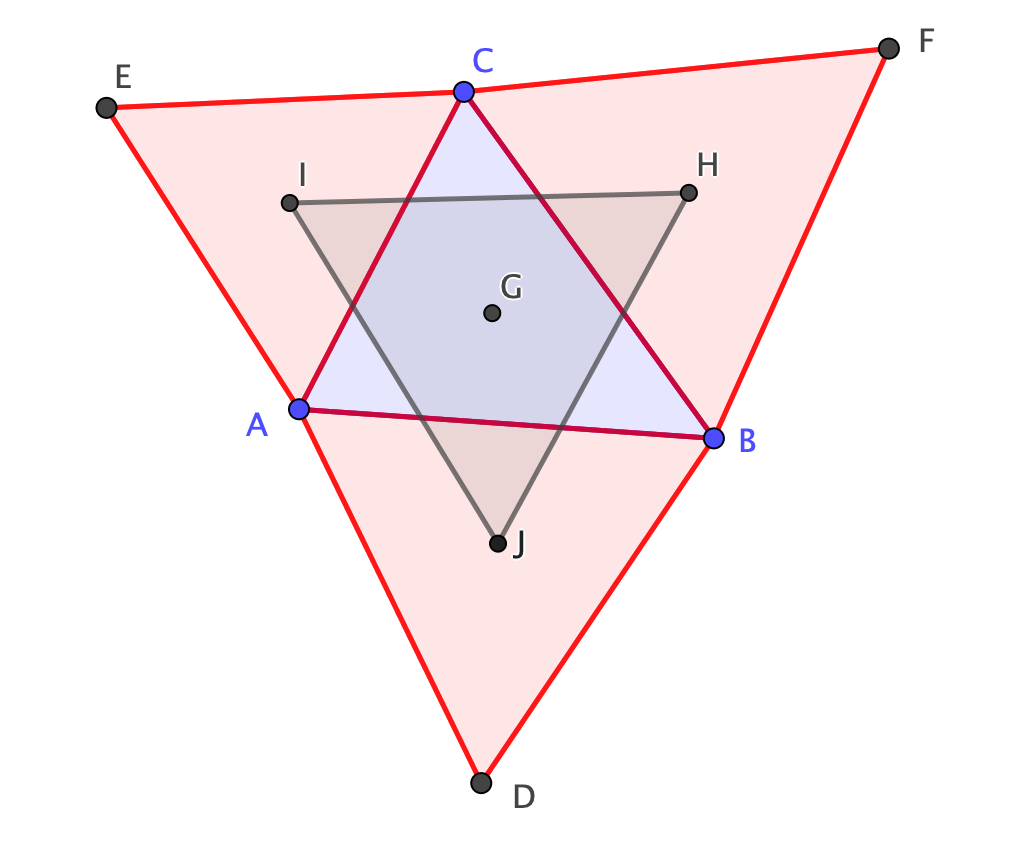
Dimostrazione
Indichiamo con \(\zeta_{1},\zeta_{2},\zeta_{3}\) le coordinate dei tre baricentri, cioè i vertici del triangolo \(\bigtriangleup JHI\), e con \(w_{1},w_{2},w_{3}\) i vertici \(D,F,E\). Per dimostrare che il triangolo \(\bigtriangleup JHI\) è equilatero, basta dimostrare che
Per questo basta applicare il teorema precedente ai tre triangoli equilateri esterni e svolgere i calcoli.
Questo teorema viene attribuito a Napoleone Bonaparte, anche se probabilmente il teorema era già stato dimostrato da altri. Comunque Napoleone aveva un profondo interesse per la matematica e conosceva alcuni dei più important matematici dell’epoca, come Laplace, Lagrange e Legendre.
8) La sfera di Riemann
Consideriamo la seguente proiezione dei punti di una sfera di raggio \(R=1\) e centro nell’origine \((0,0,0)\) sul piano complesso.
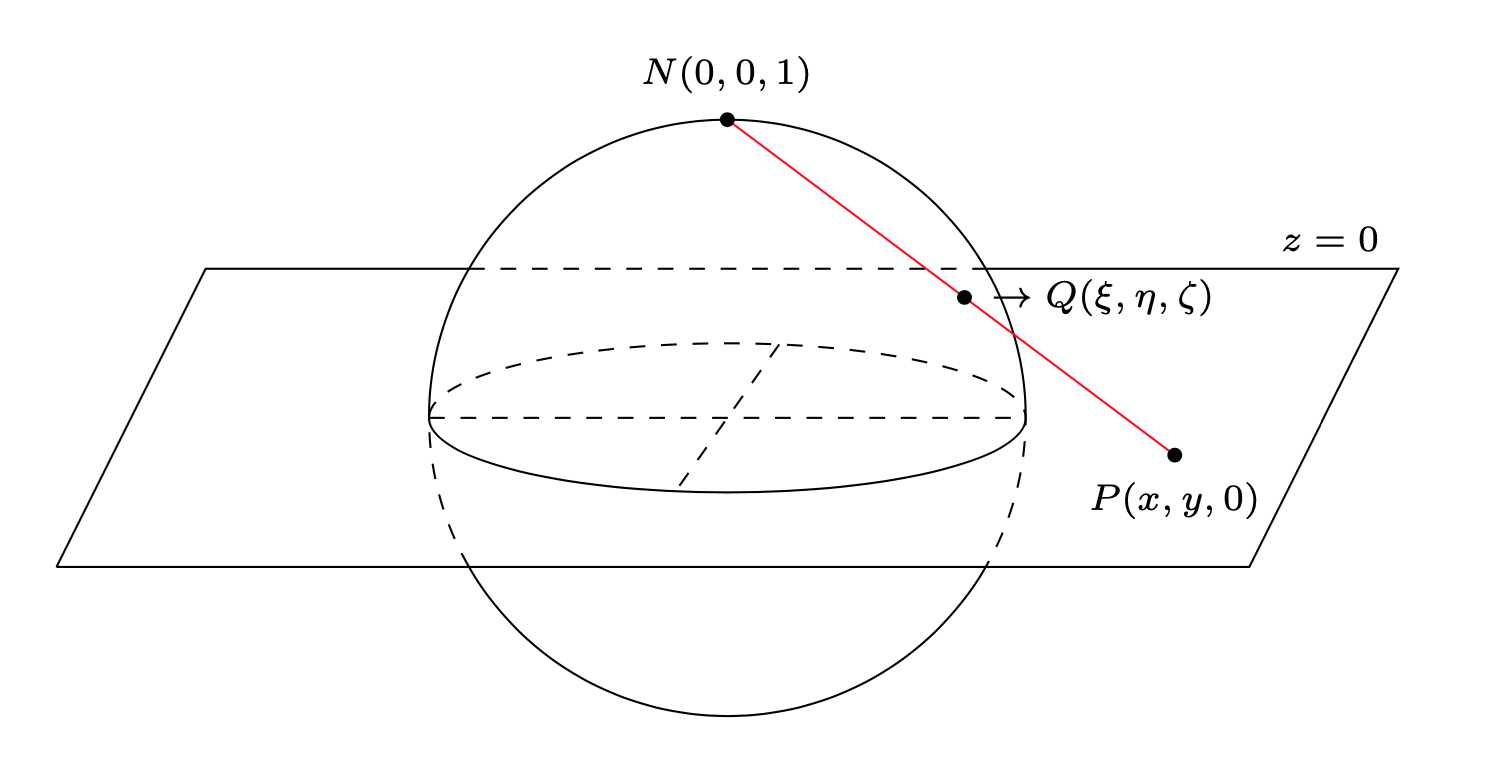
Come si vede, ad ogni punto della sfera corrisponde un unico punto del piano complesso, ad eccezione del polo nord \(N(0,0,1)\). Viceversa, ad ogni punto del piano corrisponde un unico punto sulla sfera.
La sfera si chiama sfera di Riemann e la corrispondenza fra i punti della sfera e i punti del piano complesso si chiama proiezione stereografica.
È utile aggiungere al piano complesso \(\mathbb{C}\) un punto all’infinito, indicato con il simbolo \(\infty\). Il nuovo piano si chiama piano complesso esteso \(\mathbb{C}\cup \infty\).
La proiezione stereografica sulla sfera di Riemann stabilisce quindi una corrispondenza biunivoca fra i punti della sfera e i punti del piano complesso esteso. Il punto all’infinito \(\infty\) è l’immagine del polo nord della sfera \(N(0,0,1)\).
Esercizio 8.1
Dimostrare che le formule per il passaggio dalle coordinate del punto \(z=(x,y)\) del piano complesso esteso alle coordinate tridimensionali del punto \(Q=(\xi, \eta, \zeta)\) sulla sfera sono le seguenti:
Esercizio 8.2
Dimostrare che le formule per il passaggio dalle coordinate tridimensionali del punto \(Q=(\xi, \eta, \zeta)\) della sfera alle coordinate del punto \(z=(x,y)\) del piano complesso esteso sono le seguenti:
Esercizio 8.3
Siano \(z_{1},z_{2}\) due punti finiti del piano complesso esteso. Dimostrare che la distanza euclidea fra le loro immagini sulla sfera di Riemann è
La distanza \(d(z_{1},z_{2})\) si chiama distanza cordale (o distanza sferica) fra i due punti. Dimostrare inoltre che nel caso \(z_{2}=\infty\) si ha
\[ d(z,\infty) = \frac{2}{\sqrt{1+|z_{1}|^{2}}} \]Suggerimento
Ricordare che per un punto \(Q(x,y,z)\) sulla sfera unitaria si ha \(x^{2}+y^{2}+z^{2}=1\).
9) Alcuni esercizi sui numeri complessi
Concludiamo l’articolo con alcuni esercizi che possono essere utili per coloro che vogliono approfondire la loro conoscenza dei numeri complessi.
Esercizio 9.1
Spiegare l’errore dei seguenti passaggi:
Esercizio 9.2
Determinare, con considerazioni geometriche e senza effettuare calcoli, l’angolo \(\theta\), nell’intervallo \(-\pi \lt \theta \le \pi\), tale che \(|e^{i\theta }-1|=2\).
Risposta: \([\theta = \pi]\)
Esercizio 9.3
Come è noto, l’ellisse è il luogo dei punti del piano la cui distanza da due punti fissi, detti fuochi, è costante. La distanza tra i due punti fissi è uguale alla lunghezza dell’asse maggiore dell’ellisse. L’equazione che definisce l’ellisse è la seguente:
dove \(z_{1},z_{2}\) sono i fuochi e \(k\) è una costante positiva reale, che corrisponde alla lunghezza dell’asse maggiore..
Ad esempio, consideriamo l’ellisse con centro nell’origine, con asse maggiore uguale a \(10\) e fuochi nei punti \(F_{1}(-2,0),F_{2}(2,0)\). L’equazione in forma complessa del luogo di punti è
Dimostrare che l’equazione standard, in coordinate cartesiane ortogonali, dell’ellisse precedente è
\[ \frac{x^{2}}{25}+ \frac{y^{2}}{21}=1 \]Esercizio 9.4
Siano \(z_{1},z_{2},z_{3}\) le coordinate dei \(3\) vertici \(A,B,C\) di un triangolo. Allora il triangolo è equilatero se e solo se vale la seguente relazione:
Esercizio 9.5
Dimostrare che due rette \(a_{1}z+ \overline{a_{1}}\overline{z}+ b_{1}=0\) e \(a_{2}z+ \overline{a_{2}}\overline{z}+ b_{2}=0\) sono perpendicolari se e solo se
Esercizio 9.6
Dimostrare la relazione
Suggerimento
Utilizzare la formula \(|z|^{2}=z \overline{z}\).
Esercizio 9.7 – Identità trigonometrica di Lagrange
Dimostrare che, per tutti gli \(z\) tali che \(\sin \dfrac{z}{2}\neq 0\), vale la formula
Esercizio 9.8
Supponiamo che \(z_{1}+z_{2}+z_{3}=0\) e \(|z_{1}|= |z_{2}|=|z_{3}|=1\). Dimostrare che i tre punti sono i vertici di un triangolo equilatero inscritto nel cerchio unitario.
Esercizio 9.9
Supponiamo che i punti \(z_{1},z_{2},\cdots,z_{n}\) siano tutti da un lato di una retta passante per l’origine. Dimostrare che anche i punti \(\dfrac{1}{z_{1}},\dfrac{1}{z_{2}},\cdots, \dfrac{1}{z_{n}}\) hanno una proprietà analoga.
Esercizio 9.10
Dimostrare le seguenti formule
Suggerimento
Espandere \((\cos x + i \sin x)^{5}\) e utilizzare il teorema di De Moivre.
Esercizio 9.11
\[ \begin{array}{l} \sin\dfrac{\pi}{n}\sin\dfrac{2\pi}{n} \cdots \sin\dfrac{(n-1)\pi}{n}= \dfrac{n}{2^{n-1}} \ , \quad n \ge 2 \\ \sin\dfrac{\pi}{2n}\sin\dfrac{3\pi}{2n} \cdots \sin\dfrac{(2n-1)\pi}{2n}= \dfrac{1}{2^{n-1}} \ , \quad n \ge 2 \\ \end{array} \]Suggerimento
Considerare il polinomio
Quindi utilizzare la somma geometrica \(1+z+ \cdots + z^{n-1}=\dfrac{z^{n}-1}{z-1}\) e separare la parte reale e la parte immaginaria, ponendo \(z=1\).
Esercizio 9.12
\[ \begin{array}{l} \Re(z_{1}z_{2})= \Re(z_{1})\Re(z_{2})- \Im(z_{1})\Im(z_{2}) \\ \Im(z_{1}z_{2})= \Re(z_{1})\Im(z_{2})+ \Im(z_{1})\Re(z_{2}) \end{array} \]Conclusione
In questo articolo abbiamo esaminato alcune delle proprietà dei numeri complessi. A partire dai numeri complessi, nel corso del secolo XIX, è stata sviluppata l’analisi complessa, così come a partire dai numeri reali è stata sviluppato il calcolo differenziale e integrale classico. L’analisi complessa è diventata fondamentale in molti settori della matematica e della fisica matematica, come ad esempio la teoria dei numeri e la fisica quantistica. Gli strumenti forniti dall’analisi complessa permettono di risolvere problemi difficili, ad esempio il calcolo di molti integrali, che altrimenti sarebbe molto laborioso risolvere con gli strumenti dell’analisi reale classica. Possiamo riassumere l’importanza dei numeri complessi con le parole del matematico francese Hadamard:
“Le plus court chemin entre deux vérités dans le domaine réel passe par le domaine complexe”.
Jacques Hadamard (1865-1963)
Nei prossimi articoli studieremo come a partire dai numeri complessi è possibile definire i concetti di limite, derivata e integrale, in modo simile a quanto fatto con il calcolo differenziale e integrale di funzioni definite sui numeri reali.
Bibliografia
[1]Van der Waerden – A History of Algebra: From Al-Khwarizmi to Emmy Noether (Springer)
[2]B. Fine, G. Rosenberger – The Fundamental Theorem of Algebra (Springer)
[3]Paul J. Nahin – Dr. Euler’s Fabulous Formula (Princeton UP)
[4]Hans Schwerdtfeger – Geometry of Complex Numbers (Dover)
[5]I. N. Hernstein – Topics in Algebra (Wiley)


0 commenti