Il metodo di esaustione è un procedimento utilizzato dai matematici greci per calcolare la lunghezza di una curva, l’area di una figura piana o il volume di un oggetto tridimensionale. Ad esempio per una figura piana si utilizza un poligono inscritto nella figura: all’aumentare del numero dei lati del poligono, se la successione è definita correttamente, la differenza fra l’area della figura e l’area del poligono può essere resa piccola a piacere. La stessa tecnica può essere utilizzata per calcolare il volume di oggetti tridimensionali, utilizzando al posto dei poligoni altre figure come prismi, cubi, ecc. Di fatto il metodo di esaustione anticipa il calcolo integrale che verrà sviluppato nel XVII secolo, da Newton, Leibniz e altri matematici.
In questo articolo descriveremo alcune applicazioni del metodo di Eudosso, con le quali Archimede riuscì a calcolare le aree e i volumi di molte figure geometriche. Infine analizzeremo il problema degli infinitesimali e il principio di Cavalieri.
1) L’assioma di Eudosso-Archimede
Il metodo di esaustione ha le sue origini nell’antica Grecia. Il nome è legato a Eudosso di Cnido (408 -355 aC), i cui contributi principali sono la Teoria delle Proporzioni e l’Assioma di Eudosso-Archimede, inclusi nel libro V degli Elementi di Euclide.
Il metodo di esaustione si basa su una proposizione, l’assioma di Eudosso, chiamato anche assioma di Eudosso-Archimede, per essere stato utilizzato da Archimede in particolare nella sua opera “Sulla Sfera e il Cilindro”.
L’assioma di Eudosso ha varie formulazioni equivalenti. La più semplice è la seguente:
“date due grandezze aventi un certo rapporto, è possibile trovare un multiplo dell’una che sia maggiore dell’altra”.
Il principio di Eudosso-Archimede sembra ovvio a prima vista, e corrisponde al senso comune della misura delle grandezze reali. Le strutture algebriche nella quali vale il principio di Eudosso-Archimede si chiamano strutture Archimedee. Tuttavia esistono altre strutture algebriche per le quali il principio non è valido. Tali strutture si chiamano non-Archimedee.
Sulla base dell’assioma di Eudosso-Archimede si può dimostrare un teorema che è lo strumento fondamentale del metodo di esaustione:
Teorema 1.1
Date due grandezze omogenee \(A,B\), con \(A \lt B\), se da \(B\) si toglie almeno la sua metà, poi dalla parte restante si toglie almeno la sua metà, e così via, allora dopo un numero finito di passi si ottiene una parte residua più piccola di \(A\).
Una formulazione equivalente in termini moderni è la seguente: dato un numero reale \(\frac{1}{2} \le x \lt 1\), una grandezza \(B \gt 0\) e un numero reale positivo \(\epsilon \gt 0\) arbitrario, allora esiste un intero positivo \(N\) tale che per \(n \gt N\) si ha
\[ B(1-x)^{n} \lt \epsilon \]o in altri termini
\[ \lim_{n \to \infty}B(1-x)^{n}=0 \]Ricordiamo che Aristotele aveva introdotto la distinzione fra infinito potenziale e infinito attuale. L’infinito potenziale consiste nella possibilità di aggiungere sempre qualcosa a una quantità determinata, senza che ci sia mai un elemento ultimo; ad esempio, considerando un insieme finito di numeri naturali \(\{1,2,\cdots,n\}\), possiamo sempre aggiungere \(+1\) all’ultimo numero, senza arrivare mai alla fine. La procedura si può ripetere quante volte si vuole per trovare numeri sempre più grandi.
L’infinito attuale implica l’esistenza di oggetti di misura infinita o di una realtà assegnata avente infiniti elementi. Aristotele nega la possibilità dell’infinito attuale. Nel capitolo VI della Fisica Aristotele scrive che “è impossibile che un continuo sia composto da indivisibili e ogni continuo è divisibile in parti sempre divisibili”.
Tranne poche eccezioni, i matematici, almeno fino a Cantor (1845-1918), hanno preferito evitare l’infinito attuale e utilizzare soltanto il concetto di infinito potenziale.
Il metodo di esaustione di Eudosso permette di evitare di trattare direttamente con grandezze infinite o infinitesime. Per dimostrare che due grandezze omogenee \(A,B\) sono uguali, è sufficiente verificare che non è possibile che sia \(A \lt B\), oppure \(A \gt B\), e quindi per il principio del terzo escluso deve essere \(A=B\).
Per verificare ad esempio che non può essere \(A \lt B\), il metodo di esaustione procede per assurdo. Dimostra che se questa relazione fosse vera, allora la differenza \(B-A\) dovrebbe essere più piccola di una qualsiasi grandezza fissata a piacere. Idem per la relazione \(A \gt B\). Queste contraddizioni portano a concludere che deve essere \(A=B\).
2) Archimede e il calcolo delle aree e dei volumi
Archimede, nato intorno al \(287\) a.C., è considerato il più grande matematico del mondo antico. Le sue opere matematiche principali sono le seguenti:
- Sulle sfera e il cilindro
- Sulla misura del cerchio
- Sui conoidi e sferoidi
- Sulle spirali
- Quadratura della parabola
- Il metodo
Nelle sue opere Archimede applica il metodo di esaustione ad una grande varietà di problemi geometrici, che oggi vengono affrontati normalmente mediante il calcolo integrale. Nei paragrafi successivi analizzeremo alcuni dei principali risultati ottenuti da Archimede.
3) Il cerchio
Negli ‘Elementi’ di Euclide (Proposizione XII.2) viene dimostrato il teorema:
Teorema 3.1
Le aree di due cerchi stanno fra loro come i quadrati dei loro raggi.
Per una dimostrazione vedere l’articolo su questo sito.
Come è noto il rapporto costante fra l’area del cerchio e il quadrato del raggio è il numero \(\pi \approx 3,14\).
Altrettanto importante è il teorema secondo il quale il rapporto fra la circonferenza e il raggio di un cerchio è uguale a \(2\pi\):
Questa proprietà tuttavia non viene enunciata in modo esplicito negli Elementi di Euclide. Il problema è che al tempo dei Greci, mentre erano abbastanza definiti i concetti di misura di un’area o di un segmento, non era ancora del tutto chiaro come definire la lunghezza di una curva. Le curve erano considerate degli oggetti geometrici di natura essenzialmente diversa dalle rette e dai segmenti. Non sembrava quindi possibile con gli strumenti della geometria euclidea determinare la lunghezza di una curva, e in particolare di una circonferenza. Come vedremo il problema venne risolto da Archimede.
Nel trattato ‘Sulla misura del cerchio’ sono presenti tre proposizioni, relative all’area del cerchio e all’approssimazione del numero \(\pi\).
3.1) Lunghezza della circonferenza
Per l’approssimazione del numero \(\pi\), Archimede dimostra la proposizione seguente:
Proposizione 3 – Archimede
La circonferenza di ogni cerchio è tripla del diametro e lo supera ancor meno di un settimo del diametro, e di più di dieci settantunesimi.
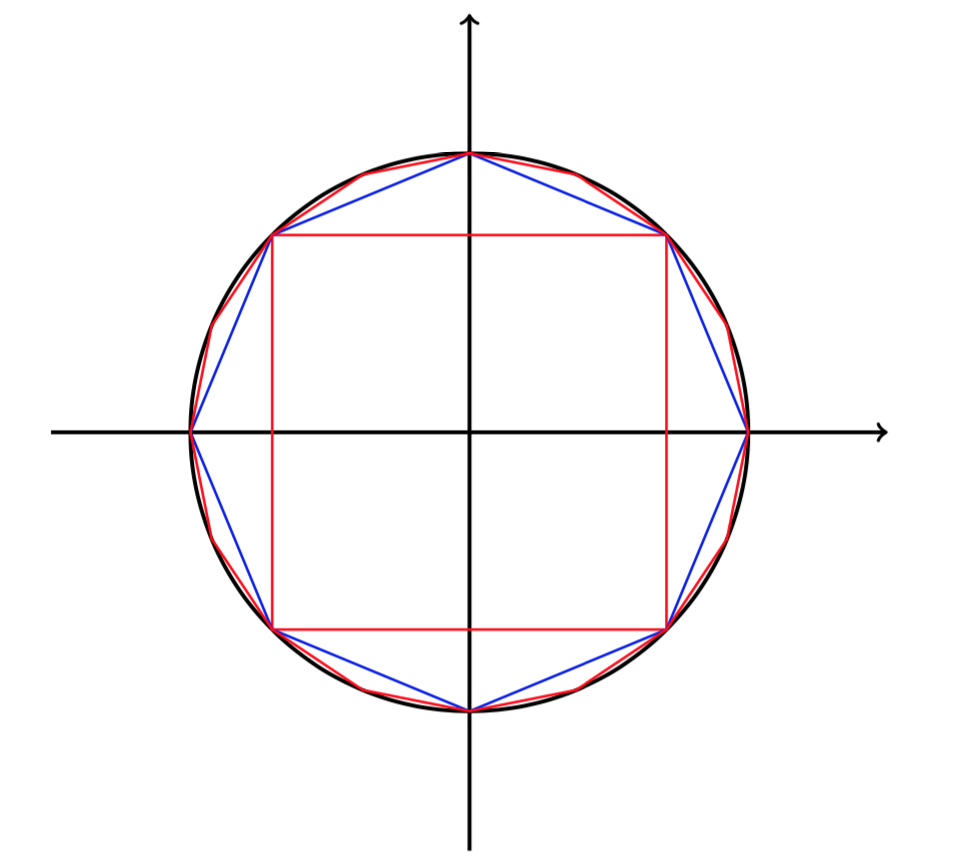
L’idea base di Archimede è che la lunghezza della circonferenza è limitata superiormente dai perimetri dei poligoni regolari circoscritti, e inferiormente dai poligoni regolari inscritti. All’aumentare del numero dei lati la differenza fra la circonferenza e i perimetri può essere resa piccola a piacere. In termini moderni è un passaggio al limite al tendere del numero dei lati all’infinito.
L’approssimazione di Archimede è la seguente:
\[ \frac{223}{71} \lt \frac{C}{2r} \lt \frac{22}{7} \]Per i dettagli dell’algoritmo di Archimede vedere l’articolo pubblicato in questo sito.
3.2) Area del cerchio
Per l’area del cerchio Archimede dimostra la seguente:
Proposizione 1 – Archimede
Ogni cerchio è equivalente ad un triangolo rettangolo che ha l’altezza uguale al raggio e la base uguale alla lunghezza della circonferenza .
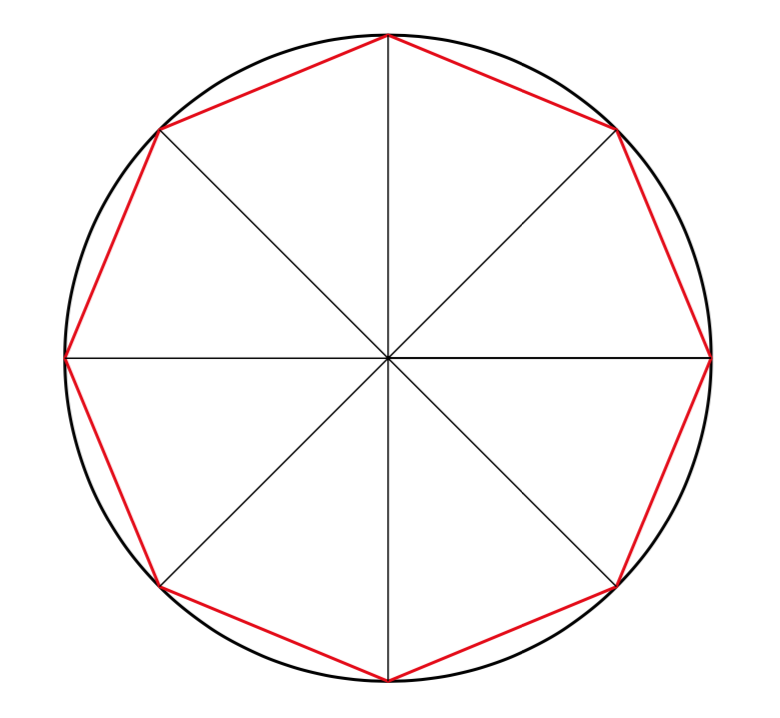
Dimostrazione intuitiva
Nella figura precedente vediamo che all’aumentare del numero dei triangoli le altezze dei triangoli si avvicinano alla lunghezza del raggio. La somma delle basi dei triangoli si avvicina alla lunghezza della circonferenza, che vale \(2 \pi r\). Quindi possiamo approssimare l’area del cerchio \(A\) con il limite della somma delle aree dei triangoli, cioè
\[ A = \frac{2 \pi r \cdot r}{2}= \pi r^{2} \]Dimostrazione con il metodo di esaustione
Indichiamo con \(T\) l’area del triangolo rettangolo che ha l’altezza uguale al raggio e la base uguale alla circonferenza. Supponiamo prima che \(A-T=\epsilon >0\). Nella figura precedente il poligono di \(8\) lati è inscritto nel cerchio e sicuramente la sua area \(P\) è minore di \(T\) (\(P < T\)). Supponiamo ora di raddoppiare i lati del poligono aggiungendo un vertice nel punto centrale di ogni coppia. Denotiamo con \(P^{(1)}\) l’area del nuovo poligono. Si verifica facilmente che
Per il teorema 1.1, proseguendo con questo procedimento possiamo arrivare ad un poligono \(P^{*}\) tale che
\[ A-P^{*} \lt A-T=\epsilon \]e quindi dovrebbe essere \(P^{*} \gt T\). Tuttavia, poiché il poligono di area \(P^{*}\) è inscritto, sicuramente deve essere \(P^{*} < T\). Abbiamo quindi una contraddizione e l’ipotesi di partenza \(A-T >0\) non è vera. In modo simile si dimostra l’impossibilità dell’ipotesi \(A-T < 0\). L’unica possibilità che rimane è quindi \(A=T\).
Una conseguenza immediata dei teoremi di Archimede è il seguente teorema:
Teorema 3.2
Tutti i cerchi sono simili. Cioè il rapporto fra la circonferenza e il raggio è costante:
Si tratta di una proprietà caratteristica della geometria euclidea. Nella geometrie non euclidee, ellittica e iperbolica, in cui non vale il postulato della parallele di Euclide, tale rapporto non è costante.
4) La sfera
I risultati principali relativi alla sfera ottenuti da Archimede sono contenuti nella sua opera ‘Sulla sfera e il cilindro’. Archimede fu il primo a trovare le formule per il calcolo della superficie e del volume della sfera.
4.1) Il principio di Cavalieri
Prima di introdurre i risultati di Archimede, ricordiamo un principio importante, enunciato da Bonaventura Cavalieri (1598-1647). Cavalieri pubblicò la ‘Geometria indivisibilubus continuorum nova quadam ratione promota’ (1635), contenente i principi della teoria degli indivisibili. Il concetto base consiste nella rappresentazione delle grandezze geometriche come costituite da infiniti elementi primitivi. Cavalieri sostiene ad esempio che una figura piana è formata da infinite linee indivisibili, mentre una figura solida è formata da infinite figure piane indivisibili.
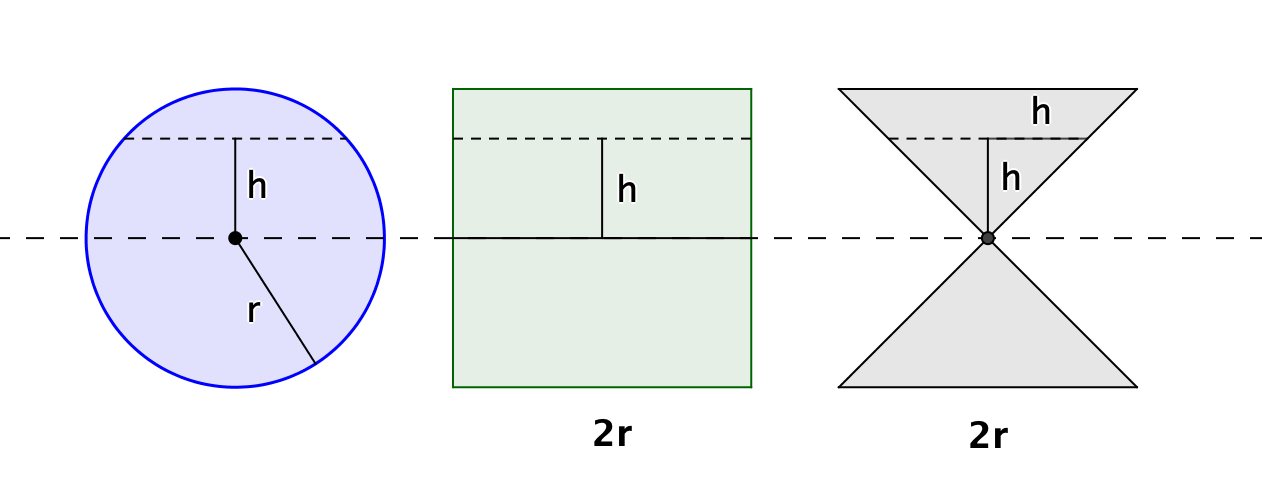
Principio di Cavalieri in due dimensioni
Siano date due regioni del piano comprese fra due rette parallele. Se ogni retta parallela a queste interseca le due regioni in segmenti della stessa lunghezza, allora le due regioni hanno la stessa area.
Principio di Cavalieri in tre dimensioni
Siano date due regioni dello spazio (solidi) comprese fra due piani paralleli. Se ogni piano parallelo a questi interseca le due regioni in sezioni della stessa area, allora le due regioni hanno lo stesso volume.
Il metodo di Cavalieri prevede di suddividere le figure in elementi di misura piccolissima, gli indivisibili, e poi sommare i contributi di ciascuno di essi. Questo metodo venne criticato da diversi matematici, che invece calcolavano i volumi e le aree come facevano Archimede ed Euclide, tramite il metodo per esaustione.
Nonostante non avesse il rigore matematico necessario, il principio degli indivisibili di Cavalieri è considerato l’embrione del calcolo integrale che nel diciassettesimo secolo venne sviluppato ad opera di Torricelli, Barrow, Leibniz e Newton.
4.2) Volume della sfera
Prima di Archimede era nota la seguente proprietà della sfera:
Teorema 4.1
I volumi di due sfere stanno tra loro come i cubi dei rispettivi raggi:
Il volume della sfera viene determinato da Archimede nella proposizione 34 del testo ‘Sulla sfera e il cilindro’.
Proposizione 34 – Archimede
Ogni sfera è quattro volte il cono che ha la base uguale al cerchio massimo della sfera e altezza uguale al raggio della sfera.
In modo equivalente, il volume della sfera è uguale ai \(\dfrac{2}{3}\) del volume del cilindro la cui base è uguale al cerchio massimo della sfera e l’altezza è uguale al diametro.
Dimostrazione
Il teorema si bassa sull’osservazione che il volume del dominio compreso fra il cilindro e la sfera, è uguale al doppio del volume del cono.
Fissata un’altezza \(h\) consideriamo le \(3\) superfici di rotazione:
\[ \begin{array}{l} S_{1}= \pi r^{2} \quad \text{cilindro} \\ S_{2}= \pi (r^{2}-h^{2}) \quad \text{cerchio} \\ S_{3}= \pi h^{2} \quad \text{cono} \\ \end{array} \]È facile verificare che \(S_{2}=S_{1}-S_{3}\).
A questo punto Archimede applica sostanzialmente il principio di Cavalieri. La relazione fra le sezioni \(S_{1},S_{2}, S_{3}\) si estende ai volumi corrispondenti. Quindi abbiamo
Conoscendo le formule del volume del cono e del cilindro, si arriva al volume della sfera:
\[ V(\text{sfera})= 2 \pi r^{3}- 2\frac{1}{3}\pi r^{3}= \frac{4}{3}\pi r^{3} \]4.3) Superficie della sfera
Nel trattato ‘Sulla sfera e il cilindro’ Archimede dimostra il seguente risultato:
Proposizione 33
La superficie della sfera è quattro volte l’area del suo massimo cerchio.
Dimostrazione
Archimede considera una sfera di superficie \(S\) e raggio \(r\), e un cerchio la cui superficie \(T\) è quadrupla di quella del cerchio di raggio massimo, e dimostra che \(S=T\), mediante il classico metodo di esaustione.
Vengono fatte due ipotesi:
a) \(S \gt T\)
b) \(S \lt T\)
Procedendo con il metodo di esaustione, dimostra che nessuna delle due ipotesi può essere vera e quindi deve esser \(S=T\).
Per i dettagli della dimostrazione vedere il testo di Heath [1].
Seconda dimostrazione
Supponiamo la sfera come contenente un certo numero di piramidi, con vertice nel centro della sfera e altezza uguale al raggio. La superficie \(S\) della sfera viene approssimata con la somma delle aree di base delle piramidi. Il volume di ogni piramide con base \(A\) è \(V=\dfrac{1}{3}Ar\). Indichiamo con \(A_{1},\cdots,A_{n}\) le superfici delle basi delle piramidi. Il volume della sfera è quindi approssimativamente
\[ V \approx \frac{1}{3}(A_{1}+ \cdots + A_{n})r \]Al crescere di \(n\) la somma delle aree delle basi delle piramidi tende alla superficie della sfera, e quindi
\[ V = \frac{1}{3}Sr \]Poiché sappiamo che \(V=\dfrac{4}{3}r^{3}\), possiamo calcolare la superficie \(S\):
\[ S = 4 \pi r^{2} \]5) Quadratura parabola
Ricordiamo che una conica è una curva piana ottenuta intersecando un cono circolare retto con un piano. Le coniche sono state oggetto di studio di Apolllonio di Perga (262 a.C – 190 a.C) intorno al \(200\) a.C. Esistono tre tipi fondamentali di coniche:
- ellisse
- iperbole
- parabola
La circonferenza è un caso particolare di ellisse.
Prima di Archimede nessuno era stato in grado di calcolare le aree delle regioni delimitate dalle coniche. Nella sua opera ‘Quadratura della parabola’ Archimede affronta il problema di calcolare l’area di un segmento parabolico, cioè della regione del piano compresa fra un arco di parabola e il segmento che ha gli estremi dell’arco.
Dato un segmento parabolico con base \(AB\), il punto \(O\) del segmento che ha la massima distanza dalla base viene chiamato il vertice del segmento, il segmento perpendicolare da \(O\) al segmento \(AB\) è la sua altezza. Notiamo che in genere il vertice del segmento non coincide con il vertice della parabola, che è il punto intersezione della parabola con il suo asse di simmetria.
Mediante il metodo di esaustione Archimede riesce a dimostrare la seguente:
Proposizione 17
L’area di un segmento di parabola è uguale ai \(\dfrac{4}{3}\) dell’area del triangolo che ha come base il segmento ed uguale altezza.
Nella figura seguente per semplicità abbiamo disegnato un segmento parabolico simmetrico; tuttavia il teorema di Archimede vale anche nel caso di un segmento parabolico obliquo.
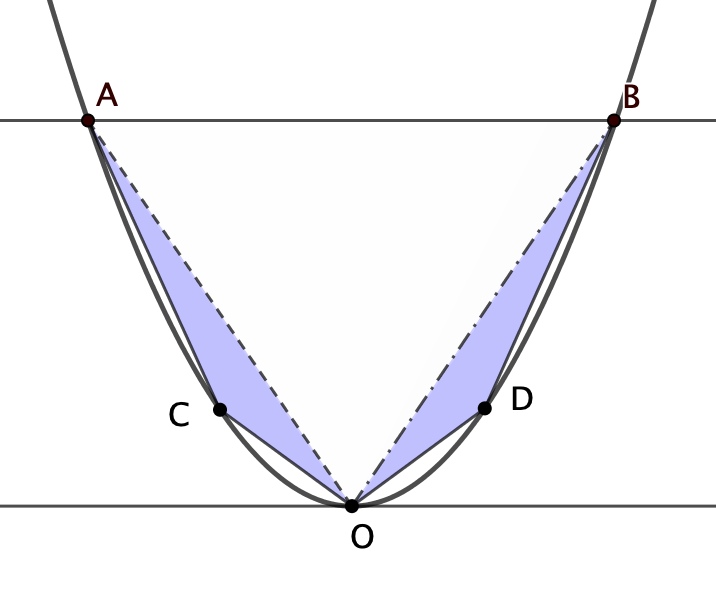
Archimede costruisce una successione di poligoni che gradualmente coprono tutta l’area del segmento di parabola. Il primo poligono è il triangolo \(\triangle{AOB}\). Il successivo è costituito dai due triangoli \(\triangle{ACO}\) e \(\triangle{BDO}\). Continuando il processo otteniamo un insieme di triangoli che ricoprono il segmento parabolico. In termini moderni possiamo affermare che l’area \(A\) del segmento parabolico è
\[ A= \lim_{n \to \infty}A_{n} \]Indicata con \(A_{0}\) l’area del primo triangolo, Archimede dimostra che l’area del secondo poligono (costituito da due triangoli) è \(A_{1}=\dfrac{1}{4}A_{0}\). Proseguendo con la costruzione si trova la formula generale \(A_{n}=\dfrac{1}{4}A_{n-1}\). Quindi l’area del segmento parabolico è data dalla somma della seguente serie:
\[ A= \left(1 + \frac{1}{4}+ \frac{1}{4^{2}}+ \frac{1}{4^{3}}+ \cdots \right)A_{0} = \frac{1}{1- \frac{1}{4}}A_{0}=\frac{4}{3}A_{0} \]dove abbiano applicato il noto risultato relativo alla serie geometrica \(\sum_{n=0}^{\infty}x^{n}=\dfrac{1}{1-x}\) se \(|x| \lt 1\).
Archimede non parla di somma della serie infinita, perché ai suoi tempi i concetti di limite e somma di serie non erano ancora stati definiti. Invece ricorre al metodo della riduzione all’assurdo, dimostrando che l’area del segmento parabolico non può essere né minore né maggiore di \(\dfrac{4}{3}A\). Per la dimostrazione completa di Archimede vedere il testo di Heat.
Esercizio 5.1
Dimostrare la seguente formula della somma geometrica:
utilizzando ripetutamente la seguente relazione:
\[ \frac{1}{4^{k}}+ \frac{1}{3}\frac{1}{4^{k}} =\frac{1}{3}\frac{1}{4^{k-1}} \]Conclusione
Il principio di Eudosso-Archimede e i risultati di Archimede anticipano molte delle idee e metodi del calcolo integrale, che verrà sviluppato da Newton, Leibniz e altri. Uno dei concetti fondamentali dell’analisi matematica è il concetto di limite, la cui definizione rigorosa è stata data da Cauchy (1789-1857). La definizione dei fondamenti dell’analisi matematica ha permesso di chiarire e comprendere i metodi utilizzati da Archimede e verificarne la sostanziale correttezza logica.
Bibliografia
[1]T. Heath – The Works of Archimedes (Dover)
[2]T. Heath – A History of Greek Mathematics (Vol. I,II; Dover)
[3]C. H. Edwards – The Historical Development of the Calculus (Springer)

4 commenti
nicola · 9 Agosto 2022 alle 2:41 PM
quanto è interessante esplorare il mondo ‘geometrico’ dei greci. grazie per questo sunto. Ho dei dubbi sul fatto che Archimede abbia usato il metodo descritto al punto 4.2 poichè, mi sembra, sia un metodo algebrico. Mi piacerebbe un suo commento. Inoltre; per dedurre il volume della sfera bisogna conoscere il volume del cilindro e del cono: come avevano dimostrato il loro valore ?
gameludere · 12 Agosto 2022 alle 2:29 PM
Ciao Nicola, grazie per il commento.
Per calcolare il volume del cilindro si opera come per il volume di un prisma: si calcola l’area di base e si moltiplica per l’altezza. Questo era noto ai Greci. Naturalmente è necessario saper calcolare l’area del cerchio di base. Negli Elementi di Euclide si dimostra che l’area del cerchio è proporzionale al quadrato del raggio. La costante di proporzionalità \(\pi\) è un numero irrazionale, che Archimede riuscì ad approssimare come un valore compreso fra \(\dfrac{22}{7}\) e \(\dfrac{223}{71}\).
I volumi della piramide e del cono sono calcolati negli Elementi di Euclide (libro XII) mediante il metodo di esaustione di Eudosso. Nello stesso libro viene data la dimostrazione della relazione fra il volume del cono e del cilindro, sempre utilizzando il metodo di esaustione di Eudosso.
Per i dettagli è utile studiare direttamente gli Elementi di Euclide. Ad esempio vedi http://www.scienzaatscuola.it/euclide/libro12.html, oppure in lingua inglese http://aleph0.clarku.edu/~djoyce/elements/elements.html.
Per quanto riguarda le notazioni simboliche, ricordiamo che l’algebra simbolica è stata sviluppata nel periodo del Rinascimento. Quindi Euclide, Archimede e gli altri matematici dell’antichità esprimevano i concetti e teoremi matematici mediante parole e diagrammi geometrici.
Enrico · 31 Marzo 2023 alle 6:21 PM
A proposito del teorema 1.1 a me sembra che lim(1-1/x)^n = 0 vale anche per 0 < x < 1/2. Non è quindi inutilmente restrittiva la condizione 1/2<=x<1? Mi sfugge qualcosa?
gameludere · 2 Aprile 2023 alle 3:03 PM
Ciao Enrico! Immagino intendessi scrivere \(x\) invece di \(1/x\) nel tuo commento.
La tua osservazione è corretta, infatti abbiamo \(\lim_{n \to \infty}B(1-x)^{n}=0\) anche per \(0 \lt x \lt 1/2\). Tuttavia il teorema 1.1 non è proprio equivalente al limite indicato. Il teorema 1.1 corrisponde alla proposizione 1 del libro 10 degli Elementi di Euclide. Nella dimostrazione geometrica di Euclide (vedi link) ad ogni passo si suppone di togliere dalla parte rimanente di \(B\) una quantità maggiore od uguale alla metà della parte rimanente (non necessariamente la stessa frazione \(x\) ad ogni passo, purché sia sempre \(x \ge 1/2\)). Questo assicura che dopo un numero finito di passi rimane una grandezza inferiore ad \(A\). Il limite inferiore \(1/2\) è dovuto al fatto che \(\sum_{n=1}^{\infty}2^{-n}=1\). Se ammettiamo valori nell’intervallo \((0 \lt x \lt 1/2)\), con la frazione \(x\) che può variare ad ogni passo, allora il teorema non è più necessariamente vero. Ad esempio se al passo \(n\), con \(n=1,2,\cdots\), prendiamo \(x = 3^{-n}\), allora non è possibile rendere piccola a piacere la parte rimanente della grandezza \(B\).