Nel libro V degli Elementi di Euclide viene illustrata la teoria delle proporzioni, sviluppata da Eudosso di Cnido nella prima metà del secolo IV a.C. La teoria di Eudosso è un esempio del grande livello di astrazione raggiunto dai matematici Greci. Ha permesso di superare la crisi dovuta alla scoperta delle grandezze incommensurabili ed è la base sulla quale verrà costruita la teoria dei numeri reali nel corso del secolo XIX.
In questo articolo descriveremo la teoria delle proporzioni di Eudosso, l’assioma di Archimede e le relazioni con la moderna teoria dei numeri reali.
1) Eudosso e Archimede
Eudosso di Cnido (località dell’odierna Turchia) è un matematico e astronomo greco vissuto intorno al periodo \(408-355\) a.C. circa. Visse al tempo di Platone e frequentò la famosa Accademia, la scuola platonica il cui scopo principale era lo studio della matematica, dell’astronomia e della filosofia. Ha dato importanti contributi in vari settori, tra i quali in particolare:
- la teoria delle proporzioni in geometria.
- il metodo di Eudosso-Archimede che anticipa il calcolo differenziale e integrale di Newton e Leibniz del XVII secolo.
- la creazione di un modello matematico del moto dei corpi celesti. L’universo secondo Eudosso è costituito da un sistema di sfere omocentriche, cioè con un unico centro di rotazione in cui si trova la Terra. La Terra è immobile e al centro dell’universo, circondata da sfere che si muovono con moto circolare uniforme. Le stelle fisse si trovano nella sfera più esterna.
Archimede (287 a.C – 212 a.C) è considerato uno dei più grandi matematici dell’antichità. Ha dato importanti contributi in molti settori della scienza e della tecnologia:
- Geometria e Matematica
- Statica e Dinamica dei corpi rigidi
- Meccanica dei fluidi
- Architettura
- Ottica
Tra i principali risultati di Archimede ricordiamo i seguenti: il postulato di Eudosso-Archimede, il calcolo delle aree e dei volumi, la legge dell’equilibrio dei corpi rigidi, il principio di Archimede sui corpi immersi nell’acqua, ecc.
Per uno studio approfondito delle opere di Eudosso e Archimede, e in generale della matematica greca, vedere [1].
2) La scoperta delle grandezze incommensurabili
La scoperta delle grandezze incommensurabili mise in crisi le fondamenta della Scuola Pitagorica. I Pitagorici concepivano il numero come misura di tutte le cose, la base con cui spiegare la struttura dell’Universo. Per i Pitagorici i numeri erano i numeri interi e questi costituivano il principio di tutta la realtà. Secondo questo punto di vista date due grandezze geometriche è sempre possibile trovare una unità di misura per esprimere entrambe le grandezze come suoi multipli interi. Due grandezze geometriche con questa proprietà vengono chiamate commensurabili. Quindi come logica conseguenza qualunque grandezza nell’universo è commensurabile con tutte le altre.
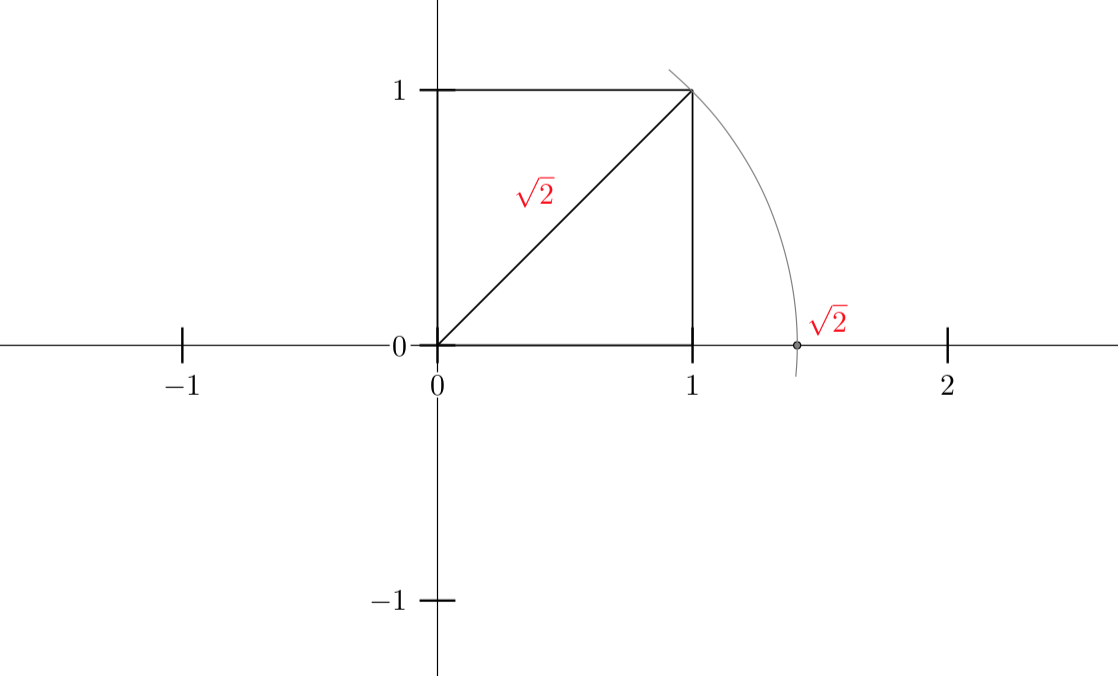
Questa idea fondamentale e brillante venne messa in crisi dal teorema di Pitagora, che era proprio il risultato più importante della Scuola Pitagorica. Ad esempio la diagonale e il lato di un quadrato non sono fra loro commensurabili, come è facile dimostrare:
In termini moderni questo equivale al seguente teorema:
Teorema 2.1
Il numero \(\sqrt{2}\) è irrazionale.
Riportiamo la dimostrazione classica di Euclide. Supponiamo per assurdo che \(\sqrt{2}=\dfrac{a}{b}\) con \(a,b \in\mathbb{Z}\) e \((a,b)=1\). Allora
\[ a^{2}=2b^{2} \]e quindi \(2|a\). Essendo \(a\) un numero pari, possiamo porre \(a=2k\) ottenendo
\[ a^{2}=4k^{2}=2b^{2} \]e quindi
\[ 2k^{2}=b^{2} \]da cui deriva che \(2|b\), contrariamente all’ipotesi che \((a,b)=1\).
Un altro caso di incommensurabilità scoperto dai Greci è il rapporto fra la diagonale e il lato del pentagono regolare. Come è noto tale rapporto viene chiamato numero aureo e vale \(\Phi = \dfrac{1+\sqrt{5}}{2}\).
Questo può essere dimostrato anche per via geometrica. Tracciando le diagonali del pentagono i punti di interazione formano un altro pentagono regolare. Questo processo può essere continuato all’infinito, ottenendo pentagoni sempre più piccoli. Ma questo contraddice contraddice l’ipotesi che il rapporto iniziale della diagonale e del lato possa essere razionale, cioè un rapporto di interi, in quanto la riduzione degli interi si arresta all’unità e non può proseguire all’infinito.
La scoperta delle grandezze incommensurabili pose la necessità di creare una teoria in grado di definire i rapporti fra due grandezze, anche nel caso in cui non è possibile trovare un’unità intera comune. La teoria deve essere in grado di gestire i due casi fondamentali: il rapporto è un numero razionale oppure un numero irrazionale.
La scoperta delle grandezze incommensurabili è la causa principale della prima teoria dei numeri reali, creata da Eudosso e inserita negli Elementi di Euclide. La teoria di Eudosso consiste in due componenti principali:
- la teoria delle proporzioni
- l’assioma di Eudosso-Archimede e il metodo di esaustione
3) La teoria delle proporzioni di Eudosso-Euclide
La forma definitiva della teoria dell proporzioni di Eudosso si trova nel libro V degli Elementi di Euclide. La teoria delle proporzioni di Eudosso si basa su tre concetti base:
- grandezza (magnitudo)
- rapporto (ratio)
- proporzione (proportio)
Grandezza
Questo concetto non viene definito esplicitamente, ma le sue proprietà derivano dalle grandezze geometriche già definite negli Elementi (rette, figure piane, figure solide).
Alcune definizioni di base nel libro V sono le seguenti:
Def.1 – Sottomultiplo
Una grandezza è parte di una grandezza, la minore di quella maggiore quando essa misura la maggiore.
Def.2 – Multiplo
La grandezza maggiore è multipla della minore quando è misurata dalla minore.
Def.4 – Assioma di Eudosso
Si dice che hanno tra loro rapporto quelle grandezze le quali possono, se moltiplicate, superarsi reciprocamente.
Le operazioni di base sulle grandezze geometriche sono le seguenti:
- confronto
- moltiplicazione
- somma
- sottrazione
In termini moderni, nell’insieme delle grandezze geometriche si suppone definita una relazione di ordinamento totale, che possiamo indicare con il simbolo “\(>\)”. Date due grandezze geometriche \(A,B\) abbiamo quindi tre casi:
\[ \begin{array}{l} A \gt B \quad \text{A maggiore di B} \\ B \gt A \quad \text{B maggiore di A} \\ A = B \quad \text{Se le precedenti sono false} \\ \end{array} \]Def.3 – Rapporto
È una certa relazione tra due grandezze allo stesso tipo, in ordine alla loro quantità.
È una definizione generica e non utile dal punto di vista operativo. Il rapporto è limitato a grandezze omogenee e l’unico parametro importante è la quantità.
Nel caso della proporzione viene data una definizione operativa completa:
Def.5 – Proporzione
Si dice che quattro grandezze hanno lo stesso rapporto, la prima alla seconda come la terza alla quarta, quando presi equimultipli della prima e della terza secondo qualsiasi altro numero, e equimultipli della seconda e della quarta secondo qualsiasi altro numero, se il multiplo della prima è maggiore di quello della seconda, anche il multiplo della terza sarà maggiore di quello della quarta; se uguale, uguale; se minore, minore.
Possiamo tradurre la definizione testuale in simboli. Date quattro grandezze \(A,B,C,D\) diciamo che
\[ A:B = C:D \]se per ogni coppia di interi positivi \(n,m\) si ha
\[ \begin{array}{l} mA \gt nB \quad \text{se e solo se} \quad mC \gt nD\\ mA \lt nB \quad \text{se e solo se} \quad mC \lt nD\\ mA = nB \quad \text{se e solo se} \quad mC = nD\\\end{array} \]Def.7 – Rapporto maggiore
Date quattro grandezze e presi equimultipli della prima e della terza e altri equimultipli della seconda e della quarta, se il multiplo della prima è maggiore di quello della seconda, ma il multiplo della terza non è maggiore di quello della quarta, allora diremo che il rapporto della prima alla seconda è maggiore di quello della terza alla quarta.
In termini moderni si ha \( A:B \gt C:D\) se per ogni coppia di interi positivi \(n,m\) risulta
\[ mA \gt nB \quad \text{ma} \quad mC \le nD \]Questa relazione può essere scritta nel seguente modo:
\[ \frac{C}{D} \le \frac{n}{m} \lt \frac{A}{B} \]Sostanzialmente fra i due rapporti è possibile inserire un numero razionale.
Queste definizioni sono molto importante e brillanti. Di fatto la teoria di Eudosso anticipa la teoria dei numeri reali che verrà sviluppata nel corso del secolo XIX da Dedekind e altri matematici.
4) L’assioma di continuità di Eudosso-Archimede
Un’altro importante concetto sviluppato da Eudosso è il cosiddetto postulato di Archimede o assioma di Archimede, che esprime una proprietà fondamentale dell’insieme dei numeri reali. L’assioma è riportato nel libro V, proposizione 4, degli Elementi di Euclide:
“Sono dette avere un rapporto tra loro quelle grandezze che sono capaci, se moltiplicate, di eccedersi tra loro.”
Questo postulato viene anche chiamato assioma di continuità. In termini moderni l’assioma di Eudosso-Archimede può essere espresso in diversi modi equivalenti.
La formulazione più semplice è la seguente:
Assioma di continuità (I)
Sia \(x\) un numero reale. Allora esiste un numero naturale \(n\) tale che:
Una versione equivalente è la seguente:
Assioma di continuità (II)
Dati due numeri reali \(a,b\), con \(a \gt 0\), allora esiste un intero positivo \(n\) tale che
Una versione geometrica è la seguente:
Assioma di continuità (III)
Dati comunque due segmenti di lunghezza rispettivamente \(L_{1},L_{2}\), con \(L_{1} \lt L_{2}\), esiste sempre multiplo intero di \(L_{1} \) che è maggiore di \(L_{2}\).
Un’altra versione interessante, molto utile nelle dimostrazioni, è la seguente:
Assioma di continuità (IV)
Date due grandezze omogenee \(A,B\), con \(A \lt B\), se da \(B\) si toglie almeno la sua metà, poi dalla parte restante si toglie almeno la sua metà, e così via, allora dopo un numero finito di passi si ottiene una parte residua più piccola di \(A\).
Sostanzialmente, l’assioma di Eudosso-Archimede afferma che non possono esistere numeri infinitamente piccoli o numeri infinitamente grandi. L’esempio fondamentale di campo numerico nel quale vale il postulato di Archimede è il campo dei numeri reali \(\mathbb{R}\).
Nonostante il postulato di Archimede possa sembrare ovvio, va ricordato che esistono esempi di campi numerici che non soddisfano il postulato, e vengono chiamati campi non archimedei.
Il metodo di esaustione
L’assioma di Eudosso-Archimede è alla base del metodo di esaustione. Si tratta di una procedura per calcolare lunghezze, aree e volumi. Ad esempio per calcolare l’area di una figura piana si inscrive un poligono all’interno della figura. Quindi si aumenta il numero dei lati in modo che l’area del poligono converga al valore dell’area della figura. In molte situazioni è possibile scegliere i poligoni in modo che la parte di area compresa fra la figura piana e il poligono diventa arbitrariamente piccola, all’aumentare del numero dei lati del poligono.
Il metodo di esaustione essenzialmente anticipa il calcolo integrale moderno, in particolare il calcolo dell’integrale di Riemann come limite delle cosiddette somme di Riemann.
Mediante il metodo di esaustione Archimede è riuscito a calcolare il valore del numero irrazionale \(\pi\), dal quale poi si può calcolare la lunghezza della circonferenza. Per i dettagli sul metodo di Archimede vedere l’articolo in questo sito.
Un esempio di utilizzo dell’assioma di continuità presente negli Elementi di Euclide è la dimostrazione del seguente teorema:
Teorema 4.1
Le aree di due cerchi stanno fra loro come i quadrati dei loro raggi.
Dimostrazione
Siano \(A_{1},A_{2}\) le aree di due cerchi di raggi \(r_{1},r_{2}\). Vogliamo dimostrare che
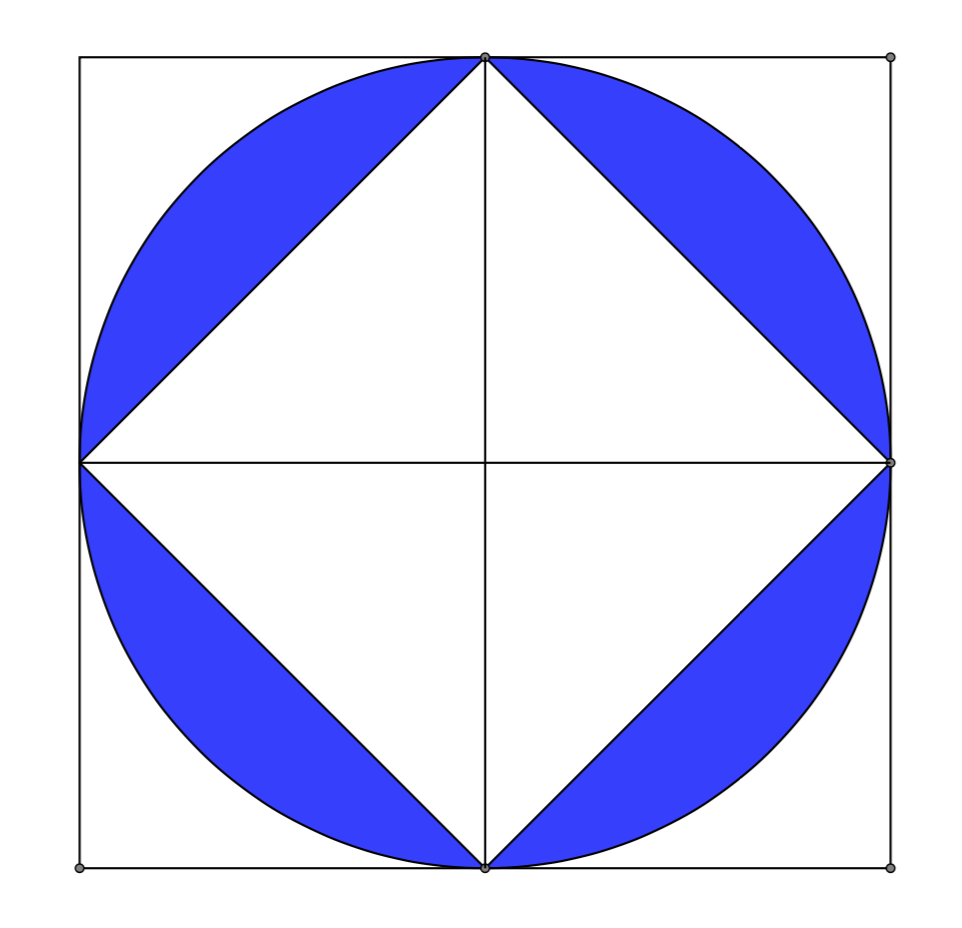
Nella figura sopra il quadrato circoscritto è costituito da \(8\) triangoli rettangoli isosceli uguali, mentre il quadrato inscritto è costituito da \(4\) triangoli rettangoli uguali ai precedenti. L’area in colore è chiaramente minore dell’area del quadrato inscritto. Quindi la differenza fra l’area del cerchio e l’area del quadrato inscritto è minore della metà dell’area del cerchio. Se proseguiamo con poligoni regolari di \(8,16,\cdots\), lati, l’area in colore diventerà sempre più piccola. Possiamo ora applicare l’assioma di continuità. Sia \(\varepsilon\) un numero reale piccolo a piacere e sia \(P_{1}\) l’area del poligono regolare di \(n\) lati. Prendendo \(n\) sufficientemente grande, per l’assioma di continuità avremo
\[ A_{1}-P_{1} \lt \varepsilon \]Supponiamo ora che la proporzione
\[ A_{1}:A_{2}=r_{1}^{2}:r_{2}^{2} \]non sia vera e che l’area \(A_{1}\) sia troppo grande per la proporzione. Allora esisterà una grandezza reale positiva \(\delta\) tale che
\[ (A_{1}- \delta): A_{2}=r_{1}^{2}:r_{2}^{2} \]Tuttavia se prendiamo \(n\) abbastanza grande, tale che \(\varepsilon \le \delta\), avremo
\[ A_{1}- P_{1} \lt \varepsilon \le \delta \]Il poligono regolare con lo stesso numero di lati \(n\) inscritto nel secondo cerchio verifica chiaramente \(P_{2} \lt A_{2}\), quindi mettendo insieme abbiamo
\[ \begin{array}{l} A_{1}-\delta \lt P_{1} \\ A_{2} \gt P_{2} \\ \dfrac{P_{1}}{P_{2}} \gt \dfrac{A_{1}-\delta}{ A_{2}} = \dfrac{r_{1}^{2}}{r_{2}^{2}} \end{array} \]Questo risultato è in contrasto con un teorema già noto ai greci (Elementi di Euclide – Libro XII, Proposizione 1): le aree di due poligoni regolari aventi lo stesso numero di lati stanno fra loro come i quadrati dei raggi dei cerchi circoscritti.
\[ P_{1}: P_{2} = r_{1}^{2}:r_{2}^{2} \]Quindi l’ipotesi che l’area \(A_{1}\) del cerchio sia troppo grande ha portato ad una contraddizione. Anche l’ipotesi opposta che l’area \(A_{1}\) sia troppo piccola è da scartare con lo stesso ragionamento (oppure basta scambiare il ruolo dei due cerchi).
In un articolo successivo descriveremo diverse applicazioni del metodo di esaustione, relative al calcolo di aree, lunghezze, volumi e superfici.
5) La teoria delle sezioni di Dedekind
Nel corso del secolo XIX sono stati definiti in modo rigoroso i concetti fondamentali dell’Analisi Matematica, in particolare il concetto di numero reale e il concetto di limite, che sono alla base del calcolo differenziale e integrale. Dedekind (1831-1916) diede una definizione rigorosa dei numeri razionali e dei numeri irrazionali, che insieme formano i numeri reali. Questo ha permesso di stabilire delle basi solide per l’analisi matematica, rendendola indipendente da qualsiasi considerazione geometrica.
Per definire i numeri irrazionali Dedekind partì dai numeri razionali e introdusse il concetto di sezione.
Definizione 5.1
Una partizione dei numeri razionali in due sottoinsiemi \(A,B\) non vuoti è una sezione se:
- \( A \cup B = \mathbb{Q}\) e \( A \cap B = \emptyset\)
- tutti gli elementi di \(A\) sono minori di tutti gli elementi di \(B\)
- l’insieme \(A\) non contiene un elemento maggiore di tutti gli altri
Indichiamo una sezione con il simbolo \((A,B)\).
Esempio 5.1
Ogni numero razionale \(x\) determina un’unica sezione di Dedekind. Ad esempio se \(x=2\) abbiamo:
Tuttavia esistono anche sezioni non generate da numeri razionali.
Esempio 5.2
Il numero irrazionale \(\sqrt{2}\) è definito dalla seguente sezione:
Quindi mediante il concetto di sezione possiamo rappresentare sia i numeri razionali sia i numeri irrazionali.
Si può dare una definizione equivalente utilizzando una sola classe, come propose il matematico inglese Bertrand Russel (1872-1970):
Definizione 5.2
Una sezione è un sottoinsieme \(L\) dei numeri razionali \(\mathbb{Q}\) tale che:
- \(L\ è non vuoto e \((\mathbb{Q}-L)\) è non vuoto
- \(L\) non contiene un elemento massimo
- per ogni \(x,y \in \mathbb{Q}\), se \(x \in L\) e \(y \lt x\) allora \(y \in L\)
Mediante questa definizione, una sezione di Dedekind consiste di tutti i numeri razionali a sinistra di un punto di divisione.
Ogni sezione di Dedekind rappresenta un numero reale.
Per quanto riguarda la continuità (o completezza) della retta reale, Dedekind propose il seguente assioma:
Assioma di continuità di Dedekind
Per ogni sezione \((A, B)\) esiste un solo elemento \(\alpha \in \mathbb{R}\) tale che
Il numero \(\alpha\) si chiama separatore della sezione \((A,B)\).
L’assioma di Dedekind (o di completezza) permette di porre in corrispondenza biunivoca i punti di una retta con gli elementi dell’insieme \(R\).
Ricordiamo che Dedekind usava la parola continuità, mentre oggi è comune il termine completezza. Si può dimostrare che l’assioma di Archimede in realtà è una conseguenza dell’assioma di Dedekind.
Sulle sezioni possiamo definire le \(4\) operazioni aritmetiche e stabilire le relazioni di ordinamento. In tal modo otteniamo degli oggetti che possiamo identificare con i numeri reali.
Esercizio 5.1 – Somma di due sezioni
Date due sezioni di Dedekind \(L,M\), la somma è così definita
Dimostrare che \(L+M\) è effettivamente una sezione di Dedekind.
Esercizio 5.2
Dimostrare che l’elemento zero per la somma è la sezione \(L=\{x \in \mathbb{Q}: x \lt 0\}\).
Un altro modo equivalente di definire i numeri reali è stato proposto da Cantor, mediante le successioni di Cauchy. L’idea base è che ogni numero reale è un il limite di una successione di numeri razionali.
Sui numeri reali è possibile definire una relazione di ordine. Nel seguito, con lo stesso simbolo \(\alpha\) intendiamo sia il numero reale sia l’insieme corrispondente alla sezione:
Definizione 5.3
Dati due numeri reali \(\alpha,\beta\), diciamo che \(\alpha\) è minore di \(\beta\) se la sezione corrispondente ad \(\alpha\) è contenuta nella sezione corrispondente a \(\beta\). Formalmente
Due numeri reali \(\alpha,\beta\) si dicono uguali se le due sezioni sono uguali come insiemi. Infine definiamo
\[ \begin{array}{l} \alpha \le \beta \iff \alpha \lt \beta \lor \alpha = \beta \\ \alpha \gt \beta \iff \beta \lt \alpha \\ \end{array} \]Si dimostra facilmente il seguente:
Teorema 5.1
Dati due numeri reali \(\alpha,\beta\), vale esattamente una delle tre seguenti relazioni:
6) Proprietà dei numeri reali
I numeri reali definiti mediante le sezioni di Dedekind o le successioni di Cantor sono la base sulla quale è costruita l’Analisi Matematica. Le principali proprietà dei numeri reali possono essere così suddivise:
- struttura algebrica
- ordinamento
- assiomi di completezza
6.1) Struttura algebrica
Per quanto riguarda la struttura algebrica, l’insieme \((\mathbb{R};+,\cdot)\) con le due operazioni di addizione e moltiplicazione è un campo algebrico. Questo significa che
6.2) Ordinamento
Con la relazione di ordine \( \le \) l’insieme dei numeri reali è un campo totalmente ordinato. Infatti è facile vedere che la relazione \(\le\) è una relazione di equivalenza, cioè riflessiva, simmetrica e transitiva. Inoltre, per tutti i numeri reali \(x,y,z\) si ha:
6.3) Completezza
Sia \(A\) un insieme di numeri reali. L’insieme \(A\) si dice limitato superiormente se esiste un limite superiore, cioè un numero reale \(K\) tale che \( x \le K, \forall x \in A\).
Definizione 6.1 – Estremo superiore
Sia \(A\) un insieme di numeri reali limitato superiormente. Un numero reale \(M\) si chiama estremo superiore di \(A\) se:
- \(x \le M, \quad \forall x \in A\)
- \(M \le K, \quad\) per ogni numero reale \(K\) che è un limite superiore di \(A\)
Dalle proprietà delle sezioni di Dedekind segue la completezza dei numeri reali, espressa mediante il seguente:
Teorema 6.1
Ogni insieme non vuoto \(S \subset \mathbb{R}\) limitato superiormente ha un estremo superiore contenuto in \(\mathbb{R}\).
Esercizio 6.1
Dimostrare che l’insieme dei numeri razionali \(\mathbb{Q}\) è un campo algebrico totalmente ordinato non completo.
Suggerimento
Utilizzare come insieme \(S\) il seguente:
S = \{x \in \mathbb{Q}: 0 \le x \le \sqrt{2}\} \subset{\mathbb{Q}}
\]
Per uno studio approfondito dei numeri reali e dei fondamenti della matematica vedere ad esempio [2].
7) Relazione della teoria di Eudosso con le sezioni di Dedekind
La teoria delle sezioni di Dedekind contiene molte idee della teoria delle proporzioni di Eudosso. Si può affermare con certezza che le moderne teorie dei numeri reali hanno origine nei concetti sviluppati oltre duemila anni prima da Eudosso.
In base alla teoria di Eudosso due numeri razionali \(\dfrac{a}{b}\) e \(\dfrac{c}{d}\) sono uguali se hanno la stessa relazione di ordine con tutti gli altri numeri razionali, cioè per ogni numero razionale \(x\) si ha:
La definizione di Eudosso è sostanzialmente equivalente alle sezioni di Dedekind, anche se Eudosso e i Greci ragionavano soltanto in termini di proporzioni e non avevano sviluppato il concetto di numero reale rappresentato da un insieme infinito.
Conclusione
La teoria delle proporzioni e il metodo di esaustione hanno permesso di superare la crisi dovuta alla scoperta dei numeri irrazionali e hanno fornito nuovi potenti strumenti per i matematici. Eudosso ha mostrato che ogni numero irrazionale può essere approssimato tramite numeri razionali, con qualsiasi grado di precisione.
Grazie alle sue teorie è stato possibile calcolare le aree e i volumi delle varie figure geometriche, pur senza avere a disposizione i metodi moderni del calcolo integrale, che verrà sviluppato in modo rigoroso da Newton e Leibniz nel secolo XVII.
Per i suoi contributi Eudosso merita di essere considerato uno dei più grandi matematici dell’antichità, insieme ad Euclide e Archimede.
Bibliografia
[1]T. Heath – A History of Greek Mathematics (Vol. I,II; Dover)
[2]J. Stillwell – The Real Numbers (Springer)

0 commenti