Il numero \(\pi\) è il rapporto fra la lunghezza della circonferenza di un cerchio e il suo diametro. Come è noto nella geometria euclidea tale rapporto è invariabile, qualunque siano le dimensioni del cerchio. Si tratta di un numero irrazionale, quindi con infinite cifre, il cui calcolo non è affatto immediato.
In questo articolo descriveremo il metodo proposto da Archimede (287–212 a.C.), uno dei più grandi matematici del mondo antico.
Per uno studio approfondito dell’opera di Archimede nei vari campi della matematica e della scienza si può vedere il testo di Heath [1].
1) Il calcolo di \(\pi\) prima di Archimede
I primi tentativi di calcolo del numero \(\pi\) vennero fatti dalle grandi civiltà del Medio Oriente. I Babilonesi utilizzarono l’approssimazione per difetto \(\pi \approx 3,125\), come risulta da una tavola risalente al periodo 1900-1700 a.C. I Babilonesi ottennero questo valore calcolando la lunghezza del perimetro di un esagono regolare inscritto nel cerchio, che è uguale a sei volte il raggio.
Gli antichi Egizi assegnarono a \(\pi\) un valore approssimato per eccesso. Dal famoso papiro di Rhind (prima del 1650 a.C.) risulta che essi calcolavano l’area del cerchio mediante la formula
dove \(D\) è il diametro.
Da questa formula si ricava il valore approssimato \(\pi \approx \dfrac{256}{81}=3,1605\).
Gli Egizi ottennero questo valore inscrivendo un cerchio in un quadrato con lato uguale a \(9\) unità. Quindi disegnarono una griglia \(3×3\) e un ottagono ottenuto con le diagonali dei \(4\) quadrati della griglia posti nei vertici del quadrato.
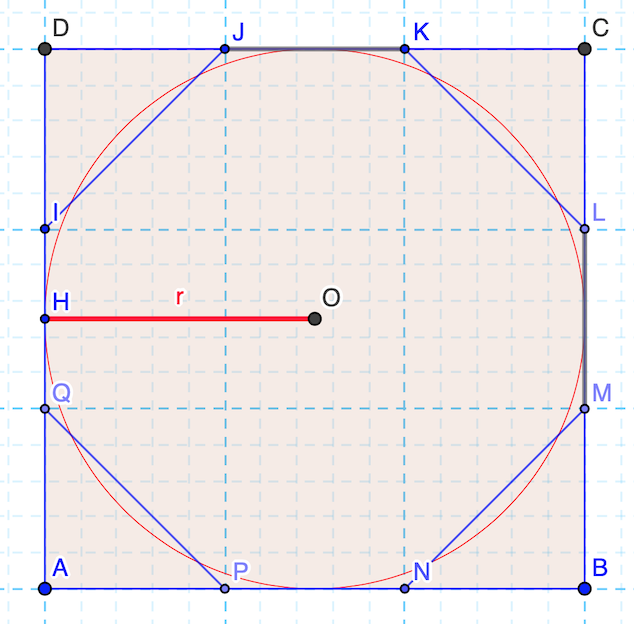
L’area del cerchio viene approssimata con l’area dell’ottagono, uguale a \(63\) unità, arrotondata al valore \(64=8^{2}\). Il valore approssimato di \(\pi\) è quindi
\[ \pi = \dfrac{4A}{D^{2}}=\dfrac{2^{8}}{3^{4}} \]Per la storia del numero \(\pi\) vedere il testo [2].
2) Il metodo di Archimede
Il procedimento di Archimede si basa sul metodo di esaustione, sviluppato dai Greci per il calcolo delle aree e dei volumi. Nel caso delle figure piane questo metodo consiste nella creazione di una successione di poligoni che convergono alla figura di cui si vuole calcolare l’area. Di fatto il metodo anticipa quelle che sarà il calcolo integrale sviluppato secoli più tardi da Newton, Leibniz e altri.
Uno dei risultati ottenuti da Archimede tramite il metodo di esaustione è la formula per il calcolo dell’area del cerchio.
Teorema 2.1 – Archimede
L’area di un cerchio è uguale all’area di un triangolo rettangolo la cui altezza è uguale al raggio del cerchio e la base è uguale alla lunghezza della circonferenza. In simboli abbiamo
Per una dimostrazione vedere il libro di Dunham [3].
Tuttavia rimaneva il problema di calcolare il valore della costante \(\pi\), cioè del rapporto fra la lunghezza della circonferenza e il diametro.
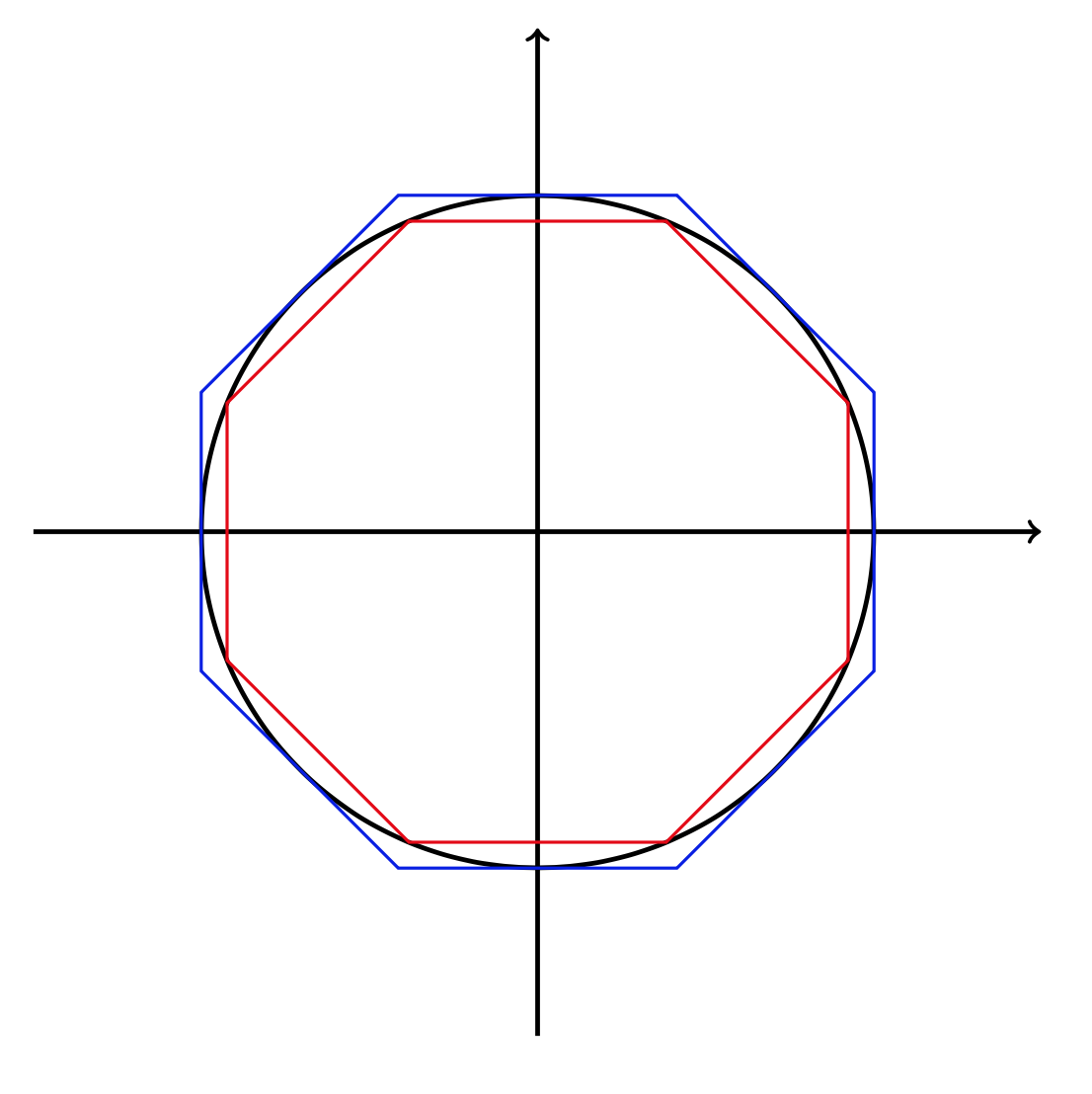
Archimede utilizzò il metodo di esaustione anche per determinare il valore approssimato di \(\pi\). L’idea di Archimede è di disegnare dei poligoni regolari inscritti e circoscritti al cerchio. Le lunghezze dei perimetri dei poligoni sono utilizzate per approssimare la lunghezza della circonferenza e quindi per calcolare il valore di \(\pi\). Chiaramente i poligoni circoscritti hanno lunghezze maggiori della circonferenza, mentre quelli inscritti hanno lunghezza minore. Tuttavia, aumentando il numero dei lati, i perimetri si avvicinano quanto si vuole alla lunghezza della circonferenza. In termini moderni possiamo dire che la lunghezza della circonferenza è il limite dei perimetri dei poligoni regolari, inscritti o circoscritti, al crescere del numero dei lati.
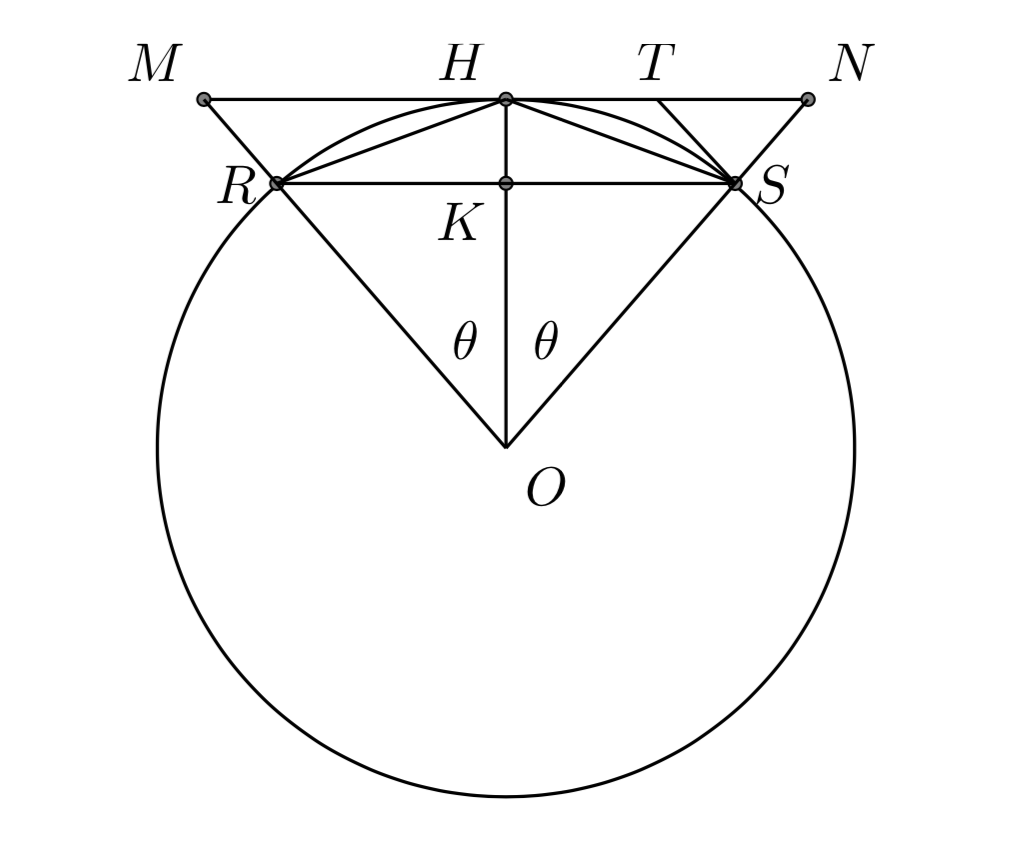
La figura seguente ci permette di capire come Archimede ricavò le equazioni ricorsive che permettono, in teoria, di calcolare il valore di \(\pi\) con il grado di approssimazione desiderato.
Nella figura sopra i segmenti \(RS\) e \(MN\) sono le lunghezze rispettivamente del poligono regolare di \(n\) lati inscritto e di quello circoscritto.
Poniamo \(RS=2s\) e \(MN=2t\). Il poligono regolare inscritto di \(2n\) lati ha lato di lunghezza \( HS=2\sigma\), mentre il poligono regolare circoscritto di \(2n\) lati ha il lato uguale al doppio di \(TS =\tau\).
I due triangoli \(TNS\) e \(NHO\) sono simili, quindi
Dalla due equazioni precedenti deriva subito
\[ \tau = \frac{ts}{t+s} \]I triangoli isosceli \(RHS\) e \(STH\) sono simili e quindi
\[ 2 \sigma^{2} = s \tau \]Il metodo di Archimede consiste nello scegliere due poligoni regolari iniziali di \(n\) lati, uno circoscritto e l’altro inscritto, con perimetri rispettivamente \(a_{n},b_{n}\). Quindi si raddoppia il numero dei lati, ottenendo i perimetri \(a_{2n},b_{2n}\). E così via.
Dalle formule precedenti si ricavano le formule iterative di Archimede:
Archimede scelse un esagono come poligono iniziale, ottenendo \(a_{6}=4\sqrt{3}R,b_{6}=6R\). A partire da questi valori si calcolano i successivi.
È facile dimostrare che la successione \(a_{n}\) è decrescente, mentre la successione \(b_{n}\) è crescente, ed entrambe convergono allo stesso limite, cioè alla lunghezza della circonferenza.
Esempio 2.1
Supponiamo di partire con un esagono regolare e raddoppiamo il numero dei lati. Se il cerchio ha raggio unitario otteniamo le seguenti approssimazioni per il valore di \(2\pi\):
Archimede eseguì l’algoritmo fino al passo \(5\), corrispondente ad un poligono regolare di \(96\) lati. Il valore ottenuto da Archimede per l’approssimazione di \(\pi\) è:
\[ 3,1408 \le \pi \le 3,1428 \]I valori calcolati da Archimede possono essere approssimati dai seguenti numeri razionali:
\[ \begin{array}{l} \dfrac{223}{71} \approx 3,1408 \\ \dfrac{22}{7} \approx 3,1428 \end{array} \]Esercizio 2.1
Con il metodo di induzione dimostrare le seguenti disuguaglianze:
3) Efficienza dell’algoritmo di Archimede
L’importanza del metodo di Archimede consiste nel fatto che per la prima volta è stato proposto un algoritmo iterativo in grado di calcolare il valore approssimato di \(\pi\). Tuttavia la convergenza dell’algoritmo è molto lenta.
Esercizio 3.1
Dimostrare che
Soluzione
Poniamo \(T(n)=\dfrac{b_{n}}{a_{n}+b_{n}}\). Ovviamente \(T(n) \lt \dfrac{1}{2}\) e quindi
Dalla relazione precedente ne deriva che le due successioni monotone convergono allo stesso limite. Poiché \(T(n) \to \dfrac{1}{2}\), ogni successiva iterazione aumenta la precisione di un fattore uguale a \(2\). Utilizzando il sistema di rappresentazione binario, possiamo dire che ogni iterazione aggiunge una cifra binaria all’approssimazione. Questo tipo di convergenza si chiama convergenza lineare. Questo significa che il numero delle cifre decimali corrette è approssimativamente direttamente proporzionale al numero delle iterazioni dell’algoritmo.
4) Calcolo di \(\pi\) dopo Archimede
Intorno all’anno \(150 \) d.C. Tolomeo utilizzò il metodo di Archimede, ottenendo il valore \(3,1416\).
In Cina il matematico Liu Hui, intorno al \(265\) d.C., con un metodo simile, utilizzando anche il teorema di Pitagora, riuscì a calcolare il numero \(\pi\) con \(4\) cifre decimali esatte. Successivamente il matematico cinese Zu Chongzhi (429–500 d.C.) riuscì ad ottenere la seguente approssimazione:
Questo risultato non venne migliorato per circa \(800\) anni. Agli inizi del \(1600\) il matematico tedesco Ludolph Van Ceulen riuscì a calcolare il numero \(\pi\) con \(35\) cifre decimali esatte. Il valore ottenuto è
\[ 3,14159265358979323846264338327950288 \cdots \]Questo numero viene anche chiamato numero ludolfiano.
5) Il metodo di Dörrie
Il matematico tedesco Heinrich Dörrie (1873-1955) ha proposto una modifica all’algoritmo di Archimede che permette di velocizzare la convergenza verso il valore esatto di \(\pi\).
Il procedimento di Dörrie utilizza la seguente disuguaglianza fra la media armonica e la media geometrica di due numeri:
Esercizio 5.1
Mediante la disuguaglianza precedente dimostrare le seguenti relazioni:
Poniamo ora:
\[ \begin{array}{l} A_{n}= \sqrt[3]{a_{n}b_{n}^{2}} \\ B_{n}= \dfrac{3a_{n}b_{n}}{2 a_{n}+ b_{n}} \\ \end{array} \]Esercizio 5.2
Dimostrare le seguenti relazioni:
Le successioni \(A_{n},B_{n}\) sono monotone e convergono alla lunghezza della circonferenza. Quindi
\[ B_{n} \lt 2\pi \lt A_{n} \\ \]Esempio 5.1
Calcolare con le formule di Dörrie le grandezze:
Come si può notare, il metodo di Dörrie calcola le prime due cifre decimali esatte di \(\pi\) già al primo passo con l’esagono, mentre l’algoritmo di Archimede richiede di effettuare \(5\) iterazioni, richiedendo un poligono regolare di \(96\) lati.
6) Moderni metodi per il calcolo di \(\pi\)
L’avvento di computer sempre più potenti e lo sviluppo di nuovi strumenti matematici hanno permesso di calcolare il valore di \(\pi\) con una precisione grandissima. Il numero di cifre decimali esatte ormai supera il trilione. I moderni metodi di calcolo rientrano in due principali categorie:
- serie infinite
- algoritmi iterativi
Una serie famosa, che converge molto rapidamente, è quella scoperta dal matematico indiano Ramanujan (1887-1920):
\[ \frac{1}{\pi}=\frac{\sqrt{8}}{9801}\sum\limits_{n=0}^{\infty}\frac{(4n)!}{(n!)^4}\frac{(26390n+1103)}{396^{4n}} \]Altre serie simili, ancora più veloci, sono state proposte dai fratelli Chudnovsky, due matematici americani di origine ucraina.
Naturalmente ci si può chiedere quale sia l’utilità pratica di calcolare un numero così grande di cifre decimali. Per gran parte dei settori della scienza e della tecnologia basta un piccolo numero di cifre decimali. Anche nei calcoli più complessi della fisica o dell’astronomia l’utilità di avere più di \(15\) cifre decimali è pressoché nulla.
L’unica applicazione concreta in cui può essere utile conoscere un numero elevato di cifre decimali può essere quella di utilizzare le cifre per effettuare i test dei computer e dei chip elettronici, per evidenziare eventuali errori di fabbricazione.
Tuttavia l’interesse dei matematici non è di natura applicativa, ma teorica. L’obiettivo principale è analizzare le cifre decimali per scoprire le proprietà della loro distribuzione.
Definizione 6.1
Un numero reale si dice normale se, nella sua espansione in cifre rispetto ad una base intera \(b \gt 1\), ognuna delle cifre appare con una frequenza che tende al valore \(\dfrac{1}{b}\). Se questa proprietà vale per ogni base \(b=2,3,\cdots\), allora si dice assolutamente normale.
Sostanzialmente in un numero normale ogni sequenza di cifre ha la stessa probabilità di apparire nello sviluppo.
Nonostante le cifre decimali di \(\pi\) si avvicino alla distribuzione uniforme con grande approssimazione, al momento non si è ancora in grado di stabilire se \(\pi\) è un numero normale oppure no.
Per una panoramica dei moderni metodi di calcolo vedere il testo [4].
Conclusione
Il numero \(\pi\) ha un posto speciale nella matematica, nella scienza e nella cultura umana in generale. Nonostante i progressi fatti, i matematici continueranno a studiare il numero \(\pi\) e le sue cifre decimali. La conoscenza di un numero sempre maggiore di cifre decimali forse potrà far emergere delle proprietà interessanti ancora nascoste.
Il nome di Archimede resterà per sempre associato al numero \(\pi\). Anche se oggi si utilizzano altri metodi più sofisticati e potenti, resta il grande merito di Archimede di aver sviluppato per primo un processo iterativo che, in teoria, permette di calcolare il valore approssimato di \(\pi\) con il grado di precisione desiderato.
Bibliografia
[1]T. Heath – The Works of Archimedes (Dover)
[2]P. Beckmann – A History of Pi (St Martin’s Press)
[3]W. Dunham – Journey Through Genius: The Great Theorems of Mathematics (Penguin)
[4]D. Bailey, J. Borwein – Pi: The Next Generation: A Sourcebook on the Recent History of Pi and its Computation (Springer)



0 commenti