L’entropia è un concetto fondamentale, nato con lo studio delle leggi della termodinamica e poi esteso a molti campi della scienza, tra cui la biologia, l’economia, i sistemi complessi e la teoria dell’informazione elaborata da Shannon nel 1948.
In questo articolo introdurremo il concetto di entropia nel contesto del calcolo delle probabilità e la distribuzione di variabili aleatorie.
1) Le varie interpretazioni del concetto di entropia
L’entropia è un concetto che può esser applicato in diversi campi della scienza. Vediamo in seguito i più significativi.
1.1) Entropia e Fisica
La nascita del concetto di entropia può esser fatta risalire al secolo XIX, con lo studio delle leggi della termodinamica. In particolare Rudolf Clausius (1822-1888) cercava di stabilire le leggi che regolano lo scambio di calore fra corpi aventi temperature diverse. Come è noto il calore si trasferisce naturalmente dai corpi più caldi a quelli più freddi. L’entropia è il concetto sviluppato per spiegare questo comportamento; letteralmente entropia significa “misura del disordine”. Gli studi di Clausius e altri portarono a stabilire la seconda legge della termodinamica, che ha vari enunciati equivalenti, tra i quali i seguenti:
- L’entropia di un sistema isolato tende ad aumentare nel tempo, fino a raggiungere l’equilibrio termico.
- È impossibile realizzare una trasformazione fisica il cui unico risultato sia quello di trasferire calore da un corpo più freddo a uno più caldo, senza utilizzare del lavoro esterno.
Il secondo principio della termodinamica è una delle leggi fondamentali della fisica. Applicata all’universo intero, la legge afferma che il livello di disordine nell’universo è destinato ad aumentare in modo irreversibile, passando da un sistema ordinato ad un sistema sempre più disordinato.
Un altro scienziato, Ludwig Boltzmann (1844-1906), cercò di spiegare il comportamento macroscopico dei sistemi fisici a partire dai componenti elementari, le molecole e gli atomi. In particolare spiegò il secondo principio della termodinamica come risultato del movimento caotico delle particelle elementari. Ogni corpo macroscopico è costituito da un numero grandissimo di molecole e atomi. Secondo Boltzmann l’entropia è strettamente collegata con la distribuzione delle varie configurazioni microscopiche possibili. L’entropia tende ad assumere un valore massimo in corrispondenza della configurazione che ha la massima probabilità termodinamica. In termini matematici questo è espresso mediante la famosa legge di Boltzmann:
dove \(S\) è l’entropia, e \(W\) è il numero delle configurazioni possibili, mentre \(k\) è una costante chiamata costante di Boltzmann.
All’aumentare del numero di stati possibili diminuisce l’informazione sullo stato del sistema, e quindi aumenta l’entropia. L’entropia è una grandezza fondamentale per spiegare i processi fisici e biologici, e anche per simulare la possibile evoluzione del nostro universo. Per un approfondimento di questi temi vedere [1].
1.2) Entropia e probabilità
L’entropia è strettamente collegata al calcolo delle probabilità. Ad esempio supponiamo di lanciare \(10\) monete; la probabilità che escano tutte testa o tutte croci è piccola, mentre è più probabile che escano \(5\) teste e \(5\) croci. Le configurazioni di \(10\) teste o \(10\) croci sono più ordinate, e quindi hanno minore entropia delle configurazioni con \(5\) teste e \(5\) croci.
Un altro esempio è dato da un mazzo di carte: quando mischiamo le carte sostanzialmente aumentiamo l’entropia, che raggiunge il massimo valore quando ognuna delle \(52\) permutazioni delle carte è ugualmente probabile. Un mazzo nuovo, in cui le carte sono ordinate per seme e numero, ha un valore basso dell’entropia e un alto grado di ordinamento.
1.3) Entropia e Teoria dell’Informazione
Il concetto di entropia ha un ruolo fondamentale nella moderna teoria dell’informazione, nata nel 1948 con la pubblicazione del libro di Claude Shannon (1916 – 2001) “A Mathematical Theory of Communication”.
L’informazione può essere definita a partire da una variabile che può assumere diversi valori, e che viene memorizzata o trasmessa. Otteniamo informazione quando siamo in grado di conoscere il valore del contenuto della variabile. Possiamo definire l’entropia di una variabile come la quantità di informazione contenuta nella variabile stessa. La quantità di informazione non dipende tanto dalla lunghezza del contenuto, ma dalla sorpresa che suscita in noi leggendo il contenuto. Ovviamente in questo senso l’entropia, come la probabilità, è un concetto relativo, che dipende dallo stato di conoscenza che ha il soggetto.
Nella teoria dell’informazione di Shannon l’entropia è strettamente collegata all’informazione. Maggiore è l’incertezza sul contenuto di una variabile o sul verificarsi di un evento, maggiore è l’informazione che riceviamo.
2) L’informazione associata ad un evento casuale
Abbiamo visto che l’informazione misura il grado di sorpresa nel verificarsi di un evento aleatorio (o casuale). Supponiamo di aver un mazzo di 40 carte napoletane. Mischiando in modo causale sono possibili \(40!\) disposizioni, un numero enorme. La probabilità dell’uscita di una particolare disposizione è quindi \(p=\dfrac{1}{40!}\). Poiché l’informazione è inversamente proporzionale alla probabilità, a questo evento possiamo assegnare un contenuto informativo uguale a \(\dfrac{1}{p}\). Per comodità di calcolo si usa una scala logaritmica. In genere si utilizzano i logaritmi in base \(2\), poiché in informatica si utilizzano i bit per codificare e memorizzare le informazioni. Tuttavia si potrebbe utilizzare qualunque altra base \(b \gt 1\). Come è noto i logaritmi espressi un due basi diverse differiscono per una costante, in base alla seguente formula:
\[ \log_{a}x = \dfrac{\log_{b}x}{\log_{b}a} \]L’informazione associata alla notizia che si è verificato un evento è così definita:
Definizione 2.1
L’informazione associata ad un evento \(E\) con con probabilità \(p=P(E)\) è la seguente:
Naturalmente l’informazione \(I(p)\) è un numero non negativo, in quanto \(0 \le p \le 1\).
Se utilizziamo i logaritmi in base \(2\) l’unità di misura dell’informazione è il bit. Un bit rappresenta la quantità di informazione nel caso in cui si ha uguale probabilità di scelta fra due alternative, ad esempio nel lancio di una moneta non truccata. Il bit rappresenta la quantità minima di informazione misurabile. Non si deve confondere la misura dell’informazione con il numero di bit necessari per codificare un messaggio.
Esempio 2.1
Supponiamo di lanciare una moneta non truccata. Definiamo gli eventi \(A = \{\text{testa}\}\), \(B=\{\text{croce}\}\) e supponiamo che \(P(A)=P(B)=\dfrac{1}{2}\). L’informazione che si ottiene conoscendo il risultato del lancio è quindi:
La funzione \(I(p)\) è definita nell’intervallo \((0,1]\), ed è chiaramente una funzione continua: a due eventi che hanno una piccola differenza di probabilità devono corrispondere due informazioni o sorprese che differiscono di poco tra loro. Inoltre la funzione \(I(p)\) ha le seguenti proprietà caratteristiche:
\[ \begin{array}{l} I(1) = 0 \quad \text{nessuna sorpresa} \\ I(p) \ge 0 \quad p \in (0,1] \\ I(p) \gt I(q) \quad \text{se} \quad p \lt q \\ I(pq) = I(p) + I(q) \quad \forall p,q \\ \end{array} \]La quarta proprietà afferma che l’informazione associata a due eventi indipendenti è uguale alla somma delle informazioni dei singoli eventi. In termini matematici supponiamo di avere due eventi \(A,B\), e indichiamo con \(P(A\cap B)\) la probabilità che entrambi gli eventi si verifichino. Allora, se gli eventi sono indipendenti, l’informazione associata è:
\[ I(P(A \cap B)) = I(P(A)P(B)) = \ – \log_{2}(P(A)P(B))= \ – \log_{2}P(A) – \log_{2}P(B) = I(P(A)) + I(P(B)) \]Vale il seguente teorema:
Teorema 2.1
Sia data una funzione continua \(I(p) : (0,1] \to \mathbb{R}\). Se la funzione soddisfa le quattro proprietà precedenti allora è della forma
dove \(K\) è un numero reale positivo arbitrario.
Dimostrazione
Applicando il metodo di induzione e sfruttando le proprietà della funzione \(I(p)\), si dimostrano facilmente le seguenti relazioni:
Dalle relazioni precedenti si deduce che deve essere \(I(p^{x})=xI(p)\) per ogni numero reale positivo \(x\). Ora, in base alla definizione del logaritmo è possibile scrivere \(p=\left(\dfrac{1}{2}\right)^{-\log_{2}(p)}\) e quindi, applicando la formula precedente con \(x=-\log_{2}(p)\), abbiamo
\[ I(p)=- I\left(\dfrac{1}{2}\right)\log_{2}(p)=-K \log_{2}(p) \]con \(K=I\left(\dfrac{1}{2}\right)\). La costante \(K\) è positiva.
Esempio 2.2
Supponiamo di lanciare un dado non truccato. Lo spazio campionario dei risultati possibili è \(X=\{1,2,3,4,5,6\}\). Ogni evento ha probabilità \(p=\dfrac{1}{6}\). Quindi l’informazione relativa al risultato di un singolo lancio è
Esercizio 2.1
Se due eventi \(A,B\) non sono indipendenti, dimostrare che
dove \(P(B|A)\) è la probabilità condizionata che si verifichi l’evento \(B\), se è noto che si è verificato l’evento \(A\).
3) L’entropia di un sistema completo di eventi casuali
Un sistema completo di eventi su uno spazio di probabilità è un insieme finito di eventi incompatibili fra loro \(A=\{A_{1},A_{2},\cdots,A_{n}\}\) tali che
\[ \sum\limits_{k=1}^{n}P(A_{k})=1 \]Ad esempio, nel lancio di un dado abbiamo \(6\) eventi possibili corrispondenti alle facce del dado, mentre nel lancio di due dadi abbiamo \(36\) eventi possibili, corrispondenti alle coppie di risultati dei due dadi.
Definizione 3.1
L’entropia \(H\) di un sistema completo di eventi è definita nel modo seguente:
In questo caso l’entropia rappresenta l’informazione ricevuta conoscendo quale fra gli eventi \(A_{1},A_{2},\cdots,A_{n}\) si è verificato in una certa prova.
Nella formula si deve intendere che
La formula può essere estesa al caso \(n= \infty\).
Notiamo che la funzione \(H(p_{1},p_{2}, \cdots,p_{n})\) assume sempre valori positivi, tranne nel caso in cui una delle probabilità \(p_{i}=1\) e tutte le altre sono uguali a zero. In altri termini se uno degli eventi è certo e gli altri sono impossibili, allora non c’è alcuna incertezza e quindi l’entropia è nulla.
Il valore massimo assunto dalla funzione \(H(p_{1},p_{2}, \cdots,p_{n})\) è indicato nel seguente teorema:
Teorema 3.1
La funzione \(H(p_{1},p_{2}, \cdots,p_{n})\) assume il valore massimo nel caso di eventi equiprobabili, cioè \(p_{k}=\dfrac{1}{n},k=1,2,\cdots,n\).
Dimostrazione
\[ \log_{2}n – H=\sum\limits_{k=1}^{n}p_{k}\log_{2} (np_{k})\ge \frac{1}{\ln 2}\sum\limits_{k=1}^{n}p_{k}\left(1-\frac{1}{np_{k}}\right)=0 \\ \]dove abbiamo utilizzato la disuguaglianza \(\ln x \ge (1-\frac{1}{x}), (x \gt 0)\), dove il simbolo \(\ln x\) indica il logaritmo naturale, che ha come base il numero di Eulero \(e \approx 2,718\). Quindi abbiamo
\[ H=-\sum\limits_{k=1}^{n}p_{k}\log_{2} p_{k}\le \log_{2}n \\ \]Chiaramente se \(np_{k}=1, k=1,2, \cdots,n\), allora l’entropia raggiunge il massimo valore: \(H=\log_{2} n\).
Esempio 3.1
Supponiamo di lanciare due dadi non truccati. Lo spazio campionario dei risultati possibili è costituito dalle \(36\) coppie \((x,y)\), con \(x,y=1,2,3,4,5,6\). Ogni coppia ha probabilità \(p=\dfrac{1}{36}\). Quindi l’informazione relativa al risultato di un singolo lancio è
Dati due schemi di eventi \(A=\{A_{1},A_{2},\cdots,A_{n}\}\) e \(B=\{B_{1},B_{2},\cdots,B_{m}\}\), possiamo definire lo schema prodotto
\[ AB = \{A_{i}B_{j}, i=1,2,\cdots,n; j=1,2,\cdots,m\} \]Se gli schemi sono indipendenti la probabilità di un evento congiunto è \(P(A_{i}B_{j})= P(A_{i})P(B_{j})\).
Il teorema di unicità
Riportiamo ora il teorema di unicità di Shannon-Khinchin, il quale afferma che l’espressione della funzione \(H(p_{1}, \cdots,p_{n})\) sopra riportata è l’unica che soddisfa le proprietà dell’entropia. Ricapitoliamo le proprietà principali della funzione entropia \(H(p_{1},p_{2}, \cdots, p_{n})\):
- \(H(AB) = H(A) + H(B)\) dove \(A,B\) sono due schemi indipendenti
- la funzione \( H(p_{1},p_{2}, \cdots,p_{n})\) assume il valore massimo nel caso in cui gli \(n\) eventi sono equiprobabili, cioè \(p_{k}=\dfrac{1}{n},k=1,2,\cdots,n\)
- \(H(p_{1},p_{2}, \cdots,p_{n},0)= H(p_{1},p_{2}, \cdots,p_{n})\)
L’ultima condizione implica che, aggiungendo un evento di probabilità, nulla non si produce alcun effetto sul grado di incertezza e quindi sull’entropia di un sistema di eventi.
Teorema 3.2 – Shannon-Khinchin
Sia \(H(p_{1},p_{2}, \cdots, p_{n})\) una funzione definita per ogni intero positivo \(n\) e numeri reali \(p_{k} \ge 0\) tali che \(\sum\limits_{k=1}^{n}p_{k}=1\). Se la funzione è continua rispetto alle \(n\) variabili e verifica le tre proprietà dell’elenco precedente, allora ha la seguente espressione:
dove \(\lambda\) è un numero reale positivo. Per semplicità si pone \(\lambda = 1\).
Per una dimostrazione vedere [2].
4) Entropia di una variabile aleatoria
Come è noto una variabile aleatoria \(X\) è una funzione definita su uno spazio campionario \(\Omega\), che associa un numero reale \(x\) ad ogni evento elementare \(\omega\):
\[ \begin{array}{l} X: \Omega \to \mathbb{R} \\ X (\omega)=x \\ \end{array} \]Una variabile aleatoria si dice discreta se l’insieme dei valori assunti è finito o numerabile, altrimenti si dice continua.
Esempio 4.1 – Variabile di Bernoulli
Supponiamo di lanciare una moneta. In questo caso lo spazio campionario è \(\Omega=\{\text{testa,croce}\}\). La variabile di Bernoulli è così definita:
4.1) Entropia di una variabile aleatoria discreta
Data una variabile aleatoria discreta \(X\), che assume i valori \(x_{1},x_{2}, \cdots, x_{n}\) con rispettive probabilità \(p_{1},p_{2}, \cdots, p_{n}\), l’entropia è così definita:
\[ H(X)= -\sum\limits_{k=1}^{n}p_{k}\log_{2}p_{k} \]La definizione si estende anche al caso \(n=\infty\).
Esempio 4.1
Sia data una variabile aleatoria di Bernoulli \(X\) che assume i valori \(1,0\) con probabilità \(p,1-p\) rispettivamente. L’entropia è
Il diagramma sottostante illustra l’andamento del valore dell’entropia al variare di \(p\).
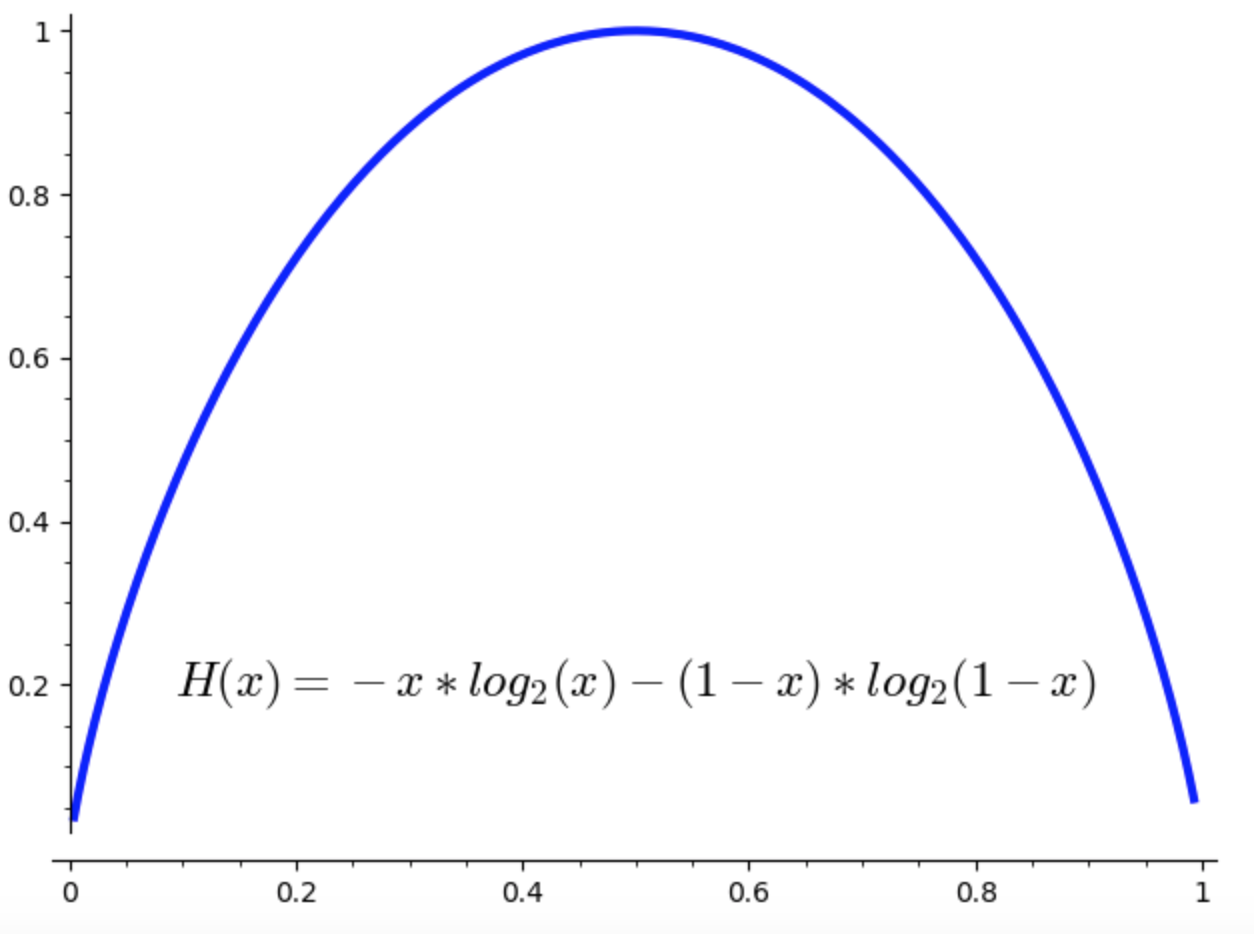
Esercizio 4.1
Supponiamo di avere due monete: la probabilità che esca testa vale \(\dfrac{1}{2}\) per la prima moneta, e \(\dfrac{2}{3}\) per la seconda moneta. Lanciamo la prima moneta due volte e la seconda tre volte.
Determinare quale dei due risultati ha maggiore certezza?
Soluzione
Denotiamo con \(X\) la variabile aleatoria che indica il numero di volte nelle quali esce testa con la prima moneta. La distribuzione è quella binomiale:
Nel nostro caso per la prima moneta abbiamo \(n=2\), \(p=\dfrac{1}{2}\), \(k=0,1,2\). L’entropia corrispondente è
\[ H_{1}= -\frac{1}{4}\ln \frac{1}{4} – \frac{1}{2}\ln \frac{1}{2} – \frac{1}{4}\ln \frac{1}{4} \]In modo analogo si procede per la seconda moneta, trovando l’entropia
\[ H_{2}= -\frac{1}{27}\ln \frac{1}{27} – \frac{2}{9}\ln \frac{2}{9} – \frac{4}{9}\ln \frac{4}{9} – \frac{8}{27}\ln \frac{8}{27} \]Facendo i calcoli si trova che il lancio della prima moneta ha minore entropia, e quindi maggiore certezza.
4.2) Entropia di una variabile aleatoria continua
Una variabile aleatoria continua può assumere un insieme continuo di valori. Esempi sono il tempo di arrivo di un treno ad una stazione, la posizione di un punto scelto a caso in un intervallo, ecc.
Come è noto una variabile aleatoria continua è descritta da una funzione \(f(x)\) definita sulla retta reale \([-\infty,+\infty]\), chiamata densità di probabilità, che ha queste proprietà:
Per calcolare la probabilità che la variabile aleatoria \(X\) assuma un valore compreso in un intervallo \([a,b]\), vale la formula seguente:
\[ P(a \le X \le b)= \int\limits_{a}^{b}f(x)dx \\ \]Data una variabile aleatoria continua \(X\), che ha una funzione densità di probabilità \(f(x)\), l’entropia è così definita:
\[ H[X]= -\int\limits_{-\infty}^{\infty}f(x)\log_{2}f(x) dx \]Teorema 4.1
Fra tutte le variabili aleatorie che hanno una data varianza \(\sigma^{2}\), la distribuzione normale di Gauss è quella cha ha la massima entropia.
Dimostrazione
Il problema consiste nel determinare il massimo degli integrali del seguente tipo
con le seguenti condizioni:
\[ \begin{array}{l} \int\limits_{-\infty}^{\infty}f(x)dx = 1 \\ \int\limits_{-\infty}^{\infty}(x -\overline{x})^{2}f(x)dx = \sigma^{2} \\\end{array} \]dove il simbolo \(\overline{x}\) denota il valore medio della variabile aleatoria.
Si possono utilizzare le equazioni di Eulero-Lagrange del calcolo delle variazioni per risolvere il problema. Bisogna trovare il massimo della seguente funzione ausiliaria:
In questo caso l’equazione di Eulero-Lagrange è la seguente:
\[ – \ln f(x) -1 + \lambda_{1} + \lambda_{2}(x-\overline{x})^{2}=0 \]Risolvendo abbiamo
\[ f(x) = K e^{- \lambda_{2}(x-\overline{x})^{2}} \]Tenendo conto dei vincoli del problema possiamo calcolare il valore della costante \(K\), ottenendo come soluzione di massima entropia proprio la distribuzione normale di Gauss:
\[ f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{- \dfrac{(x-\overline{x})^{2}}{2\sigma^{2}}} \]Esercizio 4.2
Determinare la distribuzione di probabilità con massima entropia, fra tutte variabili aleatorie continue la cui densità di probabilità si annulla al di fuori di un intervallo finito \([a,b]\).
Soluzione
Utilizzando lo stesso metodo del teorema precedente si trova che la distribuzione con entropia massima è quella uniforme:
Esercizio 4.3
Determinare la distribuzione di probabilità con massima entropia, fra tutte variabili aleatorie continue la cui densità di probabilità si annulla per \(x \lt 0\).
Soluzione
Procedendo in modo simile si trova che la distribuzione con entropia massima è quella esponenziale:
5) Entropia di due variabili aleatorie
Definizione 5.1
Date due variabili aleatorie discrete \(X,Y\), l’entropia congiunta è così definita:
dove \(p(x,y)=P(X=x,Y=y)\) è la densità congiunta di probabilità delle due variabili aleatorie. L’entropia congiunta misura l’incertezza sulle due variabili aleatorie prese insieme. Si può facilmente dimostrare il seguente teorema:
Teorema 5.1
Se due variabili aleatorie \(X,Y\) sono indipendenti, allora
Per la dimostrazione basta applicare la definizione e ricordare che \(p(x,y)=p(x)p(y)\) se le due variabile aleatorie sono indipendenti.
Un problema importante è calcolare l’informazione ricevuta osservando una variabile aleatoria \(X\), se si conosce il valore di un’altra variabile aleatoria \(Y\).
Definizione 5.2
L’entropia condizionata di una variabile aleatoria discreta \(X\) rispetto ad una variabile aleatoria discreta \(Y\) che assume il valore \(Y=y\) è così definita:
Se il valore della variabile \(Y\) non è noto dobbiamo fare la media sull’insieme dei valori possibili. In questo caso abbiamo quindi
\[ H(X|Y)= -\sum\limits_{x \in X}\sum\limits_{y \in Y} p(x,y) \log_{2}p(x|y) \]Nel caso continuo abbiamo formule analoghe, con le somme sostituite da integrali. Ad esempio
\[ H(X|Y=y)= -\int\limits_{-\infty}^{\infty}f(x|y)\log_{2}f(x|y) dx \]dove \(f(x|y)\) è la densità di probabilità condizionata.
L’entropia condizionata \(H(X|Y)\) rappresenta la quantità di informazione relativa ad \(X\) dovuta al verificarsi di \(Y\).
Esercizio 5.1
Dimostrare che \(H(X|Y) \le H(X)\).
In altri termini, la conoscenza di \(Y\) riduce il valore dell’entropia o al massimo lo lascia invariato.
Esercizio 5.2
Dimostrare che se \(X,Y\) sono indipendenti allora \(H(X|Y)=H(X)\).
Esercizio 5.3
Dimostrare che in generale
Definizione 5.3
L’informazione mutua \(I(X;Y)\) fra due variabili aleatorie \(X,Y\) è così definita:
Rappresenta la riduzione dell’incertezza di \(X\), a causa della conoscenza di \(Y\). Chiaramente \(I(X;Y)=0\) se e solo se le due variabili aleatorie sono indipendenti.
Esercizio 5.4
Dimostrare le seguenti proprietà dell’informazione mutua:
6) Applicazioni
6.1) La disuguaglianza di Fano (1871-1952)
Prima di introdurre la disuguaglianza di Fano, ricordiamo il concetto di supporto di una variabile aleatoria.
Definizione 6.1
Data una variabile aleatoria discreta \(X\), il supporto \(R_{X}\) è l’insieme dei valori che la variabile aleatoria può assumere con probabilità maggiore di zero:
Per una variabile aleatoria continua con densità di probabilità \(f_{X}(x)\), il supporto è il seguente:
\[ R_{X}=\{ x \in \mathbb{R}| f_{X}(x) \gt 0\} \]Esempio 6.1
\[ f_{X}(x) = \begin{cases} 1 \quad x \in [0,1] \\ 0 \quad \text{altrimenti} \\ \end{cases} \]In questo caso \(R_{X}=[0,1]\).
Supponiamo di conoscere il valore di una variabile aleatoria \(Y\) e di voler stimare il valore di un’altra variabile aleatoria \(X\). Se la variabile \(X\) è una funzione della \(Y\) allora l’entropia condizionata \(H(X|Y)\) è uguale a zero e in questo caso possiamo stimare \(X\) con probabilità di errore uguale a zero. Possiamo affermare in generale che se \(H(X|Y)\) ha un valore piccolo, allora anche la probabilità di commettere errore nella stima di \(X\) è piccola.
Supponiamo ora che \(p(x)\) sia la la densità di probabilità della variabile aleatoria \(X\), e \(p(x|y)\) sia la densità condizionata di \(X\) dato che si conosce \(Y\). Il problema consiste nella stima della variabile aleatoria \(X\), a partire da risultati relativi ad osservazioni sulla variabile \(Y\). Definiamo con il simbolo \(\overline{X}\) la variabile aleatoria che assume i valori della nostra stima.
Definiamo la variabile aleatoria \(E\):
Ricordiamo anche che l’entropia associata alla variabile aleatoria \(E\) è
\[ H(E) = -p_{e}\log_{2}(p_{e})-(1-p_{e})\log_{2}(1-p_{e}) \]dove \(p_{e}=P(E=1)\), rappresenta la probabilità di commettere un errore nella stima.
Stabiliamo ora una regola di decisione: per ogni valore \(y_{i}\) della variabile aleatoria \(Y\) stimiamo che il valore della variabile \(X\) sia \(x_{i^{*}}\):
La probabilità media di fare una stima corretta è:
\[ p_{c}=\sum\limits_{i}{}P(Y=y_{i})P(X=x_{i^{*}}|Y=y_{i}) \]La probabilità di errore è quindi \(p_{e}=1-p_{c}\).
Teorema 6.1 – Fano
\[ H(E) + p_{e}\log_{2}(|R_{X}|-1) \ge H(X|Y) \]Notiamo che se \(p_{e}=0\), allora \(H(E)=0\) e quindi deve essere \(H(X|Y)=0\).
Dal teorema deriva la seguente relazione:
e anche la seguente
\[ p_{e} \ge \frac{H(X|Y) -1 }{\log_{2}|R_{X}|} \]Per una una dimostrazione vedere [3].
La disuguaglianza di Fano dice che se \(H(X|Y)\) è grande, cioè se, dato il verificarsi di \(Y\), la variabile aleatoria \(X\) ha una grande incertezza, allora qualunque stima di \(X\) basata su \(Y\) ha una grande probabilità di errore.
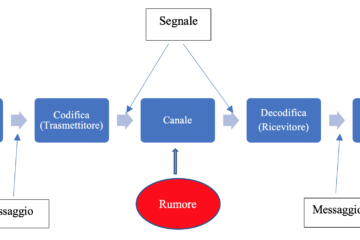
Un esempio di applicazione è dato dalla Teoria dell’Informazione: indichiamo con \(X\) il simbolo trasmesso da una sorgente, scelto da un insieme finito di simboli possibili, mentre indichiamo con \(Y\) il simbolo ricevuto da un destinatario. In presenza di errori sul canale di comunicazione la formula di Fano fornisce una stima dell’errore di decodifica del simbolo inviato. L’entropia condizionata rappresenta il rumore presente nel canale di trasmissione.
Esempio 6.2 – Caso binario
Se la v.a. \(X\) è binaria, allora \(|R_{X}|=2\) e quindi
La disuguaglianza di Fano ha importanti applicazioni in vari campi: Teoria dell’informazione, Inferenza statistica, Teoria delle decisioni e altri.
6.2) L’entropia dei numeri naturali
Come è noto, il teorema fondamentale dell’aritmetica afferma che ogni numero naturale \(n\) può essere espresso in modo univoco come prodotto di un numero finito di potenze di numeri primi:
\[ n = p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{k}^{a_{k}} \]L’esponente \(a_{i}\) si chiama molteplicità del numero primo \(p_{i}\). Nella teoria dei numeri la somma delle molteplicità viene indicata con la seguente funzione \(\Omega(n)\):
\[ \Omega(n)=a_{1}+ a_{2}+ \cdots + a_{k} \]Il numero dei fattori primi distinti viene invece indicato con la funzione \(\omega(n)\):
\[ \omega(n)=\sum\limits_{p|n}1 \]Possiamo definire la frequenza \(f_{i}\) di un numero primo \(p_{i}\) nella fattorizzazione di \(n\) nel seguente modo:
\[ f_{i}= \dfrac{a_{i}}{\Omega(n)}=\dfrac{a_{i}}{a_{1}+ a_{2}+ \cdots + a_{k}} \]Come è noto, un modo classico di definire la probabilità di un evento è di fare un numero grande di prove e calcolare il rapporto fra il numero dei successi e il numero delle prove, cioè la frequenza dei successi. Questo legame della frequenza con la probabilità suggerisce di poter applicare il concetto di entropia anche ai numeri naturali e alla loro scomposizione in prodotto di numeri primi. Ad ogni numero primo \(p_{i}\) della fattorizzazione possiamo associare una probabilità in base alla sua molteplicità:
\[ p(a_{i})= \dfrac{a_{i}}{\Omega(n)} \]Naturalmente \(\sum\limits_{i=1}^{k}p(a_{i})=1\). Possiamo quindi considerare i numeri \(p(a_{i})\) come valori assunti dalla seguente variabile aleatoria discreta:
\[ X(n)=\{p(a_{1}), p(a_{2}), \cdots, p(a_{k})\} \\ \]Definizione 6.2
L’entropia del numero \(n=p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{k}^{a_{k}}\) è la seguente:
Esercizio 6.1
Dimostrare che \(H(p^{k})=0\).
Si possono dare anche altre definizioni di entropia di un numero naturale. Una è la seguente:
\[ H(n) = k \ln p(n) \]dove \(p(n)\) è la funzione di partizione di Eulero (vedi link).
Un’altra definizione possibile è legata al teorema dei numeri primi:
Prendendo spunto dalla formula di Boltzmann possiamo definire la seguente formula per l’entropia \(S(x)\) di un intero positivo:
\[ S(x) = \dfrac{x}{\pi (x)} \]L’entropia di un intero positivo \(x\) è quindi uguale al rapporto fra l’intero stesso e la funzione \(\pi(x)\), che conta il numero dei primi minori od uguali a \(x\).
7) Entropia e sistemi complessi
Come abbiamo visto l’entropia è una misura del disordine in un sistema: l’entropia aumenta se il disordine aumenta. Le cause dell’aumento del disordine possono essere forze interne o esterne che tendono a far evolvere il sistema verso uno stato disordinato.
Il concetto di entropia è fondamentale nello studio della Teoria Generale dei Sistemi. Un sistema può essere definito come un insieme di elementi che interagiscono fra loro. Per uno studio approfondito vedere il testo classico di von Bertalanffy[4] (1901-1972). I sistemi possono essere di vario tipo:
- sistemi biologici (ad esempio una cellula umana, un animale, un uomo, ecc.)
- sistemi artificiali e tecnologici prodotti dall’uomo
- organizzazioni di varia natura
Lo studio di von Bertalanffy era concentrato sui sistemi biologici, considerati come sistemi aperti. L’entropia dei sistemi biologici può diminuire, raggiungendo alti livelli di organizzazione, prendendo energia dall’ambiente esterno, nel quale l’entropia aumenta.
In generale nei sistemi artificiali, come ad esempio nei grandi sistemi informativi, l’entropia tende ad aumentare: il disegno iniziale strutturato evolve verso uno stato di maggiore disordine, a causa dei continui cambiamenti durante il ciclo di vita del sistema, compromettendo l’integrità strutturale iniziale. L’aumento di entropia tuttavia può essere contenuto se la manutenzione viene fatta correttamente.
7.1) Entropia e il Web
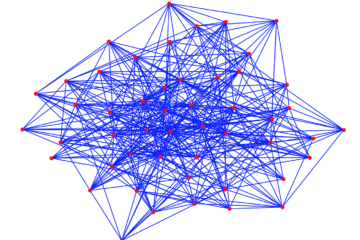
L’entropia è un concetto utile anche per studiare le prestazioni della rete Internet, un sistema costituito da miliardi di siti web. La struttura del Web può essere rappresentata con un grafo: i vertici del grafo sono le pagine e gli archi sono i collegamenti (hyperlink). Per comprendere la rete Internet è necessario conoscere la disposizione dei nodi, i collegamenti e la dinamica dei flussi di informazioni che vengono trasmessi lungo la rete nel tempo.
Lo studio dell’entropia del sistema Internet è complesso e richiede strumenti matematici avanzati e metodi sofisticati di raccolta delle informazioni sul traffico. Non esiste un’unica definizione per l’entropia della rete Internet; alcuni si concentrano sulla distribuzione dei nodi e delle relative connessioni, altri sui collegamenti e sui flussi di informazione fra i vari nodi.
L’accesso alle informazioni presenti sui vari siti web è reso possibile grazie all’architettura del DNS (Domain Name System). Il DNS è un database distribuito e gerarchico, che permette un’associazione fra i nomi simbolici dei siti web (hostname) e gli indirizzi IP. È sostanzialmente una specie di elenco telefonico, che traduce il nome del sito web (es. www.ibm.com) in un indirizzo IP (es. \(64.233.160.0)\). L’indirizzo IP permette di accedere al server sul quale risiede il sito web.
La struttura reticolare e il grande numero di collegamenti alternativi fornisce alla rete Internet un grande grado di resilienza, cioè di resistenza e capacità di adattarsi alle mutevoli situazioni.
7.2) Entropia e sicurezza della rete Internet
Ogni computer collegato alla rete Internet di fatto è connesso con milioni di altri computer. Questo espone ad attacchi informatici di vario tipo: furto di informazioni riservate, modifica di dati, blocco degli accessi, ecc.
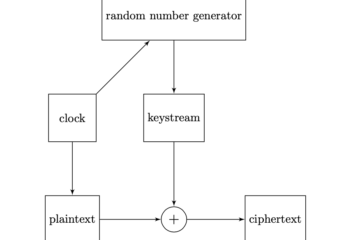
La crittografia è uno strumento fondamentale per assicurare l’integrità dei dati, la riservatezza delle informazioni e l’accesso controllato ai sistemi web. L’entropia è fondamentale per creare algoritmi crittografici efficienti e sicuri. Ad esempio una misura della qualità di un algoritmo crittografico è rappresentata dall’entropia degli output della funzione di hashing.
Un altro aspetto importante della sicurezza è rappresentato dalla difesa contro gli attacchi esterni e interni, virus, trojan e impedimento del servizio (DDoS – Distributed Denial of Service). Gli attacchi DDoS consistono nell’inviare un numero grande di richieste su un sito, fino a renderlo inservibile, in quanto viene saturata la banda di comunicazione. Per individuare gli attacchi DDoS è utile analizzare il traffico sulla rete Internet; le variazioni di entropia rispetto a valori medi spesso sono un indizio di presenza di attacchi DDoS.
L’entropia può essere utilizzata anche per individuare i diversi tipi di flussi nella rete. Possiamo misurare l’entropia in base al numero di byte per pacchetto trasferiti sulla rete nel corso del tempo. Un valore alto dell’entropia implica che sulla rete sono trasmessi dati di vario tipo e dimensioni: testi, audio, immagini, video. Un valore basso potrebbe essere un indizio della presenza di malware, che sta intasando la rete, con un flusso di dati ripetuti.
Conclusione
In questo articolo abbiamo esaminato le proprietà generali dell’entropia, le sue connessioni con il calcolo delle probabilità e l’informazione relativa ad eventi aleatori.
Nei prossimi articoli studieremo in dettaglio la Teoria dell’Informazione, inizialmente sviluppata da Shannon e poi ampliata da altri studiosi. La Teoria dell’Informazione è alla base dei componenti della moderna società digitale: reti di computer, internet, DVD, telefonini, televisioni ad alta definizione, ecc. Inoltre ha un ruolo fondamentale nella scienza della crittografia e della trasmissione sicura dei dati, un’esigenza imprescindibile nell’era delle reti di computer e di Internet.
Bibliografia
[1]S. Carroll – From Eternity to Here: The Quest for the Ultimate Theory of Time (Dutton)
[2]A. Y. Khinchin – Mathematical Foundations of Information Theory (Dover)
[3]T. M. Cover and J. A. Thomas – Elements of Information Theory (John Wiley & Sons)
[4]Ludwig von Bertalanffy – General System Theory (George Braziller Inc.)
0 commenti