La Legge di Reciprocità Quadratica di Gauss

La legge di reciprocità quadratica ha un ruolo centrale nella teoria dei numeri. Venne inizialmente formulata da Eulero mentre studiava le proprietà dei numeri primi della forma \(x^{2}+ ny^{2}\). Anche Legendre diede importanti contributi. Il teorema venne dimostrato in modo completo per la prima volta da Gauss nel 1796. La fonte principale per lo studio dei residui quadratici e della legge di reciprocità quadratica rimane la fondamentale opera di Gauss ‘Disquisitiones Arithmeticae’, pubblicata nel 1801 in latino. È un libro straordinario per i contenuti e per la chiarezza di esposizione. Rimane una delle opere più importanti della matematica che pone le fondamenta teoriche della moderna teoria dei numeri. Per la versione in inglese vedere ^[1].
Gli argomenti illustrati in questo articolo possono essere approfonditi in questi testi classici: ^[2], ^[3].

---

1) L’Aritmetica Modulare di Gauss

Dato un intero positivo \(m\), si dice che due interi \(a\) e \(b\) sono congruenti modulo \(m\) se danno lo stesso resto nella divisione per \(m\). Si usa la seguente notazione introdotta da Gauss:

\[ a \equiv b \pmod{m} \]

Per un ripasso delle proprietà delle congruenze lineari vedere l’articolo di questo blog.
Ricordiamo ora alcune proprietà che saranno utilizzate in seguito.

Teorema 1.1 (Bézout)
Siano dati due interi \(a,b\). Se \((a,b)=d\) allora esistono interi \(x_{0},y_{0}\) tali che

\[ d=ax_{0}+ by_{0} \]

Questa proprietà deriva direttamente dall’algoritmo di divisione di Euclide, che si studia nell’aritmetica di base. Per una dimostrazione vedere uno dei testi indicati nella bibliografia.

Teorema 1.2
Se \((a,m)=1\) allora esiste un intero \(x\) tale che \(ax \equiv 1 \pmod m\). Se \((a,m) >1\) non esiste alcuna soluzione.

Dimostrazione
Utilizzare il teorema precedente.

Definizione 1.1
Ricordiamo che si chiama sistema completo di residui \(\pmod{m}\) un insieme di interi \(X\) tale che ogni altro intero \(k \in \mathbf{Z}\) è congruente ad uno degli elementi di \(X\). Per ogni \(m\) l’insieme \(\{0,1,2, \cdots ,m-1\}\) è un sistema completo di residui \(\pmod {m}\).
In alcuni problemi è conveniente scegliere un sistema completo di residui minimo in valore assoluto.
Se \(m\) è dispari il sistema di residui minimo in valore assoluto è il seguente: \(X= \{-\frac{m-1}{2}, -\frac{m-3}{2}, \cdots , -1,0,1, \cdots, \frac{m-3}{2}, \frac{m-1}{2}\}\).
Se \(m\) è pari esistono due sistemi completi di residui minimi in valore assoluto: \(X_{1}= \{-\frac{m-2}{2}, \cdots , -1,0,1, \cdots, \frac{m-2}{2}, \frac{m}{2}\}\), \(X_{2}= \{-\frac{m}{2},-\frac{m-2}{2},\cdots , -1,0,1, \cdots, \frac{m-2}{2}\}\).

Ad esempio, se \(m = 6\), allora:
\(X_{1} = \{-2,-1,0,1,2,3\}\) e \(X_{2} = \{-3,-2,-1,0,1,2\}\).

Definizione 1.2
Dato un intero positivo \(m\), sappiamo che esistono \(\varphi(m)\) interi primi con \(m\), dove \(\varphi(m)\) è la funzione di Eulero (vedi link). Si chiama sistema ridotto di residui \(\pmod{m}\) un insieme di interi \(X^{*}\) primi con \(m\) tale che ogni intero \(a \in \mathbf{Z}\) con \((a,m)=1\) è congruente ad uno e uno solo degli elementi di \(X^{*}\).

Esercizio 1.1
Sia \(\{a_{1},a_{2}, \cdots ,a_{\varphi(m)}\}\) un sistema ridotto di residui \(\mod{m}\). Dimostrare che se b è un intero tale che \((b,m)=1\), allora anche l’insieme \(\{ba_{1},ba_{2}, \cdots , ba_{\varphi(m)} \}\) è un sistema ridotto di residui.

Ricordiamo inoltre una proprietà fondamentale dei numeri primi, dimostrata da Euclide:

Teorema 1.3 (Euclide)
Se \(p\) è un numero primo e \(p |ab\) allora \(p|a\) oppure \(p|b\).

Per la dimostrazione si può usare il teorema 1.1 di Bézout.

Teorema 1.4
La congruenza \(x^{2} \equiv 1 \pmod{p}\) ha soluzioni se e solo se \(x \equiv \pm 1 \pmod{p}\)

Dimostrazione
Se vale la congruenza allora \((x-1)(x+1)\equiv 0 \pmod{p}\). Per il teorema 1.3 deve essere \(p|(x-1)\) oppure \(p|(x+1)\), e quindi \(x\equiv 1 \pmod{p}\) oppure \(x\equiv -1 \pmod{p}\). Il viceversa è ovvio.

---

2) I residui quadratici

Consideriamo ora l’insieme \(X\) dei numeri \(\{x,2x, \cdots , (p-1)x \}\) con \(1 \le x \le p-1\). I numeri dell’insieme sono tutti incongruenti fra loro \(\pmod p\) e quindi, se \((a,p)=1\) allora \(a\) è congruente ad uno solo dei numeri dell’insieme. Possiamo concludere che la congruenza \(xy \equiv a \pmod p\) ammette una ed una sola soluzione \( 0 < y < p\). Possiamo chiamare i due numeri \(x,y\) associati fra loro. Sono possibili due casi distinti:

2.1) Primo caso: nessun numero \(x\) è associato con se stesso

In questo caso, se nessun \(x\) è associato con se stesso, diciamo che \(a\) è un non-residuo quadratico modulo \(p\). Poiché la congruenza \(x^{2} \equiv a \pmod p\) non ha soluzioni, possiamo raggruppare i numeri da \(1\) a \(p-1\) in \(\frac{p-1}{2}\) coppie di associati, ottenendo il seguente risultato:

\[ \prod_{1 \le x \le p-1}x= (p-1)! \equiv a^{\frac{p-1}{2}} \pmod p \]

2.2) Secondo caso: esiste un numero \(x\) associato con se stesso

Se invece esiste un \(x_{1}\) che è associato con se stesso allora \(x_{1}^{2} \equiv a \pmod p\) e diciamo che \(a\) è un residuo quadratico modulo \(p\). Per ogni soluzione della congruenza ne esiste un’unica altra data da \(z_{1} = p-x_{1} \equiv -x_{1} \pmod p\). Ovviamente si ha \( x_{1} z_{1} \equiv -a \pmod p\). Non esistono altre soluzioni della congruenza, come è facile verificare. Possiamo quindi raggruppare i numeri da \(1\) a \(p-1\) nella coppia \((x_{1},z_{1})\) e in altre \(\frac{p-3}{2}\) coppie di associati distinti, ottenendo il seguente risultato:

\[ \prod_{1 \le x \le p-1}x= (p-1)! \equiv -a^{\frac{p-1}{2}} \pmod{p} \]

Nota
Ovviamente tutti i numeri sono residui quadratici \(\pmod{2}\). Per questo d’ora in poi, salvo avviso contrario, assumeremo che sia sempre \(p\) dispari.
Possiamo quindi dare la seguente definizione:

Definizione 2.1
Sia \(p\) un primo dispari. Un numero intero \(a\) si dice che è un residuo quadratico \(\pmod {p}\), e si scrive \(aRp\), se esiste una soluzione della congruenza

\[ x^{2} \equiv a \pmod{p} \]

Se invece non esiste una soluzione della congruenza, allora \(a\) si dice che è un non-residuo quadratico, e si scrive \(aNp\).
Per indicare i residui si usa il simbolo di Legendre, introdotto nel 1798:

\[ \begin{split} \left(\frac{n}{p}\right) = \left\{ \begin{array}{rl} 1 & \mbox{se } n \mbox{ a è un residuo quadratico mod } p\\ -1 & \mbox{se } n \mbox{ a è un non-residuo quadratico mod } p \\ 0 & \mbox{se } p|n. \end{array} \right. \end{split} \]

In base alle considerazioni fatte all’inizio del paragrafo possiamo enunciare il seguente teorema:

Teorema 2.1
Se \(p\) è un primo dispari e \((a,p)=1\) allora:

\[ (p-1)! \equiv -\left(\frac{a}{p}\right) a^{\frac{p-1}{2}} \pmod{p} \]

Vediamo ora altre proprietà importanti dei residui quadratici e del simbolo di Legendre.

Teorema 2.2
Supponiamo che \(p\) sia un primo dispari. Allora esistono \(\frac{p-1}{2}\) residui quadratici \(\pmod{p}\) e lo stesso numero di non-residui quadratici.

Dimostrazione
Consideriamo l’insieme \(X = \{ a^{2}: a=1,2, \cdots , \frac{p-1}{2}\}\). L’insieme \(X\) contiene tutti i residui quadratici, in quanto vale la seguente relazione:

\[ (p-a)^{2} \equiv a^{2} \pmod{p} \]

Inoltre i numeri dell’insieme \(X\) sono tutti diversi \(\pmod{p}\), come è facile verificare.

Esercizio 2.1
Calcolare tutti i residui quadratici di \(11\).

Soluzione
Abbiamo \(1^{2} \equiv 1 \pmod{11}\), \(5^{2} \equiv 3 \pmod{11}\), \(9^{2} \equiv 4 \pmod{11}\), \(4^{2} \equiv 5 \pmod{11}\), \(3^{2} \equiv 9 \pmod{11}\). Quindi i residui sono \((1,3,4,5,9)\), mentre i non-residui sono \((2,6,7,8,10)\).

Teorema 2.3
Supponiamo che \(p\) sia un primo dispari e \((a,p)=(b,p)=1\). Allora il prodotto \(ab\) è un residuo quadratico \(\pmod{p}\) se e solo se \(a,b\) sono entrambi residui quadratici oppure entrambi non-residui quadratici.

Dimostrazione
Supponiamo che \(a\) sia un residuo quadratico. Se \(b\) assume tutti i valori non nulli di residui \(\pmod{p}\), lo stesso fa il prodotto \(ab\), essendo \((a,p)=1\).
Ora se \(b\) è un residuo quadratico, allora chiaramente lo è anche il prodotto \(ab\). D’altra parte sappiamo che i residui quadratici sono in numero di \(\frac{p-1}{2}\), e quindi il prodotto \(ab\) deve essere un non-residuo quadratico se \(b\) è un non-residuo quadratico.
Con un ragionamento simile si dimostra il teorema se \(a\) è un non-residuo quadratico.

Dal teorema precedente deriva la seguente regola del prodotto:

Teorema 2.4

\[ \left(\frac{mn}{p}\right) = \left(\frac{m}{p}\right)\left(\frac{n}{p}\right) \]

Esercizio 2.2
Dimostrare che \(\left(\frac{1}{p}\right)=1\)

---

3) Il teorema di Wilson e il criterio di Eulero

Teorema 3.1 (Wilson)
Se \(p\) è un numero primo allora:

\[ (p-1)! +1 \equiv 0 \pmod{p} \]

Il teorema di Wilson deriva direttamente dal teorema 2.1, ponendo \(a=1\). Tuttavia è interessante dare una dimostrazione combinatoria dello stesso teorema.

Sia dato quindi un numero \(p\) dispari. Consideriamo un cerchio diviso in \(p\) archi di uguale lunghezza. Il numero di poligoni stellati che possiamo costruire mediante questi vertici è \(\frac{p!}{2p}\). Possiamo suddividere i poligoni stellati in due gruppi. Il primo gruppo contiene i poligoni che rimangono invariati ruotando di un angolo uguale a \(\frac{2 \pi}{p}\) radianti. Questo gruppo contiene \(\frac{p-1}{2}\) poligoni. I rimanenti \(\frac{p!}{2p}-\frac{p-1}{2}\) possono essere raggruppati in gruppi ognuno di \(p\) elementi. Ogni elemento di un gruppo è ottenuto da un altro mediante successive rotazioni di \(\frac{2 \pi}{p}\). Quindi il numero totale dei gruppi di poligoni è:

\[ \frac {\frac{p!}{2p}-\frac{p-1}{2}}{p}= \frac{(p-1)!-(p-1)}{2p} \]

Poiché il risultato deve essere intero si ha: \(2p|((p-1)! -p+1)\) e quindi \(p|(p-1)!+1\).

Teoricamente il teorema di Wilson potrebbe essere utilizzato come criterio per determinare se un numero è primo, in quanto la congruenza non vale nel caso di un numero composto \(m\). Infatti se \(m=ab\), con \( 1 < a < m\), allora \(a\) non può dividere \((m-1)!+1\). Tuttavia come criterio non è utilizzabile per numeri grandi.

Esercizio 3.1
Dimostrare che se \(m\) è composto e diverso da \(4\) allora risulta \((m-1)! \equiv 0 \pmod{m}\).

Esercizio 3.2
Mediante il teorema di Wilson dimostrare la seguente proprietà dei coefficienti binomiali:

\[ \binom{p-1}{k} \equiv (-1)^{k} \pmod{p} \]

Teorema 3.2
La congruenza \(x^{2} \equiv -1 \pmod {p}\) ha soluzioni se e solo se \(p=2\) oppure \(p \equiv 1 \pmod{4}\)

Dimostrazione
Se \(p=2\) allora \(x= 1\). Supponiamo \(p\) dispari. Per il teorema di Wilson si ha:

\[ (p-1)! = \prod_{k=1}^{\frac{p-1}{2}}k(p-k) \equiv -1 \pmod{p} \]

Ora \(k(p-k) \equiv -k^{2} \pmod{p}\) e quindi

\[ (-1)^{\frac{p-1}{2}}(\prod_{k=1}^{\frac{p-1}{2}}k)^{2} \equiv -1 \pmod{p} \]

Da questo troviamo la soluzione \(x=(\frac{p-1}{2})!\) se \(p=4j+1\).
Viceversa supponiamo che \(x^{2} \equiv -1 \pmod{p}\). Eleviamo alla potenza \(\frac{p-1}{2}\) troviamo

\[ (-1)^{\frac{p-1}{2}} \equiv (x^{2})^{\frac{p-1}{2}}\equiv x^{p-1} \pmod{p} \equiv 1 \pmod{p} \]

per il piccolo teorema di Fermat. Da questo ne deduciamo che deve essere \((-1)^{\frac{p-1}{2}}=1\), cioè \(p=4j+1 \equiv 1 \pmod{4}\).

Dal teorema 2.1 deriva subito il seguente:

Teorema 3.3

\[ \left(\frac{-1}{p}\right)=(-1)^{\frac{p-1}{2}} \]

Quindi \(-1\) è un residuo quadratico rispetto ai primi della forma \(4k+1\) e un non-residuo quadratico rispetto ai primi della forma \(4k+3\).

Dal teorema 2.1 deriva anche il seguente generale criterio di Eulero:

Teorema 3.4 – Criterio di Eulero

\[ \left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}} \pmod{p} \]

---

4) La Legge di reciprocità quadratica di Gauss

Ricordiamo la definizione di sistema completo di residui minimo in valore assoluto, data all’inizio di questo articolo. Se \(p\) è un primo dispari, esiste esattamente un solo residuo di un intero \( n \pmod{p}\) compreso fra \(\frac{-p}{2}\) e \(\frac{p}{2}\).

Teorema 4.1 (Lemma di GAUSS)
Sia \(p\) un primo dispari e sia \((a,p)=1\). Sia \(X\) l’insieme \( \{1 \cdot a, 2 \cdot a,3 \cdot a, \cdots, \frac{p-1}{2} \cdot a\}\). Sia \(S\) il sistema completo di residui minimo in valore assoluto modulo \(p\) dei numeri di \(X\). Se \(n\) indica il numero degli elementi di \(S\) che sono negativi, allora vale la seguente relazione:

\[ \left(\frac{a}{p}\right)=(-1)^{n} \]

Dimostrazione
Indichiamo con \(s_{1},s_{2}, \cdots , s_{m}\) e \(r_{1},r_{2}, \cdots, r_{n}\) rispettivamente gli elementi positivi inferiori a \(\frac{p}{2}\) e gli elementi maggiori di \(\frac{p}{2}\). Nel sistema completo di residui minimo in valore assoluto al posto degli elementi \(r_{j}\) abbiamo gli elementi negativi \(t_{j}=r_{j}-p\).
Ovviamente gli elementi \(s_{i}\) sono tutti distinti e lo stesso vale per gli elementi \(t_{i}\). Inoltre se un elemento \(s_{i}\) fosse uguale in valore assoluto ad un elemento \(t_{j}\), allora si avrebbe \(ak \equiv s_{i} \pmod{p}\) e \(ah \equiv -t_{j} \pmod{p}\), e quindi \(a(k+h) \equiv 0 \pmod{p}\). Ma questo non è possibile poiché \(0<k+h< p\).
Possiamo quindi concludere che i numeri \(s_{i},-t_{j}\) sono tutti i numeri positivi dell’insieme \(\{1,2, \cdots, \frac{p-1}{2}\}\) in un certo ordine. Quindi

\[ a\cdot 2a \cdots \frac{p-1}{2}a= (-1)^{n}\left(\frac{p-1}{2}\right)! \pmod{p} \]

Semplificando e applicando il criterio di Eulero abbiamo infine:

\[ a^{\frac{p-1}{2}} \equiv \left(\frac{a}{p}\right)\pmod{p} \equiv (-1)^{n} \pmod{p} \]

Teorema 4.2
Dimostrare la seguente formula:

\[ \left(\frac{2}{p}\right)=(-1)^{\frac{p^{2}-1}{8}} \]

Soluzione
Utilizziamo il lemma di Gauss. Contiamo il numero dei residui nell’intervallo \((-\frac{p}{2},\frac{p}{2})\) dei numeri \(2,4, \cdots , p-1\), con segno negativo.Condizione necessaria e sufficiente per generare un numero negativo è che si abbia \(2k > \frac{p-1}{2}\), e quindi \(k > \frac{p-1}{4}\). Possiamo dire quindi che il valore dell’esponente del lemma di Gauss è

\[ n = \frac{p-1}{2}- \left\lfloor \frac{p}{4} \right\rfloor \]

• se \(p \equiv 1 \pmod{4}\) allora \(n =\frac{p-1}{4}= \lfloor \frac{p+1}{4} \rfloor\)
• se \(p \equiv 3 \pmod{4}\) allora \(n =\frac{p+1}{4}= \lfloor \frac{p+1}{4} \rfloor\)

Quindi

\[ \left(\frac{2}{p}\right) \equiv (2)^{\frac{p-1}{2}} \equiv (-1)^{ \left\lfloor \frac{p+1}{4} \right\rfloor } \]

La formula precedente è equivalente alle seguenti:

\[ \left(\frac{2}{p}\right) = \begin{cases} 1 \text{ se \(p=8k+1\) oppure \(p=8k-1\)}\\ -1 \text{ se \(p=8k+3\) oppure \(p=8k-3\)}\\ \end{cases} \]

Osserviamo ora che la quantità \(\frac{p^{2}-1}{8}\) è pari se \(p=8k \pm 1\), mentre è dispari se \(p=8k \pm 3\). Quindi il teorema è dimostrato.
Il seguente teorema è utilizzato nella dimostrazione della legge di reciprocità quadratica.

Teorema 4.3
Se \(p\) è un primo dispari e \((a,p)=1\) allora l’esponente \(n\) del lemma di Gauss è:

\[ n \equiv \sum_{k=1}^{\frac{p-1}{2}} \left \lfloor \frac{ka}{p}\right\rfloor \pmod{2} \]

Dimostrazione
Utilizziamo le notazioni del lemma di Gauss. Consideriamo i resti di valore assoluto minimo ottenuti dividendo gli interi \(ka\) per \(p\), con \(k=1,2, \cdots, \frac{p-1}{2}\). I quozienti delle divisioni sono \(q=\left\lfloor \frac{ka}{p}\right\rfloor\). Quindi se \((a,p)=1\) abbiamo:

\[ \sum_{k=1}^{\frac{p-1}{2}} ka =\sum_{k=1}^{\frac{p-1}{2}}p \left\lfloor \frac{ka}{p}\right\rfloor + \sum_{k=1}^{n} s_{k} + \sum_{k=1}^{m}r_{k} \]

Ricordando che \(n+m= \frac{p-1}{2}\), con semplici passaggi otteniamo

\[ (a-1)\sum_{k=1}^{\frac{p-1}{2}}k = p(\sum_{k=1}^{\frac{p-1}{2}}\left\lfloor \frac{ka}{p}\right\rfloor-n) + 2 \sum_{k=1}^{n} r_{k} \]

Da questa segue

\[ (a-1)\frac{p^{2}-1}{8} \equiv \sum_{k=1}^{\frac{p-1}{2}}{\left\lfloor \frac{ka}{p} \right\rfloor} – n \pmod{2} \]

Se \(a\) è dispari ne segue che \(n \equiv \sum_{k=1}^{\frac{p-1}{2}} {\lfloor\frac{ka}{p}\rfloor} \pmod{2}\). Se \(a=2\) allora \(\lfloor \frac{2k}{p}\rfloor=0\) per \(1 \le k \le \frac{p-1}{2}\), e quindi ritroviamo il risultato del teorema 4.2.

Teorema 4.4
Dati due numeri primi dispari distinti \(p,q\) allora:

\[ \sum_{k=1}^{\frac{p-1}{2}}\left\lfloor \frac{kq}{p}\right\rfloor +\sum_{k=1}^{\frac{q-1}{2}}\left\lfloor \frac{kp}{q}\right\rfloor = \frac{p-1}{2} \frac{q-1}{2} \]

Dimostrazione
Consideriamo la funzione \(F(x,y)=qx-py\). Se \(x\) assume i valori \(1,2, \cdots, \frac{p-1}{2}\) e \(y\) assume i valori \(1,2, \cdots, \frac{q-1}{2}\), allora la funzione \(F(x,y)\) assume un numero totale di \(\frac{p-1}{2}\frac{q-1}{2}\) valori diversi e non nulli. Fissato un \(x\), i valori sono positivi se e solo se \(y \le \lfloor \frac{qx}{p}\rfloor\) . Quindi il numero totale dei valori positivi è:

\[ \sum_{k=1}^{\frac{p-1}{2}}\left\lfloor \frac{qk}{p}\right\rfloor \]

Una formula analoga vale per i valori negativi. Quindi il teorema è dimostrato, in quanto il numero totale dei valori assunti è \(\frac{p-1}{2}\frac{q-1}{2}\).

Il teorema precedente ha una interessante interpretazione geometrica, illustrata dal seguente grafico:

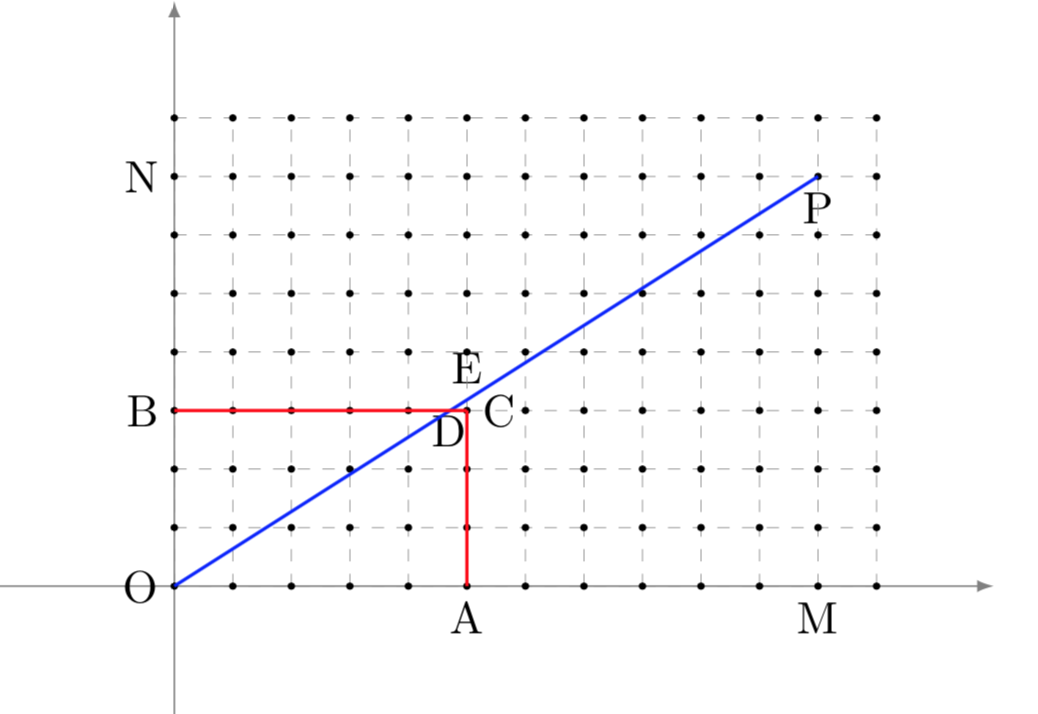
Definiamo \(S(p,q)=\sum_{k=1}^{\frac{p-1}{2}}\lfloor \frac{kq}{p}\rfloor \). La somma \(S(p,q)+S(q,p)\) è uguale al numero dei punti interi (cioè con coordinate intere), escludendo i punti sugli assi, contenuti nel rettangolo OACB con vertici \(\{(0,0);(\frac{p-1}{2},0);(\frac{p-1}{2},\frac{q-1}{2});(0,\frac{q-1}{2})\}\). Nel grafico \(p=11\) e \(q=7\).
La prima somma conta i punti interi nel triangolo \(OAE\); la seconda quelli nel triangolo \(OBD\). Per i dettagli vedere il testo di Hardy-Wright.

Teorema 4.5 – Legge di reciprocità quadratica
Siano \(p,q\) due primi dispari distinti. Allora

\[ \left(\frac{p}{q}\right) \left(\frac{q}{p} \right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}} \]

Dimostrazione
In base al Teorema 4.3 e al lemma di Gauss:

\[ \begin{split} \left (\frac{q}{p} \right) &= (-1)^{m} \\ m & \equiv \sum_{k=1}^{\frac{p-1}{2}}\left\lfloor \frac{qk}{p}\right\rfloor \pmod{2} \\ \end{split} \]

In modo analogo

\[ \begin{split} \left (\frac{p}{q}\right) &= (-1)^{n} \\ n & \equiv \sum_{k=1}^{\frac{q-1}{2}}\left\lfloor \frac{pk}{q}\right\rfloor \pmod{2} \\ \end{split} \]

Quindi \(\left (\frac{p}{q}\right) \left (\frac{q}{p}\right)=(-1)^{m+n}\) e il teorema di reciprocità segue dal teorema 4.4).

Nota
Gauss rimase molto affascinato dalla bellezza di questo teorema, che chiamò il ‘Theorema Aureum’ o anche la “Gemma dell’Aritmetica”. Gauss presentò almeno otto diverse dimostrazioni. In seguito vennero fornite moltissime altre dimostrazioni di questo importante teorema (vedere il seguente link).

Esercizio 4.1
Calcolare il valore di \(\left(\frac{15}{47}\right) \)

\[ \begin{split} \left(\frac{15}{47}\right) &= \left(\frac{3}{47}\right) \left(\frac{5}{47}\right) =(-1) \left(\frac{47}{3}\right) \left(\frac{47}{5}\right) \\ &= (-1) \left(\frac{-1}{3}\right) \left(\frac{2}{5}\right) = \left(\frac{2}{5}\right) = -1 \\ \end{split} \]

Esercizio 4.2
Determinare tutti i primi dispari per i quali il numero \(5\) è un residuo quadratico, cioè \(\left (\frac{5}{p}\right) = 1\).

Soluzione
In questo caso abbiamo:

\[ \left(\frac{5}{p}\right) \left(\frac{p}{5}\right) = (-1)^{\frac{p-1}{2}\frac{5-1}{2}}=1 \]

Quindi \(\left (\frac{5}{p}\right) = 1\) se e solo se risulta \( \left (\frac{p}{5}\right) = 1\). Ma la congruenza \(x^{2} \equiv p \pmod{5}\) ha soluzione se e solo se \(p \equiv \pm 1 \pmod{5}\).

Un altro utilizzo della legge di reciprocità quadratica è il calcolo del simbolo di Legendre per numeri molto grandi.

Esercizio 4.3
Dimostrare che \(\lfloor \frac{611}{1009}\rfloor=1\)

Traccia
Osservare che \(611=13 \cdot 47\) e \(1009\) è un numero primo.

---

5) Teoremi di Fermat sulla somma di due quadrati

Teorema 5.1
Un numero primo \(p\) dispari può essere espresso come somma di due quadrati se e solo se è della forma \(p \equiv 1 \pmod{4}\). In simboli

\[ p=x^{2} + y^{2} \text{ se e solo se \(p=4k+1\) } \]

Dimostrazione
Intanto se \(p=x^{2} + y^{2}\) è dispari, allora \(x,y\) hanno parità diverse e quindi è chiaramente vero che \(p=4k+1\). Viceversa supponiamo che \(p=4k+1\). In questo caso sappiamo che \(\left( \frac{-1}{p}\right)=1\) e quindi esiste un intero \(t\) tale che \(t^{2} \equiv -1 \pmod{p}\). Consideriamo ora l’insieme dei numeri \(X=\{at+b; 0 \le a,b \le \lfloor\sqrt{p}\rfloor \}\). Questo insieme contiene più di \(p\) elementi e quindi esistono due coppie diverse \((a_{1},b_{1}), (a_{2},b_{2})\), con \(0 \le a_{1},b_{1},a_{2},b_{2} \le \lfloor\sqrt{p}\rfloor \), tali che

\[ a_{1}t + b_{1} \equiv a_{2}t + b_{2} \pmod{p} \]

Se indichiamo \(x=a_{2}-a_{1}\) e \(y=b_{2}-b_{1}\) abbiamo

\[ y^{2} \equiv x^{2}t^{2} \equiv – x^{2} \pmod{p} \]

Quindi \(p|x^{2}+y^{2}\). Ma poiché \(0 < x^{2}+y^{2}<2 (\lfloor \sqrt{p}\rfloor)^{2}<2p\) allora deve essere \(p=x^{2}+y^{2}\).

Esercizio 5.1
Dimostrare che se due numeri sono somma di due quadrati, anche il loro prodotto si può esprimere come somma di due quadrati.

Soluzione
Basta ricordare la seguente formula:

\[ (a^{2}+b^{2})(c^{2}+d^{2})=(ac+bd)^{2}+(ad-bc)^{2} \]

Nel caso di un numero composto, le condizioni per poter rappresentare un intero come somma di due quadrati sono contenute nel seguente teorema di Fermat:

Teorema 5.2
Sia dato un intero positivo \(n\) con la seguente scomposizione in fattori primi:

\[ n = 2^{t}\prod_{i}p_{i}^{r_{i}} \prod_{j}q_{j}^{s_{j}} \]

dove \(p_{i} \equiv 1 \pmod{4}\) e \(q_{j} \equiv 3 \pmod{4}\). Allora è possibile scrivere \(n=x^{2}+ y^{2}\) se e solo se tutti gli esponenti \(s_{j}\) sono pari.

Per una dimostrazione vedere uno dei testi della bibliografia.

---

6) Cenni sul simbolo di Jacobi

Il simbolo di Jacobi è un’estensione del simbolo di Legendre ai numeri composti. Sia \(n\) un intero positivo con la fattorizzazione \(n=\prod_{j=1}^{k}p_{j}^{a_{j}}\). Il simbolo di Jacobi è definito come il prodotto dei simboli di Legendre relativi ai fattori primi di \(n\):

\[ \left(\frac{a}{n}\right)=\left(\frac{a}{p_{1}}\right)^{a_{1}} \dots \left(\frac{a}{p_{k}}\right)^{a_{k}} \]

Il simbolo di Jacobi \(\left(\frac{a}{1}\right)\) viene posto uguale a \(1\). Se \((a,n)>1\) allora \(\left(\frac{a}{n}\right)=0\), mentre se \((a,n)=1\) allora \(\left(\frac{a}{n}\right)=\pm 1\).
Ovviamente se \(n\) è un numero primo, il simbolo di Jacobi ha gli stessi valori del simbolo di Legendre. Notiamo che se \(\left(\frac{a}{n}\right)=-1\) allora \(a\) non è un residuo quadratico \(\pmod {n}\). Tuttavia se \(\left(\frac{a}{n}\right)=1\), con \(n\) numero composto, non si ha necessariamente che \(a\) è un residuo quadratico modulo \(n\).
Le seguenti proprietà derivano facilmente dalla definizione:

Teorema 6.1
Siano dati due interi positivi dispari \(n,m\). Allora valgono le seguenti proprietà:

\[ \begin{split} &\left(\frac{a}{n}\right)\left(\frac{a}{m}\right)=\left(\frac{a}{nm}\right) \\ &\left(\frac{a}{n}\right)\left(\frac{b}{n}\right) =\left(\frac{ab}{n}\right) \\ & a \equiv b \pmod{n} \text{ implica } \left(\frac{a}{n}\right)=\left(\frac{b}{n}\right) \\ \end{split} \]

Esempio 6.1
La congruenza \(x^{2} \equiv 2 \pmod{15}\) non ha soluzioni, come si può verificare provando con i numeri \(1,2, \cdots ,14\). Tuttavia risulta

\[ \left(\frac{2}{15}\right)=\left(\frac{2}{3}\right) \left(\frac{2}{5}\right)=(-1)(-1)=1 \]

Il simbolo di Jacobi soddisfa la stessa legge di reciprocità del simbolo di Legendre:

Teorema 6.2
Se \(n\) e \(m\) sono dispari e positivi e \((n,m)=1\), allora

\[ \left(\frac{n}{m}\right) \left(\frac{m}{n}\right) = (-1)^{\frac{n-1}{2} \frac{m-1}{2}} \]

Per la dimostrazione di questo teorema e per altre proprietà del simbolo di Jacobi vedere il testo ^[4].

Per completezza ricordiamo anche i seguenti due casi particolari:

Teorema 6.3
Se \(n\) è dispari e positivo, allora

\[ \begin{split} \left(\frac{-1}{n}\right)=(-1)^{\frac{n-1}{2}} \\ \left(\frac{2}{n}\right)=(-1)^{\frac{n^{2}-1}{8}} \\ \end{split} \]

Esercizio 6.1
Utilizzando l’esercizio 4.1) dimostrare che \(\left(\frac{15}{47}\right)=1 \), senza decomporre il numero \(15\).

Le proprietà del simbolo di Jacobi possono essere sfruttate per calcolare velocemente il simbolo di Legendre.

Esercizio 6.2
Verificare se la congruenza quadratica \(x^{2} \equiv 330 \pmod{997}\) ammette soluzioni.

Soluzione
Osserviamo che \(997\) è un numero primo. Utilizzando il simbolo di Jacobi abbiamo:

\[ \begin{split} \left(\frac{330}{997}\right) &= \left(\frac{165}{997}\right) \left(\frac{2}{997}\right)= -\left(\frac{165}{997}\right)= – \left(\frac{997}{165}\right) \\ &= -\left(\frac{7}{165}\right)= -\left(\frac{165}{7}\right)=-\left(\frac{4}{7}\right)=-1 \end{split} \]

Quindi la congruenza non ha soluzioni.

---

7) L’algoritmo di Solovay-Strassen

Definizione 7.1
Se \(n\) è un intero positivo dispari composto e \(b\) è un intero tale che \((n,b)=1\), allora \(n\) si chiama pseudoprimo di Eulero rispetto alla base \(b\) se risulta:

\[ b^{\frac{n-1}{2}} \equiv \left(\frac{b}{n} \right) \pmod {n} \]

Esercizio 7.1
Dimostrare che il numero \(1729=7 \cdot 13 \cdot 19\) non è uno pseudprimo di Eulero in base \(11\).

Soluzione

\[ \left (\frac{11}{1729} \right) = \left (\frac{1729}{11} \right) = \left (\frac{2}{11} \right) = -1 \]

D’altra parte \(11^{864} \equiv 1 \pmod{7,13,19}\) per il teorema di Fermat, e quindi \(11^{864} \equiv 1 \pmod{1729}\).

Esercizio 7.2
Dimostrare che il numero \(561=187*3\) è uno pseudoprimo di Eulero in base \(2\) e non è uno pseudoprimo di Eulero in base \(5\).

Sappiamo che se \(n\) è primo allora è anche uno pseudoprimo di Eulero. D’altra parte se n è composto si può dimostrare la relazione non vale per almeno la metà dei numeri della classe residuo \(\pmod{p}\). Infatti vale il seguente teorema:

Teorema 7.1
Se \(n\) è un composto dispari, allora non passa il test \(b^{\frac{n-1}{2}} \equiv \left(\frac{b}{n} \right) \pmod {n}\) per almeno metà delle basi \(b\) con \((b,n)=1\).

Per una dimostrazione vedi ad esempio il testo di Koblitz.
Sfruttando le proprietà precedenti possiamo implementare un algoritmo probabilistico con il Metodo Montecarlo per determinare se un dato intero è primo. L’idea dell’algoritmo è di testare più volte le basi \(b\) scelte in maniera random. Se la relazione non è soddisfatta per almeno un valore di \(b\) allora il numero \(n\) è composto. Se invece si effettua il test per \(k\) volte e la relazione risulta sempre vera, allora possiamo affermare che il numero \(n\) è primo con probabilità almeno \(\left(1- \frac{1}{2^{k}}\right)\). Lo pseudocodice per l’algoritmo di Solovay-Strassen è il seguente:

INPUT: intero n >= 3
       intero positivo k 
OUTPUT:  0 se n è composto 
         1 se n è probabilmente primo

for (i=1,...,k) {
   //Scegli in modo random nell'insieme {1,...,n-1}
   a = random(1,n-1); 
   if (gcd(a,n) != 1)
      return 0;
   if (a/n != a^((n-1)/2) mod n)
      return 0;
}
return 1;

Per un’analisi della complessità dell’algoritmo si può consultare sempre il testo di Koblitz.

---

Conclusione

La legge di reciprocità quadratica è uno dei risultati più belli e importanti della teoria dei numeri. Lo stesso Gauss e altri matematici nel periodo successivo hanno generalizzato la legge in diverse direzioni, dimostrando ad esempio le leggi di reciprocità cubica e biquadratica. Inoltre la ricerca di leggi di reciprocità sempre più generali ha contribuito allo sviluppo di altri settori importanti dell’algebra, come gli interi di Gauss e in generale dei numeri algebrici.
Per uno studio approfondito, anche dal punto di vista storico, vedere il testo ^[5].

---

Bibliografia

^[1]C. F. Gauss – Disquisitiones Arithmeticae (Springer)

^[2]Erdos, Suranyi – Topics in the Theory of Numbers (Springer)

^[3]Hardy, Wright – An Introduction to the Theory of Numbers (Oxford University Press)

^[4]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991)

^[5]F. Lemmermeyer – Reciprocity Laws: From Euler to Eisenstein (Springer)