In un precedente articolo abbiamo introdotto alcuni esempi di frattali, illustrando le loro principali caratteristiche, qualitative e quantitative: autosimilarità, irregolarità geometrica, dimensione frazionaria. Per approfondire lo studio della scienza dei frattali è necessario in primo luogo dare una definizione più rigorosa del contesto matematico in cui sono definiti gli oggetti frattali.
Ogni frattale è una forma geometrica che possiamo considerare immersa in uno spazio euclideo \(\mathbb{R}^{n}\) di dimensione \(n=1,2,3\) o anche maggiore. Per definire lo spazio matematico dei frattali è necessario richiamare alcuni concetti sulla topologia degli spazi metrici.
1) Spazi metrici
Definizione 1.1
Uno spazio metrico \((X,d)\) è una coppia formata da un insieme \(X\) e una funzione \(d: X \times X \to \mathbb{R}\), chiamata funzione distanza, che soddisfa i seguenti assiomi:
Esempio 1.1 – La metrica discreta
Dato un insieme \(X\), definiamo la seguente metrica:
Si verifica facilmente che la funzione definita, chiamata metrica discreta, soddisfa gli assiomi e quindi la coppia \((X,d)\) è uno spazio metrico.
Esempio 1.2 – La metrica Euclidea
Sia \(X=\mathbb{R^{n}}\) lo spazio euclideo ad \(n\) dimensioni . Se \(x,y\) sono due punti dello spazio, la metrica euclidea è così definita:
Esempio 1.3 – I numeri razionali e irrazionali
Abbiamo visto che l’insieme dei numeri reali \(\mathbb{R}\) è uno spazio metrico con la metrica \(d(x,y)=|x-y|\). Come è noto i numeri reali sono costituiti dai numeri razionali e dai numeri irrazionali; quindi \(\mathbb{R}= \mathbb{Q}\cup \mathbb{I}\), dove \(\mathbb{Q}\) è l’insieme dei numeri razionali e \(\mathbb{I}\) è l’insieme dei numeri irrazionali. Questi due sottoinsiemi sono anch’essi spazi metrici con la metrica euclidea.
Esempio 1.4 – La metrica Manhattan
Nel piano\(\mathbb{R^{2}}\), oltre alla metrica euclidea, possiamo definire la seguente metrica, chiamata metrica Manhattan (Taxicab Metric). Vivendo in una città dove le strade hanno una configurazione a griglia, nord-sud e est-ovest, per andare da un punto \(A\) ad un punto \(B\) con un taxi, non si può prendere la via più breve secondo la metrica euclidea, ma si possono fare soltanto tratti orizzontali e verticali. In questa situazione dati due punti \(A(x_{1},y_{1})\) e \(B(x_{2},y_{2})\) del piano, la distanza minima per andare dal punto \(A\) al punto \(B\) è data dal seguente valore:
Per dimostrare che la funzione sopra definita soddisfa gli assiomi degli spazi metrici, ricordare che dati due numeri reali qualunque \(x,y\) vale la seguente relazione: \(|x+y| \le |x| + |y|\).
2) Spazi topologici
Definizione 2.1
Uno spazio topologico è una coppia \((X,A)\) costituita da un insieme \(X\) e una famiglia di sottoinsiemi di \(X\), indicata con \(A\), chiamati gli insiemi aperti, che soddisfa i seguenti assiomi:
- A1 – l’insieme universo \(X\) e l’insieme vuoto \(\emptyset\) sono aperti
- A2 – l’unione di un numero qualunque, finito o infinito, di aperti è un aperto
- A3 – l’intersezione di un numero finito di aperti è aperto
Gli insiemi complementari degli aperti vengono chiamati gli insiemi chiusi. La definizione di spazio topologico non presuppone alcuna struttura algebrica sull’insieme \(X\). Per definire una struttura topologica bisogna quindi soltanto definire quali sottoinsiemi sono aperti.
Esempio 2.1 – La topologia banale o indiscreta
Sia \(X\) un insieme qualsiasi. La topologia banale (o indiscreta) su \(X\) è la topologia in cui \(A = \{\emptyset, X\}\), cioè gli aperti sono soltanto i sottoinsiemi banali.
Esempio 2.2 – La topologia discreta
Sia \(X\) un insieme qualsiasi. La topologia discreta definisce come aperti tutti i sottoinsiemi di \(X\). La famiglia di tutti i sottoinsiemi di \(X\) si chiama insieme delle parti di \(X\), indicato con \(P(X)\).
Esercizio 2.1
Dimostrare che se \(|X|=n\), allora il numero di aperti nella topologia discreta è \(2^{n}\).
3) Topologia negli spazi metrici
Su ogni spazio metrico \((X,d)\) può essere definita in modo naturale una topologia indotta dalla metrica.
Definizione 3.1
Dato uno spazio metrico \((X,d)\), definiamo sfera aperta (o palla aperta) di raggio \(r\) e centro \(x\), l’insieme
Definiamo ora aperti tutti i sottoinsiemi di \(X\) che sono unione di sfere aperte. Si dimostra facilmente che con questa definizione di aperti l’insieme \(X\) assume una struttura di spazio topologico.
Esempio 3.1
La topologia euclidea di \(R^{n}\) è quella indotta dalla metrica euclidea:
Definizione 3.2 – Limite di una successione
Una successione di punti \(\{x_{n}\}\) di uno spazio metrico \((X,d)\) è convergente ad un punto \(x \in X\) (o in modo equivalente ha come limite un punto \(x \in X\)) al tendere di \(n\) all’infinito, se risulta verificata le seguente condizione:
In questo caso si utilizza la seguente notazione:
\[ \lim_{n\to\infty}{x_{n}} = x \]Definizione 3.3 – Successione di Cauchy
Una successione di punti \(\{x_{n}\}\) di uno spazio metrico \((X,d)\) di dice che è una successione di Cauchy se risulta:
Esercizio 3.1
Dimostrare che ogni successione convergente è anche una successione di Cauchy.
Definizione 3.4 – Spazio metrico completo
Uno spazio metrico si dice completo se ogni successione di Cauchy \(\{x_{n}\}\) è convergente ad un punto dello spazio \(X\).
Esempio 3.2
L’intervallo aperto \(X=(0,1)\) della retta reale è uno spazio metrico, ma non è completo. Ad esempio la successione \(\{x_{n}= \frac{1}{n}\}\) è una successione di Cauchy, ma non converge ad un punto dell’intervallo.
Invece l’intervallo chiuso \([0,1]\) è uno spazio metrico completo.
Definizione 3.5 – Insieme compatto
Sia dato uno spazio metrico \((X,d)\). Un sottoinsieme \(C\) di \(X\) si dice compatto se ogni successione infinita \(\{x_{n}\}\) contiene una sottosuccessione che ha limite che appartiene ad \(C\).
Vale il seguente fondamentale teorema dell’analisi matematica:
Teorema 3.1 – Heine-Borel
Un sottoinsieme dello spazio euclideo \(R^{n}\) è compatto se e solo se è chiuso e limitato.
Per approfondire lo studio della Topologia e degli Spazi Metrici si può consultare [1] (disponibile su Amazon.com). Come tutti i testi della Collana Schaum è caratterizzato dalla presenza di numerosi esercizi svolti.
4) Lo spazio metrico dei frattali
A questo punto abbiamo tutti gli strumenti necessari per definire lo spazio metrico dei frattali.
Supponiamo di avere uno spazio metrico \((X,d)\) completo. In ogni spazio metrico abbiamo gli elementi primitivi, chiamati punti dello spazio. Inoltre nello spazio metrico abbiamo definito la classe dei sottoinsiemi compatti, i quali possono essere costituiti ognuno da un numero finito o infinito di punti.
Definizione 4.1
Dato uno spazio metrico \((X,d)\). Lo spazio dei frattali \(H(X)\) è uno spazio i cui punti sono i sottoinsiemi compatti dello spazio metrico \(X\), escludendo l’insieme vuoto. Per completare la definizione dobbiamo definire una funzione distanza che fornisca la struttura di spazio metrico.
Definizione 4.2
Sia \((X,d)\) uno spazio metrico completo. Sia \(x \in X\) e \(C\) un sottoinsieme compatto di \(X\), cioè un punto dello spazio \(H(X)\). Definiamo la distanza del punto \(x\) dall’insieme \(C\):
Dall’analisi matematica sappiamo che il minimo valore esiste in base all’ipotesi di compattezza dell’insieme non vuoto \(C\).
A questo punto possiamo definire la metrica sullo spazio dei frattali \(H(X)\):
Definizione 4.3
Sia \((X,d)\) uno spazio metrico completo. Dati due insiemi compatti \(A,B \in X\) (di fatto due punti dello spazio \(H(X)\)), definiamo la distanza fra i due punti \(A,B\) dello spazio \(H(X)\) al seguente modo:
La funzione sopra definita non soddisfa la proprietà di simmetria. Infatti in genere \(d(A,B) \ne d(B,A)\). Quindi la funzione \(d\) non rappresenta una metrica sullo spazio \(H(X)\). Per avere una metrica viene utilizzata la seguente definizione proposta dal matematico Felix Hausdorff (1868-1942).
Definizione 4.4
La distanza di Hausdorff \(h(A,B)\) fra due punti \(A,B\) dello spazio dei frattali \(H(X)\) è data dalla seguente formula:
dove max indica il valore più grande fra i due valori. Si può dimostrare che la funzione sopra definita soddisfa gli assiomi della distanza. Inoltre se lo spazio metrico \(X\) è completo, anche lo spazio metrico \(H(X)\) è completo. Per una dimostrazione vedere il libro di Barnsley.
5) Trasformazioni lineari e affini
Nel piano \(R^{2}\), fissata una origine \(O\), ad ogni punto del piano corrisponde il vettore \(\mathbf{OP}\). Con la notazione \(P+Q\) si intende il punto del piano identificato dal vettore somma di \(\mathbf{OP}\) e \(\mathbf{OQ}\). Una trasformazione lineare \(f\) nel piano è una funzione che ad ogni punto \(P(x,y)\) del piano associa un altro punto del piano \(f(P)\), tale che se \(P,Q\) sono due punti qualunque del piano e \(\lambda\) è un numero reale, siano verificate le seguenti proprietà:
\[ \begin{split} f(P+Q) &= f(P) + f(Q) \\ f (\lambda P) &= \lambda f(P) \\ \end{split} \]Nel piano \(\mathbb{R^{2}}\) una trasformazione lineare può essere rappresentata con il seguente sistema di due equazioni lineari:
\[ \begin{cases} y_{1}&= a_{11} x_1 + a_{12} x_2 \\ y_{2}&= a_{21} x_1 + a_{22} x_2 \\ \end{cases} \]Il sistema può essere scritto in forma compatta come \(y=Ax\), dove \(A\) è la matrice \(n\times n\) con coefficienti \(a_{ij}\), mentre \(x,y\) sono due vettori colonna. Ricordiamo che una matrice \(A\) si dice invertibile se esiste un’altra matrice, indicata con \(A^{-1}\) tale che \(AA^{-1}=I\), dove \(I\) è la matrice identità, i cui elementi diagonali sono tutti uguali a \(1\) e gli altri sono uguali a zero.
Definizione 5.1
Una trasformazione affine nel piano è una trasformazione della forma \(f(x) = Ax + t\), dove \(A\) è una matrice invertibile, e \(x,t\) sono vettori.
Di fatto una trasformazione affine è la composizione di una trasformazione lineare e di una traslazione. Il vettore \(t=(e,f)\) è responsabile della traslazione. Nel caso dello spazio \(X = R^{2}\) la trasformazione affine può essere scritta in questo modo:
\[ \begin{align} f(x) &= Ax + t \\ &= \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} e \\ f \end{bmatrix} \end{align} \]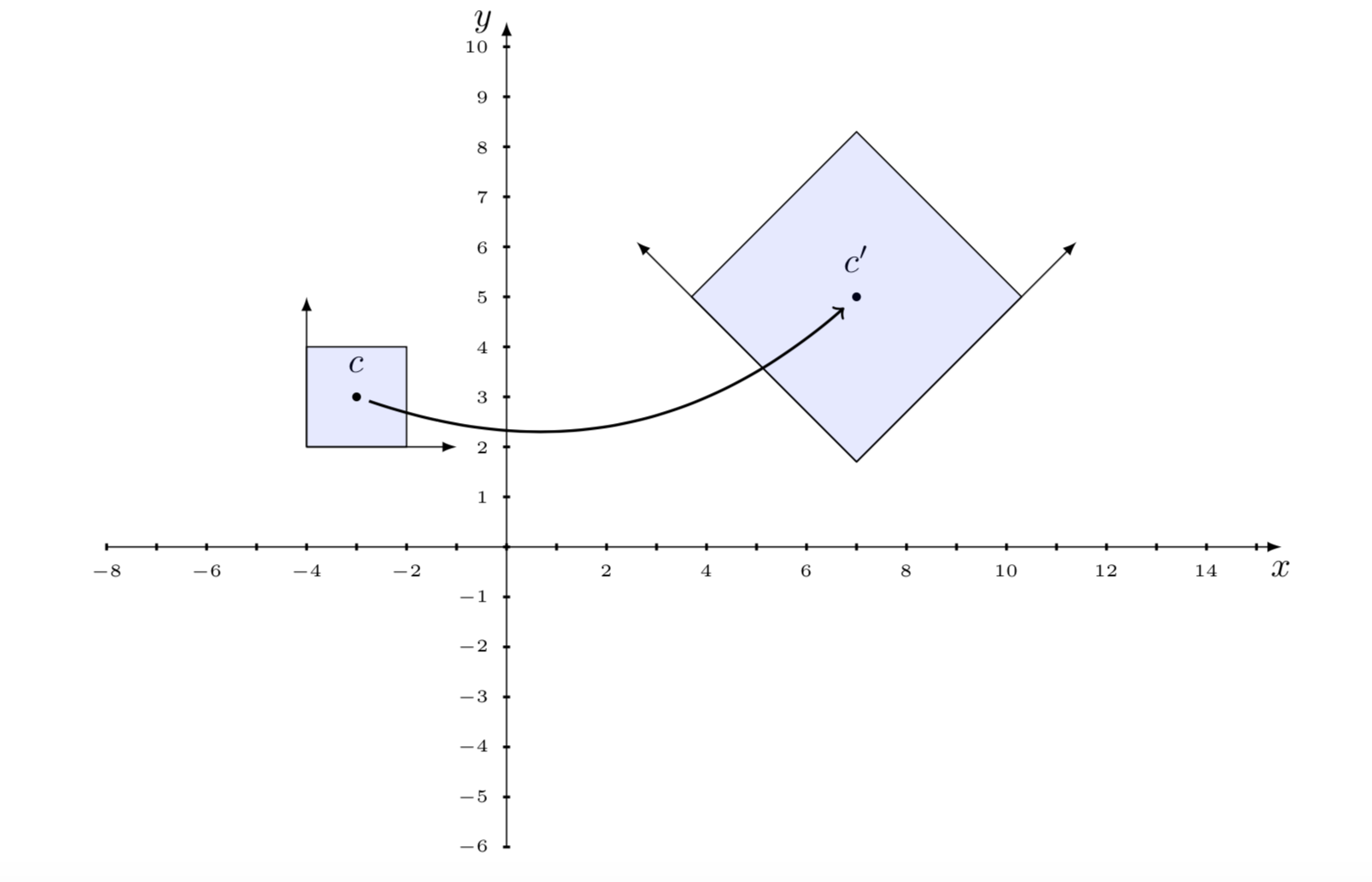
Gli oggetti frattali sono in genere sottoinsiemi dello spazio euclideo \(\mathbb{R^{n}}\), generati tramite trasformazioni affini. È di fondamentale importanza studiare le proprietà geometriche che rimangono invariate rispetto ad una trasformazione affine.
Una trasformazione affine è una composizione di rotazioni, traslazioni, dilatazioni e contrazioni. Le trasformazioni affini preservano la collinearità (cioè punti che appartengono inizialmente ad una retta, restano sulla retta) e il rapporto delle distanze (punti medi di un segmento rimangono anche dopo la trasformazione). Non conservano gli angoli e le lunghezze. La relazione di affinità è una estensione delle relazioni di congruenza e similitudine studiate nella geometria euclidea classica. Una triangolo resta sempre un triangolo dopo una trasformazione affine, anche se non necessariamente ha la stessa area (congruenza) o è simile a quello iniziale.
Per comprendere le trasformazioni affini è necessario ricordare le proprietà più importanti dell’algebra dei vettori e delle matrici. Per questo si può consultare il seguente testo, che propone molti esercizi svolti: [2]. Vedere anche gli articoli già pubblicati in questo blog sull’algebra dei vettori e delle matrici.
Esercizio 5.1
Data una trasformazione affine \(f(x)=Ax+t\) trovare la trasformazione inversa \(g(x)\) tale che \(f(g(x))=x\).
Suggerimento
Moltiplicare a destra e sinistra per la matrice inversa \(A^{-1}\).
Teorema 5.1
Una composizione di due trasformazioni affini è una trasformazione affine.
Dimostrazione
Siano \(f(x)=Ax+ t\), \(g(x)=Bx+s\) due trasformazioni affini. Allora \((g \circ f)(x)=g(f(x))=(BA)(x) + (Bt+s)\). Poiché \(A,B\) sono matrici invertibili, lo è anche la matrice prodotto \(BA\), e quindi la funzione composta \(g \circ f\) è una trasformazione affine.
5.1) Coordinate omogenee
Una trasformazione affine nel piano può esser rappresentata in modo compatto utilizzando le coordinate omogenee, cioè una matrice \(3 \times 3\). Di fatto si aggiunge una colonna con i parametri relativi alla traslazione e una riga con i valori \((0,0,1)\) (Per le trasformazioni nello spazio \(R^{3}\) si utilizzerà un matrice \(4 \times 4\)):
\[ Ax + t= \begin{bmatrix} a & b & e\\ c & d & f\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]Le matrici per le trasformazioni di base sono le seguenti:
Traslazione \((d_{x},d_{y})\):
\[ \begin{bmatrix} 1 & 0 & d_{x} \\ 0 & 1 & d_{y}\\ 0 & 0 & 1 \end{bmatrix} \]Rotazione di un angolo \(\theta\):
\[ \begin{bmatrix} \cos \theta & – \sin \theta & 0 \\ \sin \theta & \cos \theta & 0\\ 0 & 0 & 1 \end{bmatrix} \]Cambiamento di scala \((s_{x},s_{y})\):
\[ \begin{bmatrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0\\ 0 & 0 & 1 \end{bmatrix} \]Deformazione (shear):
\[ \begin{bmatrix} 1 & a_{x} & 0 \\ b_{y} & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]Esempio 5.1
La seguente matrice rappresenta una traslazione di una unità nella direzione dell’asse \(x\) e di due unità nella direzione dell’asse \(y\). Non vengono cambiate le dimensioni e non c’è rotazione.
Esercizio 5.2
Determinare l’effetto della trasformazione nel piano mediante la seguente matrice [\(\cos(30^\circ)= \sqrt \frac{3}{2}\) , \(\sin (30^\circ)= \frac{1}{2}\) ]:
6) Trasformazioni negli spazi metrici
Definizione 6.1
Dato uno spazio metrico \((X,d)\) e una funzione \(f: X \to X\). Si dice che la funzione è una contrazione dello spazio metrico se esiste un numero reale \(0 \le c <1\) tale che risulti:
Definizione 6.2
Data una funzione \(f: X \to X\). Un punto \(x_{0} \in X\) si dice punto fisso per la funzione se risulta \(f(x_{0})=x_{0}\).
Esercizio 6.1
Consideriamo lo spazio metrico \((R^{2},d)\), dove \(d\) è la metrica euclidea. Sia data la trasformazione \(f: \mathbb{R^{2}} \to \mathbb{R^{2}}\) così definita:
Dimostrare sotto quali condizioni dei coefficienti \(a,b,c\) è una contrazione e in tal caso trovare il punto fisso.
Risposta: [\( a,c >1; x=\frac{ab}{a-1},y=\frac{bc}{c-1}\)]
Per le contrazioni vale il seguente fondamentale teorema di Banach (1892-1945) e Caccioppoli (1904-1959):
Teorema 6.1 – Banach-Caccioppoli
Sia \((X,d)\) uno spazio metrico completo e \(f: X \to X\) una funzione di contrazione dello spazio. Allora la funzione \(f\) ha un unico punto fisso in \(X\). Inoltre preso un punto qualunque \(x \in X\), la successione \(\{x,f(x),f(f(x)), \cdots \}\) converge al punto fisso di \(f\).
Per la dimostrazione vedere un testo di analisi matematica; ad esempio [3].
Esempio 6.1
Un’applicazione di questo teorema è la ricerca di una soluzione dell’equazione \(f(x)=0\). In primo luogo si scrive l’equazione nella forma \(x=T(x)\), e quindi si definisce uno schema di iterazione \(x_{n+1}=T(x_{n})\), partendo da un valore iniziale \(x_{0}\). Sotto opportune condizioni la successione tende ad un punto fisso di \(T(x)\), cioè ad uno zero della funzione \(f(x)\).
Un esempio importante è l’algoritmo di Newton per trovare le radici di una funzione. Supponiamo di voler trovare le soluzioni della funzione \(x^{2}- a=0\). Si scrive l’equazione nella forma \(x=\frac{1}{2}(x + \frac{a}{x})\), e si imposta lo schema iterativo: \(x_{n+1}= \frac{1}{2}(x_{n} + \frac{a}{x_{n}})\). Si può dimostrare che scegliendo opportunamente il punto iniziale \(x_{0}\) la successione converge al valore \(\sqrt{a}\), che è il punto fisso e anche la radice dell’equazione iniziale.
7) Sistema di funzioni iterate
Come abbiamo visto in precedenza una trasformazione affine nello spazio euclideo \(R^{2}\) che trasforma un punto \((x_{n},y_{n})\) nel punto \((x_{n+1},y_{n+1})\), può essere descritta con le seguenti equazioni:
\[ \begin{split} x_{n+1} = a x_{n} + by_{n}+ e \\ y_{n+1} = c x_{n} + dy_{n}+ f \\ \end{split} \]I parametri \(a,b,c,d\) producono una rotazione e un cambiamento di scala in funzione della loro grandezza; i parametri \(e,f\) realizzano una traslazione del punto. Se prendiamo alcuni punti della frontiera di un qualunque oggetto, e applichiamo ad ognuno dei punti queste funzioni, possiamo ottenere una trasformazione dell’intera figura, fatta di rotazioni, traslazioni e cambiamenti di scala. La nuova figura avrà in genere la proprietà della auto-similarità con la figura originale, una delle proprietà caratteristiche dei frattali.
Uno dei modi più comuni per generare le immagini frattali è quello di utilizzare un insieme attrattore di un sistema di funzioni iterate (IFS) . Ogni IFS è costituito da trasformazioni affini con rotazioni, traslazioni e cambiamenti di scala. Normalmente vengono utilizzati due tipi di algoritmi, uno deterministico e un altro probabilistico.
Per uno studio approfondito degli IFS vedere il testo fondamentale di Barnsley[4].
7.1) Sistema di funzioni iterate deterministico
Definizione 7.1
Un sistema di funzioni iterate (IFS) deterministico è una collezione di trasformazioni affini \(\{T_{1}, \dots T_{n}\}\):
Il seguente teorema (vedi Barnsley) è fondamentale:
Teorema 7.1
Sia dato un Sistema di Funzioni Iterate \(\{H(X); T_{1},T_{2}, \cdots ,T_{n} \}\), con fattore di contrazione \(c\). Per ogni insieme \(A \in H(X)\) definiamo l’insieme unione \(W(A) = \cup (T_{i}(A)\). Allora:
– \(W(A)\) è una funzione di contrazione con fattore \(c\)
– esiste un unico punto fisso \(K \in H(X)\) tale che \(K=W(K)= \cup T_{i}(K)\)
Il punto fisso \(K\) viene ottenuto come limite all’infinito del processo di iterazione applicato all’insieme \(A\).
Procedura per creare un frattale con il metodo IFS deterministico
L’algoritmo deterministico prende un insieme di punti \(A\), ad esempio i punti di una figura geometrica, al quale applica le \(n\) trasformazioni affini, ottenendo così un nuovo insieme costituito dalla unione di \(n\) insiemi di punti:
\[ W(A)= T_{1}(A) \cup T_{2}(A) \cup \cdots \cup T_{n}(A) \]L’operatore \(W\) viene chiamato operatore di Hutchinson.
Ad esempio se l’insieme iniziale \(A\) è costituito da un punto soltanto, dopo la prima iterazione l’insieme \(W(A)\) contiene \(n\) punti. Si continua il processo di iterazione partendo dall’insieme \(W(A)\) fino a che l’unione di tutti gli insiemi ottenuti nell’ultima iterazione si avvicina alla figura che costituisce l’attrattore del sistema IFS. Ogni IFS ha associato un attrattore frattale, che in genere è indipendente dalla scelta iniziale dei punti.
7.2) Sistema di funzioni iterate random
Come abbiamo accennato in precedenza, esiste anche una versione non deterministica dell’algoritmo IFS. Si definisce una distribuzione di probabilità per le varie trasformazioni, e ad ogni iterazione, invece di applicare tutte le trasformazioni, si sceglie una trasformazione in base alla sua probabilità.
Definizione 7.2
Un sistema di funzioni iterate (IFS) di tipo non deterministico è una collezione di trasformazioni affini \(\{T_{1}, \dots T_{n}\}\), associate con una distribuzione di probabilità \(\{P_{1}, \cdots P_{n} \}\):
Invece di applicare le funzioni ad un insieme di punti, l’esecuzione di un sistema iterate random inizia scegliendo un punto iniziale del piano. Quindi si sceglie una delle \(n\) trasformazioni del sistema in modo casuale, in base alle singole probabilità di ogni iterazione. Questo processo viene ripetuto teoricamente all’infinito. Naturalmente nella pratica quando si genera l’immagine grafica ci si ferma dopo un numero finito di iterazioni. Dopo un certo numero di iterazioni, l’insieme dei punti generati diventa arbitrariamente vicino all’insieme attrattore del sistema IFS.
8) Il triangolo di Sierpinski
Il Triangolo di Sierpinski (Sierpinski Gasket) è una figura geometrica proposta dal matematico polacco W. Sierpinski (1882-1969), che richiede i seguenti passi per la sua costruzione:
- si inizia con un triangolo equilatero, indicato con \(A_{0}\), e si individuano i punti medi dei tre lati
- si connettono i tre punti medi fra loro e si elimina il triangolo che viene creato, non includendo la sua frontiera; la figura rimasta viene indicata con \(A_{1}\)
- su ognuno dei tre triangoli che sono rimasti si ripete la procedura, ottenendo \(A_{2}\), e così via all’infinito

Il processo iterativo crea una successione infinita di insiemi:
\[ A_{0} \supset A_{1} \supset A_{2} \supset \cdots A_{N} \cdots \]Il triangolo di Sierpinski è l’insieme dei punti che rimangono dopo che la procedura viene ripetuta all’infinito.
Di fatto l’immagine iniziale viene sottoposta ad un insieme di trasformazioni affini; si tratta quindi di un sistema di funzioni iterate. In ogni fase, da ogni triangolo blu vengono creati tre triangoli blu e un triangolo bianco. Ognuno dei nuovi triangoli ha il perimetro uguale alle metà del triangolo padre e l’area uguale ad un quarto di quella del triangolo padre. La successione degli insiemi \(\{A _{0},A_{1},A_{2}, \cdots \}\) è una successione di insiemi compatti, in quanto in ogni passo eliminiamo il triangolo aperto al centro. Dopo un numero infinito di iterazioni l’immagine converge all’attrattore. Il sistema di equazioni che definiscono il triangolo di Sierpinski è il seguente:
Si può anche cambiare la procedura, creando un triangolo rettangolo con tre vertici \(\{(0,0),(1,0),(0,1)\}\):
\[ \begin{split} \\ T_{1}(x,y)&= \left(\frac{x}{2}, \frac{y}{2}\right) \\ T_{2}(x,y)&= \left(\frac{x}{2} + \frac{1}{2},\frac{y}{2}\right) \\ T_{3}(x,y)&= \left(\frac{x}{2},\frac{y}{2} + \frac{1}{2}\right) \end{split} \]Le funzioni \(\{T_{1},T_{2},T_{3} \}\) sono trasformazioni affini, traslazioni e cambiamenti di scala. Chiamiamo \(A_{0}\) l’immagine iniziale del triangolo con i vertici \((0,0),(1,0),(0,1)\). Dopo la prima iterazione otteniamo l’immagine
\[ A_{1}= T(A_{0})=T_{1}(A_{0}) \cup T_{2}(A_{0}) \cup T_{3}(A_{0}) \]dove la trasformazione \(T\) è l’unione delle tre trasformazioni elementari. Proseguendo abbiamo \(A_{2}=T(A_{1})=T^{2}(A_{0})\), ecc. Il triangolo di Sierpinski è il limite di questa successione di insiemi compatti:
\[ \text {Triangolo Sierpinski} = \lim_{n\to\infty} T^{n}(A_{0}) \]8.1) Area e perimetro del triangolo di Sierpinski
Per calcolare l’area e il perimetro del triangolo di Sierpinski utilizziamo la seguente tabella:
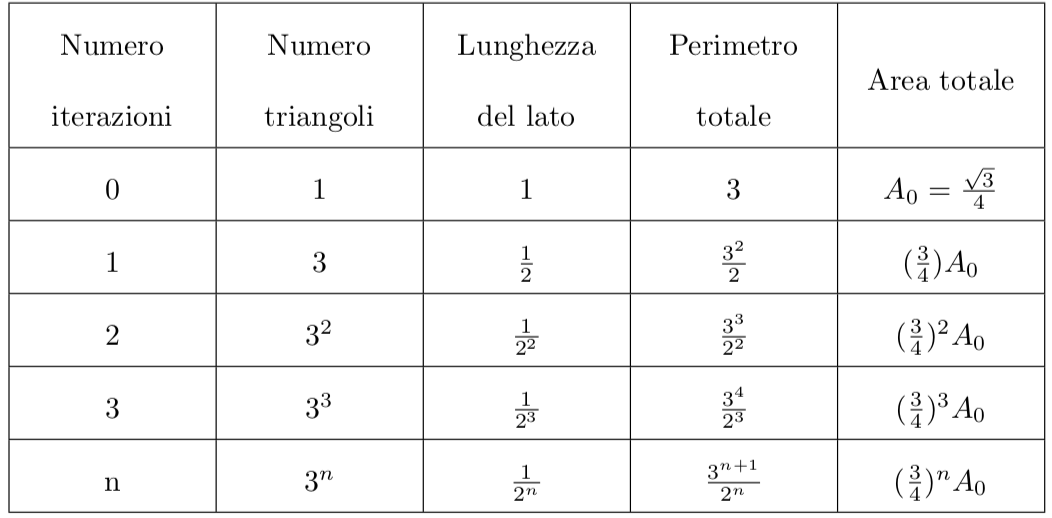
Dalla tabella possiamo concludere che i valori cercati del perimetro e dell’area del triangolo di Sierpinski sono i seguenti:
\[ \begin{split} \text {Perimetro} &= \lim_{n\to\infty} \left(\frac{3^{n+1}}{2^{n}}\right)= \infty \\ \text {Area} &= \lim_{n\to\infty} \left(\frac{3}{4}\right)^{n} \cdot A_{0}=0 \\ \end{split} \]8.2) Dimensione del triangolo di Sierpinski
Nel caso del triangolo di Sierpinski ad ogni iterazione abbiamo \(N= 3^{n}\) triangoli, mentre la lunghezza dei lati dei triangoli è \(L= \frac{1}{2^{n}}\). Quindi per la dimensione troviamo il seguente valore:
\[ d = \lim_{n\to\infty} \frac{\ln 3^{n}}{\ln 2^{n}} = \frac{\ln 3}{\ln 2} \approx 1,58496 \]La dimensione può essere calcolata anche secondo un altro procedimento. Poiché il triangolo di Sierpinski è auto-similare con tre copie disgiunte di se stesso, ognuno scalato del fattore \(r=\frac{1}{2}\), la dimensione \(d\) dell’attrattore può essere calcolata risolvendo questa equazione:
\[ r^{d} + r^{d} + r^{d}= 3 \left(\frac{1}{2}\right)^{d}=1 \]Per una dimostrazione vedere il libro di Barnsley (teorema 2.3).
Conclusione
Come abbiamo visto nel presente articolo la scienza dei frattali poggia su basi solide, costituite da settori consolidati della matematica, come l’analisi, la topologia, la geometria, ecc. I frattali generati tramite computer sono oggetti molto belli e interessanti, che attraggono molte persone. Tuttavia questo è solo un aspetto; in realtà la scienza dei frattali è anche uno strumento molto importante per descrivere sistemi e processi complessi, sia naturali sia artificiali.
Bibliografia
[1]S. Lipschutz – General Topology (McGraw-Hill)
[2]S. Lipschutz – Schaum’s Outline of Linear Algebra (McGraw Hill)
[3]A. Kolmogorov, S. Fomin – Elementi di teoria delle funzioni e di analisi funzionale (Editori Riuniti)
[4]M. Barnsley – Fractals Everywhere (Academic Press)

0 commenti