Algebra dei Vettori e Videogiochi

La programmazione dei videogiochi richiede un utilizzo estensivo della matematica e della fisica. Alcune situazioni tipiche sono le seguenti: gestire il moto di oggetti nello spazio, disegnare forme geometriche sulla scena, calcolare gli effetti dopo una collisione di oggetti applicando le leggi della meccanica classica di Newton, ecc.
Un ruolo particolare riveste la geometria. Le varie forme geometriche classiche: cerchi, quadrati, poligoni, cubi, sfere, ecc. vengono utilizzate frequentemente. Le descrizione della scena è semplicemente un insieme di triangoli e colori. Anche gli oggetti più complicati come superfici curve, NURBS e altri, in realtà sono ricondotti alla compilazione di triangoli. Le forme geometriche di base possono essere manipolate sulla scena attraverso operazioni di traslazione, rotazione e cambiamento di scala, ottenendo una infinita varietà di configurazioni geometriche e spaziali.
Il calcolo vettoriale è uno dei rami della matematica utilizzati con maggiore frequenza, in particolare per simulare il movimento di corpi rigidi nello spazio, secondo le leggi della meccanica.

---

1) Definizione di vettore

Un \(\textbf{vettore}\) nel piano (2D) o nello spazio (3D) è un segmento orientato che unisce un punto \(P\) (chiamato origine o punto iniziale) con un punto \(Q\) (chiamato punto terminale).
Un vettore viene rappresentato con una linea con direzione \(\overrightarrow{PQ}\).
Un vettore ha 3 proprietà fondamentali:

• grandezza (o intensità), rappresentata dalla lunghezza del segmento, rispetto ad una prefissata unità di misura
• direzione, che coincide con la retta (geometrica) su cui giace il segmento \(\overrightarrow{PQ}\)
• verso, che coincide con l’orientazione del segmento che definisce il vettore \(\overrightarrow{PQ}\)

Si può definire anche il vettore nullo, che si riduce ad un punto e viene rappresentato con il simbolo \(\textbf{0}\).
Introducendo un sistema di riferimento cartesiano, un vettore può essere rappresentato mediante le coordinate del suo punto terminale, supponendo che il punto iniziale sia nell’origine del sistema di riferimento.

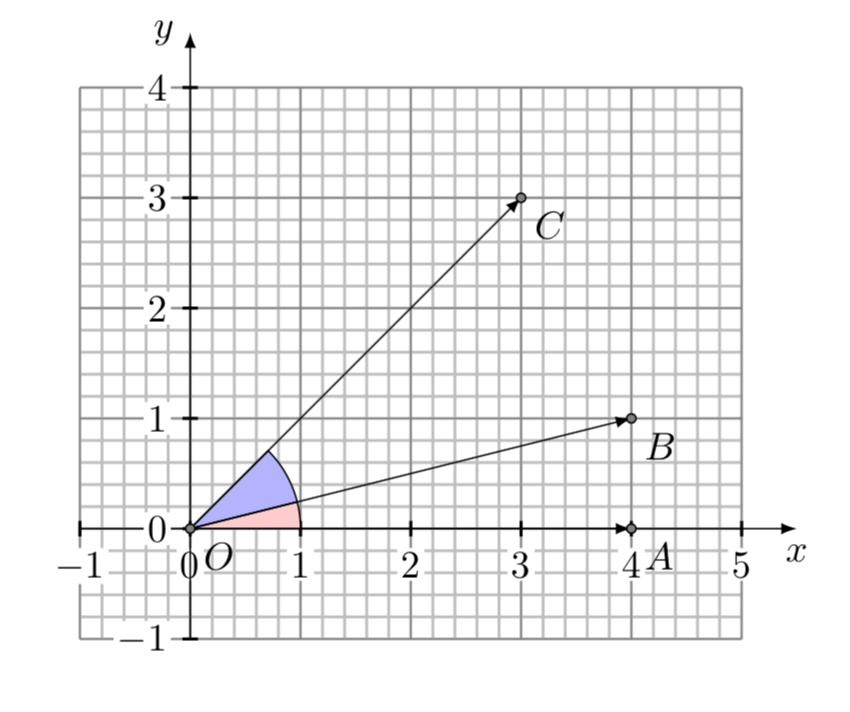
Due vettori coincidono se hanno stessa intensità e direzione; per verificare se due vettori sono uguali basta traslare uno dei due in modo da far coincidere i punti iniziali e controllare se anche i punti finali dei due vettori coincidono.
I vettori sono utilizzati in fisica per rappresentare la posizione di un corpo nel piano o nello spazio, la velocità, l’accelerazione, la forza applicata, ecc.
La grandezza di un vettore \(\overrightarrow{PQ}\), indicata con il simbolo \({\left\| {PQ}\right\|}\) può essere calcolata mediante il Teorema di Pitagora:

\[ \left\|{PQ}\right\|=\sqrt{(x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} +(z_{2}-z_{1})^{2}} \]

Un vettore normalizzato è un vettore la cui norma vale 1. Dato un vettore v, basta dividere per la sua norma, ottenendo un vettore w normalizzato:

\[ \mathbf{w} = \dfrac {\mathbf{v}} {\left\| {\mathbf{v}}\right\|} \]

---

2) Algebra dei vettori

2.1) Somma e differenza di vettori

La somma di due vettori può essere ottenuta applicato la regola del parallelogramma della geometria euclidea. Si fa coincidere il punto finale del vettore \(\mathbf{u}\) con il punto iniziale del vettore \(\mathbf{v}\). Il vettore somma \(\mathbf{u}+ \mathbf{v}\) ha come origine il punto iniziale di \(\mathbf{u}\) e come termine il punto finale di \(\mathbf{v}\). Praticamente il vettore somma coincide con la diagonale del parallelogramma generato daidue vettori. La somma dei due vettori \(\overrightarrow{OA}\) e \(\overrightarrow{OB}\) è rappresentata dal vettore \(\overrightarrow{OC}\) :

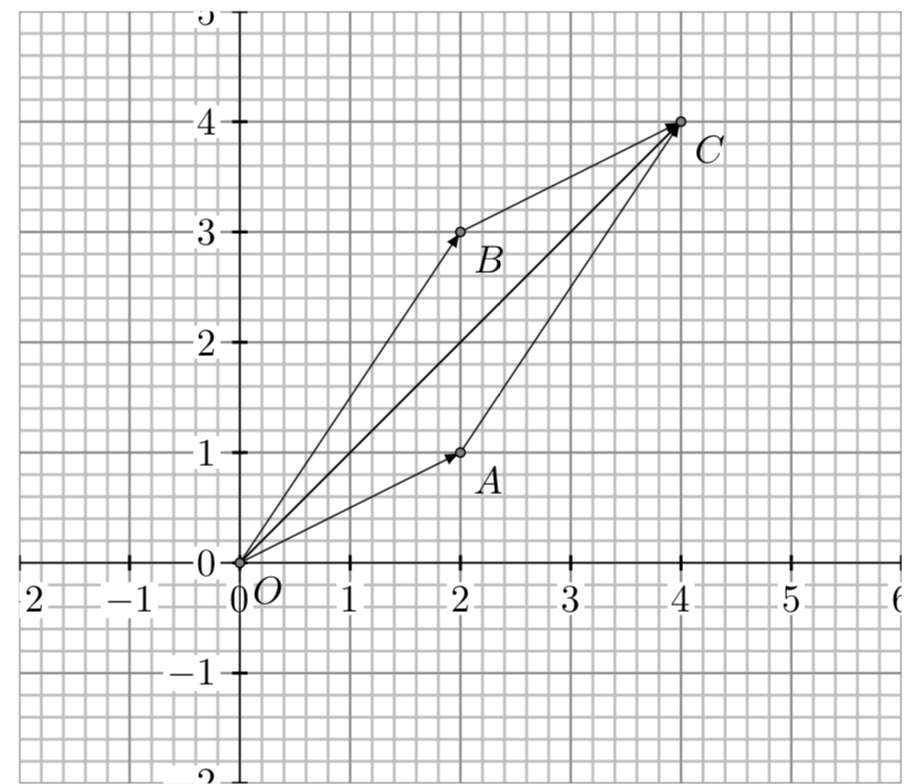
Un altro modo di calcolare il vettore somma è quello di effettuare la somma algebrica delle rispettive coordinate cartesiane dei due vettori. Per effettuare la sottrazione di due vettori, basta prima invertire il secondo vettore(cambiando il segno delle coordinate) e quindi fare la somma con il primo.

2.2) Moltiplicazione di un vettore per un numero reale (scalare)

La moltiplicazione di un vettore per uno scalare consiste nel moltiplicare ognuna delle componenti per lo scalare. In termini geometrici equivale ad una dilatazione o una contrazione del vettore.

2.3) Prodotto scalare di due vettori

Dati due vettori \(\mathbf{u}\) e \(\mathbf{v}\) nello spazio 2D, una definizione del prodotto scare è la seguente:

\[ \mathbf{u} \bullet \mathbf{v}= u_{1}v_{1} + u_{2} v_{2} \]

Si può dimostrare che una definizione equivalente di prodotto scalare è la seguente:

\[ \mathbf{u} \bullet \mathbf{v}=\left\| {\mathbf{u}} \right\| \left\| {\mathbf{v}} \right\| cos(\alpha) \]

dove \(\alpha\) è l’angolo fra i due vettori.
Mettendo insieme le due definizioni, si ottiene a seguente formula:

\[ cos(\alpha ) = \dfrac {\mathbf{u} \bullet \mathbf{v}} {\left\| {\mathbf{u}} \right\| \left\| {\mathbf{v}} \right\|} \]

Questa formula permette di determinare l’angolo fra i due vettori, calcolando il prodotto scalare a partire dalle componenti dei due vettori.

2.4) Prodotto vettoriale di due vettori

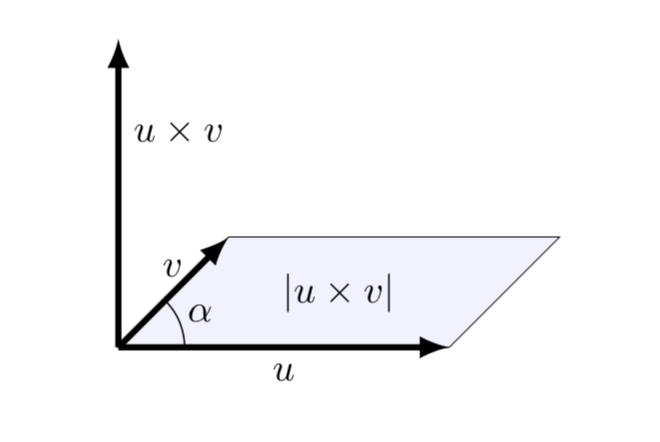
Il prodotto vettoriale di due vettori u,v è un nuovo vettore \(\mathbf{w}\) così definito:
\( \mathbf{w}= \mathbf{u} \times \mathbf{v} = |\mathbf{u}| |\mathbf{v}|\mathbf{\hat{n}} \sin \alpha \)
dove \(\alpha\) è l’angolo fra i due vettori e \(\mathbf{\hat{n}}\) è il vettore unitario (versore) perpendicolare al piano individuato dai due vettori u,v. La direzione del vettore prodotto è determinata con la regola della mano destra. Il modulo del prodotto vettoriale è uguale all’area del parallelogramma generato dai due vettori.

---

3) I vettori in Unity e il componente Transform

Unity utilizza le strutture Vector3 e Vector2 per rappresentare le informazioni sui vettori in ambiente 3D o 2D. La struttura Vector3 è quella maggiormente utilizzata. La struttura Vector2 viene usata nei giochi 2D e in altre situazioni particolari, ad esempio per memorizzare le coordinate della texture di una Mesh.
La struttura Vector3 mette a disposizione varie proprietà e metodi per effettuare le normali operazioni di calcolo vettoriale; tra queste ricordiamo le seguenti (vedi guida Vector3):

• Vector3.normalized – fornisce un nuovo vettore con norma unitaria
• Vector3.Dot – prodotto scalare di due vettori
• Vector3.Cross – prodotto vettoriale
• Vector3.MoveTowards – muove un punto di un certo tratto verso un oggetto target
• Vector3.RotateTowards – ruota un vettore di un certo angolo verso un target

Ogni oggetto (GameObject) in Unity ha una componente Transform, che gestisce le informazioni relative alla posizione, alla rotazione, e al fattore di scala.

Più precisamente tiene traccia delle seguenti informazioni:

• coordinate di posizione dell’oggetto, gestite con la struttura Vector3
• rotazione rispetto agli assi coordinati, gestita internamente con i quaternioni di Hamilton (struttura Quaternion), ma espressa nell’Inspector con gli angoli di Eulero che sono più semplici da interpretare
• il fattore di scala nelle tre direzioni gestito con la struttura Vector3

Per uno studio approfondito dell’ambiente di sviluppo Unity vedere i tutorial Unity.

---

4) Esempi di applicazione dei vettori in Unity

Esempio 1 – Spostamento di un oggetto

Ci sono diversi modi per muovere un oggetto sulla scena. In Unity la posizione di un oggetto è registrata tramite il componente Transform. Il modo più semplice per spostare un oggetto in una data posizione dello spazio è il seguente:

transform.position = new Vector3(10f, 4f, 12f); 

Questa istruzione muove istantaneamente l’oggetto nella posizione.
Per muovere un oggetto lungo una direzione, con un cambiamento continuo di coordinate, si può utilizzare anche il metodo translate:

transform.Translate(new Vector3(2f, 0f, 0f));

I parametri che vengono passati in questa funzione corrispondono alla variazione di coordinate sui 3 assi. La funzione transform.Translate non utilizza il motore fisico e quindi non gestisce le collisioni. Per ottenere un movimento in presenza di ostacoli, muri e collisioni è necessario utilizzare il componente Collider e il Rigidbody, che permettono di simulare il comportamento secondo le leggi della fisica.
Per spostare un oggetto nella direzione di un altro oggetto, bisogna effettuare una rotazione:

public Transform target; 
Vector3 posizione Relativa = target.position - transform.position; 
transform.rotation = Quaternion.LookRotation(posizioneRelativa);

Esempio 2 – Calcolare la posizione di un oggetto che si muove a velocità costante

Come è noto la scena di ogni gioco viene visualizzata tramite una successione di frame discrete, una dietro l’altra, ad una frequenza opportuna (es. 30 frame per secondo (fps)). Lo stato dei vari oggetti della scena viene continuamente aggiornato mediante il Game Loop.
La preparazione di ogni frame prevede l’esecuzione della funzione Update presente negli scripts attaccati ai vari oggetti. Se le coordinate di posizione di un oggetto vengono cambiate, si avrà l’illusione del movimento dell’oggetto stesso. Il parametro Time.DeltaTime contiene l’informazione sul tempo intercorso fra una frame e l’altra, e permette di sincronizzare le funzioni di update con il tempo fisico reale.

// posizione precedente 
position = (0, 5, 10) 

//velocità espressa in unità (es. centimetri) al secondo
velocita = (2, 3, 0) 

// aggiornamento della  posizione ad ogni nuova frame
position += velocita*Time.deltaTime 
// Se il sistema viene eseguito con 30 fps, allora il deltaTime ha
// il valore 1/30 di secondo, cioè il tempo intercorso a partire dalla precedente frame

Esempio 3 – Determinare l’angolo di rotazione per inseguire un altro oggetto

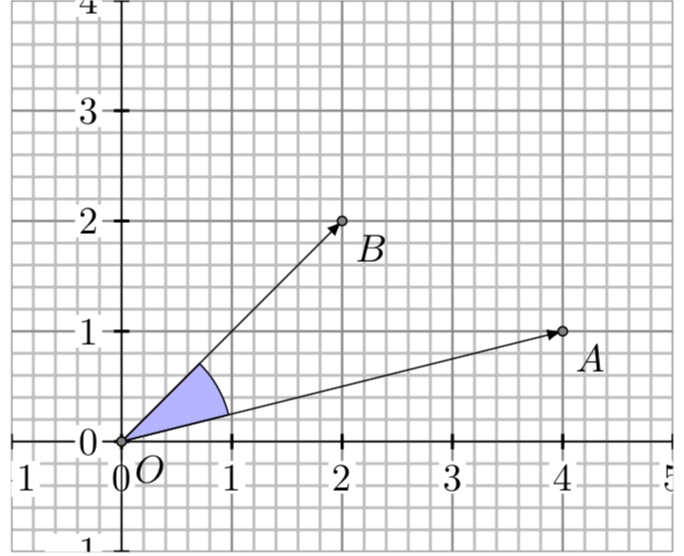
Una situazione tipica nei giochi 2D è la seguente: supponiamo che un carattere (A) debba inseguire un nemico che si trova in una situazione fissata (B). Se il carattere ad un certo momento si sta muovendo nella direzione \(\overrightarrow{OA}\), allora per arrivare al punto B è necessaria calcolare l’angolo fra i due vettori \(\mathbf{u}= \overrightarrow{OA}\) e \(\mathbf{v}=\overrightarrow{OB}\). La formula del prodotto scalare permette di trovare il coseno dell’angolo:

\[ cos(\alpha) = \dfrac {\mathbf{u} \bullet \mathbf{v}} {\left\| {\mathbf{u}} \right\| \left\| {\mathbf{v}} \right\|} \]

Quindi abbiamo:

\[ \alpha= \arccos (\dfrac {\mathbf{u} \bullet \mathbf{v}} {\left\| {\mathbf{u}} \right\| \left\| {\mathbf{v}} \right\|}) \]

dove \(\arccos() \) è la funzione inversa della funzione coseno.

Esempio 4 – Controllare se un oggetto sta davanti o dietro un altro

– Globale (World space) – unico sistema valido per tutti gli oggetti, con l’origine fissa nel centro della scena
– Locale (Local space) – uno per ogni oggetto della scena, con l’origine fissata nell’oggetto
Per passare da un sistema all’altro Unity fornisce i seguenti metodi (vedi Transform):

• TransformDirection
• TransformPoint
• TransformVector
• InverseTransformDirection
• InverseTransformPoint
• InverseTransformVector

Le prime tre trasformano le coordinate locali in globali, le successive fanno il viceversa. Per risolvere l’esempio con il prodotto scalare, è necessario trasformare le coordinati locali costanti del vettore Vector3.forward nelle corrispondenti globali.

using UnityEngine;
using System.Collections;
public class ExampleClass : MonoBehaviour {
    public Transform altroOggetto;
    void Update() {
        if (altroOggetto) {
            Vector3 forward =
       transform.TransformDirection(Vector3.forward);
       Vector3 versoAltroOggetto = altroOggetto.position - 
                transform.position;
       if (Vector3.Dot(forward, versoAltroOggetto) < 
                  & 0)
           print("L'altro oggetto si trova dietro");
       }
    }
}

In modo simile si può controllare se un oggetto sta sopra o sotto di se.

Esempio 5 – Moto circolare

Per gestire il moto circolare di un oggetto intorno ad un altro oggetto (ad esempio della Terra intorno al Sole), si possono utilizzare le seguenti istruzioni:

using UnityEngine;
using System.Collections;
public class MotoCircolare : MonoBehaviour  {
      public Transform centro;
      public float gradiAlSecondo = 30.0f;
      float x;
      float y;
   
 private void Start()
   {
    raggioVettore = transform.position - centro.position;
   }
 
 private void Update()
 {
  // calcola nuova posizione del raggioVettore
   raggioVettore = Quaternion.AngleAxis (gradiAlSecondo * Time.deltaTime,Vector3.forward) * raggioVettore;

  // aggiorna la posizione della Terra
   transform.position = center.position + raggioVettore;
  }
}

Esempio 6 – Inseguimento obiettivo (steering algorithm)

Nei giochi in cui si deve inseguire un obiettivo (target), il player ha a disposizione un dispositivo di regolazione (steer) che aggiusta la sua velocità ad ogni frame, in modo da raggiungere la posizione dell’obiettivo, utilizzando il cammino più breve possibile. La forza di correzione applicata permette al carattere di cambiare in modo continuo la sua vecchia direzione e puntare alla direzione dell’obiettivo. Graficamente la situazione può essere così rappresentata:

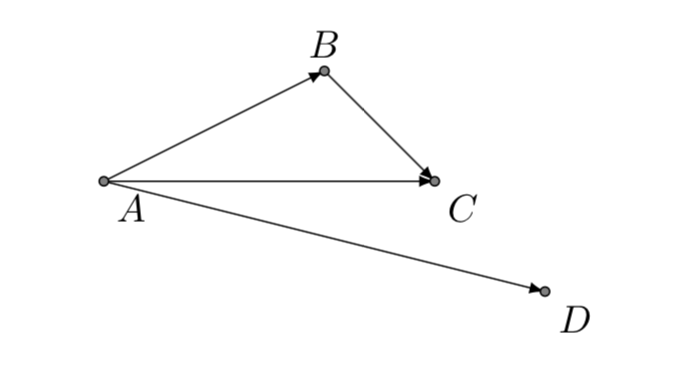
dove il punto (D) rappresenta l’obiettivo da inseguire(target) e:

• \(\overrightarrow{AB}\) : velocità corrente;
• \(\overrightarrow{AD}\) : velocità desiderata;
• \(\overrightarrow{BC}\) : forza correttiva;
• \(\overrightarrow{AC}\) : nuovo vettore velocità;

In ogni frame la forza correttiva calcolata viene sommata alla velocità del carattere che insegue, permettendo un aggiustamento continuo della traiettoria verso l’obiettivo.
L’intensità della forza viene divisa per la massa, in modo che risultino movimenti diversi a seconda della massa del carattere.
Uno schema molto semplificato per aggiustare la direzione della velocità, a partire dalla posizione attuale di una dato obiettivo (target), è il seguente:

using UnityEngine;
using System.Collections;
public class Inseguimento: MonoBehaviour  {
private float velocita = 10.0f;
private float massa = 4.0f;
private float velocitaCorrente;
private Vector3 posizioneTarget;
private Vector3 direzione;
private Vector3 velocitaDesiderata;  

private void Start()  {
    direzione = transform.forward;
}

private void Update()  {
    // normalizza velocità in funzione del framerate
     velocitaCorrente =  velocita * Time.deltaTime;
    // calcola nuova direzione
     direzione += CorreggiDirezione(posizioneTarget);
    // aggiorna posizione e orientamento inseguitore
     transform.position += direzione;   
     transform.rotation = Quaternion.LookRotation(direction); 
}

public Vector3 CorreggiDirezione(Vector3 posizioneTarget)  {
   // calcolo  del vettore velocità desiderato
     velocitaDesiderata = (posizioneTarget - transform.position);
     velocitaDesiderata.Normalize();   
     velocitaDesiderata*= velocitaCorrente;

   // calcolo della forza e dell'accelerazione		
     Vector3 forzaSterzo = velocitaDesiderata - direzione; 
     Vector3 accelerazione = forzaSterzo / massa;
     return accelerazione;
    }
}

Naturalmente una implementazione reale dell’algoritmo deve gestire molte situazioni, come il movimento variabile del target, la presenza di ostacoli, la possibilità di collisioni con altri oggetti, il comportamento da seguire quando la distanza con il target è al di sotto di una data soglia, ecc.

---

Conclusione

La matematica è lo strumento fondamentale per lo sviluppo dei videogiochi, sia quelli elementari sia soprattutto quelli più complessi. Oltre al calcolo vettoriale molti altri settori della matematica hanno un ruolo indispensabile (geometria, trigonometria, equazioni differenziali, calcolo delle probabilità, ecc.).
Nei giochi più interessanti i caratteri sono immersi in un mondo che cerca di simulare l’ambiente reale. Per rendere realistico il comportamento dei protagonisti del gioco è necessario simulare le leggi della fisica, e quindi risolvere le complesse equazioni matematiche che ne stanno alla base. Il calcolo della traiettoria di un aereo, la guida di una automobile ad alta velocità, la discesa lungo una pista di neve, il salto di un ostacolo, non sarebbero possibili senza l’ausilio degli strumenti matematici.