La geometria dei numeri è una branca della Teoria dei numeri che studia i problemi aritmetici utilizzando strumenti di natura geometrica. In questo articolo introduciamo l’argomento studiando il teorema di Pick per il calcolo delle aree di figure piane e le proprietà delle rette del piano che attraversano il reticolo degli interi.
1) Reticoli di punti nel piano \(\mathbf{R}^{2}\)
Ogni punto \(P\) del piano è individuato dalle due coordinate cartesiane: \(P=(x,y)\). Un punto può essere rappresentato da un vettore \(\mathbf{OP}\) che va dall’origine al punto stesso. La somma \(S=P+Q\) di due punti \(P,Q\) è rappresentata dal punto corrispondente alla somma vettoriale dei due vettori \(\mathbf{OP}\) e \(\mathbf{OQ}\).
Definizione 1.1
Un insieme \(L\) di punti del piano \(R^{2}\) è un reticolo (lattice) se soddisfa le seguenti condizioni:
- è un gruppo con l’operazione di somma di punti
- ogni punto è il centro di un cerchio privo di altri punti dell’insieme \(L\)
La seconda condizione implica che i punti di un reticolo sono punti isolati. Per comprendere il significato della prima condizione ricordiamo la definizione di gruppo algebrico:
Definizione 1.2
Un gruppo consiste in un insieme \(G\) sul quale è definita una operazione binaria \(\bullet\), cioè: \(\bullet : G \times G \rightarrow G\), tale che siano soddisfatte le seguenti proprietà:
1) \(a,b \in G \implies a\bullet b \in G\)
2) \(a,b,c \in G \implies a\bullet (b \bullet c) = (a \bullet b) \bullet c\)
3) \( \exists e \in G\) tale che \(a \bullet e = e \bullet a = a \quad \forall a \in G\)
4) \( \forall a \in G \quad \exists b \in G\) tale che \(a\bullet b = b \bullet a = e\)
Nel nostro caso possiamo rappresentare l’operazione binaria con il simbolo di addizione \((+)\).
La prima condizione della definizione del reticolo implica che l’insieme di punti intorno ad un dato punto del reticolo deve avere una forma simile all’insieme dei punti che stanno intorno ad un qualunque altro punto. Ogni reticolo deve contenere il punto \((0,0)\), che rappresenta l’elemento neutro rispetto all’operazione di addizione nel gruppo. Inoltre dati due punti \(P,Q\) del reticolo, allora anche il punto rappresentato dal vettore somma \(\mathbf{OP}+\mathbf{OQ}\) deve appartenere al reticolo.
La definizione di reticolo può essere estesa in modo analogo alla spazio \(\mathbf{R}^{n}\), con \(n >2\).
2) Reticolo piano degli interi
Definizione 2.1
Chiamiamo punto intero (lattice point) un punto del piano \((x,y) \in R^{2}\) se entrambe le coordinate sono numeri interi, cioè se \(x,y \in \mathbf{Z}\). Si chiama reticolo piano degli interi l’insieme dei punti interi del piano. Possiamo indicarlo con il simbolo \(\mathbf{Z}^{2}\).
Esercizio 2.1
Verificare se per ogni numero naturale \(n\) esiste un cerchio che ha al suo interno esattamente \(n\) punti interi. Studiare separatamente il caso del centro in un un punto intero da quello con il centro in un punto non intero.
Per una dimostrazione vedere articolo in questo blog (link).
Esercizio 2.2
Dato il triangolo di vertici interi \((0,0),(x,0),(0,x)\), calcolare il numero dei punti interi del reticolo che si trovano all’interno del triangolo (compresi i lati).
Soluzione: \(\frac{1}{2}(x+1)(x+2)\)
Definizione 2.2 – Triangolo elementare
Un triangolo con vertici interi si dice elementare se non ha punti interi al suo interno.
Esercizio 2.3
Dimostrare che l’area di un triangolo elementare è uguale a \(\frac{1}{2}\).
3) Calcolo delle aree e teorema di Pick
Il teorema di Pick (1859-1942) è uno strumento utile per calcolare l’area di poligoni nel piano che hanno i vertici nei punti interi. Diamo la formulazione seguente del teorema:
Teorema 3.1 – Teorema di Pick
Sia dato un poligono convesso del piano con vertici interi. Sia \(A\) l’area del poligono, \(B\) il numero dei punti interi sulla frontiera, \(I\) il numero dei punti interi contenuti all’interno. Allora vale la seguente formula:
Ricordiamo che un poligono viene detto convesso se, dati due suoi punti qualunque, il segmento che li unisce è interamente contenuto nel poligono stesso.
Esistono varie dimostrazioni del teorema di Pick. La dimostrazione classica procede per gradi, dimostrando il teorema a partire dai casi più semplici:
- rettangolo con vertici interi e lati paralleli agli assi cartesiani
- triangolo rettangolo con vertici interi e cateti paralleli agli assi cartesiani
- triangolo generico con vertici interi
- poligono con vertici interi
Esempio 3.1 – Rettangolo con lati paralleli agli assi
Sia dato un rettangolo di lati \(a,b \in \mathbf{Z}\) con i quattro vertici nei punti del reticolo piano degli interi. Il numero dei punti interni è \((a-1)(b-1)\). Il numero dei punti di frontiera è \(2a+2b\).
Applicando la formula di Pick otteniamo:
Esempio 3.2 – Triangolo rettangolo con cateti paralleli agli assi
Dato un triangolo di vertici \((0,0),(a,0),(0,b)\). Sia \(A\) l’area del triangolo, \(I\) il numero dei punti interni al triangolo, \(B\) il numero dei punti interi sulla frontiera. Verificare la formula di Pick per il calcolo dell’area.
Dimostrazione
Mentre è facile contare il numero dei punti interi sui cateti, sembra difficile determinare quelli contenuti sull’ipotenusa. Tuttavia il problema si può risolvere in questo modo. Indichiamo con \(x\) il numero dei punti interi sulla diagonale, esclusi i due vertici del triangolo. Il numero dei punti presenti sulla frontiera del triangolo è dato da:
Utilizzando il risultato dell’esercizio precedente relativo al rettangolo, possiamo affermare che il numero dei punti interni è il seguente:
\[ I = \frac{(a-1)(b-1)-x}{2} \]Mettendo insieme i risultati, mediante la formula di Pick otteniamo l’area del triangolo:
\[ A = \frac{(a-1)(b-1)-x}{2} + \frac{1}{2}(a + b + x + 1) – 1 = \frac{ab}{2} \]Mediante i due risultati precedenti si può dimostrare il teorema di Pick per tutti i tipi di triangoli. Quindi per dimostrare il teorema per un poligono qualsiasi, si sfrutta sostanzialmente il fatto che un poligono può essere triangolizzato. Vale infatti il seguente teorema:
Teorema 3.2
Ogni poligono convesso semplice con vertici interi, ha almeno una triangolazione, cioè una decomposizione in triangoli che hanno un vertice in comune.
Esercizio 3.1
Dimostrare che è impossibile costruire un triangolo equilatero con i tre vertici interi.
Dimostrazione
L’area di un triangolo equilatero con i tre vertici interi \(\{(0,0),(x_{1},y_{1}),(x_{2},y_{2})\}\) è uguale a \(A= \frac{\sqrt{3}}{4}(x_{1}^{2}+ y_{1}^{2}) \), che è un numero irrazionale. D’altra parte se i tre vertici fossero interi allora per il teorema di Pick l’area sarebbe un numero razionale.
Esercizio 3.2 – (R. Honsberger)
Un quadrato di lato \(n\) viene lanciato in modo casuale in un piano. Dimostrare che non può mai contenere un numero di punti interi maggiore di \((n + 1)^{2}\).
Dimostrazione
I punti di frontiera di un quadrato possono essere al massimo \(4n\). Applicando il teorema di Pick otteniamo
Il numero totale dei punti interi interni e di frontiera coperti dal quadrato è \(I+B\), e quindi abbiamo:
\[ \begin{split} I+B &=I + \frac{B}{2}+ \frac{B}{2}= n^{2}+ \frac{B}{2}+1 \le n^{2}+2n+1=(n+1)^{2} \end{split} \]Esercizio 3.3
Sia dato il rombo con centro nell’origine e vertici \((\pm b,0\)), (\((0,\pm a)\), con \(a,b\) interi positivi. Sia \(d=(a,b)\) il massimo comune denominatore. Utilizzare il teorema di Pick per determinare \(I\), il numero dei punti interi che sono interni al rombo.
Risposta: \(I = 2ab -2d+1\)
Nota 3.1
Il teorema di Pick può essere dimostrato anche utilizzando la formula di Eulero relativa ai grafi, secondo la quale per un grafo connesso e planare \(G\), con \(V\) vertici, \(E\) lati e \(F\) facce, vale la seguente relazione:
Per i dettagli della dimostrazione che utilizza la formula di Eulero vedere [1].
Nota 3.2
Il teorema di Pick non si estende nello spazio a tre dimensioni per calcolare il volume dei solidi. Nel 1957 Reeve ha proposto un poliedro, chiamato poliedro di Reeve, di vertici \((0,0,0),(1,0,0),(0,1,0),(1,1,h)\) con \(h\) intero positivo. Questo poliedro può assumere valori diversi del volume senza cambiare il numero dei punti interi e di frontiera. Per maggiori dettagli vedere ad esempio [2].
Teorema 3.3 – Arkinstall
Un pentagono convesso con vertici interi, deve contenere almeno un punto intero al suo interno.
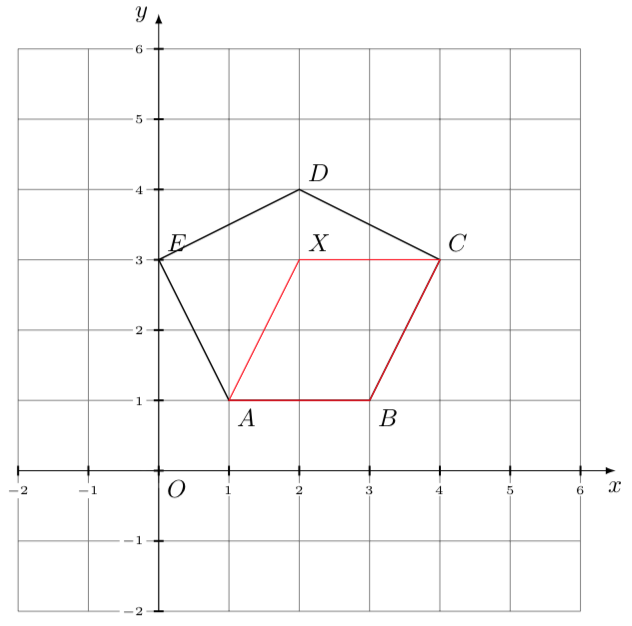
Dimostrazione
Dato un pentagono convesso, la somma degli angoli interni è uguale a \(5\pi – 2\pi=3\pi\). Consideriamo le \(5\) coppie di angoli interni adiacienti. La somma totale degli angoli è \(6\pi\) e quindi ci deve essere una coppia di angoli (diciamo \(A,B\)) la cui somma è maggiore di \(\pi\). Costruiamo il parallelogramma \(ABCX\), dove \(C\) non è più lontano di \(E\) dal segmento \(AB\). Allora il punto \(X\) del parallelogramma è interno al pentagono, e inoltre è intero, in quanto lo sono gli altri \(3\) punti \(A,B,C\).
4) Il polinomio di Ehrhart
Una variante del teorema di Pick consiste nel calcolare il numero dei punti interi contenuti in un regione convessa, invece dell’area. Sia \(P\) un poligono piano convesso con i vertici interi. Dato un intero positivo \(t\) definiamo il seguente insieme \(t \cdot P\):
\[ t \cdot P = \{(tx,ty) | (x,y) \in P \} \]Il poligono \(t\cdot P\) è il poligono iniziale \(P\) scalato del fattore intero \(t\).
Teorema 4.1 – Ehrhart (1906-2000)
Dato un poligono convesso \(P\) nel piano con vertici interi. Sia \(A\) l’area del poligono \(P\), \(B\) il numero dei punti interi sulla frontiera di \(P\), \(P(t)\) il numero totale dei punti interi contenuti nel poligono \(t\cdot P\) (compresi i punti di frontiera). Allora vale la seguente formula:
Il teorema di Pick corrisponde al caso \(t=1\). Il polinomio \(P(t)\) viene chiamato polinomio di Ehrhart. L’aspetto interessante del teorema è che basta conoscere l’area di \(P\) e il numero dei punti interi sulla sua frontiera, per poter calcolare il numero di punti sulla regione \(t\cdot P\), per ogni intero positivo \(t\).
Esempio 4.1
Dato un triangolo di lati \(a=3,b=1\). Dimostrare che \(P(t)= \frac{3}{2}t^{2}+ \frac{5}{2}t+1\).
Per i dettagli della dimostrazione completa dei teoremi di Pick e di Ehrard vedere ad esempio [3].
5) Retta passante per i punti di un reticolo piano
Ricordiamo il seguente teorema di Bézout, la cui dimostrazione si trova in ogni testo di teoria elementare dei numeri.
Teorema 5.1 – Bézout
Siano dati due interi \(a,b\) tali che \((a,b)=d\). Allora esistono interi \(s,t\) tali che
Introduciamo ora il concetto di equazione diofantea.
5.1) Equazioni diofantee
Consideriamo la seguente equazione lineare nelle incognite \(x,y\), che rappresenta una retta del piano:
\[ ax + by = c \quad \text{ \(a,b,c \in \mathbf{Z}\)} \]L’equazione si dice diofantea se interessa risolverla limitatamente alle soluzioni intere, cioè con \((x,y)\) entrambi interi. Il nome diofanteo è in onore del matematico greco Diofanto, che visse in Alessandria di Egitto intorno al 250 d.C. Dal punto di vista geometrico le soluzioni sono i punti del reticolo degli interi attraversati dalla retta.
In base al teorema di Bézout l’equazione ha soluzione intera se e solo se \(d=(a,b)|c\). Possiamo enunciare il seguente teorema che è facile da verificare:
Teorema 5.2
Se esiste una soluzione \((x_{0},y_{0})\), allora ne esistono infinite date dalle seguenti formule:
Esercizio 5.1
Risolvere le seguenti equazioni diofantee:
Soluzione
Come esempio risolviamo la seconda. Anche se in questo caso è banale, troviamo il massimo comune divisore mediante l’algoritmo euclideo:
Il massimo comune divisore è \((60,33)=3\), il quale divide il termine noto \(9\) dell’equazione. Quindi sappiamo che l’equazione ha soluzioni intere. Per trovarle ripercorriamo l’algoritmo di Euclide al contrario:
\[ \begin{split} 3 = 27 – 4 \cdot 6 = 27 – 4(33-27) = 5 \cdot 27 – 4 \cdot 33 \\ =5(60-33) – 4 \cdot 33 = 5 \cdot 60 – 9 \cdot 33 \\ \end{split} \]Moltiplichiamo per \(5\) e otteniamo una soluzione particolare \((15,-27)\). Le altre si ottengono con la formula del teorema: \((x=15 + 11k;y=-27-20k)\).
5.2) Rette con pendenza razionale
Ricordiamo che nel piano l’equazione di una retta può essere scritta nella seguente forma:
\[ y = mx + q \]dove \(m\) è il coefficiente angolare che rappresenta la pendenza della retta. Precisamente si ha questa relazione:
\[ m = \tan \theta \]dove \(\theta\) è l’angolo che la retta forma con l’asse delle ascisse.
Teorema 5.3
Data una retta di equazione \(y = \frac{a}{b}x + \frac{r}{s}\), con \((a,b)=(r,s)=1\) e \(s|b\). Se la retta passa per un punto intero del reticolo \((x_{0},y_{0})\), allora passa per infiniti altri punti del reticolo. Precisamente i seguenti punti:
per \(k= 0,\pm 1,\pm2, \cdots\)
Dimostrazione
Nell’equazione è stato messo il termine noto razionale \(\frac{r}{s}\), in quanto se il coefficiente angolare \(\frac{m}{n}\) è razionale e la retta deve passare per un punto intero del reticolo, allora necessariamente il termine noto deve essere razionale. Partendo dall’equazione e facendo il minimo comune multiplo abbiamo:
Questo implica che deve essere \(s|b\) in quanto \((r,s)=1\). Se esiste un punto intero \((x_{0},y_{0})\) sulla retta, allora per il teorema 5.2 ne esistono infiniti; precisamente tutti i punti \((x,y)\) tali che:
\[ \begin{split} x_{k} = x_{0} + kb \\ y_{k} = y_{0} + ka\\ \end{split} \]5.3) Rette con pendenza irrazionale
Teorema 5.4
Sia data la seguente equazione di una retta:
dove \(a\) è un numero irrazionale. Allora o la retta non passa attraverso alcun punto intero, oppure passa al massimo attraverso un solo punto intero.
Dimostrazione
Se passasse attraverso due punti interi \(A(x_{1},y_{1}),B(x_{2},y_{2})\), allora il coefficiente angolare della retta \(\frac{(y_{2} – y_{1})}{(x_{2}-x_{1})}\), e quindi la pendenza, sarebbe un numero razionale.
Esercizio 5.2
Dare un esempio di retta con pendenza irrazionale che non passa attraverso alcun punto intero, e un esempio di retta che passa attraverso un unico punto intero.
Per determinare quali sono i valori dell’angolo \(\theta\) tali che \(\tan \theta\) è un numero irrazionale, ricordiamo il seguente teorema:
Teorema 5.5 – Lambert (1728-1777)
Sia \(a = \tan \theta\). Allora \(a\) è irrazionale se \(\theta\) in radianti è un numero razionale non nullo. Se utilizziamo i gradi, allora \(a\) è irrazionale se \(\theta\) è un numero razionale non nullo, ad eccezione dei valori \(45+90k, k=0,\pm 1, \pm 2, \cdots\).
Per una dimostrazione vedere ad esempio [4].
Vale anche il seguente importante teorema che ci limitiamo ad enunciare:
Teorema 5.6
Sia data una retta \(y=ax+b\), dove \(a\) è un numero irrazionale e \(b\) un numero reale. Allora per ogni fissato \(\epsilon >0\), da entrambe le parti della retta esistono infiniti punti del reticolo piano degli interi che hanno distanza dalla retta minore di \(\epsilon\).
Per una dimostrazione vedere il testo [5] oppure l’articolo [6].
Conclusione
La relazione fra il reticolo degli interi, la geometria e la teoria dei numeri è ricca di applicazioni. Tra gli argomenti più interessanti ricordiamo i seguenti:
- il problema del cerchio di Gauss
- i divisori di un intero e il metodo dell’iperbole di Dirichlet
- il teorema di Blichfeldt
- il teorema di Minkowski
Questi argomenti saranno oggetto di studio in successivi articoli di questo blog.
Bibliografia
[1]Aigner, Ziegler, Hofmann – Proofs from the Book (Springer)
[2]Beck, Matthias, Robins, Sinai – Computing the Continuous Discretely (Springer), pag. 72
[3]Beck, Matthias, Robins, Sinai – Computing the Continuous Discretely (Springer)
[4]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991)
[5]Erdos, Suranyi – Topics in the theory of numbers (Springer)
[6]A. Kempner – A Theorem on Lattice-Points (Annals of Mathematics Second Series, Vol. 19, No. 2, Dec. 1917)

0 commenti