Il questo articolo studieremo un importante risultato, chiamato lemma o teorema di Burnside (1852-1927), che è molto utile per contare le configurazioni di un oggetto, tenendo conto delle simmetrie. In realtà il teorema era stato dimostrato in precedenza da Frobenius (1849-1917) e ancora prima da Cauchy (1789-1857 ), per cui viene chiamato anche teorema di Cauchy-Frobenius. Lo stesso Burnside attribuì questo risultato a Frobenius e inserì il lemma nel suo libro di algebra ‘On the Theory of Groups of Finite Order’, pubblicato inizialmente nel \(1897\).
1) Simmetrie e conteggio
Vediamo alcuni esempi per illustrare il problema.
Esempio 1.1
Supponiamo di voler colorare un cubo di \(6\) facce avendo a disposizione \(n\) colori. Per ogni faccia possiamo scegliere tra \(n\) colori e quindi il numero delle colorazioni possibili è \(n^{6}\). Tuttavia, molte delle colorazioni sono equivalenti fra loro se ruotiamo il cubo in modo opportuno. Il problema è quindi quello di determinare le colorazioni che sono effettivamente distinte fra loro, e non possono essere sovrapposte con alcuna rotazione. È evidente che anche per valori piccoli di \(n\) il conteggio manuale delle colorazioni distinte è molto complicato e diventa impossibile per valori grandi di \(n\).
Esempio 1.2
Supponiamo di avere una collana nella quale sono inserite \(4\) palline. Se abbiamo solo due colori, rosso e nero, quante configurazioni distinte possiamo creare? Consideriamo distinte due colorazioni se non è possibile sovrapporle mediante una rotazione.
In questo caso il problema è semplice e con un pò di riflessione possiamo determinare tutte le diverse configurazioni:
Esempio 1.3
Determinare in quanti modi distinti si possono colorare le caselle di una scacchiera \(8 \times 8\) con due colori.
Oppure il problema più generale di colorare una scacchiera \(2k \times 2k\) con \(n\) colori, con \(n \gt 2\).
Tranne nei casi più semplici, la risoluzione di questi problemi con il metodo diretto di conteggio manuale delle distinte configurazioni non è praticabile.
Il teorema di Burnside è uno strumento utile per risolvere questi tipi di problemi. Per comprendere la dimostrazione del teorema è necessario in primo luogo dare una definizione rigorosa del concetto di simmetria e di trasformazioni di un oggetto. In termini generici possiamo dire che per definire una simmetria di un oggetto dobbiamo specificare due cose:
- una proprietà di un oggetto che vogliamo rimanga invariata (ad esempio la forma geometrica, la struttura, la distribuzione di colori, ecc.);
- un insieme di trasformazioni permesse che agiscono sull’oggetto.
Una volta specificati questi due punti, si individuano le trasformazioni che lasciano invariata la proprietà desiderata.
La teoria dei gruppi, su cui si basa il teorema di Burnside, permette una definizione rigorosa del concetto di simmetria. Nel seguito riportiamo alcune delle definizioni e proprietà della teoria dei gruppi, necessarie per comprendere la dimostrazione del teorema. Per approfondire la teoria dei gruppi vedere ad esempio [1].
2) Richiami di teoria dei gruppi
La teoria dei gruppi è una branca della matematica molto bella e molto vasta, che ha applicazioni importanti in molti settori della scienza, tra cui la fisica e la chimica.
Dato un insieme \(G\), un’operazione binaria su \(G\) è una funzione che ad ogni coppia di elementi \(a,b \in G\) associa un elemento di \(G\). Possiamo indicare l’operazione binaria con vari simboli. In genere utilizzeremo la notazione \(a \cdot b\), mentre nel caso di gruppi additivi utilizzeremo la notazione \(a + b\).
Definizione 2.1
Un gruppo è una coppia ordinata \((G,\cdot)\) dove \(G\) è un insieme e \(\cdot\) è un’operazione binaria su \(G\), che ad ogni coppia di elementi di \(G\) associa un elemento di \(G\):
Esso verifica le seguenti proprietà (o assiomi):
- proprietà associativa: \(a \cdot (b \cdot c)=(a \cdot b) \cdot c\)
- elemento neutro: esiste un elemento \(e\) di \(G\) tale che \(a \cdot e=a\) per ogni \(a \in G\)
- elemento inverso: per ogni elemento \(a \in G\) esiste un elemento \(b\) tale che \(a \cdot b=e\)
In genere si aggiunge un quarto assioma, imponendo che l’elemento dell’operazione binaria \(a \cdot b\) debba appartenere all’insieme \(G\); tuttavia questo assioma è chiaramente superfluo, in quanto è già implicito nella definizione di operazione binaria.
Un gruppo si dice commutativo o abeliano, in onore del matematico norvegese N.H. Abel (1802-1829), se risulta
L’elemento neutro \(e\) viene indicato in genere con \(1\) nel caso di gruppi moltiplicativi e con \(0\) nel caso di gruppi additivi. L’inverso di un elemento \(a\) viene indicato con \(a^{-1}\) nel caso di gruppi moltiplicativi e con \(-a\) nel caso di gruppi additivi.
Si chiama ordine di un gruppo il numero di elementi dell’insieme \(G\) e si indica con il simbolo \(|G|\), oppure con \(o(G)\).
Esempio 2.1
Consideriamo il seguente sottoinsieme dei numeri complessi \(G=\{1,-1,i,-i\}\), dove \(i\) è l’unità immaginaria tale che \(i^{2}=-1\). La struttura di gruppo rispetto all’operazione di moltiplicazione fra numeri complessi può essere rappresentata mediante la seguente tabella di Cayley, così chiamata in onore del matematico inglese Arthur Cayley (1821-1895):
Il simbolo \(\times\) indica l’operazione di moltiplicazione fra numeri complessi. È facile verificare che sono soddisfatti gli assiomi di gruppo. L’elemento neutro rispetto alla moltiplicazione è il numero \(1\).
Esempio 2.2
L’insieme degli interi \(\mathbb{Z}\) con l’operazione di addizione è un gruppo additivo infinito. Con l’operazione di moltiplicazione non è un gruppo, in quanto l’inverso moltiplicativo di un intero \(x\) non esiste, tranne nel caso \(x= \pm 1\).
L’insieme dei numeri naturali non è un gruppo con l’operazione binaria di addizione in quanto non esistono gli opposti dei numeri naturali. Naturalmente non è un gruppo neanche rispetto alla moltiplicazione.
Esempio 2.3
L’insieme dei numeri razionali \(\mathbb{Q}\) con l’operazione di addizione è un gruppo additivo.
Con l’operazione di moltiplicazione non è un gruppo in quanto il numero \(0\) non ha un inverso. Tuttavia se togliamo lo zero, allora l’insieme \(\mathbb{Q} {\setminus} \{0\}\) è un gruppo moltiplicativo.
Considerazioni simili si possono fare per gli insiemi dei numeri reali \(\mathbb{R}\) e dei numeri complessi \(\mathbb{C}\).
Esempio 2.4 – Il gruppo diedrale
Dato un poligono regolare di \(n\) lati, il gruppo diedrale \(D_{n}\) di ordine \(2n\) è costituto da \(n\) rotazioni di \(\dfrac{2 \pi k}{n}\) radianti, con \(k=0,1,\cdots,n-1\), e da \(n\) riflessioni lungo gli assi di simmetria del poligono, cioè rette che passano per il centro e hanno un angolo di \(\dfrac{\pi k}{n}\) radianti con l’asse delle ascisse.
Senza perdere generalità possiamo considerare un poligono regolare di \(n\) vertici, inscritto nel cerchio unitario di centro \((0,0)\). Per semplicità supponiamo di identificare i vertici con i simboli \(v_{1}, \cdots,v_{n}\), procedendo dal primo di coordinate cartesiane \((1,0)\) e andando in senso antiorario.
L’operazione di gruppo è la composizione delle rotazioni e delle riflessioni. Tutte le rotazioni si ottengono applicando ripetutamente la rotazione base di \(\dfrac{2\pi}{n}\) radianti. La composizione di due rotazioni o di due riflessioni è una rotazione, mentre la composizione di una rotazione e una riflessione è una riflessione.
Esercizio 2.1
Indichiamo con \(\mathbb{Z}_{n}\) l’insieme costituito dalle classi residuo modulo \(n\). L’insieme contiene \(n\) elementi o classi. La classe relativa ad un intero \(a\) contiene tutti gli interi che sono congruenti ad \(a\), cioè
dove il simbolo \(\equiv\) indica la relazione di congruenza. Sostanzialmente la classe \(\overline{a}\) contiene tutti gli interi che danno lo stesso resto nella divisione per \(n\). Ovviamente sono possibili solo \(n\) resti diversi. Ad esempio la classe \(\overline{0}\) contiene lo zero e tutti i multipli positivi e negativi di \(n\).
Sull’insieme delle \(n\) classi definiamo questa operazione binaria di addizione:
Dimostrare che l’operazione è ben definita, cioè il risultato non dipende dall’elemento che si prende come rappresentante di una data classe. Quindi dimostrare che con questa operazione l’insieme diventa un gruppo abeliano.
Definizione 2.2
Un sottoinsieme \(H\) di \(G\) è un sottogruppo di \((G,\cdot)\) se i suoi elementi formano un gruppo con la stessa operazione binaria.
Ad esempio l’insieme degli interi pari è un sottogruppo del gruppo degli interi con l’operazione di addizione. Naturalmente ciò non vale per l’insieme degli interi dispari.
Esercizio 2.2
Dimostrare che un sottoinsieme \(H\) è un sottogruppo di \((G,\cdot)\) se e solo se risulta
Definizione 2.3 – Classe laterale
Sia \(H\) un sottogruppo del gruppo \(G\) e \( a \in G\). Si chiama classe laterale destra di \(H\) con rappresentante \(a\) l’insieme
In modo simile si definiscono le classi laterali sinistre. Naturalmente se il gruppo \(G\) è abeliano i due insiemi coincidono.
Nella notazione additiva la classe laterale destra viene denotata con \(H+a =\{h+a| h \in H\}\).
Si può dimostrare il seguente teorema:
Teorema 2.1
L’insieme delle classi laterali destre forma una partizione di \(G\); cioè, date due classi laterali destre qualsiasi, o sono identiche oppure non hanno alcun elemento in comune.
Lo stesso teorema per le classi laterali sinistre.
Dal teorema precedente deriva l’importante teorema di Lagrange per i gruppi finiti:
Teorema 2.2 – Lagrange
Se \(H\) è un sottogruppo di un gruppo finito \(G\), allora
Quindi l’ordine di un sottogruppo di un gruppo finito divide l’ordine del gruppo. Il valore di \(n\) si chiama l’indice di \(H\) in \(G\).
Definizione 2.4 – Ordine di un elemento
Dato un gruppo \(G\) e un elemento \(a \in G\), si chiama ordine di \(a\) il più piccolo intero positivo \(m\) tale che \(a^{m}=e\). Se un tale intero positivo non esiste, si dice che l’elemento \(a\) ha ordine infinito. Usiamo la notazione \(o(a)\) per l’ordine di \(a\).
Esercizio 2.3
Supponiamo che \(G\) sia un gruppo finito e \(a \in G\). Dimostrare che l’insieme
è un sottogruppo di \(G\). Tale sottogruppo si chiama sottogruppo ciclico generato da \(a\) e si indica con il simbolo \(\mathopen {<}a\mathclose{>}\).
Nel caso di gruppi abeliani si usa la notazione additiva: ad esempio \(a^{3}=a\cdot a \cdot a\) diventa \(3a=a+a+a\).
Esercizio 2.4
Dimostrare che il gruppo additivo degli interi è generato dal numero \(1\), cioè \(\mathbb{Z}=\mathopen{<}1\mathclose{>}\).
2.1) Isomorfismo di gruppi
Definizione 2.5
Siano \(G_{1},G_{2}\) due gruppi e sia data una funzione \(\phi: G_{1} \to G_{2}\). La funzione \(\phi\) si chiama omomorfismo se risulta
I due gruppi possono avere operazioni del tutto diverse fra loro. Nella definizione di omomorfismo per semplicità si usa lo stesso simbolo a sinistra e a destra. Tuttavia, è bene sottolineare che nella parte a sinistra dell’equazione l’espressione \(a \cdot b\) indica l’operazione binaria del gruppo \(G_{1}\), mentre nella parte destra l’espressione \(\phi(a) \cdot \phi(b)\) indica l’operazione binaria del gruppo \(G_{2}\).
Se la funzione \(\phi\) è iniettiva e suriettiva allora viene chiamata isomorfismo, e i due gruppi si dicono isomorfi. Per indicare che due gruppi sono isomorfi si usa la notazione \(G_{1} \cong G_{2}\).
Esercizio 2.5
Dimostrare che la relazione di isomorfismo fra gruppi è una relazione di equivalenza.
In base all’esercizio precedente la relazione di isomorfismo crea una partizione dell’insieme dei gruppi. La teoria dei gruppi studia le proprietà che rimangono invariate rispetto alla relazione di isomorfismo. Esempi di proprietà invarianti sono l’ordine del gruppo o il fatto di essere abeliano. Dal punto di vista della teoria dei gruppi tutti i gruppi isomorfi fra loro sono equivalenti, anche se si tratta di insiemi e operazioni del tutto diversi.
Esempio 2.5
Un esempio importante di isomorfismo fra gruppi è il seguente:
dove \((\mathbb{R},+)\) è il gruppo additivo dei numeri reali, mentre \((\mathbb{R}^{+},\cdot)\) è il gruppo moltiplicativo dei numeri reali positivi.
Infatti abbiamo \(\phi(x+y)=e^{x+y}=e^{x}e^{y}=\phi(x)\phi(y)\), e la corrispondenza è chiaramente biunivoca.
3) Il gruppo simmetrico
3.1) Permutazioni
Sia \(X=\{x_{1},x_{2},\cdots,x_{n}\}\) un insieme di \(n\) elementi. Una permutazione sull’insieme \(X\) è una corrispondenza biunivoca dell’insieme in se stesso. Possiamo rappresentare una permutazione mediante una matrice:
\[ \begin{pmatrix} x_{1} & x_{2} & \cdots & x_{n} \\ x_{i_{1}} &x_{i_{2}} & \cdots & x_{i_{n}}\\ \end{pmatrix} \]Risulta più semplice indicare gli elementi di \(X\) con i numeri naturali: \(X=\{1,2,\cdots,n\}\); quindi la permutazione viene rappresentata con la seguente matrice:
\[ \begin{pmatrix} 1 & 2 & \cdots & n \\ a_{1} & a_{2} & \cdots & a_{n} \\ \end{pmatrix} \]Esempio 3.1
Un esempio di permutazione sull’insieme \(X=\{1,2,3,4,5,6\}\) è il seguente:
Chiaramente per un insieme di \(n\) elementi esistono \(n!\) permutazioni distinte. Sull’insieme delle permutazioni di un insieme \(X\) è possibile definire l’operazione binaria di composizione (o prodotto) di permutazioni. Date due permutazioni \(\alpha\) e \(\beta\), la composizione viene indicata con la notazione \(\alpha \circ \beta\), con la convenzione che prima agisce la \(\beta\) e poi la \(\alpha\).
Esempio 3.2
Siano date le seguenti due permutazioni:
Il prodotto delle due permutazioni è quindi
\[ \alpha \cdot \beta = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \\ \end{pmatrix} \circ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 2 & 4 \\ \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 2 & 1 & 4 \\ \end{pmatrix} \]Un tipo di permutazione importante è il ciclo, che sposta in modo ciclico alcuni elementi e tiene fissi gli altri. Ad esempio:
\[ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 3 & 5 & 1 \\ \end{pmatrix} \]Un ciclo può essere rappresentato anche con una singola riga, nella quale a ogni indice si associa quello successivo e all’ultimo si associa il primo: \(\{1,2,4,5\}\).
Si può dimostrare che qualunque permutazione può essere rappresentata in modo univoco come composizione di cicli disgiunti. Ad esempio la permutazione dell’esempio 3.1 è equivalente alla composizione dei seguenti cicli: \(\{1,2,3,5\}\{4,6\}\).
Una permutazione si dice ciclica se può essere rappresentata con un solo ciclo.
3.2) Il gruppo simmetrico
Sia \(X=\{1,2,\cdots,n\}\) un insieme finito di ordine \(n\). Il gruppo simmetrico su \(X\) è costituito da tutte le permutazioni possibili su \(X\). L’operazione binaria di gruppo consiste nella composizione di due permutazioni.
Il gruppo simmetrico viene indicato con il simbolo \(\text{Sym}(X)\) o più semplicemente nel caso finito con \(S_{n}\).
L’elemento neutro del gruppo è la funzione identità, che lascia invariato l’ordine degli elementi. Viene indicata con il simbolo \(\epsilon\). Nella notazione ciclica la permutazione identità è \(\epsilon=(1)(2)\cdots(n)\), cioè il prodotto di \(n\) cicli disgiunti.
Esempio 3.3
Se \(X=\{1,2,3\}\), il gruppo simmetrico è
Esercizio 3.1
Dimostrare che per l’insieme \(S_{n}\) con l’operazione di composizione di permutazioni sono verificati gli assiomi di gruppo.
Data una permutazione \(\sigma \in S_{n}\) definiamo la permutazione \(\sigma ^{i}, i \in \mathbb{Z}, i \ge 0\), ottenuta componendo la \(\sigma\) con se stessa \(i\) volte. In particolare \(\sigma^{0}=\epsilon\).
Esercizio 3.2
Dimostrare che l’insieme \(\{\sigma ^i| i\ge 0\}\) è un sottogruppo di \(S_{n}\). Questo sottogruppo viene chiamato il sottogruppo generato da \(\sigma\) e viene indicato con il simbolo \(\mathopen{<}\sigma\mathclose{>}\).
3.3) Gruppi di trasformazione e teorema di Cayley
Un teorema fondamentale relativo ai gruppi finiti è stato dimostrato dal matematico inglese Cayley (1821-1895).
Teorema 3.2 – Teorema di Cayley
Ogni gruppo finito è isomorfo ad un gruppo di permutazioni.
Dimostrazione
Il concetto chiave è che ad ogni elemento \(g \in G\) possiamo associare una permutazione dell’insieme \(G\) stesso. La permutazione associata all’elemento \(g\) è la la funzione \(\phi_{g}: x \to g \cdot x\). È facile verificare che la funzione \(\phi_{g}\) è un omomorfismo. Inoltre è una corrispondenza biunivoca e quindi un isomorfismo.
Il teorema di Cayley può essere generalizzato anche ai gruppi infiniti. Il gruppo simmetrico \(\text{Sym}(X)\) di un insieme infinito \(X\) è l’insieme delle funzioni \(F: X \to X\) iniettive e suriettive. È facile verificare che sono soddisfatti gli assiomi di gruppo con l’operazione di composizione. L’elemento neutro è la funzione identità \(I(x)=x \quad \forall x \in X\).
Il teorema di Cayley afferma sostanzialmente che ogni gruppo è isomorfo ad un gruppo di trasformazioni biunivoche.
4) Azioni di un gruppo, orbite e stabilizzatori
4.1) Azione di un gruppo
Il concetto base dell’azione di un gruppo è che gli elementi di un gruppo possono essere visti come permutazioni che agiscono su un insieme. La corrispondenza è tale che il prodotto di due elementi del gruppo corrisponde alla composizione delle permutazioni relative.
Dati due elementi \(g,h\) di un gruppo, per semplicità d’ora in poi indicheremo l’operazione di gruppo con \(gh\) al posto di \(g \cdot h\).
Definizione 4.1
Una azione di un gruppo \(G\) su un insieme \(X\) è una funzione \(f: G \times X \to X\) tale che:
Il simbolo \(1\) rappresenta l’elemento identità del gruppo \(G\).
Per semplicità in genere si usa la notazione \(g \cdot x\) per indicare l’azione \(f(g,x)\). Le due proprietà precedenti diventano quindi
La notazione \( g \cdot x\) non va intesa come moltiplicazione fra un elemento di \(G\) e un elemento di \(X\), ma indica semplicemente l’effetto di \(g\) (o meglio della permutazione associata a \(g\)) sull’elemento \(x \in X\).
Si può dare una definizione equivalente di azione di un gruppo:
Definizione 4.2
Sia \(G\) un gruppo e \(X\) un insieme. Indichiamo con \(\text{Sym}(X)\) il gruppo di tutte le permutazioni di \(X\). Se \(X\) è finito allora \(\text{Sym}(X)=S_{n}\) dove \(n=|X|\). Si dice che il gruppo \(G\) agisce sull’insieme \(X\) se esiste un omomorfismo
La funzione \(\phi\) quindi associa ad ogni elemento \(g \in G\) una permutazione \(\pi_{g} \in \text{Sym}(X)\), tale che vale la seguente condizione:
\[ \pi_{gh} = \pi_{g} \circ \pi_{h} \quad \forall g,h \in G \]Si può dimostrare che le due definizioni sono equivalenti.
Esempio 4.1 – L’azione regolare
Dal teorema di Cayley sappiamo che ogni gruppo agisce su se stesso con la funzione \(x \to gx\), cioè la permutazione che trasforma \(x\) in \(gx\). L’azione regolare è così definita: \(g \cdot x =gx\), dove \(gx\) è la normale operazione binaria su due elementi del gruppo \(G\). In questo caso l’omomorfismo è iniettivo. Si tratta quindi di una azione del gruppo \(G\) su se stesso.
Esempio 4.2
Ogni elemento del gruppo diedrale \(D_{n}\) è una rotazione o oppure una riflessione, cioè è un moto rigido del poligono regolare. Per determinare la posizione del poligono basta esaminare la posizione degli \(n\) vertici, ognuno identificato con una etichetta, ad esempio \(1,2,\cdots, n\). In questo caso possiamo quindi dire che il gruppo diedrale agisce sugli elementi dell’insieme \(\{1,2,\cdots,n\}\).
Esercizio 4.1
Consideriamo l’insieme \(X=\{1,2,\cdots,n\}\) e il gruppo simmetrico \(S_{n}\). Per ogni permutazione \(\pi \in S_{n}\) definiamo la seguente azione di \(S_{n}\) su \(X\):
Ad esempio se
\[ \pi = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 3 & 5 & 6 & 1 & 4 \\ \end{pmatrix} \]allora \(\pi \cdot 3 = 5\). Verificare che si tratta di un’azione del gruppo simmetrico sull’insieme \(X\).
4.2) Orbita
Data un’azione \(\cdot: G \times X \to X\) di un gruppo \(G\) su un insieme \(X\), definiamo la seguente relazione sull’insieme \(X\):
\[ x \sim y \iff y = g \cdot x \quad \text{ per qualche } g \in G \]È facile dimostrare che la relazione sopra definita è una relazione di equivalenza, e quindi induce una partizione dell’insieme \(X\) in classi di equivalenza. Per ogni \( x \in X\) la classe di equivalenza associata, indicata con \(\text{Orb}(x)\) e chiamata orbita di \(x\), è
\[ \begin{array}{l} \text{Orb}(x) = \{y \in X: y= g\cdot x \ , \quad g \in G\} \\ \end{array} \]L’orbita di \(x\) rispetto a \(G\) è quindi un sottoinsieme di \(X\), contenente tutte le possibili immagini di \(x\), sotto l’azione degli elementi di \(G\).
Esempio 4.3
Sia \(X=\{v_{1},v_{2},\cdots,v_{n}\}\) l’insieme dei vertici di un poligono regolare di \(n\) lati. Indichiamo con \(G\) il gruppo delle rotazioni antiorarie intorno al centro del poligono, di ampiezza \(\dfrac{2\pi k}{n}\) con \(k=0,1,\cdots,n-1\). Prendiamo un vertice \(v_{k} \in X\). La sua orbita è tutto l’insieme \(X\), in quanto con le rotazioni il vertice può raggiungere tutti gli altri elementi dell’insieme \(X\).
Esempio 4.4
Nel gioco degli scacchi, un alfiere che si trova in una casella qualsiasi può raggiungere tutte le altre caselle con lo stesso colore, eseguendo le mosse permesse all’alfiere.
Una torre con il suo gruppo di mosse può raggiungere tutte le caselle, quindi la sua orbita è tutta la scacchiera.
Esercizio 4.2
Dimostrare che \(x \in \text{Orb}(x)\). Inoltre, dimostrare che
4.3) Insieme dei punti fissi e stabilizzatore
Definizione 4.3 – Insieme dei punti fissi
Dati un’azione \(\cdot: G \times X \to X\) di un gruppo \(G\) su un insieme \(X\) e un elemento \(g \in G\). L’insieme dei punti fissi rispetto a \(g\), indicato con \(X_{g}\), è
Definizione 4.4 – Stabilizzatore
L’insieme \(G_{x}\), chiamato lo stabilizzatore di \(x\) in \(G\), è l’insieme delle permutazioni di \(G\) che hanno \(x\) come punto fisso:
Esempio 4.5
Consideriamo l’insieme \(X=\{1,2,3,4\}\) e il gruppo simmetrico \(S_{4}\) che agisce su \(X\), come descritto nell’esercizio 4.1. Calcoliamo \(G_{2}\), lo stabilizzatore dell’elemento \(2\) di \(X\). Naturalmente la permutazione identità \(\epsilon \in G_{2}\), in quanto \(\epsilon(k)=k, \forall k \in X\). Usando la notazione ciclica si verifica che le permutazioni che appartengono allo stabilizzatore sono le seguenti: \(G_{2}=\{\epsilon,(1,3),(1,4),(3,4),(1,3,4),(1,4,3)\}\).
Esercizio 4.3
Dimostrare che lo stabilizzatore \(G_{x}\) è un sottogruppo di \(G\).
Esercizio 4.4
Consideriamo la seguente azione di un gruppo \(G\) su se stesso, chiamata azione di coniugazione:
Verificare le seguenti formule:
\[ \begin{array}{l} \text{Orb}(x) = \{x\} \\ G_{x} = G \\ \end{array} \]Esercizio 4.5
Dimostrare che
Dimostrazione
\[ \begin{array}{l} \sum\limits_{x \in X }|G_{x}|= \sum\limits_{x \in X }|\{g \in G: g\cdot x=x\}|= \\ \left|\{(g,x): g \in G, x \in X, g \cdot x=x \}\right|= \\ \sum\limits_{g \in G }|\{x \in X: g\cdot x=x\}|=\sum\limits_{g \in G }|X_{g}| \end{array} \]Teorema 4.1 – Teorema orbita-stabilizzatore
Sia \(G\) un gruppo finito che agisce su un insieme \(X\). Allora per ogni \(x \in X\) abbiamo
Dimostrazione
Abbiamo \(\text{Orb}(x)=\{g \cdot x: g \in G\}\). Se \(g \cdot x=h \cdot x\) allora \(g^{-1}h \cdot x=x\) e quindi \(g^{-1}h \in G_{x}\). Questo implica che \(h=ga\) con \(a \in G_{x}\), quindi \(h\) appartiene alla classe laterale sinistra di \(G_{x}\) determinata da \(g\). In altre parole \(g\) e \(h\) determinano la stessa classe laterale sinistra dello stabilizzatore \(G_{x}\). Per ogni \(g \in G\) ci sono quindi esattamente \(|G_{x}|\) elementi \(h\) del gruppo per i quali risulta \(h \cdot x=g \cdot x\).
Il numero degli elementi distinti dell’orbita di \(x\) è quindi uguale al numero delle classi laterali sinistre dello stabilizzatore \(G_{x}\). Il teorema segue quindi dal teorema di Lagrange.
5) Le simmetrie
Il teorema di Burnside fornisce una formula per determinare le varie configurazioni (pattern) di un oggetto, che risultano distinte rispetto ad un gruppo di simmetrie.
È opportuno chiarire il significato di simmetria. In genere, una simmetria di un oggetto si riferisce ad una proprietà che rimane invariata rispetto ad un insieme di trasformazioni applicate all’oggetto. Il concetto di simmetria è presente in molte branche della matematica e anche in altre scienze. Ad esempio si può applicare a molte equazioni della matematica e della fisica, come le equazioni di Maxwell relative all’elettromagnetismo, i principi di conservazione della fisica, ecc.
In questo articolo ci interessa in particolare studiare la simmetria delle figure geometriche. Definiamo quindi i concetti di simmetria e isometria.
Definizione 5.1
In termini semplici, un’isometria è una trasformazione di una figura geometrica che preserva le distanze fra i punti della figura. La forma e le dimensioni dell’oggetto non variano.
Nel piano esistono solo \(4\) tipi di isometrie: traslazione, riflessione, rotazione e glisso-riflessione.
Si chiama glisso-riflessione lo spostamento composto da una riflessione e da una traslazione, definita da un vettore parallelo all’asse della riflessione.
Queste trasformazioni si chiamano anche moti rigidi. Notiamo che le isometrie sono casi particolari di permutazioni.
Definizione 5.2
Una simmetria su un oggetto è una trasformazione che agisce sull’oggetto, lasciandone inalterato l’aspetto. Alla fine della trasformazione o del movimento l’oggetto è uguale allo stato iniziale.
Le simmetrie di un oggetto sono associate alle isometrie. Quindi parliamo di simmetria di rotazione, di traslazione, ecc.
Ogni oggetto ha almeno una simmetria banale, chiamata identità, associata alla trasformazione nulla.
Il gruppo simmetrico di un oggetto è il gruppo delle isometrie, con l’operazione di composizione, che lasciano invariato l’oggetto.
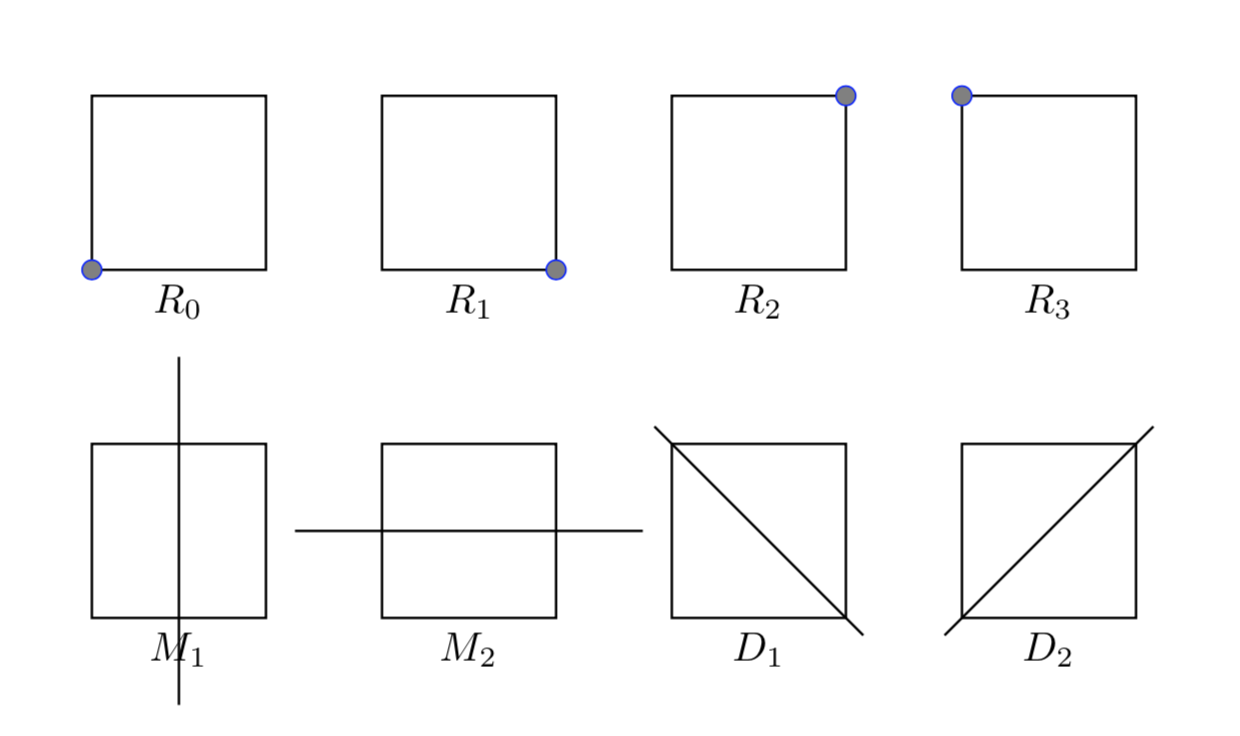
Esempio 5.1 – Le simmetrie del quadrato
Le isometrie che lasciano invariato un quadrato nel piano sono le \(4\) rotazioni in senso antiorario di angoli \(\left\{0, \dfrac{\pi}{2},\pi,\dfrac{3\pi}{2}\right\}\) e le \(4\) riflessioni rispetto alle due diagonali e alle due rette orizzontali e verticali, passanti per il centro del quadrato. Le \(8\) simmetrie sono illustrate nella figura sottostante:
L’insieme delle \(8\) simmetrie del quadrato forma un gruppo rispetto alla operazione di composizione di due simmetrie. La tabella di Cayley del gruppo delle simmetrie del quadrato è la seguente:
\[ \begin{array}{r|rrrrrrrr} – & R_0\ &\ R_1\ &\ R_2\ & \ R_3\ &\ M_1\ &\ M_2\ &D_1\ & D_2\\ \hline R_0 & R_0\ &\ R_1\ &\ R_2\ & \ R_3\ &\ M_1\ &\ M_2\ &D_1\ &D_2\\ \hline R_1 & R_1\ &\ R_2\ &\ R_3\ & \ R_0\ &\ D_2\ &\ D_1\ &M_1\ &M_2\\ \hline R_2 & R_2\ &\ R_3\ &\ R_0\ & \ R_1\ &\ M_2\ &\ M_1\ &D_2\ &D_1\\ \hline R_3 & R_3\ &\ R_0\ &\ R_1\ & \ R_2\ &\ D_1\ &\ D_2\ &M_2\ &M_1\\ \hline M_1 & M_1\ &\ D_1\ &\ M_2\ & \ D_2\ &\ R_0\ &\ R_2\ &R_1\ &R_3\\ \hline M_2 & M_2\ &\ D_2\ &\ M_1\ & \ D_1\ &\ R_2\ &\ R_0\ &R_3\ &R_1\\ \hline D_1 & D_1\ &\ M_2\ &\ D_2\ & \ M_1\ &\ R_3\ &\ R_1\ &R_0\ &R_2\\ \hline D_2 & D_2\ &\ M_1\ &\ D_1\ & \ M_2\ &\ R_1\ &\ R_3\ &R_2\ &R_0\\ \hline \end{array} \]Esercizio 5.2
Dimostrare che un poligono regolare di \(n\) lati ha \(2n\) simmetrie.
Esempio 5.3
Dimostrare che il cubo ha 48 simmetrie.
Per un approfondimento del concetto di simmetria e delle sue applicazioni vedere [2] e [5].
6) Il teorema di Burnside
A questo punto possiamo dimostrare il teorema di Burnside, che come già detto nell’introduzione era stato già stato formulato da Frobenius e Cauchy.
Teorema 6.1 – Teorema di Burnside
Sia G un gruppo di permutazioni che agisce su un insieme finito \(X\). Indichiamo con \( X / G\) l’insieme delle orbite distinte. Allora
Dimostrazione
La dimensione dell’orbita di \(x\) è \(|\text{Orb}(x)|\), quindi ognuno degli elementi dell’orbita di \(x\) contribuisce con \(\dfrac{1}{|\text{Orb}(x)|}\). Il numero totale delle orbite è
In base al teorema orbita-stabilizzatore e all’esercizio 4.5 abbiamo
\[ |X/G|= \sum\limits_{x \in X}\frac{1}{|\text{Orb}(x)|}=\sum\limits_{x \in X}\frac{G_{x}}{|G|}=\frac{1}{|G|}\sum\limits_{g \in G} |X_{g}| \]7) Applicazioni
7.1) Il conteggio delle colorazioni distinte
Sia \(N=\{1,2,\cdots, n\}\) e sia \(C\) un insieme finito di colori. Indichiamo con \(X\) l’insieme di tutte le possibili colorazioni di \(N\), cioè di tutte le funzioni
\[ f: N \to C \]Sia \(G\) un sottogruppo del gruppo simmetrico \(S_{n}\). Due colorazioni \(c_{1},c_{2}\) si dicono equivalenti se esiste una permutazione \(\pi \in G\) tale che \( \pi \cdot c_{1}=c_{2}\). Si tratta ovviamente di una relazione di equivalenza, e le diverse colorazioni corrispondo alle orbite. Il problema è determinare il numero delle colorazioni diverse.
Ogni permutazione di \(G\) agisce anche sull’insieme \(X\) delle colorazioni. Ad esempio supponiamo che \(n=4\) e \(r=2\), cioè \(N=\{1,2,3,4\}\) e \(C=\{B,R\}\), dove i simboli \(B,R\) indicano i colori bianco e rosso. La permutazione \(\sigma =(12)(34)\) agisce sull’insieme delle colorazioni e produce altre colorazioni. Ad esempio
Esempio 7.1 – Triangolo equilatero
Sia dato un triangolo equilatero. Ogni vertice può essere colorato con uno tra \(m\) colori. Sia \(G\) il gruppo delle rotazioni antiorarie di angoli \(\left\{0, \dfrac{2\pi}{3},\dfrac{4\pi}{3}\right\}\). Indichiamo con \(\sigma\) la rotazione antioraria di angolo \(\dfrac{2\pi}{3}\). Il gruppo delle simmetrie è quindi \(G=\{\sigma^{0}, \sigma,\sigma^{2}\}\).
Ricordiamo che la rotazione di zero gradi corrisponde alla permutazione identità \(\epsilon\).
Per calcolare il numero delle colorazioni distinte dobbiamo determinare le cardinalità degli insiemi di punti fissi \(X_{\sigma^{0}},X_{\sigma},X_{\sigma^{2}}\).
Chiaramente \(|X_{\sigma^{0}}|=m^{3}\), in quanto ogni colorazione è invariante con la permutazione identità. Per la rotazione \(\sigma\) la colorazione è invariante solo se i colori sono tutti uguali. Quindi \(|X_{\sigma}|=m\). Lo stesso vale per la rotazione \(\sigma^{2}\).
Quindi, applicando il teorema di Burnside, il numero \(k\) delle colorazioni distinte è
Esercizio 7.1
Risolvere l’esempio precedente considerando tutte le simmetrie del gruppo diedrale \(D_{3}\), contenente le \(3\) rotazioni e le \(3\) riflessioni rispetto agli assi di simmetria del triangolo equilatero.
Risposta: \(\left[ k= \dfrac{1}{6}(m^{3}+3m^{2}+2m)\right]\)
Esercizio 7.2
Determinare il numero delle distinte colorazioni dei vertici di un quadrato, con \(n\) colori. Sono ammesse le quattro rotazioni di angoli \(\left\{0,\dfrac{\pi}{2},\pi,\dfrac{3\pi}{2}\right\}\).
Risposta: \(\left[\dfrac{1}{4}(n^{4}+n^{2}+2n)\right]\)
Esercizio 7.3
Determinare il numero delle distinte colorazioni dei vertici di un rombo non quadrato, con \(n\) colori. Sono ammesse le due rotazioni (identità e rotazione di \(\pi\) intorno al centro) e le due riflessioni lungo le due diagonali.
Risposta: \(\left[\dfrac{1}{4}n^{2}(n+1)^{2}\right]\)
Esercizio 7.4 – Colorazioni di una scacchiera 4 x 4
Data una scacchiera \(4 \times 4\), determinare il numero delle distinte colorazioni con due colori \(R,N\), rispetto alle \(4\) rotazioni antiorarie del quadrato.
Soluzione
Il gruppo \(G\) delle simmetrie è costituito dalla \(4\) rotazioni del quadrato, con angoli di \(\left\{0,\dfrac{\pi}{2},\pi,\dfrac{3}{2}\pi\right\}\). Quindi \(G=\{\sigma^{0},\sigma,\sigma^{2},\sigma^{3}\}\), dove \(\sigma\) è la rotazione antioraria di \(90\) gradi. L’insieme \(X\) delle colorazioni contiene \(2^{16}=65536\) elementi. Per applicare il teorema di Burnside dobbiamo determinare le cardinalità degli insiemi di punti fissi relativi alle \(4\) permutazioni.
Per la permutazione identità abbiamo \(|X_{\sigma^{0}}|=2^{16}\).
Per calcolare \(X_{\sigma^{1}}\) osserviamo il seguente diagramma
dove gli elementi \(A,B,C,K\) appartengono all’insieme dei colori \(\{R,N\}\). Come si vede abbiamo \(4\) scelte indipendenti possibili, quindi \(|X_{\sigma^{1}}|=2^{4}\).
Procedendo in modo analogo si trova che \(|X_{\sigma^{2}}|=2^{8}\) e \(|X_{\sigma^{3}}|=|X_{\sigma^{1}}|\).
Mettendo insieme, abbiamo che il numero delle colorazioni distinte è
7.2) Il piccolo teorema di Fermat
Il piccolo teorema di Fermat afferma che, se \(p\) è un numero primo e \(m\) un intero, allora
\[ m^{p} \equiv m \pmod{p} \]Una formulazione equivalente è la seguente: se \(p\) è un numero primo e \(m\) è un intero non divisibile da \(p\), allora
\[ m^{p-1} \equiv 1 \pmod{p} \]Dimostriamo ora il piccolo teorema di Fermat mediante il teorema di Burnside.
Indichiamo con \(G\) il gruppo ciclico generato dalla permutazione \(\sigma=(1,2,..,p)\), dove \(p\) è un numero primo. Il gruppo contiene \(p\) elementi: \(\{\sigma^{0},\sigma, \cdots,\sigma^{2},\sigma^{p-1}\}\). Queste permutazioni possono essere interpretate anche come rotazioni dei vertici di un poligono regolare di \(p\) lati.
Supponiamo ora di avere \(m\) colori. Per ogni permutazione dobbiamo calcolare l’insieme dei punti fissi. Per la permutazione identità \(\sigma^{0}\) il numero delle colorazioni invarianti è chiaramente \(m^{p}\). Per ognuna delle altre \(p-1\) permutazioni solo le colorazioni con un solo colore rimangono invariate, poiché \(p\) è un numero primo, e quindi sono \((p-1) m\). In definitiva, per il teorema di Burnside, il numero delle colorazioni distinte \(k\) è:
Il numero delle colorazioni distinte \(k\) deve essere un intero positivo. Quindi \(m^p + (p-1)m\) deve essere divisibile per \(p\). Semplificando abbiamo:
\[ m^p+(p-1)m \equiv 0 \pmod{p} \Rightarrow m^p-m\equiv 0 \pmod{p} \]e il teorema di Fermat è dimostrato.
7.3) Altre applicazioni
Il concetto di simmetria è presente in molti fenomeni naturali e anche nei prodotti artificiali creati dall’uomo. È quindi naturale che il teorema di Burnside trovi applicazione in molti settori: matematica, fisica, chimica, musica, giochi, ecc.
Un esempio interessante il seguente: contare in quanti modi distinti possono essere posizionate \(n\) torri non attaccanti, su una scacchiera \(n \times n\). Il gruppo di simmetria da considerare è il gruppo diedrale \(D_{4}\), consistente di \(4\) rotazioni e \(4\) riflessioni. Per la soluzione vedere ad esempio il testo di Aigner [4].
Nella teoria musicale il teorema di Burnside può essere usato per enumerare gli acconti della scala temperata.
Per i dettagli vedere ad esempio [6].
Infine, trova applicazione anche in chimica, ad esempio per contare il numero di isomeri di una molecola organica. Come è noto gli isomeri sono molecole che hanno la stessa formula chimica, ma una diversa configurazione strutturale dei loro atomi.
Conclusione
Il teorema di Burnside è uno strumento molto efficace per contare le configurazioni distinte di un insieme di oggetti, in relazione ad un gruppo di simmetrie. Tranne in casi molto semplici, il numero delle possibili configurazioni è elevato e sarebbe estremamente complicato tentare di risolvere questi tipi di problemi, tentando di confrontarle tutte fra loro. Questo teorema è un esempio di come una teoria matematica astratta, come la teoria dei gruppi, possa fornire strumenti per risolvere problemi molto concreti.
In un prossimo articolo studieremo il teorema di enumerazione di Polya-Redfield, che generalizza il teorema di Burnside, fornendo ulteriori informazioni sulle proprietà delle configurazioni.
Bibliografia
[1]B. Baumslag, B. Chandler – Schaum’s Outline of Group Theory (McGraw-Hill)
[2]Roy McWeeny – Symmetry: An Introduction to Group Theory and its Applications (Dover)
[3]A. Tucker – Applied Combinatorics (Wiley)
[4]M. Aigner – A Course in Enumeration (Springer)
[5]H. Weyl – Symmetry (Princeton U.P.)
[6]D. Benson – Music: A Mathematical Offering (Cambridge U.P.)


0 commenti