Nell’articolo precedente abbiamo illustrato due risultati importanti sulla distribuzione dei numeri primi:
\[ \begin{array}{l} \displaystyle\lim_{x \to \infty}\pi(x)=\infty \\ \sum\limits_{p}{}\dfrac{1}{p}=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}+ \cdots=\infty \end{array} \]dove \(\pi(x)\) è la funzione che conta il numero dei primi che non superano \(x\). Il primo risultato è già presente negli ‘Elementi’ di Euclide, mentre il secondo è stato dimostrato da Eulero nel \(1737\), grazie alla sua formula prodotto, che ha introdotto per la prima volta la funzione zeta:
\[ \zeta(s) =\sum\limits_{n=1}^{\infty}\frac{1}{n^{s}}=\prod\limits_{p}^{}\frac{1}{\left(1- p^{-s}\right)} \quad s \gt 1 \]Rimaneva il problema di determinare una funzione che permettesse di calcolare il valore della \(\pi(x)\) per ogni valore di \(x\), oppure almeno che approssimasse il comportamento asintotico della \(\pi(x)\), al tendere di \(x\) all’infinito.
In questo articolo studieremo alcuni risultati di Eulero e le congetture di Legendre e Gauss, che rappresentano dei passi importanti verso la dimostrazione del teorema dei numeri primi, che avverrà nel \(1896\) da parte dei matematici Hadamard e de la Vallée Poussin:
dove il simbolo di Landau \(\sim\) significa che risulta
\[ \lim_{x\to\infty}\frac{\pi(x)}{x/\log x}=1 \]1) La serie armonica e il logaritmo naturale
Le proprietà del logaritmo naturale e della serie armonica sono strettamente correlate alla distribuzione dei numeri primi. La serie armonica è così definita:
\[ \sum\limits_{k=1}^{\infty}\frac{1}{k}=1+\frac{1}{2}+ \frac{1}{3}+\frac{1}{4}+ \cdots \]Come è noto ogni serie del tipo \(\sum\limits_{k=1}^{\infty}\dfrac{1}{k^{\alpha}}\), con \(\alpha \gt 1\), converge ad un valore finito. A prima vista si potrebbe pensare che anche la serie armonica converge. Tuttavia Nicole Oresme (ca. 1325-1382) dimostrò per primo che la serie è divergente.
Teorema 1.1
La serie armonica è divergente.
Dimostrazione
Riportiamo la classica dimostrazione di Oresme. Indicata con \(S\) la somma della serie abbiamo:
L’ultima serie è chiaramente divergente.
Si possono dare molte altre dimostrazioni della divergenza della serie armonica. Riproponiamo la pseudo-dimostrazione di Eulero, che parte dallo sviluppo in serie della funzione logaritmo:
Questo sviluppo è valido solo se \(-1 \le x \lt 1\). Tuttavia Eulero assume \(x=1\) ottenendo:
\[ \ln (1-1)= -\infty = -\left(1 + \frac{1}{2} + \frac{1}{3} +\frac{1}{4} + \cdots\right) \]Esercizio 1.1
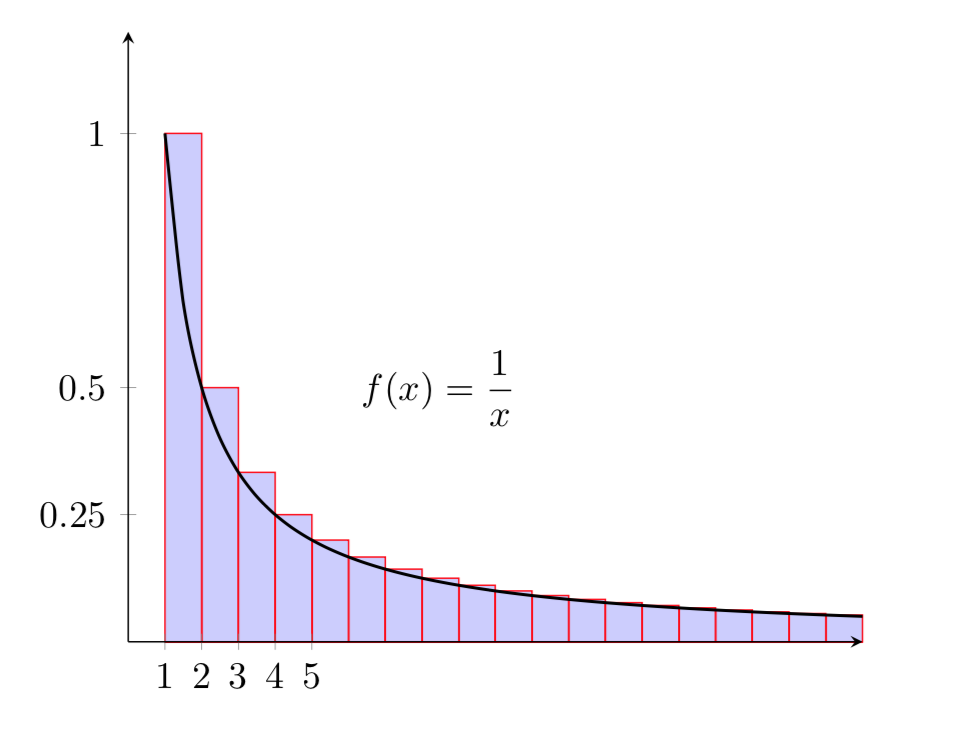
Dimostrare che a serie armonica è divergente tramite il criterio integrale, calcolando l’integrale \(\int\limits_{1}^{\infty}\dfrac{dx}{x}\).
Suggerimento
Ricordiamo che l’integrale di Riemann può essere definito come l’estremo inferiore delle somme integrali superiori, come illustrato nella figura seguente. Per ogni decomposizione dell’asse delle \(x\) si sommano le aree dei rettangoli. Per ogni rettangolo l’altezza coincide con l’estremo superiore che la funzione assume nella base.
Definizione 1.1 – La somma armonica
La somma armonica di ordine \(n\), indicata con \(H_{n}\), è la somma parziale della serie armonica:
Il numero \(H_{n}\) viene anche chiamato numero armonico. La somma armonica verifica la seguente equazione ricorsiva:
\[ H_{n}=H_{n-1}+ \frac{1}{n} \]Esercizio 1.2
Dimostrare che la funzione generatrice della successione \(a_{n}=\dfrac{1}{n}\) è la funzione \(\ln \dfrac{1}{1-x}\).
Ricordiamo che la funzione generatrice di una successione \(a_{n}\) è una funzione \(f(x)\) il cui sviluppo in serie è \(f(x)=\sum\limits_{n=0}^{\infty}a_{n}x^{n}\).
Esercizio 1.3
Dimostrare che la funzione generatrice della successione \(H_{n}\) è la funzione
Teorema 1.2
Il numero \(H_{n}\) non è mai un intero positivo per \(n \gt 1\).
Dimostrazione
Poniamo
Se \(x\) fosse un intero avremmo \(x \ge 1\) e inoltre \(k \gt 1\), cioè \(k \ge 2\). Indichiamo con \(p\) il più grande numero primo \(p \le k+2\). Per il postulato di Bertrand (vedi articolo) esiste un numero primo \(q\) compreso fra \(p\) e \( 2p\). Inoltre risulta \(2p \gt k+2\). Infatti se fosse \(2p \le k+2\) si avrebbe \(p \lt q \lt k+2\), contrariamente all’ipotesi su \(p\).
Quindi abbiamo
Da questo segue che fra gli elementi della somma \(\dfrac{1}{2}+ \dfrac{1}{3}+ \cdots + \dfrac{1}{k+2}\) solo uno ha il denominatore divisibile per \(p\). Riducendo al minimo comune denominatore abbiamo che tutti i numeratori tranne uno risultano divisibili per \(p\). D’altra parte \(p\) divide anche il denominatore comune e quindi la somma non può essere un intero.
I numeri armonici sono numeri razionali. Come è noto un numero razionale può avere una rappresentazione decimale finita, oppure illimitata periodica.
I valori dei primi numeri armonici sono:
Come si vede i numeri \(H_{1},H_{2},H_{6}\) hanno una rappresentazione decimale finita, mentre \(H_{3},H_{4},H_{5}\) hanno una rappresentazione decimale illimitata periodica. Vale il seguente teorema:
Teorema 1.3
I numeri razionali \(H_{n}\) sono tutti decimali illimitati periodici, ad eccezione dei seguenti tre casi:
Per una dimostrazione vedere [7].
Esercizio 1.4
Dimostrare che i numeri armonici possono essere rappresentati mediante l’integrale
1.1) Il comportamento asintotico della serie armonica
Poiché la funzione \(f(x)=\dfrac{1}{x}\) è decrescente nell’intervallo \([1,n]\) si ha
\[ \frac{1}{2}+ \frac{1}{3}+ \cdots + \frac{1}{n} \lt \int\limits_{1}^{n}\frac{1}{x}dx=\ln n \lt 1+ \frac{1}{2}+ \frac{1}{3}+ \cdots \frac{1}{n-1} \]e quindi
\[ \ln n + \frac{1}{n} \lt H_{n} \lt \ln n +1 \] \[ \frac{1}{n} \lt H_{n} – \ln n \lt 1 \]Quindi la differenza \(S_{n}=H_{n}-\ln n\) è una successione limitata nell’intervallo \([0,1]\). Resta da dimostrare che il limite esiste e quindi calcolarne il valore.
Teorema 1.4
La successione \(S_{n}\) è convergente. Quindi esiste il limite
Dimostrazione
Sappiamo già che \(S_{n}=H_{n}- \ln{n}\) è una successione limitata. Dimostriamo che è anche una successione monotona decrescente. Per questo calcoliamo
Se integriamo la disuguaglianza \(\dfrac{1}{n+1} \le \dfrac{1}{x} \le \dfrac{1}{n}\) nell’intervallo \([n,n+1]\) otteniamo
\[ \frac{1}{n+1} \le \ln\frac{n+1}{n} \le \frac{1}{n} \]e quindi
\[ \frac{1}{n+1}- \frac{1}{n} \le \frac{1}{n+1}- \ln\frac{n+1}{n}=S_{n+1}-S_{n} \le 0 \]Quindi \(S_{n}\) è una successione monotona decrescente e limitata, e dall’Analisi Matematica sappiamo che questo comporta che è una successione convergente ad un limite finito.
Il limite della successione \(S(n)\) è compreso nell’intervallo \([0,1]\). Questo numero viene indicato con il simbolo \(\gamma\) ed è chiamato costante di Eulero-Mascheroni. Un valore approssimato della costante \(\gamma\) già calcolato da Eulero è
\[ \gamma = 0,577215664901532 \]Ad oggi non si è riusciti a dimostrare se \(\gamma\) è un numero razionale o irrazionale. Papanikolaou nel \(1997\) ha calcolato la frazione continua di \(\gamma\), dimostrando che se \(\gamma\) è un numero razionale \(\dfrac{a}{b}\) allora il denominatore \(b\) deve avere almeno \(242080\) cifre decimali.
Definiamo ora i numeri \(H_{n,k}= \sum\limits_{m=1}^{n}\dfrac{1}{m^{k}}\). Osserviamo che
\[ \lim_{n \to \infty}H_{n,k}=\zeta(k) \]dove \(\zeta(k)\) è la funzione zeta di Riemann.
Esercizio 1.5 – Eulero
Dimostrare che
La serie è alternante con numeri decrescenti e converge condizionatamente.
Suggerimento
Ricordare lo sviluppo di Taylor della funzione logaritmo
e calcolare i valori nei punti \(x=\dfrac{1}{k},k=1,2,\cdots\). Sommando i primi \(n\) termini si ottiene
\[ \ln(n+1) = H_{n}-\frac{H_{n,2}}{2}+\frac{H_{n,3}}{3}- \]1.2) La funzione gamma
La funzione gamma è stata introdotta da Eulero come generalizzazione del fattoriale a valori non interi. È una funzione speciale che appare in molte aree della matematica e della fisica matematica. In particolare è strettamente collegata con la funzione zeta di Riemann.
Si possono dare diverse definizioni equivalenti. La seguente è la definizione come integrale dipendente da un parametro reale:
Per ogni valore della variabile \(x\) il valore della funzione gamma è ottenuto calcolando l’integrale definito. L’integrale è convergente per \(x \gt 0\).
Esercizio 1.6
Dimostrare che \(\Gamma(1)=1\).
Teorema 1.5 – Formula di ricorrenza
\[ \Gamma(x+1)=x \Gamma (x) \]Per la dimostrazione effettuare l’integrazione per parti.
Mediante il teorema precedente è possibile estendere la funzione gamma anche a valori reali negativi. Infatti possiamo scrivere l’equazione funzionale in questo modo
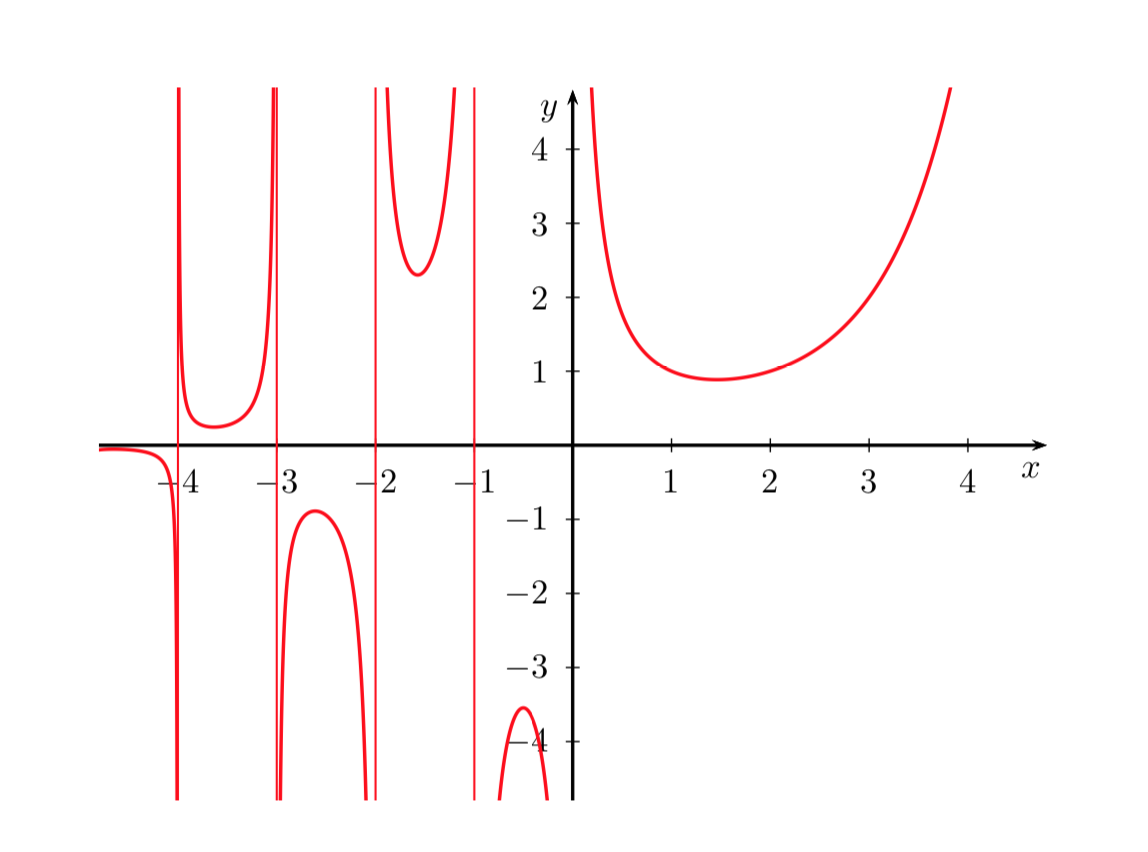
\[ \Gamma(x) = \frac{\Gamma(x+1)}{x} \quad -1 \lt x \lt 0 \]Ripetendo questo procedimento possiamo definire la funzione gamma su tutto l’asse reale negativo, ad esclusione degli interi non positivi \((0,-1,-2,\cdots)\).
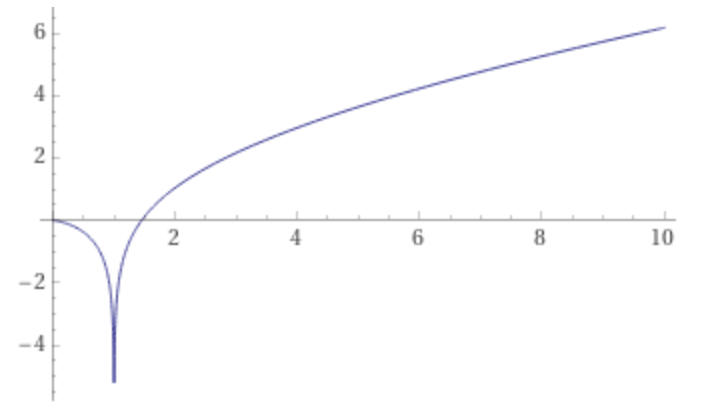
Come si vede dai grafici la funzione gamma non ha zeri sull’asse reale e ha dei punti di discontinuità negli interi non positivi, dove assume valori infiniti.
Dal teorema precedente, se \(x\) è un intero positivo abbiamo
Esercizio 1.7
Dimostrare che \(\Gamma(\frac{1}{2})=\sqrt{\pi}\).
Per la dimostrazione utilizzare il famoso integrale di Gauss
\[ \int\limits_{-\infty}^{+\infty}e^{-x^{2}}dx=\sqrt{\pi} \]La funzione gamma ha diverse rappresentazioni, tra loro equivalenti. Mediante il teorema di fattorizzazione di Weierstrass dell’analisi complessa si può dimostrare il seguente
Teorema 1.6
\[ \frac{1}{\Gamma(x)}=xe^{\gamma x}\prod\limits_{n=1}^{\infty}(1+\frac{s}{n})e^{-\frac{x}{n}} \]Esercizio 1.8
Dimostrare che
Suggerimento
Derivare il logaritmo del teorema precedente.
Esercizio 1.9
Dimostrare che una definizione equivalente della costante di Eulero-mascheroni è la seguente
2) Eulero e la serie dei numeri primi
Eulero può essere considerato il padre della Teoria Analitica dei Numeri. La formula prodotto di Eulero per la prima volta ha stabilito una connessione fra la distribuzione dei numeri primi e la funzione zeta di Riemann. Eulero non si è limitato a dimostrare che la serie dei reciproci dei primi è divergente, ma ha scoperto anche il comportamento asintotico della serie.
2.1) La serie dei reciproci dei numeri primi
Nel \(1737\) Eulero presentò una sua pubblicazione ‘Variae observationes circa series infinitas’ all’accademia di San Pietroburgo, nella quale tra i diversi teoremi era contenuto il seguente:
Teorema 2.1 – Eulero
La somma dei reciproci dei numeri primi
è infinitamente grande, ma è infinite volte minore della serie armonica
La somma della prima serie è il logaritmo della somma della seconda. Con la notazione moderna il teorema di Eulero è
\[ \sum\limits_{p \le x}\frac{1}{p} \approx \ln \ln x \]Dimostrazione
Riportiamo la pseudo-dimostrazione di Eulero, che parte dalla formula prodotto, per \(s=1\), dove in realtà la formula non è valida:
Ricordando lo sviluppo in serie del logaritmo, con \(x=\dfrac{1}{p}\) abbiamo
\[ \ln \left(1-\frac{1}{p}\right) = -\frac{1}{p} – \frac{1}{2p^{2}} – \frac{1}{3p^{3}} – \cdots \]Prendendo i logaritmi nella formula prodotto di Eulero abbiamo
\[ \ln \left(\sum\limits_{n=1}^{\infty}\frac{1}{n}\right)= \sum\limits_{p}^{}\frac{1}{p} + \sum\limits_{n=2}^{\infty} \sum\limits_{p}^{}\frac{1}{np^{n}} \]Dimostriamo ora che la doppia serie è convergente. Abbiamo
\[ \sum\limits_{n=2}^{\infty} \sum\limits_{p}^{}\frac{1}{np^{n}} \lt \sum\limits_{n=2}^{\infty} \sum\limits_{m=2}^{\infty}\frac{1}{nm^{n}} \lt \frac{1}{2} \sum\limits_{n=2}^{\infty} \sum\limits_{m=2}^{\infty}\frac{1}{m^{n}} \]L’ultima doppia serie è chiaramente convergente: basta invertire l’ordine e calcolare la serie geometrica.
Poiché la serie armonica cresce come la funzione logaritmo, il teorema di Eulero è dimostrato.
Naturalmente la dimostrazione di Eulero non rispetta il rigore necessario nel trattare le serie infinite.
Una dimostrazione rigorosa verrà data da Mertens nel \(1874\). Studieremo i teoremi di Mertens in un articolo successivo.
2.2) Derivazione euristica del teorema dei numeri primi
La formula di Eulero sull’ordine di grandezza della serie dei reciproci dei numeri primi introduce per la prima volta la funzione logaritmo, che ha un ruolo fondamentale nella determinazione della distribuzione dei numeri primi. Di fatto è un primo passo importante verso la dimostrazione del teorema dei numeri primi.
Disponiamo i numeri primi in ordine crescente:
Il teorema dei numeri primi \(\pi(x) \sim \dfrac{x}{\ln x}\) afferma sostanzialmente che per valori grandi di \(n\) l’ordine di grandezza di \(p_{n}\) è
\[ p_{n} \sim n \ln n \quad n \to \infty \]Ricordiamo che questo non significa che la differenza tende a zero, ma che il rapporto tende a \(1\). In modo equivalente si può affermare che la densità dei numeri primi è dell’ordine di \(\dfrac{1}{\ln n}\).
A partire dalla formula di Eulero
\[ F(x) = \sum\limits_{p \lt x}\frac{1}{p} \approx \ln \ln x \]si può arrivare al teorema dei numeri primi. La derivata della funzione \(F(x)\) è
\[ F'(x) \approx \dfrac{1}{x \ln x} \]Supponiamo di calcolare il nuovo valore \(F(x+1)\) a partire da \(F(x)\). Se \(x\) è un numero primo la funzione aumenta di \(\dfrac{1}{x}\) altrimenti rimane costante. Quindi la frequenza dei primi deve essere circa \(\dfrac{1}{\ln x}\).
Naturalmente non si tratta di una dimostrazione rigorosa. Tuttavia i risultati di Eulero costituiscono un contributo fondamentale verso il chiarimento del mistero della distribuzione dei numeri primi.
3) Legendre
Adrien-Marie Legendre (1752-1833) è stato un grande matematico francese, vissuto nel periodo della rivoluzione francese. Ha dato grandi contributi in molti settori: Analisi Matematica, Algebra, Teoria dei Numeri, Statistica. Tra le sue opere principali ricordiamo: ‘Eléments de Géométrie’, ‘Essai sur la théorie des nombres’, ‘Exercices de calcul intégral’, ‘Fonctions elliptiques’.
Nella sua opera relativa alla teoria dei numeri sono trattati vari argomenti, tra cui anche le proprietà dei numeri primi. In particolare Legendre fece una congettura che è molto vicina al teorema dei numeri primi. Egli effettuò molti calcoli sulla frequenza dei numeri primi e propose inizialmente la seguente formula:
dove \(A,B\) sono delle costanti. Si tratta di una formula basata su evidenze sperimentali.
In seguito diede la seguente versione più precisa, basata sulle tabulazioni dei numeri primi disponibili all’epoca:
dove \(A(x) \approx 1,08366\).
Il significato di questa formula non è del tutto chiaro. Probabilmente Legendre intendeva che \(\lim_{x \to \infty}A(x)=1,08366\).
Oggi possiamo utilizzare tabelle di primi molto più grandi di quelle che aveva a disposizione Legendre, e si trova che il valore migliore per \(A(x)\) è uguale a \(1\).
In seguito anche il matematico russo Chebyshev dimostrò che la congettura di Legendre non poteva essere vera, a meno che \(A(x)=1\).
Sviluppiamo in serie la funzione si Legendre:
\[ \frac{x}{\ln x – A}=\frac{x}{\ln x}[1+ \frac{A}{\ln x}+ \left(\frac{A}{\ln x}\right)^{2}+ \cdots] = \\ \frac{x}{\ln x}+ \frac{Ax}{(\ln x)^{2}} + R(x) \]dove \(R(x)\) è molto più piccolo dell’ultimo termine. Mediante questo sviluppo in serie si dimostra il seguente:
Teorema 3.1
Supposto vero il teorema dei numeri primi \(\pi(x)\sim \dfrac{x}{\ln x}\), allora
per qualunque valore di \(A\). Da questo punto di vista quindi la congettura di Legendre è equivalente al teorema dei numeri primi.
4) L’integrale logaritmico
Ricordiamo alcune proprietà dell’integrale logaritmico, che ha un ruolo essenziale nella congettura di Gauss. È definito mediante il seguente integrale:
\[ li(x) = \int\limits_{0}^{x}\frac{dt}{\ln t} \]La funzione integranda \(\dfrac{1}{\ln x}\) ha una singolarità nel punto \(x=1\). Tuttavia l’integrale ha senso come valore principale di Cauchy, cioè
\[ li(x) = \lim_{\epsilon \to 0+} \left(\int_{0}^{1-\epsilon}\frac{dt}{\ln t}+ \int_{1+\epsilon}^{x}\frac{dt}{\ln t}\right) \]Oltre alla definizione sopra riportata (chiamata anche “americana”) è molto utilizzata anche la seguente definizione (chiamata anche “europea” o integrale logaritmico Euleriano), il cui dominio è l’intervallo \([2,\infty)\):
\[ Li(x)=li(x)-li(2) = \int_{2}^{x}\frac{dt}{\ln t} \]Il valore dell’integrale nell’intervallo \([0,2]\) è \(li(2) \approx 1,045163\).
Ricordiamo che alcuni autori utilizzano i simboli \(li(x),Li(x)\) con significato opposto.
Esercizio 4.1
Dimostrare che il seguente integrale converge e calcolarne il valore:
Esercizio 4.2
Dimostrare la seguente formula:
Esercizio 4.3
Mediante integrazione per parti dimostrare la seguente formula:
Esercizio 4.4
Dividendo l’intervallo di integrazione \([2,x]\) in due intervalli \([2,\sqrt{x}]\) e \([\sqrt{x},x]\), dimostrare la seguente relazione
Esercizio 4.5
Generalizzare l’esercizio 4.3 integrando ripetutamente per parti.
dove \(C_{n}\) è indipendente da \(x\).
Si può dimostrare che l’errore, per un fissato valore di \(n\), cresce meno rapidamente dell’ultimo termine \(\dfrac{x}{(\ln x)^{n}}\), quando \(x \to \infty\). Infatti vale la seguente stima dell’errore:
\[ \int\limits_{2}^{x}\frac{dt}{(\ln t)^{n}}=O \left(\frac{x}{(\ln x)^{n}}\right) \]La notazione di Landau \(f(x)=O(g(x))\) per \(x \to \infty\) significa che, date due funzioni \(f(x),g(x)\), esiste una costante positiva \(K\) tale che al crescere di \(x\) si ha definitivamente \(\mid f(x) \mid \le K\mid g(x) \mid\).
La formula dell’esercizio precedente può essere messa nella seguente forma, utilizzano dil simbolo di Landau \(\sim\):
Oltre a dimostrare il teorema dei numeri primi nel \(1896\), de la Valleé Poussin dimostrò che una relazione analoga alla precedente vale per la funzione \(\pi(x)\):
\[ \pi(x) \sim \frac{x}{\ln x}+ \frac{x}{(\ln x)^{2}} +\frac{2x}{(\ln x)^{3}} + \frac{6x}{(\ln x)^{4}}+\cdots \\ + \frac{(n-1)!x}{(\ln x)^{n}} \]Fissato un intero positivo \(n\), l’errore dell’approssimazione è molto minore dell’ultimo termine. Prendendo \(n=1\) abbiamo il teorema dei numeri primi.
Se ci fermiamo a \(n=2\) possiamo dimostrare che nella congettura di Legendre il valore ottimale è \(A=1\). Ricordando lo sviluppo della funzione dl Legendre del paragrafo precedente e utilizzando la formula di de la Valleé Poussin con \(n=2\) abbiamo:
Da questa forma deriva
\[ Li(x) \sim \frac{x}{\ln x} +\frac{x}{(\ln x)^{2}} \]Confrontando con lo sviluppo in serie della funzione di Legendre \(\dfrac{x}{\ln x – A}\), possiamo dedurre che la scelta ottimale per l’approssimazione di Legendre è \(A=1\).
5) La congettura di Gauss
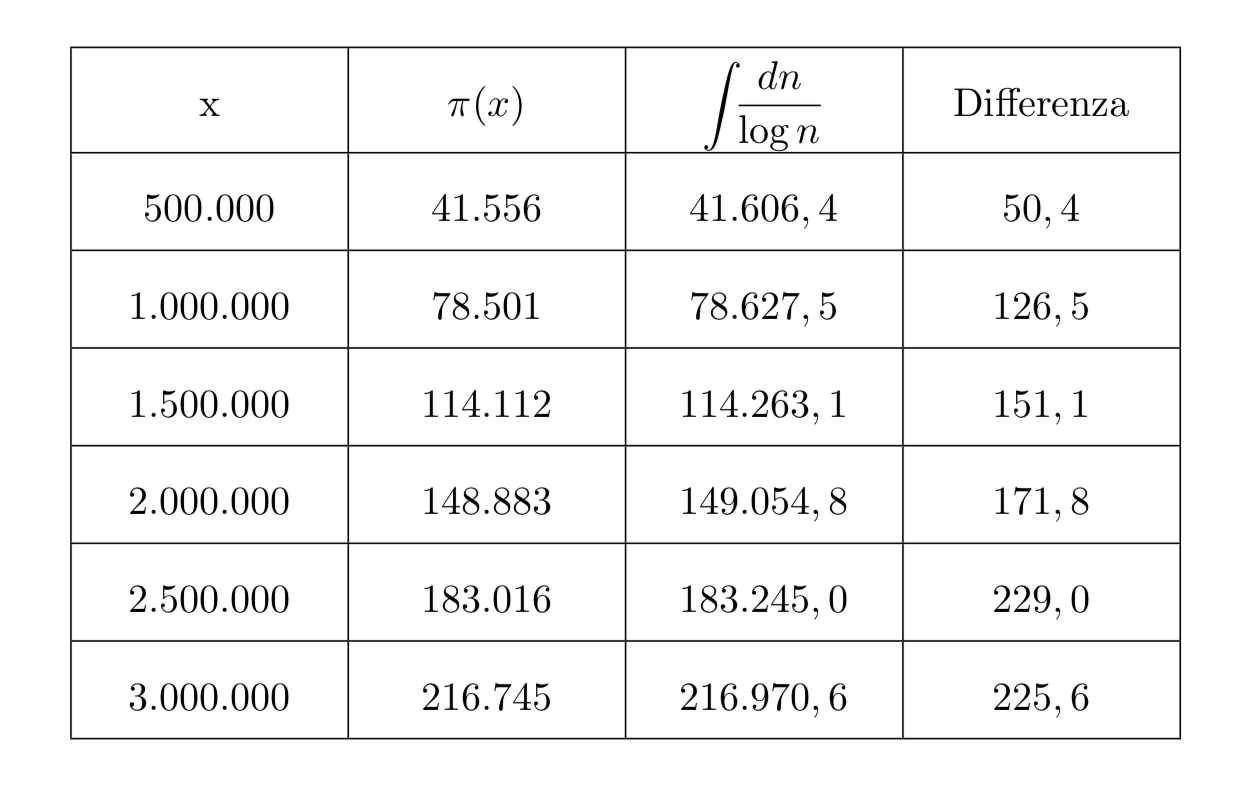
Gauss si occupò del problema della distribuzione dei primi fin dal \(1792\), anche se non pubblicò i suoi risultati. Dai suoi studi osservò che la densità dei numeri primi è mediamente dell’ordine di \(\dfrac{1}{\ln x}\). Il risultato di Gauss non è dovuto a considerazioni teoriche, ma è frutto soprattutto di osservazioni sperimentali sulle tabelle di primi disponibili all’epoca. Nel \(1849\) pubblicò la seguente tabella:
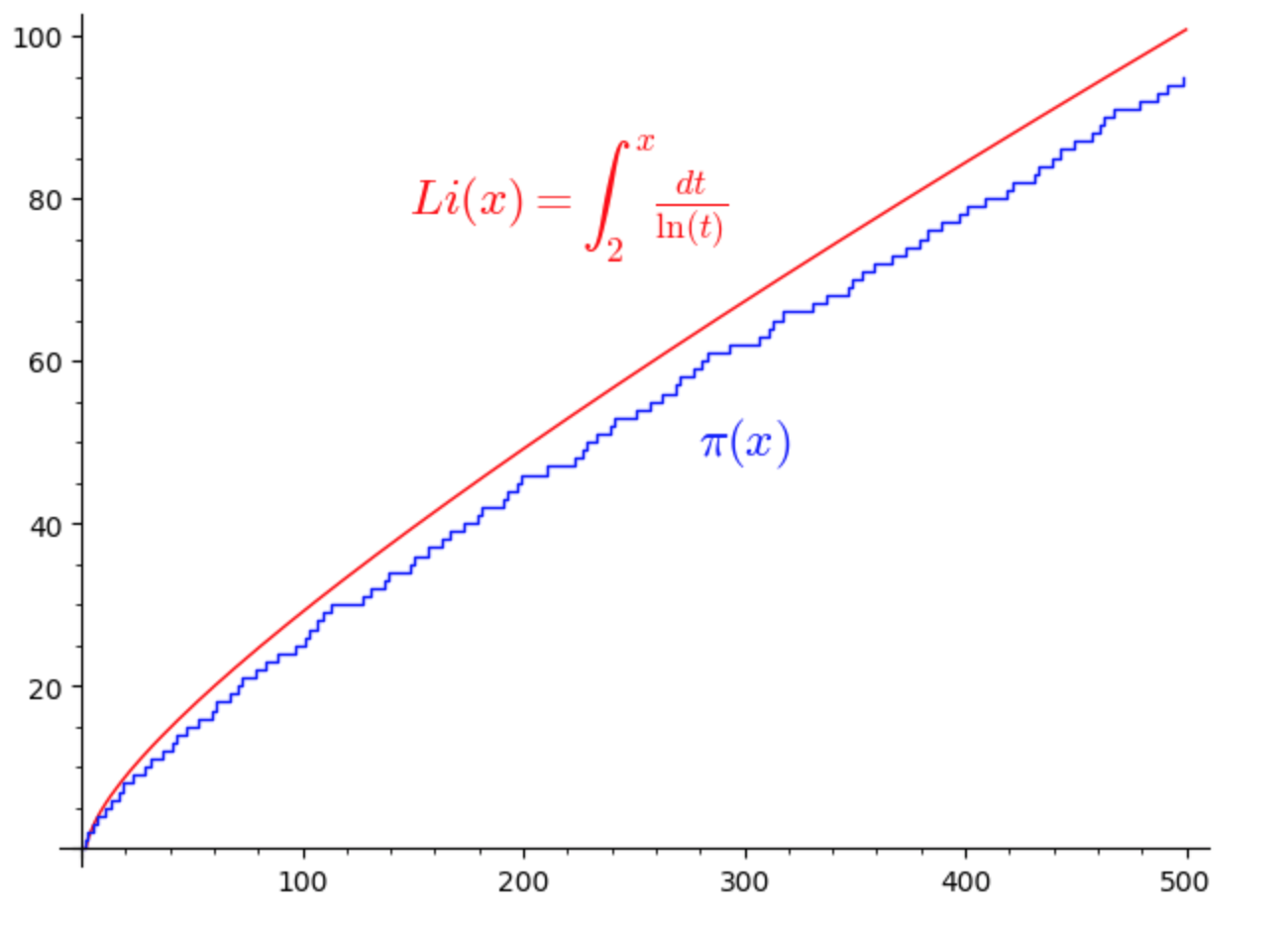
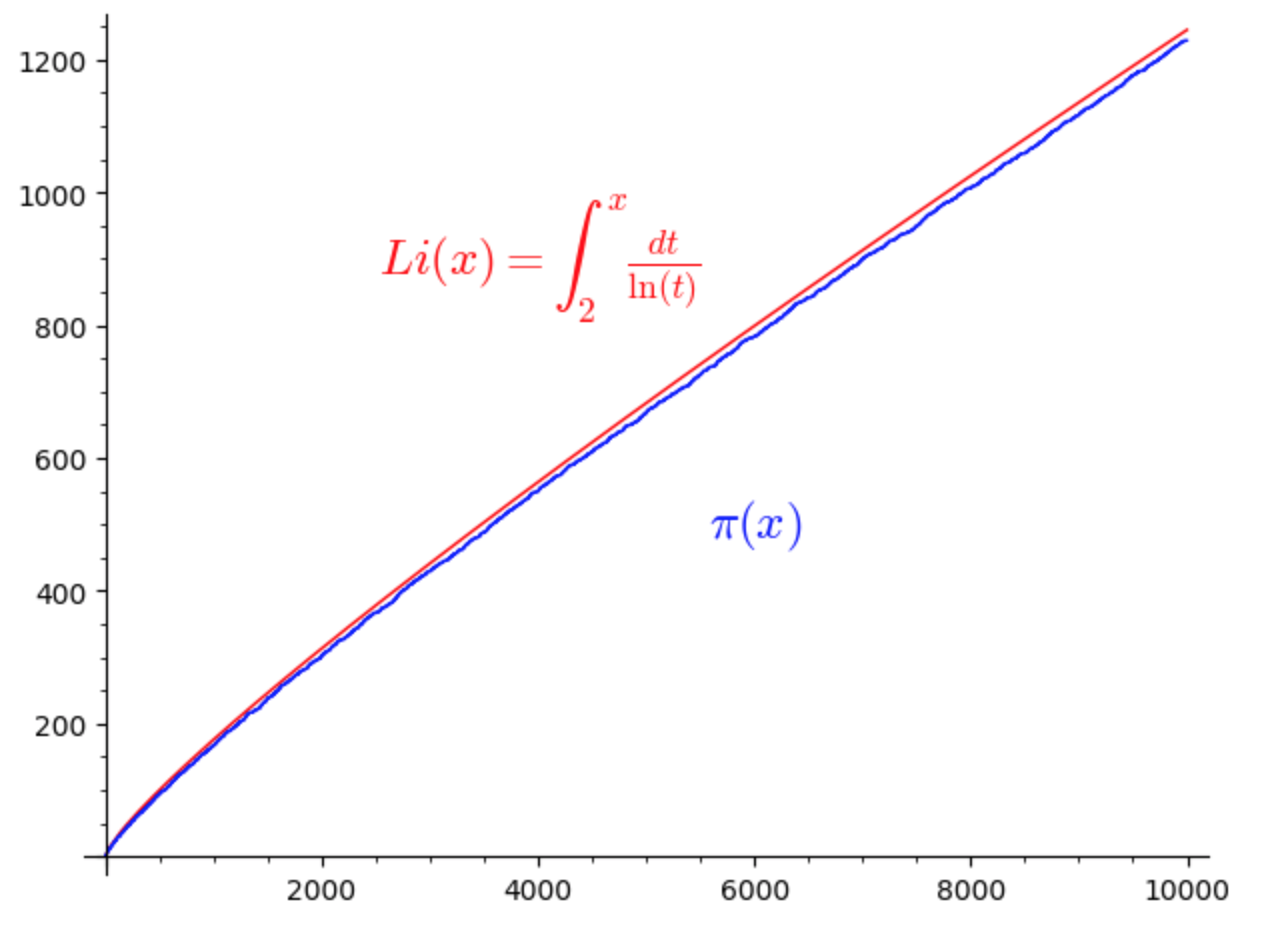
I due grafici seguenti illustrano l’andamento delle due curve al crescere di \(x\):
La congettura di Gauss può essere espressa in questo modo:
\[ \pi (x) \sim Li(x)= \int\limits_{2}^{x}\frac{dt}{\ln t} \]Teorema 5.1
La congettura di Gauss \(\pi (x) \sim Li(x)\) è equivalente al teorema dei numeri primi \(\pi(x) \sim \dfrac{x}{\ln x}\).
Dimostrazione
Ricordiamo la relazione dimostrata in precedenza:
Applicando la regola di de l’Hôpital per il calcolo dei limiti abbiamo:
\[ \lim_{x \to \infty}\dfrac{\int\limits_{2}^{x}\dfrac{dt}{(\ln t)^{2}}}{Li(x)} = \lim_{x \to \infty}\frac{\ln x}{(\ln x)^{2}} =0 \]Da questo deriva che \(Li(x) \sim \dfrac{x}{\ln x}\).
La seguente tabella confronta la formula di Gauss con quella di Legendre:
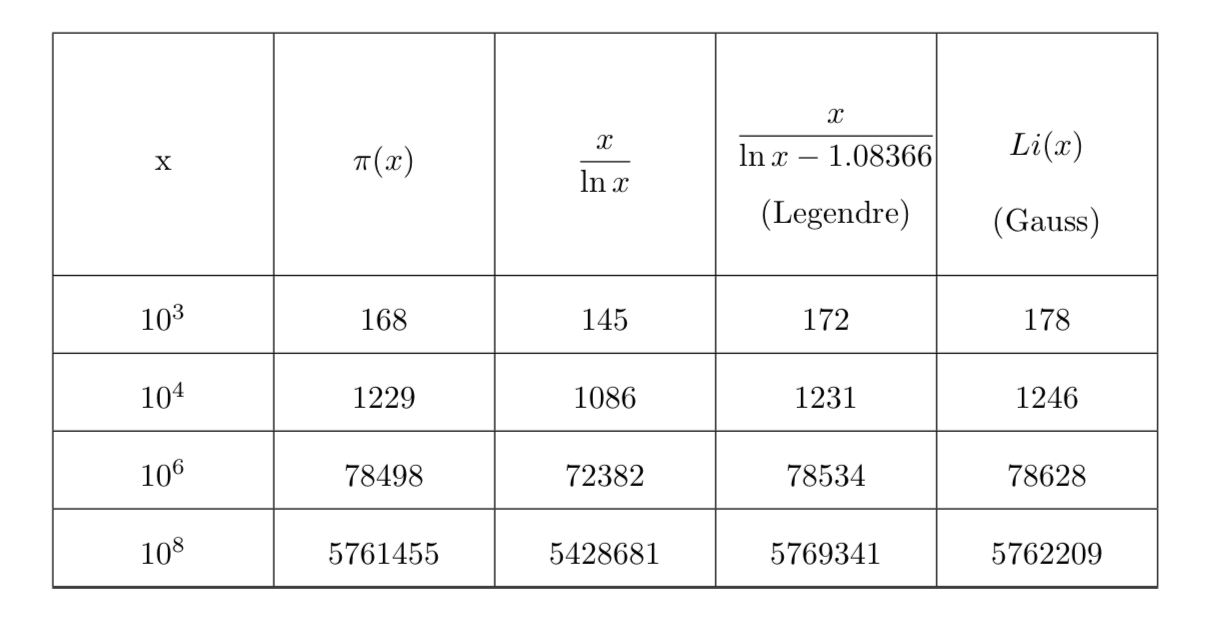
6) Teorema di Littlewood
Confrontando i valori delle tabelle si nota che il valore della funzione \(\pi(x)\) è sempre minore del valore di \(Li(x)\). Lo stesso Gauss notò che \(Li(x)\) era sempre maggiore di \(\pi(x)\) almeno fino al valore calcolato di \(x=3.000.000\).
Tuttavia Littlewood nel \(1914\) dimostrò che la differenza
cambia segno infinite volte al crescere di \(x\).
Precisamente Littlewood ha dimostrato che esistono delle costanti positive \(A,B\) tali che per infiniti valori di \(x\) valgono le seguenti disuguaglianze
Per una dimostrazione vedere il libro di Ingham [2].
Non si conosce il primo valore di \(x\) nel quale avviene il cambiamento di segno. Mediante considerazioni teoriche e calcoli complessi Bays e Hudson nel \(1999\) hanno dimostrato che il primo valore dovrebbe essere minore di \(10^{316}\). In particolare hanno dimostrato che ci sono almeno \(10^{153}\) valori interi di \(x\) nelle vicinanze di \(1,39822 \times 10^{316}\) per i quali \(\pi(x) \gt Li(x)\). Per la dimostrazione vedere [6].
Conclusione
Nonostante siano basate su osservazioni sperimentali delle tabelle dei primi, le congetture di Legendre e Gauss hanno rappresentato un passo fondamentale per la comprensione della distribuzione dei numeri primi. Nel prossimo articolo studieremo i risultati del matematico russo Chebyshev (1821-1894), i cui teoremi confermeranno le predizioni di Legendre e Gauss. Chebyshev può essere considerato il precursore del teorema dei numeri primi, anche se non è riuscito a darne una dimostrazione rigorosa nella sua forma completa, avvenuta solo nel \(1896\), due anni dopo la sua morte.
Bibliografia
[1]A. M. Legendre – Essai sur la theorie de Nombres (Cambridge U.P. 2009)
[2]A. E. Ingham – The Distribution of Prime Numbers (Cambridge M.L., 1992)
[3]W. Sierpinski – Elementary Theory of Numbers (North Holland)
[4]T. Apostol – Introduction to Analytic NumberTheory (Springer, 1976)
[5]R. Plymen – The Great Prime Number Race (AMS 2020)
[6]C. Bays, R. H. Hudson – A new bound for the smallest x with \(\pi(x) > Li(x)\) (Math. Comp. 69, 1999)
[7]J. Havil – Gamma: Exploring Euler’s Constant (Princeton U.P.)

0 commenti