Un numero primo è un numero naturale maggiore di \(1\) che ha come soli divisori il numero \(1\) e se stesso. La serie iniziale dei numeri primi è la seguente:
\[ 2,3,5,7,11,13,17,19,23, \cdots \]Nonostante la semplicità della definizione, il mondo dei numeri primi ha una complessità straordinaria, in gran parte ancora da scoprire.
I numeri primi sono i blocchi fondamentali con i quali è costruito l’universo di tutti i numeri. Inoltre nell’età moderna hanno assunto un ruolo essenziale per la sicurezza dei dati gestiti dai computer e delle comunicazioni sulle reti.
Alcuni dei problemi principali riguardanti i numeri primi sono i seguenti:
- determinare la frequenza dei numeri primi all’interno dell’insieme dei numeri naturali;
- trovare delle formule in grado di generare tutti i numeri primi;
- riconoscere se un numero intero è primo oppure composto;
- dato un numero composto, determinare i fattori primi che lo dividono.
Questo articolo è il primo di una serie in cui studieremo le proprietà dei numeri primi e della loro distribuzione asintotica, partendo dai risultati iniziali scoperti dagli antichi Greci fino al periodo attuale.
1) Il problema della distribuzione dei numeri primi
Lo studio della distribuzione dei numeri primi è una branca molto interessante e complessa della Teoria dei Numeri. Il problema fondamentale è lo studio delle proprietà della seguente funzione aritmetica \(\pi(x)\), che conta il numero dei primi minori od uguali a \(x\):
\[ \pi(x) = | \{p \in \mathbb{P}: p \le x \}| \quad x \gt 1 \]dove \( \mathbb{P}=\{2,3,5,7,11,13, \cdots \}\) è l’insieme dei numeri primi. I valori iniziali della funzione \(\pi(x)\) sono i seguenti:
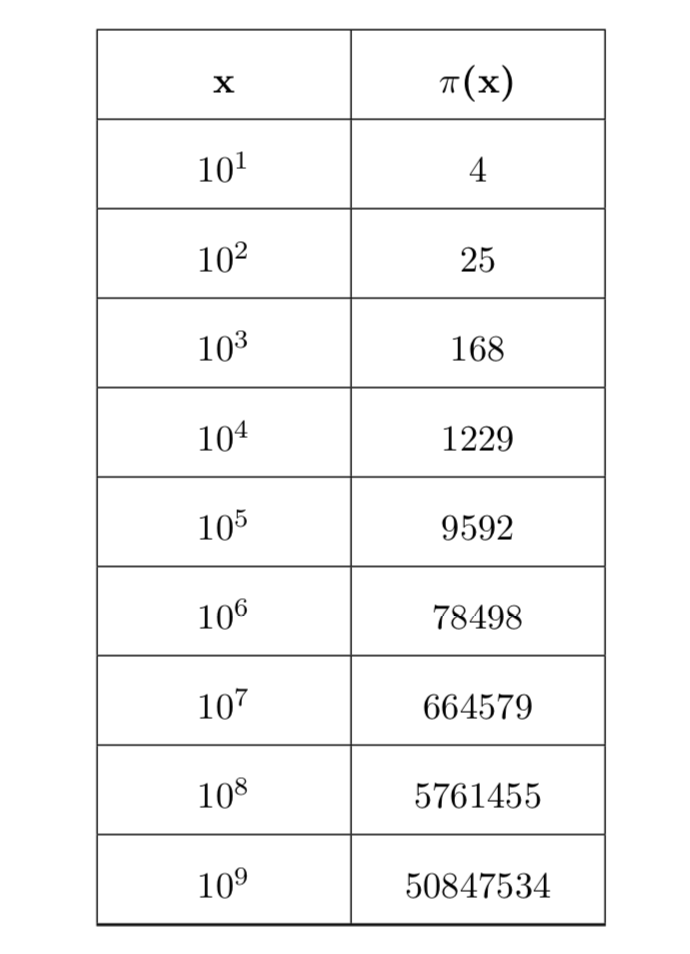
\[ \begin{array}{l} \pi(2)=1 \\ \pi(4) = 2 \\ \pi(10)=4 \\ \pi(20)=8 \\ \pi(50)= 15 \end{array} \]La seguente tabella contiene i valori della funzione per alcune potenze di \(10\):
I primi studi delle proprietà dei numeri risalgono agli antichi Greci. Già nel \(600\) A.C. la scuola pitagorica classificava i numeri naturali come pari, dispari e composti. Tuttavia i risultati più importanti e significativi apparvero negli Elementi di Euclide, intorno al \(300\) A.C. Uno dei teoremi più importanti dimostrati da Euclide è l’esistenza di infiniti numeri primi.
La distribuzione dei numeri primi è estremamente irregolare ed ha eluso per diversi secoli gli sforzi dei migliori matematici. Un risultato fondamentale per comprendere la distribuzione dei numeri primi è il famoso Teorema dei numeri primi, dimostrato quasi contemporaneamente nel \(1896\) dai matematici Hadamard e de la Vallée Poussin. L’enunciato del teorema è il seguente:
I fattori principali che hanno portato alla dimostrazione del Teorema dei numeri primi sono i seguenti:
- i contributi di Eulero, tra cui l’introduzione della funzione zeta di Riemann, seppure limitata al caso reale;
- le congetture di Legendre e Gauss sulla distribuzione della funzione \(\pi(x)\);
- i teoremi di Chebyshev;
- i contributi di Riemann, in particolare la sua idea geniale di estendere lo studio della funzione zeta nel campo complesso.
Il grande matematico norvegese Abel (1802-1829) definì questo come il più importante teorema di tutta la Matematica. La dimostrazione originale utilizza strumenti matematici avanzati. Nel \(1949\) i matematici Erdos e Selberg hanno fornito una dimostrazione che non utilizza gli strumenti dell’analisi complessa. Questo tipo di dimostrazione viene chiamata ‘elementare‘ anche se in realtà è molto lunga e complessa.
Per una dimostrazione che utilizza i metodi dell’analisi complessa vedere [1], mentre per una dimostrazione elementare vedere [2].
2) L’insieme dei numeri primi è infinito
I numeri primi sono considerati i mattoni della matematica. Questo è dovuto al teorema fondamentale dell’aritmetica, secondo il quale ogni numero naturale può essere rappresentato in modo univoco come prodotto finito di potenze di primi distinti:
\[ n= p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{k}^{a_{k}} =\prod\limits_{i=1}^{k}p_{i}^{a_{i}} \]La decomposizione è unica, a parte l’ordine dei fattori.
La prima dimostrazione rigorosa del teorema si trova nell’opera fondamentale di Gauss ‘Disquisitiones Arithmeticae‘ del \(1801\).
Tuttavia già gli antichi Greci e anche gli altri popoli che studiavano la matematica sostanzialmente erano consapevoli del teorema, anche senza darne dimostrazione formale. Infatti lo studio delle proprietà dei divisori di un intero e dei numeri perfetti porta direttamente alla conclusione che un intero può essere fattorizzato mediante prodotto di numero primi.
Nel Libro VII degli ‘Elementi’ di Euclide, nella proposizione \(30\), viene enunciato quello che oggi è conosciuto come il lemma di Euclide, che in forma moderna è il seguente:
Lemma di Euclide
Dato un numero primo \(p\) e due interi \(a,b\), se \(p\) divide il prodotto \(ab\), allora \(p\) divide \(a\) oppure \(p\) divide \(b\). In simboli
Dimostrazione
Il lemma di Euclide può essere dimostrato mediante l’identità di Bezout, che deriva direttamente dall’algoritmo di Euclide per il calcolo del massimo comune divisore di due interi. L’identità di Bezout dice che dati due interi \(a,b\), tali che \((a,b)=d\), allora esistono due interi \(x,y\) tali che
Torniamo ora al lemma di Euclide. Supponiamo che \((a,p)=1\) (altrimenti avremmo finito). Per l’identità di Bezout esistono interi \(x,y\) tali che \(ax+py=1\). Moltiplicando entrambi i membri per \(b\) abbiamo
\[ abx+pby = b \]Ora \(p\) divide \(abx\) per ipotesi e naturalmente divide anche \(pby\). Quindi \(p\) divide anche \(b\).
Mediante il lemma di Euclide si dimostra facilmente il teorema fondamentale dell’aritmetica.
Negli Elementi di Euclide viene utilizzato il linguaggio geometrico anche per le dimostrazioni relative alla teoria dei numeri. Seguire le dimostrazioni originali di Euclide è molto istruttivo e interessante. Un ottimo sito per studiare gli Elementi di Euclide è claymath.org.
Teorema 2.1 – Euclide
L’insieme dei numeri primi è infinito.
Esistono diverse dimostrazioni del teorema di Euclide. Vediamone alcune.
Dimostrazione di Euclide
Euclide utilizza il metodo di dimostrazione per assurdo. Egli assume l’ipotesi che il numero dei primi sia finito e con un ragionamento elegante giunge ad una contraddizione.
Supponiamo che esistano solo \(n\) numeri primi \(p_{1},p_{2},\cdots,p_{n}\), con \(n\) finito. Ora consideriamo il numero naturale
Come ogni numero naturale \(x\) deve avere un divisore primo. Tuttavia non è divisibile da nessuno dei primi \(p_{1}, \cdots,p_{n}\), in quanto il resto della divisione non è uguale a zero. Quindi esiste almeno un altro numero primo, oltre gli \(n\) dell’ipotesi. Questo ragionamento può essere ripetuto all’infinito, e quindi il numero dei primi non può essere finito.
Il risultato di Euclide può anche essere espresso in questa forma:
Sia \(n\) un numero naturale maggiore di \(2\). Allora esiste almeno un numero primo \(p\) tale che
Dimostrazione di Stieltjes
Sia dato un qualunque insieme finito di numeri primi \(p_{1}, p_{2}, … ,{p_n}\) il cui prodotto sia \(x = p_{1}p_{2}…p_{n}\). Sia \(x=ab\) una qualunque fattorizzazione di \(x\). Allora ognuno dei numeri \(p_{i}\) divide \(a\) oppure \(b\), ma non può dividere entrambi. Quindi nessuno dei \(p_{i}\) divide la somma \(a+b\). Quindi deve esistere almeno un altro numero da aggiungere all’insieme originale.
Dimostrazione di Goldbach
Definiamo la seguente successione di numeri interi \(x_{n}\):
Chiaramente i numeri \(x_{n}\) sono tutti dispari. Mediante il metodo di induzione si trova la seguente espressione
\[ x_{n}=2^{2^{n-1}}+1 \]I numeri \(x_{n+1}\) sono chiamati numeri di Fermat e sono indicati con il simbolo \(F_{n}\). La dimostrazione di Goldbach si basa sulla seguente proprietà dei numeri di Fermat:
Teorema 2.2
I numeri di Fermat sono tutti dispari e non hanno divisori comuni, cioè
Dimostrazione
Il teorema si dimostra facilmente osservando che se esistesse un intero \(m \gt 1\) tale che
allora in base alla definizione dei numeri di Fermat dovrebbe risultare \(m |2\), ma questo non è possibile in quanto i numeri \(F_{n}\) sono tutti dispari.
Quindi, essendo i numeri di Fermat infiniti, anche i numeri primi devono essere infiniti.
I valori iniziali dei numeri di Fermat sono i seguenti:
Come si può notare si tratta di tutti numeri primi. Da questo Fermat fece l’ipotesi che tutti i numeri di Fermat sono primi. Nel \(1732\), circa \(70\) anni dopo la morte di Fermat, Eulero riuscì a calcolare il valore di \(F_{5}\), confutando l’ipotesi di Fermat:
\[ F_{5}=2^{2^{5}}+1=641 \cdot 6700417 \]La congettura di Fermat non si è rivelata molto fortunata. Tutti i numeri di Fermat calcolati da \(F_{5}\) a \(F_{32}\) sono composti.
3) I crivelli di Eratostene e Legendre
Due problemi di fondamentale importanza sono i seguenti:
- dato un intero positivo \(n\), riconoscere se è un numero primo o composto;
- dato un intero positivo composto \(n\), trovare la sua scomposizione in fattori primi.
L’importanza di questi problemi è stata sottolineata da Gauss nella sua opera fondamentale ‘Disquisitiones Arithmeticae‘ con le seguenti parole:
“Il problema di distinguere i numeri primi dai composti e di decomporre i secondi nei loro fattori primi è conosciuto essere uno dei più importanti e utili in Aritmetica.”
Dato un insieme di numeri \(X\), un crivello è una procedura per contare il numero di elementi di \(X\) che hanno certe proprietà. Il crivello elimina gli elementi non buoni lasciando solo quelli che soddisfano le proprietà. Le proprietà possono essere di molti tipi: numeri pari, numeri dispari, numeri divisibili per \(5\), ecc.
3.1) Il crivello di Eratostene
Il crivello di Eratostene è un semplice ed efficace algoritmo ideato dal matematico greco Eratostene (276 – 194 a.c.) per individuare tutti i numeri primi minori di un fissato numero intero positivo.
Ricordiamo che Eratostene è stato un importante scienziato che, tra le altre cose, con un esperimento ingegnoso è riuscito per la prima volta a misurare le dimensioni della Terra, con un sufficiente grado di precisione per l’epoca.
L’algoritmo di Eratostene permette di determinare tutti i numeri primi minori od uguali ad un certo numero positivo \(x\). I passi dell’algoritmo sono i seguenti:
- fare una lista di tutti gli interi positivi dell’intervallo \([2,x]\);
- lasciare il numero \(2\) ed eliminare tutti i multipli propri di \(2\) (\(2\) è l’unico numero primo pari);
- fare la stessa cosa con il numero \(3\);
- scegliere ogni volta il prossimo numero piccolo non cancellato ed eliminare tutti i suoi multipli propri;
- ripetere la procedura fino ai numeri che non superano \(\sqrt{x}\).
Alla fine i numeri rimanenti nella lista sono tutti i numeri primi minori od uguali a \(x\).
Esercizio 3.1
Dimostrare che se \(n\) è composto, allora deve avere un fattore primo \(p \le \sqrt{n}\).
L’algoritmo di Eratostene è semplice e facile da implementare con un programma; tuttavia per valori molto grandi di \(n\) diventa poco efficiente, anche con i computer più potenti.
Oggi esistono algoritmi più sofisticati che grazie a computer sempre più potenti possono fattorizzare numeri interi con molte cifre (\( \gt 100)\).
Nella tabella seguente possiamo vedere una semplice applicazione dell’algoritmo per trovare i numeri primi inferiori a \(20\). Come si vede bastano due passi dell’algoritmo: i numeri non colorati nella terza riga sono i primi compresi nell’intervallo.

3.2) Il crivello di Legendre
Dopo il crivello di Eratostene sono stati elaborati altri metodi per riconoscere i numeri primi. Il più semplice è quello di Legendre che dà un modo per calcolare \(\pi(N)\) a partire dalla conoscenza esplicita dei primi nell’intervallo\([1,\sqrt{N}]\). L’idea base è la stessa di Eratostene: un numero composto minore di \(N\) deve essere divisibile da un numero primo minore di \(\sqrt{N}\).
Riprendiamo il crivello di Eratostene. Contiamo il numero di interi positivi minori od uguali a \(x\) che rimangono dopo aver eliminato i multipli di tutti i primi che non superano \(\sqrt{x}\). Per indicare questo numero usiamo la funzione \(\pi(x,\sqrt{x})\):
Notare che \(\pi(x,\sqrt{x})\) conta anche il numero \(1\).
Esercizio 3.2
Dimostrare le seguenti formule:
Teorema 3.1 – Legendre
\[ \pi(x,\sqrt{x}) = \lfloor x \rfloor – \sum\limits_{p_{1}\le \sqrt{x}} \Big\lfloor \frac{x}{p_{1}}\Big\rfloor + \cdots + (-1)^{k}\sum\limits_{p_{1}\lt \cdots \lt p_{k}\le \sqrt{x}} \Big\lfloor \frac{x}{p_{1} \cdots p_{k}}\Big\rfloor \]dove \(k=\pi(\sqrt{x})\).
Se poniamo \(P= \prod\limits_{p \le \sqrt{x}}\) possiamo scrivere in forma compatta, utilizzando la funzione di Möbius:
\[ \pi(x,\sqrt{x}) = \sum\limits_{d|P} \mu(d)\Big\lfloor \frac{x}{d}\Big\rfloor \]Ricordiamo la definizione della formula di Möbius:
\[ \mu(n)= \begin{cases} (-1)^{k} \quad \text{se } n=\prod\limits_{i=1}^{k} p_{i} \\ 0 \quad \text{ altrimenti} \end{cases} \]Dimostrazione
La dimostrazione del teorema di Legendre segue facilmente applicando il principio di inclusione-esclusione (vedi articolo in questo sito).
Il totale degli interi minori od uguali a \(x\) è uguale a \(\lfloor x \rfloor\). Se da questo togliamo il numero dei multipli dei primi \(p_{1}\), con \(p_{1} \le \sqrt{x}\), abbiamo
Questa espressione conta bene gli interi con al massimo un divisore primo \(p \le \sqrt{x}\), ma gli interi con due o più fattori primi \(p \le \sqrt{x}\) vengono sottratti due volte. Per questo dobbiamo aggiungere un ulteriore elemento
\[ \lfloor x \rfloor – \sum\limits_{p_{1} \le \sqrt{x}} \Big\lfloor \frac{x}{p_{1}} \Big\rfloor + \sum\limits_{p_{1} \lt p_{2}\le \sqrt{x}} \Big\lfloor \frac{x}{p_{1}p_{2}} \Big\rfloor \]Ora gli interi divisibili da tre fattori primi \(p \le \sqrt{x}\) sono sommati troppe volte. Quindi dobbiamo aggiungere un altro elemento. Procedendo in questo modo otteniamo la formula di Legendre.
In definitiva possiamo scrivere la formula di Legendre per contare i numeri primi:
\[ \begin{array}{l} \pi(x) = \pi (\sqrt{x})- 1 + \pi(x,\sqrt{x}) \end{array} \]Esempio 3.1
Supponiamo \(x=100\). Possiamo verificare facilmente che \(\pi(100)=25\). Ora calcoliamo questo valore mediante la formula di Legendre.
I numeri primi minori o uguali \(10=\sqrt{100}\) sono \(2,3,5,7\). Quindi \(P=210\). I divisori di \(210\) minori od uguali a \(100\) per i quali la funzione di Möbius non è nulla (divisori liberi da quadrati) sono i seguenti:
Facendo i calcoli otteniamo
\[ \pi(100,10) = \sum\limits_{d|210} \mu(d)\Big\lfloor \frac{100}{d}\Big\rfloor = 22 \]Quindi mediante la formula di Legendre possiamo calcolare il numero dei primi inferiori a \(100\):
\[ \begin{array}{l} \pi(100) = \pi (10)- 1 + \pi(100,10)= 4 -1 +22= 25 \end{array} \]3.3) Il crivello di Brun e i primi gemelli
Il crivello di Legendre ha dei limiti: gli errori dovuti al numero molto grande dei termini frazionari della somma
\[ \pi(x,\sqrt{x}) = \sum\limits_{d|P} \mu(d)\Big\lfloor \frac{x}{d}\Big\rfloor \]si accumulano e in diversi casi non si possono avere stime precise.
Esistono altri crivelli più efficienti che hanno permesso di ottenere importanti risultati. Tra questi molto importante è il crivello di Brun. Questi crivello è stato creato dal matematico norvegese Viggo Brun (1885-1978) per risolvere alcuni problemi di teoria dei numeri, in particolare il problema dei primi gemelli.
In questa sede non entriamo in dettaglio sul crivello di Brun, il quale è abbastanza complesso. Ci limitiamo a ricordare due risultati importanti ottenuti da Brun relativamente al problema dei numeri primi gemelli.
Due numeri primi si dicono gemelli se sono una coppia del tipo \((p,p+2)\). Ad esempio sono primi gemelli le seguenti coppie:
Il problema non ancora risolto è se esistono infinite coppie di primi gemelli oppure soltanto un numero finito.
Teorema 3.2 – Brun
Indichiamo con \(\pi_{2}(x)\) il numero delle coppie \((p,p+2)\) di primi gemelli, tali che \(p \le x\). L’ordine di grandezza della funzione \(\pi_{2}(x)\) è
dove il simbolo di Landau \(f(x)=O(g(x))\) significa che esiste una costante positiva tale che al crescere di \(x\) si ha definitivamente \(f(x) \le K g(x)\), con \(f,g\) funzioni a valori positivi.
Come conseguenza del teorema di Brun si ha questo importante corollario:
Corollario del teorema di Brun
La serie dei reciproci dei primi gemelli
converge ad un numero finito.
La \(B\) viene chiamata la costante di Brun.
Mediante calcoli al computer si è determinato un valore approssimato della costante
Naturalmente il fatto che la serie converga non esclude che le coppie di primi gemelli siano infinite. Quindi il problema dei primi gemelli rimane tuttora non risolto.
Per la dimostrazione del teorema di Brun vedere [9].
4) Pierre de Fermat (1601-1665)
Dopo i Greci, lo studio dei numeri primi riprese soltanto nel secolo XVII, grazie soprattutto a Fermat, il quale è stato uno dei matematici più importanti del periodo. Fermat ha dato rilevanti contributi alla nascita del Calcolo delle Probabilità, della Geometria Analitica e del Calcolo Differenziale e Integrale. La sua passione per la Teoria dei Numeri deriva in particolare dalla lettura dell’edizione del 1621 della Arithmetica di Diofanto, tradotta a Parigi in latino.
In questa sede ricordiamo soltanto alcuni dei suoi contributi. In primo luogo il seguente teorema:
Teorema 4.1 – Piccolo teorema di Fermat
Se \(p\) è un numero primo e \(a\) un intero primo con \(p\) allora
In generale vale la seguente relazione, anche se \(a\) non è primo con \(p\)
\[ a^{p} \equiv a \pmod{p} \]Per la dimostrazione vedere l’articolo in questo sito.
Il teorema di Fermat può essere utulizzato per determinare se un intero \(n\) è primo oppure no. Vale infatti il seguente criterio:
Criterio di primalità di Fermat
Se esiste un intero \(a\) primo con \(n\) tale che risulti
allora il numero \(n\) è un numero composto.
Tuttavia non possiamo affermare il contrario: esistono degli interi \(n\) non primi per i quali la congruenza \(a^{n-1} \equiv 1 \pmod{n}\), con \((a,n)=1\), è sempre vera. Questi si chiamano numeri di Carmichael.
Se escludiamo i numeri di Carmichael il test di Fermat è abbastanza buono dal punto di vista probabilistico. Vale infatti il seguente:
Teorema 4.2
Se \(n\) è un numero composto e non è un numero di Carmichael, allora almeno metà dei numeri \(a\) primi con \(n\) soddisfano \(a^{n-1} \not\equiv 1 \pmod{n}\).
Dimostrazione
Supponiamo che esista un \(b\) tale che \((b,n)=1\) e \(b^{n-1} \equiv 1 \pmod{n}\). Se \(n\) non è un numero di Carmichael allora esiste un \(a\) con \((a,n)=1\) e \(a^{n-1} \not\equiv 1 \pmod{n}\). Da questo deriva
Poiché \( ab \neq a\), a fronte di un elemento \(a\) che verifica la congruenza ne esiste almeno un altro \(ab\) che non la verifica.
Se un numero è composto la probabilità che la congruenza sia vera è quindi \(\le \frac{1}{2}\). La probabilità di errore, cioè di assumere che \(n\) è primo quando in realtà è composto, può essere resa piccola a piacere ripetendo l’algoritmo. Ad esempio ripetendo l’algoritmo \(k\) volte, cambiando in modo casuale la base \(a\),la probabilità di errore può essere resa minore di \(\dfrac{1}{2^{k}}\).
Un altro contributo importante di Fermat è il suo metodo per fattorizzare un intero.
Metodo di fattorizzazione di Fermat
Supponiamo di poter rappresentare un intero dispari \(n\) come differenza di due quadrati:
Se nessuno dei fattori è uguale a \(1\), allora abbiamo trovato una fattorizzazione di \(n\).
Notiamo che un intero \(n=xy\) si può sempre rappresentare come differenza di due quadrati:
In genere si procede per tentativi. Poniamo \(x_{1}=\lceil \sqrt{n}\rceil\), il più piccolo intero maggiore o uguale alla radice quadrata di \(n\). Quindi verifichiamo se il numero
\[ x=x_{1}^{2}- n \]è un quadrato. Se sì abbiamo finito, altrimenti proviamo con \(x_{1}+1\) e così via.
Esercizio 4.1
Fattorizzare il numero \(n=1729\).
In questo caso \(x_{1}=42\). L’espressione \(42^{2}-1729=35\) non è un quadrato. Dobbiamo provare fino al numero \(x=55\) per ottenere
\[ 55^{2}-1729=1296=36^{2} \]La fattorizzazione di \(1729\) è quindi:
\[ 1729 =(55+36)(55-36)=91 \cdot 19 \]Il metodo di Fermat funziona bene se i fattori sono vicini alla radice quadrata del numero, altrimenti può essere molto lento.
Sono state create diverse varianti dell’algoritmo di Fermat per renderlo più efficiente. Nonostante la sua semplicità l’idea di Fermat è alla base dei moderni algoritmi di fattorizzazione: il crivello quadratico e il crivello dei campi di numeri generale.
Per approfondire lo studio dell’algoritmo di Fermat vedere [7].
5) Eulero e la nascita della teoria analitica dei numeri
“I matematici hanno cercato invano di scoprire un qualche ordine nella successione dei numeri primi, e abbiamo ragione di credere che è un mistero che la mente umana non potrà mai penetrare.” (Eulero)
Dopo Fermat, lo studio della Teoria dei Numeri è stato portato avanti da Eulero (1703-1783). La produzione matematica di Eulero in molti settori della matematica è enorme. Nel campo della Teoria dei Numeri ha dimostrato importanti teoremi e i suoi risultati hanno permesso di iniziare a svelare il mistero della distribuzione dei numeri primi. Eulero ha permesso un avanzamento della Teoria dei Numeri in diverse direzioni: funzioni aritmetiche, reciprocità quadratica, teoria delle partizioni, distribuzione dei numeri primi. In questo articolo ci limiteremo ad accennare ai suoi contributi relativi all Teoria Analitica dei Numeri e in particolare alla distribuzione dei numeri primi.
I contributi di Eulero sono stati possibili grazie agli strumenti potenti dell’Analisi Matematica che ebbero un grande sviluppo grazie a Newton, Leibniz e ad Eulero stesso: il calcolo differenziale e integrale, la teoria delle serie e dei prodotti infiniti, lo sviluppo delle funzioni in serie di Taylor, ecc. Un primo risultato che rese famoso Eulero è la soluzione del problema di Basilea, cioè il calcolo della serie
Per una dimostrazione vedere l’articolo in questo sito.
5.1) Il prodotto di Eulero e la funzione zeta
Uno dei maggiori contributi di Eulero è l’introduzione di una funzione molto importante nella Teoria dei Numeri, che in seguito verrà chiamata funzione zeta di Riemann. Nel \(1737\) Eulero dimostrò il seguente teorema:
Teorema 5.1 – Il prodotto di Eulero
\[ \zeta(s) =\sum\limits_{n=1}^{\infty}\frac{1}{n^{s}}=\prod\limits_{p}^{}\frac{1}{\left(1- p^{-s}\right)} \quad s \gt 1 \]dove \(s\) è un numero reale maggiore di \(1\) e il prodotto infinito è su tutti i numeri primi.
La funzione \(\zeta(s)\) studiata da Eulero per valori reali di \(s\), verrà in seguito estesa ai numeri complessi e prenderà il nome di funzione zeta di Riemann.
Dimostrazione
Consideriamo un singolo elemento del prodotto infinito
La serie è assolutamente convergente per \(s \gt 0\). Moltiplichiamo un numero finito di fattori
\[ \prod\limits_{p \le x}{}\frac{1}{1-p^{-s}}=\prod\limits_{p \le x}{}\left(1+\frac{1}{p^{s}} + \frac{1}{p^{2s}} + \cdots \right) \]Grazie alla convergenza assoluta possiamo riordinare gli elementi del prodotto come vogliamo, senza cambiare il valore. Per il teorema di fattorizzazione unica degli interi abbiamo
\[ \prod\limits_{p \le x}{}\frac{1}{1-p^{-s}}=\sum\limits_{n \in T_{x}}\frac{1}{n^{s}} \]dove \(T_{x}\) è l’insieme di tutti gli interi i cui fattori primi sono minori od uguali a \(x\). Ovviamente si ha
\[ \sum\limits_{n \in T_{x}}\frac{1}{n^{s}} \gt \sum\limits_{n \le x}\frac{1}{n^{s}} \]e quindi
\[ 0 \lt \sum\limits_{n =1}^{\infty}\frac{1}{n^{s}} – \sum\limits_{n \in T_{x}}\frac{1}{n^{s}} \lt \sum\limits_{n \gt x}\frac{1}{n^{s}} \]Poiché la serie \(\sum\limits_{n=1}^{\infty}\dfrac{1}{n^{s}}\) converge per \(s \gt 1\) l’ultima serie tende a zero quando \( x \to \infty\) e quindi
\[ \sum\limits_{n=1}^{\infty}\frac{1}{n^{s}}= \lim_{x \to \infty}\prod\limits_{p \le x}{}\frac{1}{1-p^{-s}}=\prod\limits_{p}^{}\frac{1}{1- p^{-s}} \]5.2) Dimostrazione di Eulero che i numeri primi sono infiniti
La formula di Eulero è valida solo per \(s \gt 1\). Tuttavia Eulero cercò di utilizzare la formula anche nel caso uguale a \(1\), ottenendo una ulteriore dimostrazione dell’esistenza di infiniti primi. Se nel prodotto di Eulero poniamo \(s=1\) abbiamo la seguente identità:
\[ \sum\limits_{n=1}^{\infty}\frac{1}{n}=\prod\limits_{n=1}^{\infty}\left(1- \frac{1}{p}\right) \]Poiché la serie armonica diverge, ne segue che devono esistere infiniti primi. Chiaramente, presa alla lettera la dimostrazione di Eulero non è valida, in quanto la somma armonica è divergente e quindi la formula di Eulero non vale nel caso \(s=1\). Tuttavia la dimostrazione può essere resa rigorosa partendo dalla formula valida con \(s \gt 1\), e calcolando il limite per \(s \to 1\) dalla parte destra. Se il numero di primi fosse finito allora il prodotto avrebbe un valore finito, mentre la somma assumerebbe valori grandi a piacere.
In un articolo successivo studieremo altri importanti contributi di Eulero sulla distribuzione asintotica dei numeri primi, che anticiperanno il teorema dei numeri primi.
6) Alcune proprietà elementari della successione dei primi
Il teorema di Euclide sull’infinità dei numeri primi può essere espresso in questa forma:
\[ \lim_{x \to \infty}\pi(x) = \infty \]Naturalmente una funzione \(y=f(x)\) può tendere all’infinito con diversi tassi di crescita. Vediamo alcuni esempi:
\[ \begin{array}{l} y = x \quad \text{lineare} \\ y = \ln x \quad \text{logaritmico} \\ y = x^{2} \quad \text{quadratico } \\ y = e^{x} \quad \text{esponenziale} \\ \end{array} \]Analizziamo ora la crescita della funzione \(\pi(x)\) rispetto alla funzione lineare \(x\). Ricordiamo la definizione della funzione di Eulero \(\varphi(n)\):
\[ \varphi (n) = |\{x\in \mathbb{N} \mid 1\leq x\leq n, (x,n)=1\}| \]La funzione di Eulero quindi conta gli interi contenuti nell’intervallo \([1,n]\), che sono primi con \(n\). Ricordiamo che se \(n=p_1^{a_1}\cdots p_k^{a_k}\), allora
\[ \varphi(n)=\prod_{i=1}^kp_i^{a_i-1}(p_i-1) = n \cdot \prod_{i=1}^{k} \left( 1- \frac{1}{p_{i}}\right) \]Teorema 6.1
Fissato un intero positivo \(n\), si ha
Dimostrazione
In base all’algoritmo di divisione euclideo possiamo scrivere \(\lfloor x \rfloor =nq+r\) con \(0 \le r \lt n\). Dividiamo gli interi compresi in \([1,x]\) in \(q\) sottoinsiemi di \(n\) interi consecutivi, più un insieme rimanente contenente gli \(r\) interi \(qn+1, \cdots, qn+r\).
Nell’insieme degli interi \(\{1,2, \cdots,n\}\) ci sono al massimo \(n\) primi. Nell’insieme \(\{n+1,\cdots,2n\}\) ci sono al massimo \(\varphi(n )\) primi, poiché ogni intero non primo con \(n\) ha un fattore primo in comune con \(n\) minore od uguale a \(n\). In modo simile gli altri gruppi di \(n\) interi hanno al massimo \(\varphi(n)\) numeri primi. Quindi abbiamo:
Dividendo per \(x\) otteniamo il risultato del teorema.
Teorema 6.2
Sia \(T \gt 1\) e siano \(p_{1},p_{2},\dots,p_{t}\) tutti i primi contenuti nell’insieme \(\{1,2,\cdots,T\}\). Allora si ha
La dimostrazione è simile a quella della formula di Eulero. Si sviluppano i fattori del prodotto mediante la serie geometrica e si effettuano i prodotti delle serie ottenute, utilizzando il teorema fondamentale dell’aritmetica.
Dal teorema precedente segue facilmente il seguente:
Teorema 6.3
La serie dei reciproci dei primi è divergente:
Dimostrazione
Dal teorema precedente, se \(T \to \infty\), poiché la serie armonica tende all’infinito, abbiamo
Questo significa che deve essere \(\sum\limits_{1}^{\infty } \dfrac{1}{p_{i}}=\infty\), in base ad una nota proprietà dei prodotti infiniti. Per uno studio delle serie e dei prodotti infiniti vedere l’ottimo libretto di Knopp[8].
Teorema 6.4
\[ \lim_{x \to \infty}\frac{\pi(x)}{x} =0 \]Dimostrazione
In base al teorema 6.1 basta dimostrare che \(\lim\limits_{n \to \infty}\dfrac{\varphi(n)}{n}=0\). Dato un \(t \gt 0\) poniamo \(n_{t}=\prod\limits_{p \le t}p\). Abbiamo
Abbiamo sfruttato la disuguaglianza \(e^{x} \ge 1+x\). Il simbolo \(\exp(x)\) è equivalente a \(e^{x}\). Poiché la serie dei reciproci dei primi \(\sum\limits_{p}\dfrac{1}{p}\) è divergente, il limite sopra tende a zero.
I numeri primi dispari possono essere soltanto della forma \(4n+1\) oppure \(4n-1\). Osserviamo che \(4n+1\) è equivalente a \(4n-3\) e \(4n-1\) è equivalente a \(4n+3\).
Per queste due categorie di primi valgono i seguenti teoremi.
Teorema 6.5
Esistono infiniti primi della forma \(4n-1\).
Dimostrazione
Supponiamo che esista solo un numero finito di tali primi; sia \(p\) il maggiore e poniamo
Il numero \(3 \cdot 5 \cdot p\) contiene tutti fattori dispari. Poiché \(N \gt p\) è del tipo \(4n-1\), non può essere primo. Tuttavia nessuno numero primo \(\le p\) divide \(N\), quindi i suoi fattori primi devono essere tutti maggiori di \(p\). Tuttavia i fattori non possono essere tutti del tipo \(4n+1\) poiché il prodotto di due di tali fattori è sempre dello stesso tipo. Ne segue che deve esistere almeno un fattore di \(N\) del tipo \(4n-1\). Abbiamo quindi una contraddizione.
Si può anche dimostrare il seguente teorema:
Teorema 6.6
Esistono infiniti primi della forma \(4n+1\).
Dimostrazione
Consideriamo il numero dispari \(x=(n!)^{2}+1\), con \(n \gt 1\). Essendo dispari sicuramente ha un fattore primo \(p\) maggiore di \(n\) della forma \(4k+1\) oppure della forma \(4k+3\). Supponiamo che \(p=4k+3\). Ricordiamo la seguente relazione elementare
Si ha quindi \((n!)^{2}+1|(n!)^{2(2k+1)}+1\). Abbiamo \(2(2k+1)=p-1\) e quindi poiché \(p|(n!)^{2}+1\) abbiamo \(p|(n!)^{p-1}+1\), da cui segue \(p|(n!)^{p}+n!\). Per il teorema di Fermat \(p|(n!)^{p}-n!\), e quindi \(p|2n!\), ma questo non è possibile perché \(p\) è dispari. Quindi \(p\) deve essere della forma \(4k+1\). Scegliendo valori di \(n\) sempre più grandi ne deriva che devono esistere infiniti numeri primi della forma \(p=4k+1\).
I teoremi precedenti sono casi particolari di un teorema molto importante dimostrato da Dirichlet (1805-1859).
Teorema 6.7 – Dirichlet
Se \(a,b\) sono due interi positivi primi fra loro, allora esistono infiniti numeri primi nella progressione aritmetica
Per una dimostrazione vedere il testo di Apostol [1].
Definizione 6.1
Dato un numero reale positivo \(x\) indichiamo con \(\pi_{1}(x)\) il numero dei primi della forma \(4n+1\) minori od uguali a \(x\), e con \(\pi_{3}(x)\) il numero dei primi della forma \(4n+3\) minori od uguali a \(x\).
Il matematico inglese Hardy (1877-1947) ha dimostrato il seguente importante teorema:
Teorema 6.8
Esistono infiniti numeri reali \(x\) tali che \(\pi_{1}(x) \lt \pi_{3}(x)\) e infiniti numeri reali \(x\) tali che \(\pi_{1}(x) \gt \pi_{3}(x)\).
7) Alcune formule per generare numeri primi
7.1) Il polinomio di Eulero
Un problema che possiamo porci è trovare una funzione in grado di generare tutti i numeri primi oppure che assuma soltanto numeri primi. Un esempio importante è il seguente polinomio di secondo grado proposto da Eulero:
\[ f(x)= x^{2}+ x + 41 \]Questo polinomio produce \(40\) numeri primi sostituendo al posto della variabile \(x\) gli interi \(0,1,2, \cdots, 39\). La formula dà un valore composto con \(x=40\), in quanto \(f(40)=1681=41^{2}\). Tuttavia si può osservare utilizzando un computer che la formula produce numeri primi per molti altri valori; ad esempio \(x=42,43,44,45,46\) ecc.
Per quanto riguarda la possibilità di generare infiniti primi mediante un polinomio, vale il seguente teorema:
Teorema 7.1 – Goldbach
Nessun polinomio \(f(n)\), non costante e a coefficienti interi, può assumere valori primi per ogni \(n\), oppure valori primi da un certo \(n\) in poi.
Dimostrazione
Supponiamo di avere un polinomio di grado \(m\):
Possiamo assumere che il coefficiente principale \(a_{0}\) sia positivo e quindi \(\lim_{n \to \infty}f(n)=\infty\). Supponiamo ora che \(f(n)\) assuma un valore primo per ogni \(n \ge n_{0} \). Poniamo \(p=f(n_{0})\). Allora deve essere \(p | f(n_{0}+ kp)\), per ogni intero positivo \(k\). Ma poiché \(f(n) \to \infty\) al crescere di \(n\), deve essere
per \(k\) sufficientemente grande. Quindi \(f(n_{0}+kp)\) è un numero composto, contrariamente alla scelta di \(n_{0}\).
7.2) Il teorema di Wilson
Teorema 7.2 – Wilson
Se \(p\) è un numero primo, allora
Il teorema si dimostra facilmente utilizzando il piccolo teorema di Fermat. Per una dimostrazione combinatoria vedere l’articolo su questo sito.
Esercizio 7.1
Dimostrare che se un intero \(n\) è composto allora non è possibile che \(n|(n-1)!+1\).
Dimostrazione
Se fosse \(d|n\) con \(1 \lt d \lt n\) allora dovrebbe essere
Ma questo è chiaramente impossibile.
Quindi possiamo enunciare il teorema di Wilson in questo modo:
Teorema 7.2
Un intero \(n \gt 1\) è primo se e solo se \(n|(n-1)!+1\).
Possiamo definire la seguente funzione
\[ f(n)= \begin{cases} 1 \quad n=1 \\ \Big\lfloor \cos^{2}\left(\pi \frac{(n-1)!+1}{n}\right) \Big\rfloor \quad n \gt 1 \\ \end{cases} \]dove \(\lfloor x \rfloor\) indica la parte intera di \(x\).
Quindi per il teorema di Wilson abbiamo:
Si tratta di un criterio per riconoscere i numeri primi, naturalmente di poca utilità per numeri grandi.
7.3) La formula di Gandhi
Nel \(1971\) il matematico indiano J.W. Gandhi ha scoperto un formula che in teoria permette di calcolare il primo \(p_{n}\) conoscendo i numeri primi precedenti. La formula è la seguente:
\[ p_{n}=\Big\lfloor 1 – \frac{1}{\ln 2} \ln \left(-\frac{1}{2}+ \sum\limits_{d|P}{} \frac{\mu (d)}{2^{d}-1}\right)\Big\rfloor \]dove \(\mu(n)\) è la funzione di Möbius e \(P=p_{1} \cdots p_{n-1}\) è chiamato il primoriale di \(n-1\).
Anche questa formula è di scarsa utilità pratica, in quanto il termine \(2^{d}\) può raggiungere valori molto alti che non si riescono a calcolare, neanche con i computer più potenti.
7.4) La formula di Mills
Nel \(1947\) W.H. Mills propose la formula seguente: esiste un numero reale, non intero \(\gt 1\) tale che
\[ \lfloor A^{3x} \rfloor \quad x=1,2,3\cdots \]è sempre primo. Nell’articolo Mills non specifica il valore della costante, ma dimostra solo che esiste. Altri autori hanno dimostrato che un valore possibile per la costante è
\[ A \approx 1,3063778838 \cdots \]7.5) Il teorema di Sherck
Per finire questa panoramica ricordiamo un teorema interessante dimostrato da H. J. Sherck nel \(1830\).
Teorema 7.3
Indichiamo con \(p_{n}\) l’ennesimo numero primo in ordine ascendente. Allora valgono le seguenti formule, con scelte opportune dei segni \(\pm\):
Esempio 7.1
\[ \begin{array}{l} p_{6}=1+p_{1}-p_{2}-p_{3}+p_{4}+ p_{5} \\ 13=1+2-3-5+7+11 \end{array} \]Per una dimostrazione vedere il testo di Sierpinski [3].
8) Il polinomio di Matijasevic
Nel \(1970\) il matematico russo Matijasevic ha dimostrato l’esistenza di un polinomio in più variabili tale che i suoi valori positivi sono solo e tutti i numeri primi, mentre assume anche valori composti quando è negativo.
Matijasevic ottenne questo risultato mentre lavorava alla soluzione del decimo problema di Hilbert, presentato alla Conferenza Internazionale di Matematica nel 1900 a Parigi.
Per comprendere il problema di Hilbert ricordiamo il concetto di equazioni diofantee. Un’equazione diofantea è un’equazione in una o più incognite con coefficienti interi, di cui si cercano soluzioni intere.
Esempio 8.1
Il caso più semplice è l’equazione lineare
a coefficienti interi. Se \(x,y\) possono assumere tutti i valori reali, allora l’equazione ha infinite soluzioni reali e sul piano cartesiano rappresenta una retta. Se invece vogliamo solo soluzioni intere allora abbiamo il seguente teorema:
Teorema 8.1
L’equazione \(ax+by=c\) con coefficienti interi ammette soluzioni intere se e solo se \((a,b)|c\).
Per equazioni più complicate di grado maggiore di \(1\) e con più variabili il problema diventa complesso.
Molte equazioni particolari sono state risolte, spesso ricorrendo a procedure ad hoc, non valide in generale. Il problema posto da Hilbert chiedeva di trovare una procedura per determinare se è possibile riconoscere se un’equazione diofantea generica è risolubile oppure no.
“Data un’equazione diofantea con un numero qualsiasi di incognite e con coefficienti numerici interi: trovare un procedimento secondo il quale si può determinare mediante un numero finito di operazioni se l’equazione è risolubile in interi “
La risposta al decimo problema di Hilbert è negativa: Matijasevic, basandosi anche sugli studi portati avanti da Martin Davis e Julia Robinson ha dimostrato che non esiste un algoritmo in grado di rispondere positivamente. In altri termini qualunque algoritmo si trovi per dimostrare l’esistenza di soluzioni per le equazioni diofantee, c’è almeno una equazione per la quale l’algoritmo non funziona.
Una conseguenza dei risultati di Matijasevic è il seguente:
Teorema 8.2
L’insieme dei numeri primi è l’insieme dei valori positivi di un polinomio di grado \(25\) con \(26\) incognite. Il polinomio è il seguente:
Per una panoramica dei \(23\) problemi posti da Hilbert vedere [5]. Per approfondire la dimostrazione di Matijasevich vedere [4].
Il polinomio di Matijasevich, come le frazioni di Conway del paragrafo seguente, sono due tipi generatori di numeri primi assolutamente sorprendenti e interessanti dal punto di vista teorico. Tuttavia non sono chiaramente di pratica utilità.
9) Il linguaggio FRACTRAN e le frazioni di Conway
FRACTRAN è un linguaggio di programmazione molto originale inventato dal matematico John Conway. Un programma FRACTRAN è costituito da una lista di frazioni e da un intero positivo \(n\), che è l’input iniziale del programma.
Le regole del programma sono le seguenti:
- trova la prima frazione \(f = \dfrac{a}{b}\) della lista tale che il prodotto \( n \cdot \dfrac{a}{b}\) è un intero;
- ripeti il passo precedente con il nuovo intero, iniziando sempre dalla prima frazione della lista;
- continua fino a che nessun prodotto fornisce un intero, nel qual caso il programma termina; altrimenti procedi indefinitivamente.
Esempio 9.1
Supponiamo di avere un unica frazione \(\dfrac{7}{6}\) e il valore iniziale sia \(n=1944\). Osserviamo che \(1944=2^{3}3^{5}\). Applicando le regole sopra esposte abbiamo
Questo semplice programma di fatto calcola il minimo fra gli esponenti dei fattori primi \(2,3\) presenti nella fattorizzazione del numero iniziale \(n\). Il valore minimo è l’esponente del numero \(7\) presente al momento della fine del programma.
Esercizio 9.1 – Somma di due interi
Dato il programma che usa la frazione \(f=\dfrac{3}{2}\), con input \(n=2^{a}3^{b}\), dimostrare che nel risultato finale l’esponente del numero \(3\) è la somma \(a+b\).
Esercizio 9.2 – Prodotto di due interi
Data la seguente lista di frazioni
dimostrare che partendo con l’input \(n=2^{a}3^{b}\) il risultato finale è \(5^{ab}\).
Conway ha costruito un programma, chiamato PRIMEGAME, in grado di generare tutti i numeri primi. Il programma utilizza le seguenti \(14\) frazioni:
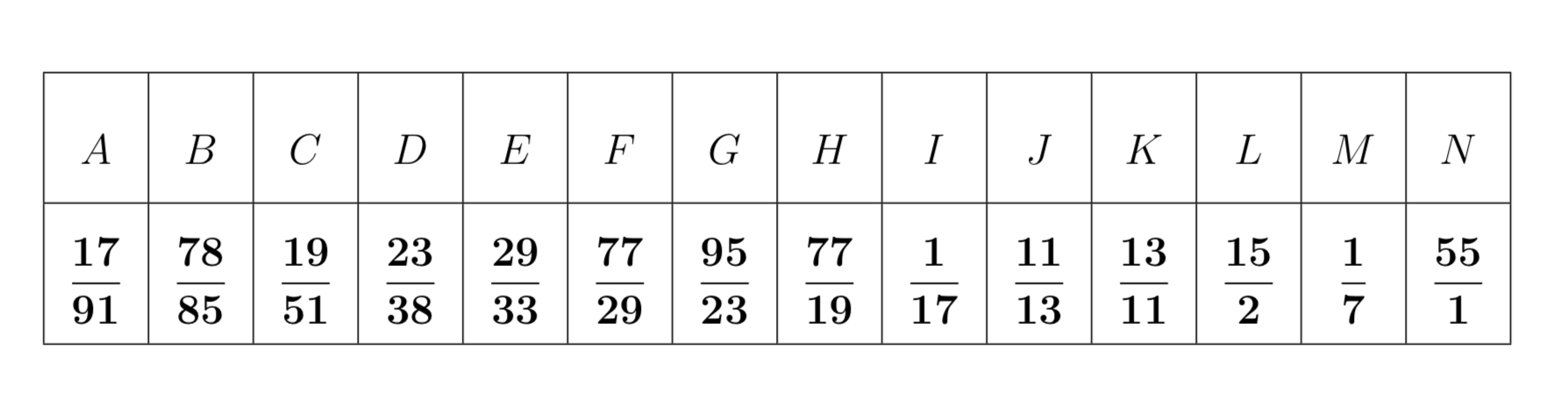
Teorema 9.1 – Conway
Utilizzando le \(14\) frazioni sopra indicate e il valore iniziale \(2\), tra i numeri della sequenza ci sono tutte le potenze di \(2\) i cui esponenti sono i numeri primi in ordine ascendente di grandezza
Dimostrazione
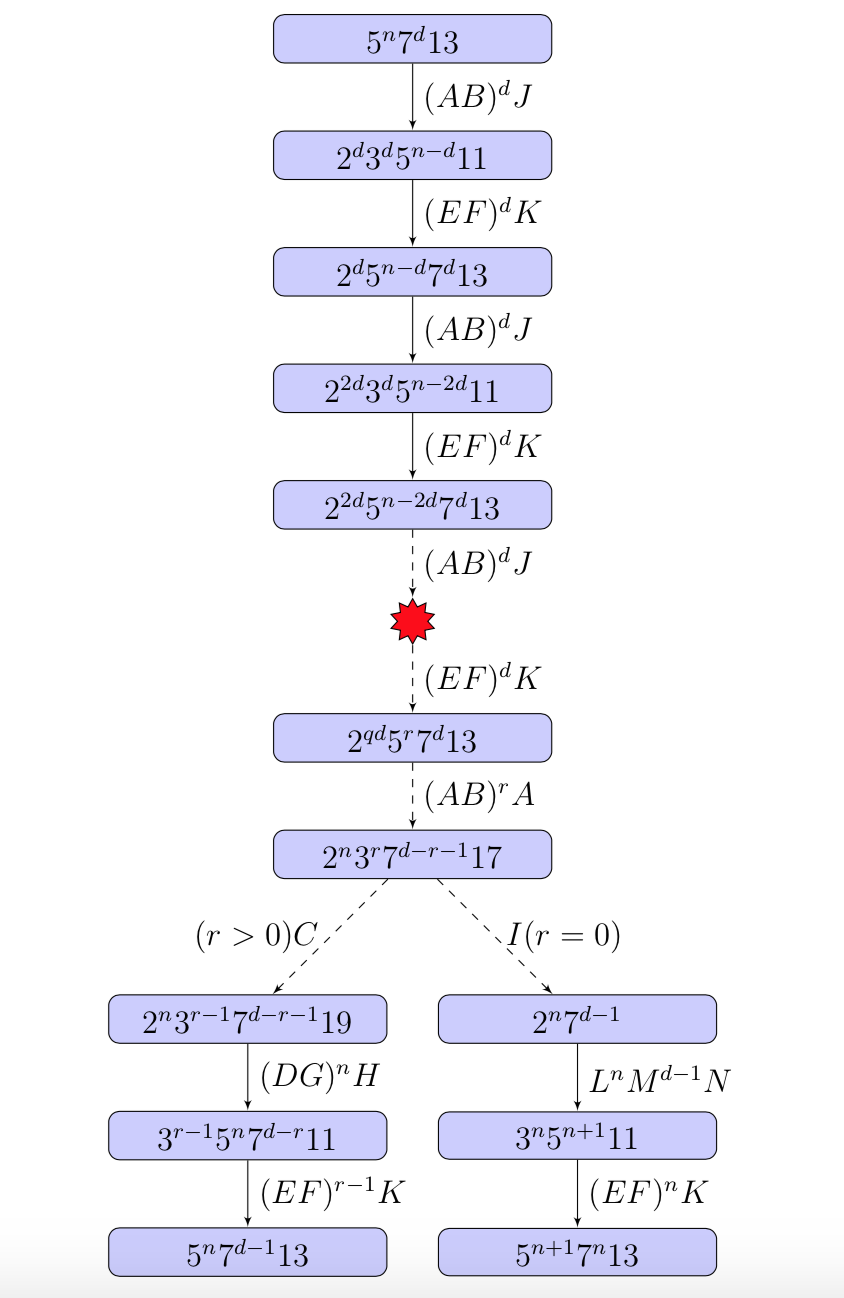
Partendo dal numero \(x=2\), al sesto passo dell’algoritmo si arriva al numero \(x=2275\), la cui fattorizzazione è \(5^{2}\cdot 7 \cdot 13\). Conway spiega il funzionamento del programma con un diagramma, che parte da un intero del tipo generale \(x=5^{n}\cdot 7^{d}\cdot 13\), con \(d \lt n\). Poniamo
Il diagramma è il seguente:
Un numero della forma \(x=5^{n} 7^{d} 13\) con il gruppo di operazioni \((AB)^{d}J\) viene trasformato in in numero della forma \(x=2^{d}3^{d}5^{n-d}11\). Applicando il gruppo di operazioni \((EF)^{d}K\) abbiamo un numero della forma \(x=2^{d}5^{n-d}7^{d} 13\). Eseguendo più volte questi due gruppi di operazioni arriviamo infine ad un numero della forma \(x=2^{qd}5^{r}7^{d} 13\).
Applicando il gruppo di operazioni \((AB)^{r}A\) abbiamo un numero della forma \(x=2^{n}3^{r}7^{d-r-1} 17\). A questo punto si analizza il valore di \(r\), prendendo due rami diversi a seconda che \(r=0\) oppure \(r \gt 0\). Se \(r \gt 0\) si esegue un’altra serie di operazioni arrivando ad un numero della forma \(x=5^{n} 7^{d-1}13\), uguale a quella iniziale, e quindi l’algoritmo continua dalla fase iniziale.
Se invece \(r=0\) allora significa che \(d |n\) e dopo un’altra serie di operazioni si arriva ad un numero della forma \(x=5^{n+1}7^{n}13\), anch’essa simile a quella iniziale.
Il numero \(n\) sarà un numero composto se \(d \gt 1\), mentre sarà un numero primo se \(d=1\). Dal diagramma vediamo quindi che \(2^{n}7^{d-1}=2^{n}\) se \(d=1\); questo è l’unico caso in cui l’algoritmo produce una potenza di \(2\) con esponente primo.
Per generare i numeri primi come esponenti del numero \(2\) partiamo con \(d=n-1\), cioè con un numero della forma \(x=5^{n}7^{n-1}13\). L’algoritmo cerca tutti i divisori di \(n\) a partire da \(n-1\); una volta trovato un divisore ripete la logica cercando i divisori di \(n+1\). Quando \(r=0\) si presenta un numero del tipo \(2^{n}7^{d-1}\); se \(d=1\) allora significa che il numero \(n\) è primo, in quanto \(n\) non ha divisori propri compresi nell’intervallo \( 1 \lt d \lt n\).
Il generatore di Conway è molto interessante e a prima vista sorprendente. Tuttavia è del tutto ineficciente come crivello. Richiede \(19\) passi per calcolare il primo numero primo, esponente del numero \(4=2^{2}\). Per calcolare \(8=2^{3}\) sono necessari \(69\) passi.
10) Numeri primi e triangolo di Pascal
Nel \(1972\) Mann and Shanks hanno dimostrato il seguente teorema:
Teorema 10.1 – Mann-Shanks
Un intero \(n \gt 1\) è primo se e solo se
per tutti gli interi \(m\) tali che \( 0 \le 2m \le n\).
Questo criterio per riconoscere i numeri primi può essere illustrato mediante il triangolo di Pascal scritto in forma rettangolare.
Nelle riga di intestazione i numeri primi sono evidenziati in grassetto.
La riga (R0) contiene il primo elemento del triangolo di Pascal. La riga (R1) contiene i numeri della seconda riga del triangolo di Pascal, spostati a destra di due posizioni. La riga (R2) contiene i numeri della terza riga del triangolo di Pascal, spostati a destra di quattro posizioni, e così via. Nella riga \(Rk\) i numeri divisibili per \(k\) sono evidenziati in grassetto.
I coefficienti binomiali \(\binom{n}{k}\), con \(k=0,1,\cdots,n\) si trovano nell’intervallo fra le colonne \(2n\) e \(3n\) comprese. Ad esempio i coefficienti \(1,3,3,1\) stanno fra la terza e la sesta colonna.
Un numero della riga di intestazione viene evidenziato in grassetto e sottolineatura se tutti i numeri presenti nella colonna sono in grassetto.
Il teorema di Mann-Shanks può essere espresso in questa forma:
Teorema 10.2 – Seconda versione
I numeri primi sono tutti quelli che sono evidenziati in grassetto e sottolineatura nella riga di intestazione.
Dimostrazione
Dimostriamo che la condizione è necessaria.
Se un numero di colonna \(\gt 1\) è primo, allora i coefficienti binomiali presenti sulla colonna sono divisibili dal numero di riga.
Sia \(p\) il numero della colonna e sia \(\binom{n}{m}\) il coefficiente binomiale nella n-esima riga e p-esima colonna. Supponiamo che \(n\) non divide \(\binom{n}{m}\); allora poiché
deve essere \((n,m) \gt 1\). Poiché \(p=2n+m\) si avrebbe \((n,m)|p\), impossibile poiché \(p\) è primo.
Dimostriamo ora che la condizione è sufficiente.
Se il numero della colonna è pari \(c=2m\), allora la prima entrata nella riga \(m\) nella colonna \(c\) è \(\binom{m}{0}=1\) e quindi non è divisibile per \(m\).
Se il numero della colonna è dispari e composto possiamo scrivere \(c= p(2m+1)=2pm + p\). Nella colonna \(c\) è presente il coefficiente binomiale \(\binom{pm}{p}\), il quale non è divisibile per \(pm\).
Per maggiori approfondimenti vedere l’articolo di Mann-Shanks [10].
Conclusione
In questo articolo abbiamo esposto una panoramica delle proprietà e della distribuzione dei numeri primi. Si tratta di una panoramica parziale, che tuttavia dovrebbe essere sufficiente per far apprezzare la bellezza e la complessità dei numeri primi. La profondità di questo mondo è motivo di attrazione per molti matematici, in quanto la complessità del mondo dei numeri rispecchia la profondità dell’Universo. Per capire l’interesse dei matematici per questi argomenti teorici possiamo ricordare l’opinione del grande matematico tedesco Jacobi, in una lettera a Legendre del 2 giugno 1830:
“Il signor Fourier era dell’opinione che lo scopo principale delle matematiche fosse l’utilità pubblica e la spiegazione dei fenomeni naturali; ma un filosofo come lui avrebbe dovuto sapere che lo scopo unico della scienza è l’onore dello spirito umano e che, da questo punto di vista, una questione di teoria dei numeri vale tanto quanto una relativa al sistema del mondo”
In un prossimo articolo vedremo in dettaglio i contributi di Eulero, Legendre e Gauss che per primi hanno intravisto la legge relativa alla distribuzione dei numeri primi, anche se non riuscirono a darne una dimostrazione rigorosa.
Bibliografia
[1]T. Apostol – Introduction to Analytic Number Theory (Springer, 1976)
[2]Hardy, Wright – An Introduction to the Theory of Numbers, V edition (Oxford, 1979)
[3]W. Sierpinski – Elementary Theory of Numbers (North Holland)
[4]Yuri Matiasevich – Hilbert’s 10th Problem (The MIT Press)
[5]B. H. Yandell – The Honors Class: Hilbert’s Problems and Their Solvers (A.K. Peters)
[6]C. F. Gauss – Disquisitiones Arithmeticae (Springer-Verlag, 1985)
[7]T. Cormen, R. Rivest, C. Leiserson, C. Stein – Introduction to Algorithms (The MIT Press)
[8]K. Knopp – Theory and Application of Infinite Series (Dover)
[9] W. LeVecque – Fundamentals of Number Theory (Addison-Wesley)
[10]H. B. Mann, D. Shanks – A necessary and sufficient condition for primality (J. Combin. Theory Ser. A 13 (1972), 131–134)

0 commenti