La nascita della probabilità classica può essere fissata nel secolo XVII, motivata in particolare dall’esigenza di risolvere problemi relativi al gioco d’azzardo. Già nel secolo precedente alcuni studiosi, in particolare Cardano, avevano dato un contributo importante per calcolare le probabilità nei casi più semplici. Tuttavia solo nel secolo successivo Pascal e Fermat, studiando alcuni problemi relativi i giochi d’azzardo, tra i quali il famoso problema della divisione della posta, chiamato anche problema dei punti, introdussero alcuni dei concetti fondamentali della Teoria della probabilità classica. Questo sviluppo fu reso possibile anche grazie ai progressi del Calcolo Combinatorio, che è uno strumento fondamentale per contare il numero dei modi nei quali un particolare evento può verificarsi.
In questo articolo descriveremo brevemente alcuni concetti di calcolo combinatorio e illustreremo le soluzioni di Pascal e Fermat al problema dei punti.
1) Blaise Pascal (1623-1662)
Pascal è una figura eccezionale del secolo XVII, che ha dato importanti contributi in varie discipline: matematica, fisica, calcolo meccanico, filosofia.
A sedici anni scrisse un libro di geometria proiettiva, ‘Trattato sulle coniche’, andato poi purtroppo perso. Scoprì un famoso teorema di geometria, il teorema di Pascal, riguardante le condizioni affinché un esagono sia inscrivibile in una una conica qualsiasi. Per i dettagli vedere Wikipedia.
Si interessò di fisica, studiò in particolare la pressione atmosferica, dimostrando che la pressione diminuisce all’aumentare dell’altitudine.
Pascal può essere considerato inoltre il padre del calcolo effettuato tramite macchine. Infatti progettò la prima macchina calcolatrice, chiamata la pascalina, che è l’antenata dei moderni computer.
Era molto interessato al gioco d’azzardo e questo lo portò ad approfondire i suoi studi sul calcolo delle probabilità.
Oltre ad essere stato un grande matematico, Pascal è stato anche un grande pensatore e filosofo cristiano. Ebbe problemi di salute e questo lo condusse ad approfondire le riflessioni sul senso della vita e della morte. Le sue riflessioni sull’uomo e su Dio sono raccolte nella sua fondamentale opera ‘I Pensieri’, pubblicati per la prima volta nel 1669 [1].
La grandezza intellettuale e morale di Pascal è riassunta molto bene nel libro ‘Il Genio del Cristianesimo’ di Chateaubriand [2].
2) Pierre de Fermat (1601-1665)
Fu consigliere al parlamento e avvocato. Ebbe una grande passione per gli studi matematici, intrattenendo un’intensa corrispondenza con i grandi matematici del tempo: Pascal, Huygens e Cartesio.
Fermat può essere considerato il fondatore della moderna teoria dei numeri. Dimostrò diversi teoremi e propose diverse congetture, in seguito dimostrate da Eulero e altri matematici. La più famosa congettura è l’ultimo teorema di Fermat, il quale afferma che non esistono soluzioni intere per l’equazione seguente
nel caso \(n \gt 2\).
La dimostrazione di tale teorema ha impegnato molti matematici nel corso del tempo ed è stata completata solo nel 1995 da Andrew Wiles.
Fermat ebbe un’intensa corrispondenza con Pascal, insieme al quale gettò le basi del calcolo delle probabilità, sotto la spinta dei problemi del gioco d’azzardo.
3) Il calcolo combinatorio
Riportiamo brevemente alcuni concetti elementari di calcolo combinatorio, una branca strettamente collegata con il calcolo delle probabilità. Il calcolo combinatorio venne utilizzato da Fermat e Pascal per risolvere vari problemi legati al gioco d’azzardo; il primo trattato di calcolo combinatorio può essere considerato il libro di Pascal ‘Traité du triangle arithmétique’, scritto nel 1653.
3.1) Permutazioni, disposizioni e combinazioni semplici
Consideriamo un insieme finito \(X_{n}\) contenente \(n\) elementi. Per semplicità possiamo rappresentare gli elementi con i numeri naturali, cioè \( X_{n}=\{1,2, \cdots ,n \}\).
Definizione 3.1
Una permutazione semplice di \(X_{n}\) è una corrispondenza biunivoca di \(X_{n}\) con se stesso.
Indichiamo con \(P_{n}\) il numero di permutazioni di un insieme finito con \(n\) elementi. Due permutazioni quindi hanno gli stessi elementi, ma disposti in ordine diverso. Ad esempio le permutazioni dell’insieme \(X_{3}\) sono le seguenti:
Nelle permutazioni semplici non si possono ripetere gli elementi. È facile dimostrare che il numero delle permutazioni è dato dalla seguente formula:
\[ P_{n}=n!=n\cdot(n-1)\cdot(n-2) \cdots 2\cdot 1 \]Definizione 3.2
Si dice disposizione semplice di n oggetti a k a k o anche di classe k (con \( k \le n\)) ogni sottoinsieme ordinato di \(k\) oggetti presi dall’insieme \(X_{n}\). Due sottoinsiemi si intendono diversi se differiscono o per un elemento o per l’ordine degli elementi. Il numero di disposizioni di \(n\) oggetti di classe \(k\) viene indicato con \(D_{n,k}\).
Esercizio 3.1
\[ D_{n,k} = \frac{n!}{(n-k)!}=n(n-1)\cdots (n-k+1) \]Definizione 3.3
Le combinazioni di n oggetti presi a k a k, oppure della classe \(k\), sono tutti i gruppi di \(k\) oggetti distinti che si possono formare con gli \(n\) oggetti dati, intendendo due gruppi diversi se differiscono per almeno un elemento.
In definitiva, una combinazione semplice della classe \(k\) è un sottoinsieme di cardinalità \(k\) dell’insieme degli \(n\) oggetti dati. Il numero di tali combinazioni semplici si indica con \(C_{n,k}\), oppure con il simbolo binomiale \( \displaystyle\binom{n}{k}\).
Esercizio 3.2
\[ C_{n,k}=\binom{n}{k}=\frac{D_{n,k}}{k!}=\frac{n(n-1)\cdots (n-k+1)}{k!} \]Esempio 3.1 – Il gioco del lotto
Quante cinquine possono uscire su una ruota nel gioco del Lotto?
L’ordine dei numeri non ha importanza. La risposta è dunque
3.2) Permutazioni, disposizioni e combinazioni composte
Definizione 3.4 – Permutazioni con ripetizioni
Supponiamo di avere \(n\) oggetti non tutti distinti, di cui \(t_{1}\) uguali ad \(x_{1}\), \(t_{2}\) uguali a \(x_{2}\), \(\cdots\), \(t_{k}\) uguali a \(x_{k}\), con \(t_{1}+t_{2}+ \cdots + t_{k}=n\). Allora il numero delle permutazioni distinguibili è:
Definizione 3.5 – Disposizioni con ripetizioni
Dati n oggetti distinti \(a_{1}, \cdots,a_{n}\), si chiamano disposizioni con ripetizione di questi oggetti, della classe \(k\), (k intero positivo), tutti i gruppi di \(k\) oggetti distinti o coincidenti che si possono formare con gli \(n\) oggetti dati. Due gruppi sono considerati identici se hanno gli stessi elementi, lo stesso numero di volte e nello stesso ordine. Indichiamo il numero di disposizioni con ripetizioni con il simbolo \(D_{n,k}^{r}\).
Esercizio 3.3
\[ D_{n,k}^{r}= n^{k} \]Esempio 3.2 – Il gioco del Totocalcio
Quante colonne occorre giocare per essere certi di fare 14?
Ovviamente la risposta è
Definizione 3.6 – Combinazioni con ripetizioni
Dati \(n\) oggetti distinti \(a_{1}, \cdots, a_{n}\), si chiamano combinazioni con ripetizione di questi oggetti, della classe \(k\), tutti i gruppi di \(k\) oggetti distinti o coincidenti che si possono formare con gli \(n\). Due gruppi sono considerati identici se hanno gli stessi elementi, lo stesso numero di volte. Il loro numero si indica con \(C_{n,k}^r\).
Teorema 3.1
\[ C_{n,k}^{r}=\binom{n+k-1}{k} \]Dimostrazione
Possiamo tradurre nel problema equivalente di come disporre \(k\) palline in \(n\) scatole. Supponiamo di avere \(n=5,k=5\). Indichiamo le \(n\) scatole con gli \(n\) spazi compresi fra \(n+1\) barre verticali; indichiamo le palline con il simbolo \(*\):
Con questa rappresentazione abbiamo due palline nella prima scatola, una nella seconda e due nella quinta. Escludendo le barre estremi in generale abbiamo \(n-1\) barre e \(k\) asterischi, che possono apparire in un ordine qualsiasi. Si può quindi dedurre che il numero delle combinazioni con ripetizioni di \(n\) oggetti presi a gruppi di \(k\) è uguale al numero di modi di scegliere \(k\) posti fra gli \(n+k-1\) disponibili.
Per uno studio approfondito del calcolo combinatorio e delle sue applicazioni nel calcolo del probabilità vedere [3] e [4].
4) Il triangolo di Pascal
Come è noto il coefficiente binomiale \(\binom{n}{k}\), dove \(n,k\) sono interi positivi rappresenta il numero delle combinazioni semplici di \(n\) oggetti presi a \(k\) a \(k\); in modo equivalente è il numero dei sottoinsiemi di ordine \(k\) che possono essere costruiti con \(n\) oggetti. Si definisce anche \(\binom{n}{0} = 1\) per \(n \ge 0\) e \(\binom{0}{k}=0\) per \(k \ge 1\). Si possono facilmente dimostrare le seguenti formule:
I coefficienti binomiali hanno un ruolo fondamentale in molti problemi di natura combinatoria. Ricordiamo ad esempio il teorema del binomio di Newton:
\[ (x+y)^n = \sum_{k=0}^{n}\binom{n}{k} x^{k} y^{n-k} \]Esercizio 4.1
Dimostrare le seguenti formule:
Un altro esempio importante è il triangolo di Pascal-Tartaglia:
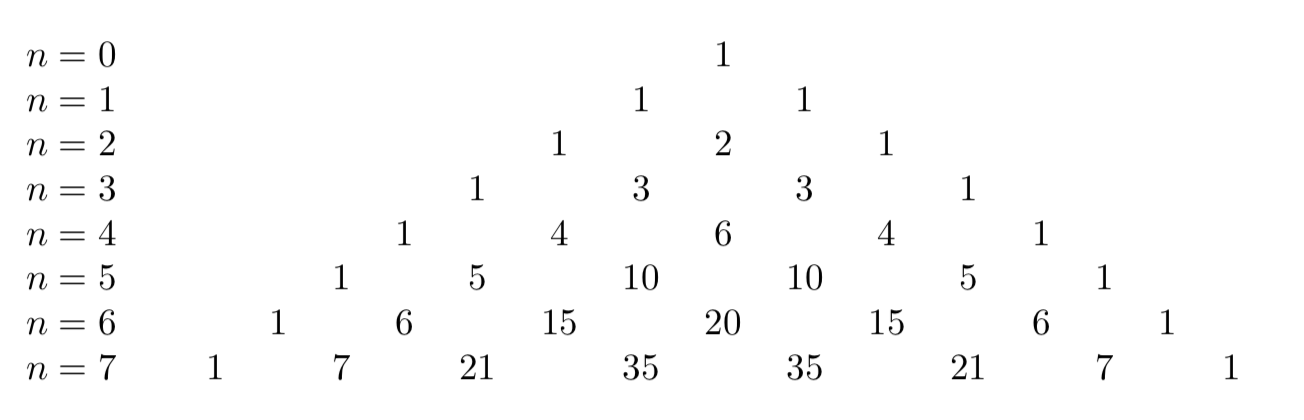
Ogni riga contiene i coefficienti dello sviluppo binomiale di Newton \((a+b)^{n}\). Ad esempio nella riga con n=6 appaiono i coefficienti binomiali \(\binom{6}{k}\), con \(\{k=0,1,2,3,4,5,6 \}\).
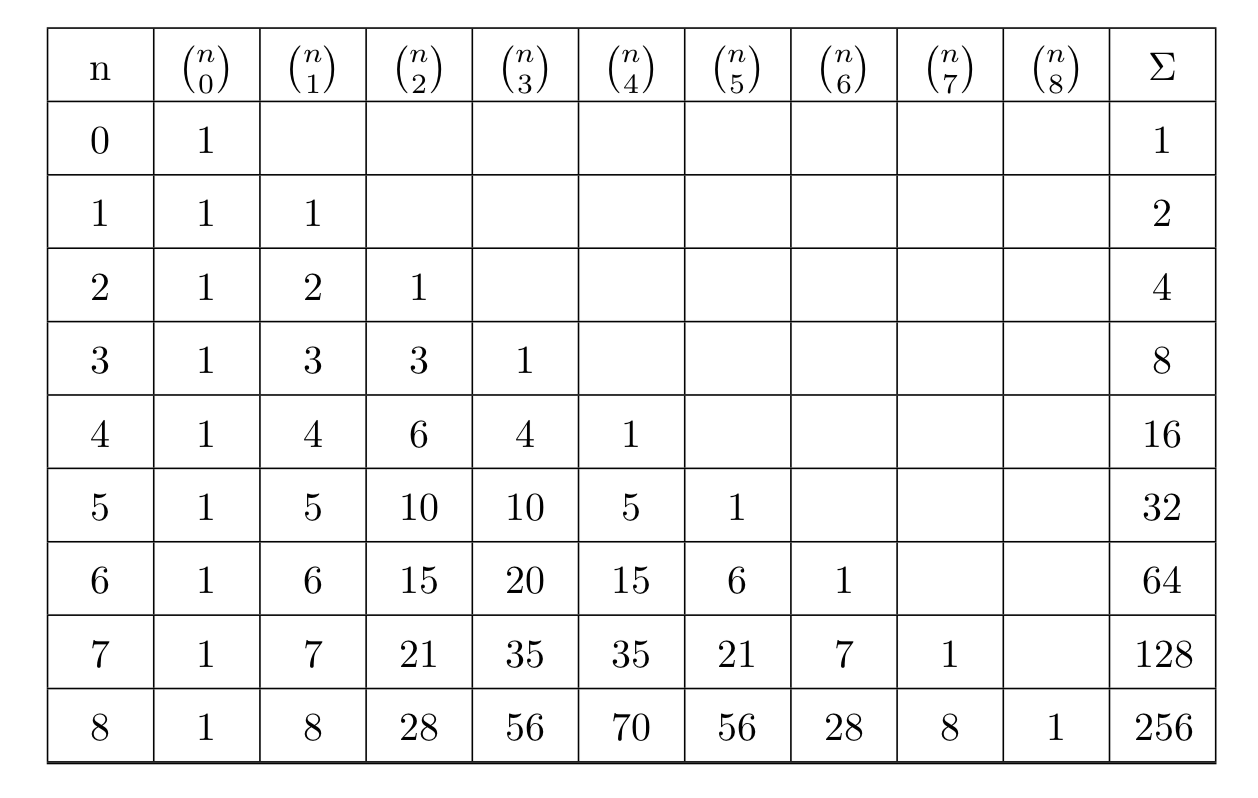
In alcune situazioni è utile rappresentare il triangolo di Pascal in forma tabulare:
Teorema 4.1
\[ \sum\limits_{k=0}^{n}\binom{n}{k}=\sum\limits_{k=0}^{n}\binom{n-1}{k}+ \sum\limits_{k=0}^{n-1}\binom{n-1}{k} \]Teorema 4.2 – Somma per diagonali
\[ \sum\limits_{k=0}^{n}\binom{k}{c}=\binom{n+1}{c+1} \quad c\ge 0 \]Ad esempio, seguendo il triangolo, \(1+3+6+10=20\). Oppure si può usare la rappresentare tabulare, nella quale si somma per colonna. Dimostrare per induzione. Ricordare che \(\binom{k}{c}=0\) se \(k\lt c\).
Esercizio 4.2
\[ \sum\limits_{k=0}^{n}\binom{r+k}{k}=\binom{r+n+1}{n} \]Esercizio 4.3
\[ \frac{1}{2}\binom{2n}{n}+ \binom{2n}{n+1}+ \cdots + \binom{2n}{2n}= 2^{2n-1} \]Per approfondire lo studio del triangolo aritmetico di Pascal vedere [5].
5) Il problema della divisione della posta (o problema dei punti)
Definizione del problema dei punti
Possiamo dare una definizione utilizzando l’esempio di due giocatori che scommettono giocando con una moneta. All’inizio i due giocatori versano una stessa somma che costituisce la posta in gioco.
Il gioco consiste nel lanciare una moneta. In ogni lancio il giocatore A vince un punto se esce testa, altrimenti vince un punto il giocatore B. La posta complessiva viene vinta dal giocatore che avrà totalizzato per primo un numero prefissato \(N\) di punti.
Supponiamo ora che il gioco venga interrotto quando il giocatore A ha totalizzato \(n\) punti e B ha totalizzato \(m\) punti.
Si domanda come deve essere divisa la posta in questa situazione?
Abbiamo visto in un precedente articolo alcune proposte di soluzioni, non corrette, fornite da parte di Pacioli, Tartaglia e Cardano.
Pascal e Fermat hanno dato due soluzioni corrette e distinte, limitandosi al caso in cui i due giocatori hanno la stessa probabilità di vincita di ogni punto (nel nostro esempio supponiamo che la moneta non è truccata).
5.1) Soluzione di Fermat
La strategia seguita da Fermat consiste nel calcolare le probabilità che i due giocatori hanno di vincere, nell’ipotesi che il gioco continui fino alla sua conclusione.
Indichiamo con \(a\) il numero dei punti che mancano al giocatore A per vincere la partita, e in modo simile indichiamo con \(b\) il numero dei punti che mancano al giocatore B.
Possiamo dedurre che il gioco finirà sicuramente dopo \(a+b-1\) ulteriori lanci di monete. Secondo Fermat una divisione equa della posta deve rispettare la proporzione fra i due numeri \(a,b\).
Il metodo di Fermat viene descritto da Pascal con il seguente esempio: supponiamo che al giocatore A mancano \(2\) punti e al giocatore B ne mancano \(3\). Chiaramente il gioco finirà con al massimo altre 4 prove. Sono possibili 16 combinazioni:
\[ \begin{array}{cccc} AAAA & AAAB & AABA & AABB \\ ABAA & ABAB & ABBA & ABBB \\ BAAA & BAAB &BABA & BABB \\ BBAA & BBAB & BBBA & BBBB \\ \end{array} \]Le combinazioni in cui la lettera \(A\) appare almeno due volte comportano la vittoria del giocatore A, le altre del giocatore B. Contando abbiamo \(11\) casi favorevoli ad A e \(5\) a B. Quindi la posta dovrà essere divisa secondo questa proporzione: \(\frac{11}{16}\) al giocatore A e \(\frac{5}{16}\) al giocatore B.
Il metodo di Fermat è diretto e semplice da capire. Tuttavia diventa impraticabile nel caso che di un numero di punti molto grande.
5.2) Soluzione di Pascal
Pascal analizza alcuni casi particolari, ad esempio al giocatore A mancano \(a=b-1\) punti e al giocatore B mancano \(b\) punti. Nei \(a+b-1\) lanci, A vince se ottiene \(a\) punti, poiché anche giocando fino alla fine B otterrà al massimo\(b-1\) punti. Quindi supponendo di effettuare tutte le \(r=a+b-1\) partite A vincerà se escono
\[ a,(a+1), \cdots, (a+b-1) \]teste, mentre B vincerà se escono
\[ 0,1,\cdots, (a-1) \]teste.
Pascal utilizza i coefficienti binomiali e le formule relative al triangolo aritmetico. Indichiamo con \(N_{A},N_{B}\) il numero delle teste necessarie rispettivamente per la vittoria di A e per la vittoria di B. Se facciamo \(r=a+b-1\) lanci, \(k\) teste usciranno \(\binom{a+b-1}{k}\) volte, con la stessa probabilità. È facile verificare che valgono le seguenti formule:
Quindi la divisione della posta, nel caso \(a=b-1\), dovrà essere fatta nella proporzione
\[ A:B = N_{A}:N_{B}=2^{2b-2}+\binom{2b-2}{b-1}:2^{2b-2}-\binom{2b-2}{b-1} \]Vediamo ora il caso generale in cui ad A mancano \(a\) punti e a B mancano \(b\) punti. Poniamo \(r=a+b-1\). Analizziamo la riga di ordine \(r\) del triangolo di Pascal, che contiene i coefficienti dello sviluppo binomiale di \((1+x)^{a+b-1}\). L’ordine di occorrenza delle teste e croci non ha importanza. Supponendo di completare tutte \(r\) partite, il giocatore A vincerà se il numero di teste è \(a,(a+1),(a+2), \cdots ,(a+b-1)\). In caso contrario vincerà il giocatore B. Quindi la divisione della posta tra i due giocatori deve essere fatta con la seguente proporzione:
Teorema 5.1 – Pascal
\[ A:B = \sum\limits_{k=0}^{b-1}\binom{r}{k} :\sum\limits_{k=0}^{a-1}\binom{r}{k} \]Una versione equivalente è data dal seguente teorema:
Teorema 5.1B – Pascal
Con le ipotesi del teorema precedente, il giocatore \(A\) ottiene una frazione della posta uguale a
Dimostrazione
Nella sua dimostrazione Pascal utilizza il metodo di induzione matematica. Il teorema è vero per \(r=1\): in tal caso \(a=b=1\) e ad ognuno dei due giocatori manca un punto, Supponendo vero il teorema quando il numero totale di partite rimaste è \(r=a+b-1\), allora la formula è vera anche se \(r=a+b\). Dopo il nuovo lancio la proporzione attesa per B potrà essere uno dei seguenti valori, a seconda se esce croce o testa:
Poiché i due eventi sono equiprobabili, il valore atteso della proporzione di B prima del lancio è la media aritmetica \(\dfrac{P_{1}+P_{2}}{2}\). Utilizzando le proprietà dei coefficienti binomiali è facile dimostrare che
\[ \frac{P_{1}+P_{2}}{2}= \frac{\sum\limits_{k=0}^{a-1}\binom{a+b-1}{k}}{2^{a+b-1}} \\ \]Con questo il teorema è dimostrato.
Commento sulle soluzioni di Fermat e Pascal
Alcuni autori hanno affermato in passato che la soluzione di Fermat è migliore di quella di Pascal, ritenendo quest’ultima più complicata. A nostro modesto avviso si tratta di un giudizio non condivisibile.
In realtà è vero esattamente il contrario. La soluzione di Fermat richiede che il gioco continui oltre la sua naturale conclusione, per poter calcolare le varie probabilità. Inoltre nel caso di grandi numeri il conteggio diventa molto difficile.
Il procedimento di Pascal rende superfluo contare i casi individuali, come invece richiede il metodo di Fermat. La soluzione di Pascal è molto più elegante: si basa sulle tecniche di condizionamento e ricorsione, che saranno ampiamente utilizzate nei secoli successivi fino ad oggi, in moltissimi tipi problemi .
Inoltre Pascal introduce, anche se non utilizza il nome moderno, il concetto fondamentale di media di una variabile aleatoria, o valore atteso, e pone le basi teoriche per la Teoria della Probabilità.
Pascal oltre a risolvere il problema specifico, ha fornito un metodo potente per risolvere molti altri tipi di problemi, cosa che non si può dire per la soluzione di Fermat.
5.3) Soluzione moderna
Diamo una soluzione moderna, considerando il caso generale in cui la probabilità di vincita del giocatore A sia \(p\) e quella di B sia \(q\), con \(p+q=1\).
Indichiamo con \(E\) l’evento che A vinca la partita se il gioco arriva alla sua conclusione naturale, e \(F_{a,b}\) l’evento che A ha bisogno di \(a\) punti per vincere e B ha bisogno di \(b\) punti. Definiamo la variabile aleatoria
dove \(\chi_{E}\) è la funzione caratteristica dell’evento \(E\) (vale \(1\) se l’evento è vero, altrimenti vale \(0\)). La variabile aleatoria \(X\) indica il guadagno (positivo o negativo) del giocatore A. Abbiamo:
\[ E(X|F_{a,b})= 2 P(E|F_{a,b}) -1 \]Per una divisione equa il giocatore A dovrebbe ricevere una quota \(Q_{a,b}\) della somma totale scommessa pari alla probabilità condizionata di vincere, dato il punteggio raggiunto. Quindi
\[ Q_{a,b}= P(E|F_{a,b}) \]Assumiamo che il gioco continui fino al suo completamento, Devono essere effettuate \( a+b-1\) prove. Il giocatore A vincerà la partita se vince almeno \(a\) di queste prove. Quindi utilizziamo la distribuzione binomiale:
\[ P(E|F_{a,b})= \sum\limits_{k=a}^{a+b-1}\binom{a+b-1}{k}p^{k}q^{a+b-1-k} \]5.4) Approccio alternativo per il problema generale
Consideriamo sempre il problema generale in cui le probabilità di vincita del punto in ogni prova non siano necessariamente uguali. Indichiamo con \(p\) la probabilità che il giocatore A vinca il punto in una prova, e \(q=1-p\) la probabilità che il giocatore B vinca il punto. Indichiamo con p(m,n) la probabilità che A vinca il gioco, dato che A necessita di m punti e B di n. Possiamo scrivere l’equazione alle differenze finite, o equazione di ricorrenza, con le condizioni iniziali:
\[ \begin{array}{l} p(m,n) = p \cdot p(m-1,n) + (1-p)\cdot p(m,n-1) \quad m,n \ge 1 \\ p(m,0)=0; p(0,n)=1 \quad m,n \ge 1 \end{array} \]Procedendo con il metodo di induzione possiamo ricavare le formule dimostrate in precedenza.
6) La scommessa della fede di Pascal
Oltre ad essere un grande matematico, Pascal era anche un filosofo che rifletteva sul significato della vita e sulla grandezza e sulla fragilità dell’uomo. La visione razionalistica di Cartesio non lo soddisfaceva, in quanto non riteneva che la ragione potesse spiegare il mistero dell’uomo e del mondo. Abbracciò con profonda convinzione la fede cristiana, vista come unica possibilità di salvezza.
Per giustificare questa scelta propose anche un argomento probabilistico, la famosa scommessa su Dio. La scommessa è descritta nel suo libro ‘I Pensieri‘ in questo modo:
“Pesons le gain et la perte, en prenant croix que Dieu est. Estimons ces deux cas: si vous gagnez, vous gagnez tout; si vous perdez, vous ne perdez rien. Gagez donc qu’il est, sans hésiter”.
Naturalmente si tratta di una riflessione molto semplice, da prendere soltanto come spinta morale a riflettere sulla fede cristiana. Tuttavia ha un valore anche didattico, come esempio di applicazione della probabilità nella teoria delle decisioni. In condizioni di incertezza si valutano le probabilità degli eventi in gioco e si sceglie la decisione che ha un vantaggio probabile maggiore.
Conclusione
In questo articolo abbiamo visto come Pascal e Fermat partendo da problemi concreti di gioco d’azzardo gettarono le fondamenta del Calcolo delle Probabilità. In un prossimo articolo descriveremo il contributo dato dal matematico olandese Christiaan Huygens (1629–1695), il quale studiò e risolse il problema dei punti in modo indipendente da Pascal e Fermat. Huygens pubblicò nel 1657 un testo in latino ‘De Ratiociniis in Ludo Aleae’ che divenne per diversi anni il testo di riferimento per il Calcolo delle Probabilità.
Bibliografia
[1]B. Pascal – Pensieri (Testo francese a fronte – Bompiani)
[2]Chateaubriand – Génie du christianisme (troisième partie, II, 6)
[3]W. Feller – An Introduction to Probability Theory (Vol. I – Wiley)
[4]D. Knuth – The Art of Computer Programming (Vol. I – Addison-Wesley)
[5]T. Green – Pascal’s Triangle (CreateSpace Independent Publishing Platform)

0 commenti