In questo articolo studieremo alcune proprietà delle serie di Lambert. Quindi, mediante la serie di Lambert relativa alla rappresentazione dei numeri interi come somma di due quadrati, calcoleremo il valore dell’integrale di probabilità di Gauss.
1) Le funzioni generatrici di Dirichlet
Ricordiamo brevemente alcune proprietà delle funzioni generatrici di Dirichlet.
Definizione 1.1
Data una funzione aritmetica \(f(n)\), si chiama funzione generatrice della funzione \(f(n)\) la seguente serie di Dirichlet:
dove \(s=\sigma + it\) è un numero complesso.
Senza entrare in dettaglio sui problemi della convergenza della serie, ricordiamo che per ogni serie di Dirichlet esiste un numero reale \(\sigma_{0}\), chiamato ascissa di convergenza assoluta, tale che la serie converge assolutamente nel semipiano \( \sigma \gt \sigma_{0}\) a destra di \(\sigma_{0}\).
Si può dimostrare che nella regione di convergenza assoluta la serie di Dirichlet rappresenta la funzione aritmetica \(f(n)\) in modo univoco, cioè se due funzioni aritmetiche sono diverse allora anche le rispettive serie di Dirichlet sono diverse.
Esempio 1.1
La serie di Dirichlet più famosa e importante è la funzione zeta di Riemann:
L’ascissa di convergenza della \(\zeta(s)\) è uguale a \(1\).
L’inversa della funzione zeta ha la seguente funzione generatrice di Dirichlet:
\[ \frac{1}{\zeta(s)}=\sum\limits_{n=1}^{\infty}\frac{\mu(n)}{n^{s}} \]dove \(\mu(n)\) è la funzione di Möbius. Ricordiamo che la funzione di Möbius \(\mu(n)\) è così definita:
\[ \mu(n)= \begin{cases} 1 \quad \quad \quad \text{se } n=1 \\ (-1)^{k} \quad \text{se } n=\prod\limits_{i=1}^{k} p_{i} \\ 0 \quad \quad \quad \text{se } n \quad \text{ha un fattore primo quadrato} \end{cases} \]Per la funzione di Möbius vedere l’articolo in questo blog.
Esempio 1.2
Definiamo la seguente funzione aritmetica (chiamata anche carattere di Dirichlet):
Il carattere di Dirichlet quindi assume il valore \(+1\) nei numeri dispari della forma \(4k+1\) e il valore \(-1\) nei numeri dispari della forma \(4k+3\).
La serie di Dirichlet associata è:
\[ L(s)=\sum\limits_{n=1}^{\infty}\frac{\chi(n)}{n^{s}}= 1^{-s}-3^{-s}+5^{-s}- \cdots \]Esercizio 1.1
Dimostrare che la funzione \(\chi(n)\) è completamente moltiplicativa. Cioè per ogni coppia di interi positivi \(n,m\) si ha:
Definizione 1.2
Date due funzioni aritmetiche \( f(n),g(n)\), definiamo il prodotto (o convoluzione) di Dirichlet la seguente funzione aritmetica:
Vale il seguente teorema:
Teorema 1.1
Siano date due funzioni aritmetiche \(f(n),g(n)\) con le rispettive funzioni generatrici di Dirichlet \(F(s),G(s)\). Allora nel semipiano in cui entrambe le serie convergono assolutamente, la funzione generatrice \(H(s)\) della convoluzione \(h=f*g\) è la seguente:
Dimostrazione
Scriviamo il prodotto delle due serie:
Grazie alla convergenza assoluta possiamo moltiplicare e riordinare le due serie come vogliamo, senza cambiare il risultato. Per concludere la dimostrazione basta quindi rappruppare i termini con il prodotto costante \( nm=k\) e scrivere la serie relativa al prodotto.
Dal teorema precedente deriva facilmente il seguente teorema:
Teorema 1.2
Supponiamo che
e \(F(s),G(s)\) siano le funzioni generatrici di Dirichlet di \(f(n),g(n)\). Allora
\[ \begin{array}{l} f(n) = \sum\limits_{d|n}g(d)\mu(\frac{n}{d}) \\ G(s) = \zeta(s) F(s) \end{array} \]Per uno studio approfondito delle serie di Dirichlet vedere un testo di teoria dei numeri, ad esempio [1].
Teorema 1.3
\[ \begin{array}{l} \zeta^{2}(s) = \sum\limits_{n=1}^{\infty}\dfrac{d(n)}{n^{s}} \\ \end{array} \]dove \(d(n)\) è la funzione aritmetica che conta il numero dei divisori di \(n\) (vedi articolo in questo blog).
Suggerimento
Utilizzare il teorema 1.2.
2) Le funzioni generatrici di Lambert
Nonostante l’importanza delle funzioni di Dirichlet, esistono altre funzioni generatrici possibili. Tra queste le serie di Lambert (1728-1777) che hanno la seguente forma:
\[ \sum\limits_{n=1}^{\infty}a_{n}\frac{x^{n}}{1-x^{n}} \]Se la serie \(\sum\limits_{1}^{\infty}a_{n}\) converge, allora la serie di Lambert converge per tutti valori di \(x\), eccetto \(x= \pm 1\). Altrimenti converge per i valori di \(x\) per i quali converge la serie di potenze \(\sum\limits_{n=1}^{\infty}a_{n}x^{n}\).
Nel caso \(a_{n}=1\), se \( |x| \lt 1\) la frazione \(\dfrac{x^{n}}{1-x^{n}}\) è somma di una serie geometrica, e grazie alla convergenza assoluta la serie può essere riordinata senza cambiare la somma.
Teorema 2.1
Se la serie di Lambert converge assolutamente si ha:
dove
\[ b_{n}= \sum\limits_{d|n} a_{d} \]Dimostrazione
La convergenza assoluta permette di riordinare i termini della serie, raggruppando tutti i termini che danno un valore costante \(mn=k\), relativo alla potenza \(x^{k}\). Ad esempio per calcolare il coefficiente di \(x^{6}\), possiamo sommare i coefficienti con tutti i divisori di \(6\): \(a_{1},a_{2},a_{3},a_{6}\). Quindi abbiamo
dove
\[ b_{n}= \sum\limits_{d|n} a_{d} \]Vale il seguente teorema:
Teorema 2.2
Supponiamo che \(A(s),B(s)\) siano le serie di Dirichlet relative ai coefficienti \(a_{n},b_{n}\). Allora:
se e solo se
\[ \zeta(s)A(s)=B(s) \]Esercizio 2.1
\[ \sum\limits_{n=1}^{\infty}\mu(n) \frac{x^{n}}{1-x^{n}}= x \\ \]Esercizio 2.2
\[ \sum\limits_{n=1}^{\infty}d(n)x^{n} = \frac{x}{1-x}+\frac{x^{2}}{1-x^{2}}+\frac{x^{3}}{1-x^{3}}+ \cdots \\ \]Suggerimento
Utilizzare il teorema 1.3 e il teorema 2.1.
Esercizio 2.3
Dimostrare che se
allora
\[ \begin{array}{l} F(x) = \sum\limits_{n=1}^{\infty}G(x^{n}) \\ \end{array} \]3) La funzione aritmetica \(r(n)\)
Definiamo la funzione aritmetica \(r(n)\) come il numero delle rappresentazioni di \(n\) nella forma
\[ n=x^{2}+y^{2} \quad x,y \in \mathbb{Z} \]Si contano come diverse le rappresentazioni che differiscono per i segni o per l’ordine. Ad esempio \(r(5)=8\) in quanto
\[ 5=(\pm 1^{2})+(\pm 2^{2})=(\pm 2^{2})+(\pm 1^{2}) \]Per il numero \(4\) abbiamo
\[ 4=(\pm 0^{2})+(\pm 2^{2})=(\pm 2^{2})+(\pm 0^{2}) \]Nel caso di un numero composto, le condizioni per poter rappresentare un intero come somma di due quadrati sono contenute nel seguente teorema di Fermat:
Teorema 3.1 – Fermat
Sia dato un intero positivo \(n\) con la seguente scomposizione in fattori primi:
dove \(p_{i} \equiv 1 \pmod{4}\) e \(q_{j} \equiv 3 \pmod{4}\). Allora è possibile scrivere \(n=x^{2}+ y^{2}\) se e solo se tutti gli esponenti \(s_{j}\) sono pari.
Per una dimostrazione vedere uno dei testi della bibliografia.
Il seguente teorema è stato dimostrato da Jacobi mediante la sua teoria delle funzioni ellittiche. Tuttavia una forma equivalente era stata dimostrata anche da Gauss nella sua opera fondamentale ‘Disquisitiones Arithmeticae‘, pubblicata nel 1801 in latino.
Teorema 3.2 – Jacobi-Gauss
\[ r(n)=4(d_{1}(n) – d_{3}(n)) \]dove \(d_{1}(n),d_{3}(n)\) sono rispettivamente il numero di divisori di \(n\) della forma \(4n+1\) e \(4n+3\).
Per la dimostrazione vedere [2].
Esempio 3.1
Nel caso \(n=10\) abbiamo \(r(10)=8\). I divisori del tipo \(4k+1\) sono \(1,5\). Non ci sono divisori del tipo \(4k+3\). Quindi
Notiamo che dalla definizione del carattere di Dirichlet risulta:
\[ d_{1}(n)-d_{3}(n)=\sum\limits_{d|n}\chi(d) \]4) La funzione generatrice di \(r(n)\)
Possiamo ora tornare alla nostra funzione \(r(n)\). In base al teorema 3.2 possiamo scrivere
\[ r(n)=4 \sum\limits_{d|n}\chi(d) \]Per il teorema 1.2 abbiamo quindi
\[ \sum\limits_{n=1}^{\infty}\frac{r(n)}{n^{s}}=4\zeta(s)\sum\limits_{n=1}^{\infty}\frac{\chi(n)}{n^{s}} \]Dalla precedente relazione e dal teorema 2.1 deriva facilmente il seguente
Teorema 4.1
\[ \sum\limits_{n=1}^{\infty}r(n)x^{n} = 4 \left(\frac{x}{1-x}-\frac{x^{3}}{1-x^{3}}+\frac{x^{5}}{1-x^{5}}- \cdots \right) \\ \]Consideriamo ora la serie seguente
\[ S= 1+2x+2x^{4}+2x^{9}+\cdots \]Se calcoliamo il quadrato della serie \(S^{2}\), otteniamo una serie di potenze nella quale il coefficiente davanti a \(x^{n}\) è proprio \( r(n)\). Infatti ogni coppia di esponenti \( i,k\) tale che \(i^{2}+k^{2}=n\) contribuisce al coefficiente con un valore unitario. Da questa osservazione possiamo scrivere il teorema precedente in questa forma equivalente:
Teorema 4.2
\[ (1+2x+2x^{4}+2x^{9}+\cdots)^{2}=1+4\left(\frac{x}{1-x}-\frac{x^{3}}{1-x^{3}}+\frac{x^{5}}{1-x^{5}}- \cdots \right) \]Nei paragrafi successivi utilizzeremo questa formula per calcolare l’integrale di Gauss.
5) L’integrale di probabilità di Gauss
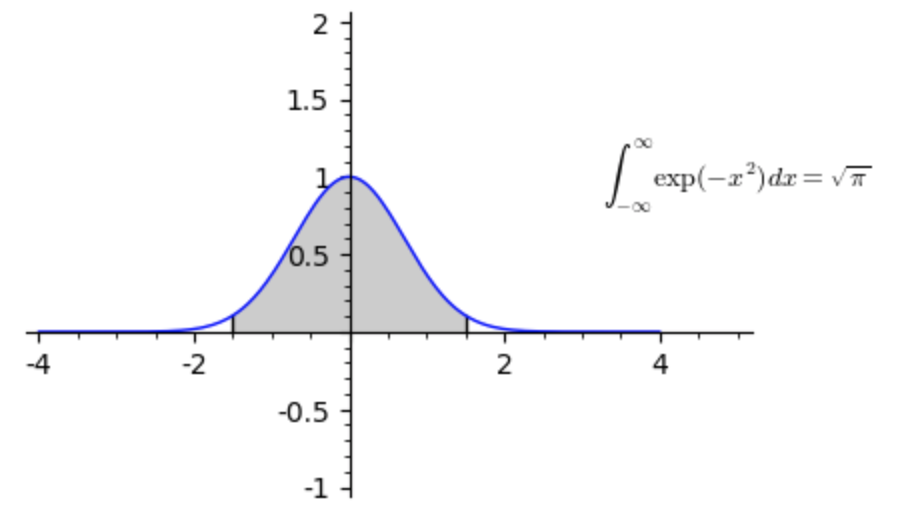
L’integrale di Gauss è l’integrale della funzione \(f(x)=e^{-x^{2}}\) calcolato su tutto l’asse reale:
\[ \begin{array}{l} \int\limits_{- \infty}^{\infty}e^{-x^{2}} dx = \sqrt{\pi} \end{array} \]La funzione \(e^{-x^{2}}\) è simmetrica rispetto all’origine e quindi basta calcolare l’integrale solo sulla semiretta reale positiva:
\[ I= \int\limits_{0}^{\infty}e^{-x^{2}} dx = \frac{\sqrt{\pi}}{2} \\ \]Anche se viene collegato al nome di Gauss, l’integrale era già noto a De Moivre (1667-1754) nei suoi studi sul calcolo delle probabilità, in particolare nel suo libro ‘The Doctrine of Chances‘ del 1718. Era inoltre oggetto di studio da parte di Laplace (1749-1827).
L’integrale di Gauss non è calcolabile con metodi elementari. Uno dei metodi più semplici è probabilmente quello di Poisson (1781-1840) che consiste nel calcolare l’integrale doppio
\[ \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} e^{-(x^{2}+y^{2})}dx dy \]tramite le coordinate polari, e sfruttare il fatto che l’integrale doppio si può esprimere come prodotto dei due integrali parziali. Per i dettagli vedere un testo di analisi matematica.
Supponendo di conoscere il valore dell’integrale di Gauss possiamo dimostrare il seguente teorema:
Teorema 5.1
\[ \alpha = \lim_{x \to 1-0}\sqrt{1-x}(1+x +x^{4}+x^{9}+ \cdots + x^{n^{2}}+ \cdots)=\frac{\sqrt{\pi}}{2} \]Suggerimento
Utilizzare la formula per l’approssimazione dell’integrale della funzione \(f(x)=e^{-x^{2}}\) mediante le somme di Riemann:
Conoscendo il valore dell’integrale di Gauss, possiamo facilmente dedurre che \(\alpha= I=\dfrac{\sqrt{\pi}}{2}\).
6) Calcolo dell’integrale di Gauss mediante la serie di Lambert
Supponiamo ora di non conoscere il valore dell’integrale di Gauss. Se riusciamo a calcolare il limite del teorema precedente in modo alternativo, potremmo calcolare l’integrale di Gauss. In base al teorema 4.2 possiamo scrivere:
\[ \begin{array}{l} \alpha ^{2}= \lim\limits_{x \to 1-0} \left(1-x \right) \left(1+x +x^{4}+x^{9}+ \cdots + x^{n^{2}}+ \cdots \right)^{2} \\ = \dfrac{1}{4}\lim\limits_{x \to 1-0} \left(1-x\right)\left(2+ 2x +2x^{4}+2x^{9}+ \cdots + 2x^{n^{2}}+ \cdots\right)^{2} \\ = \dfrac{1}{4} \lim\limits_{x \to 1-0}\left(1-x \right) \left(1+4\left(\dfrac{x}{1-x}-\dfrac{x^{3}}{1-x^{3}}+\dfrac{x^{5}}{1-x^{5}}- \cdots \right)\right) \\ = \lim\limits_{x \to 1-0}\left(1-x \right) \left(\dfrac{x}{1-x}-\dfrac{x^{3}}{1-x^{3}}+\dfrac{x^{5}}{1-x^{5}}- \cdots \right) \\ \end{array} \]Il passaggio dalla seconda alla terza espressione è facilmente giustificabile. Ricordiamo ora la famosa formula di Leibniz (1646-1716):
\[ 1 -\frac{1}{3}+\frac{1}{5}- \frac{1}{7}+ \cdots = \frac{\pi}{4} \]Utilizzando la formula di Leibniz possiamo completare il calcolo del limite, ottenendo il seguente risultato:
\[ \alpha ^{2}= 1 -\frac{1}{3}+\frac{1}{5}- \frac{1}{7}+ \cdots = \frac{\pi}{4} \]Quindi possiamo concludere che l’integrale di Gauss \(I\) vale:
\[ I = \alpha = \frac{\sqrt{\pi}}{2} \]Conclusione
Abbiamo visto in questo articolo un esempio di come un risultato che appartiene strettamente alla Teoria dei Numeri può essere utilizzato per dimostrare teoremi e proprietà propri dell’Analisi matematica. Questo conferma ancora una volta la profonda unità della Matematica. In articoli successivi studieremo altre proprietà delle serie di Dirichlet e delle serie di Lambert.
Bibliografia
[1]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991)
[2]W. LeVeque – Fundamentals of Number Theory (Dover)
[3]Hardy, Wright – An Introduction to the Theory of Numbers (Oxford University Press)

0 commenti