Il principio dei cassetti viene attribuito al matematico tedesco Dirichlet (1805-1859). Viene anche chiamato principio di Dirichlet o principio della piccionaia (pigeonhole principle).
In questo articolo viene illustrato il principio di Dirichlet e viene fatta una breve introduzione alla teoria di Ramsey, con alcuni esempi di calcolo dei numeri di Ramsey. Per un approfondimento degli argomenti di questo articolo si può vedere [1] (link Amazon.com).
1) Il principio dei cassetti
Teorema 1.1 – Principio base dei cassetti
Un insieme \(X\) di \(n\) elementi viene suddiviso in \(r\) sottoinsiemi disgiunti. Se \(n > r\) allora almeno uno dei sottoinsiemi contiene più di un elemento.
Nonostante sia un principio molto semplice, è utile in molte situazioni per risolvere problemi anche difficili.
Esercizio 1.1
Sia \(X = \{a_{1},a_{2}, \cdots a_{n}\}\) un insieme di n interi. Dimostrare che è sempre possibile scegliere un sottoinsieme di \(X\) tale la somma dei suoi numeri è divisibile per \(n\).
Esercizio 1.2
Dati \(n+1\) interi, dimostrare che se ne possono sempre scegliere due la cui differenza è divisibile per \(n\).
Esercizio 1.3
Sia X un insieme qualunque di \(r\) interi. Se \(n > 1\) e \(2^{r}>n+1\) dimostrare che si possono sempre trovare due sottoinsiemi distinti di \(X\), tali che le somme dei lori interi sono congruenti modulo \(n\), cioè la loro differenza è un multiplo di \(n\).
Suggerimento
Ricordare che dato un insieme di \(r\) interi, il numero totale dei sottoinsiemi non vuoti è \(2^{r}-1\).
La condizione \(2^{r}>n+1\) non può essere abbassata. Se \(2^{r}=n+1\) esiste almeno un insieme per il quale la proprietà non è più vera. Ad esempio \(X=\{1,2,2^{2},2^{3}, \cdots 2^{r-1}\}\).
Esercizio 1.4
Dato un esagono di lato uguale a \(1\). Se ci sono \(7\) punti dentro la superficie dell’esagono, allora esistono almeno due punti la cui distanza è minore od uguale a \(1\).
Esercizio 1.5
Ci sono \(8\) persone sedute in una tavola ottagonale. In ogni posto c’è un cartellino con il nome di una persona (i nomi sono tutti diversi). All’inizio tutte le persone si siedono nel posto sbagliato. Dimostrare che è sempre possibile effettuare una rotazione della tavola in modo che almeno due persone siano nel posto giusto.
Esercizio 1.6
Nel piano cartesiano è definito il reticolo dei punti con coordinate intere (lattice plane). Dimostrare che presi \(5\) punti qualunque del reticolo, il punto intermedio di ameno una coppia fa parte del reticolo. Il punto intermedio è definito facendo la medi aritmetica delle coordinate dei due punti.
2) Il principio dei cassetti generalizzato
Teorema 2.1
Supponiamo di avere un insieme \(X\) di n oggetti, con \(n > mk\). Se l’insieme viene suddiviso in \(k\) sottoinsiemi disgiunti, allora almeno uno dei sottoinsiemi contiene più di \(m\) elementi.
Dimostrazione
Supponiamo \(X = X_{1} \cup X_{2} \cdots \cup X_{k}\). Allora se fosse \(|X_{i}| \le m \quad \forall i: \quad 1 \le i \le k\), si avrebbe: \(n=|X|=\sum_{i=1}^{k}|X_{i}| \le mk\), contrariamente all’ipotesi che \(|X|=n > mk\).
Esercizio 2.1
Dimostrare che in un gruppo di 6 persone, almeno 3 si conoscono fra loro, oppure almeno 3 non si conoscono l’un l’altro.
Dimostrazione
Supponiamo che le \(6\) persone siano sedute ai vertici di un tavolo esagonale. Per ognuna delle 15 coppie tracciamo un segmento e assegniamo un colore: rosso se le persone della coppia si conoscono, blu altrimenti. Dal punto di vista geometrico, si tratta di dimostrare che qualunque sia la colorazione assegnata, è sempre possibile trovare un triangolo di soli lati rossi o di soli lati blu.
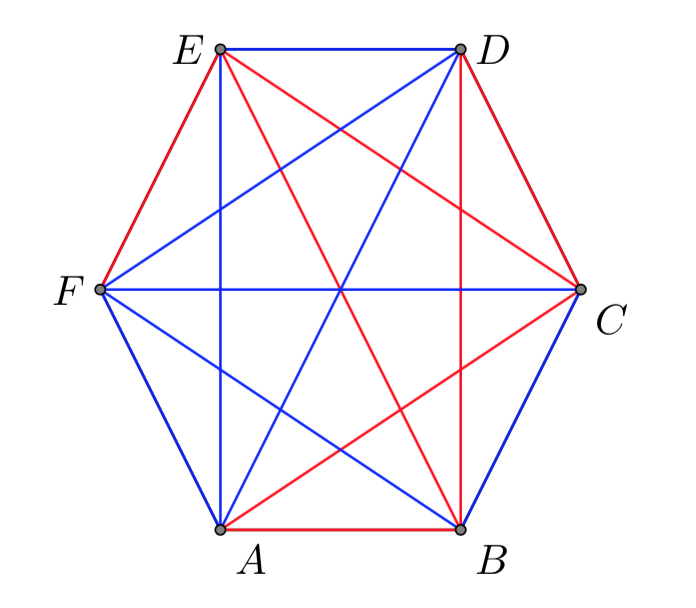
Scegliamo una persona qualsiasi del gruppo, indicandola con P. Rimangono 5 persone; per il principio di Dirichlet sono possibili due casi: P conosce almeno tre persone, oppure P non è conosciuta da almeno tre persone. Supponiamo il primo caso (il secondo si tratta in maniera analoga). Indichiamo le tre persone con A,B,C. Tracciamo i segmenti rossi fra P e A,B,C. Ora se esiste un segmento rosso fra due tra A,B,C abbiamo finito, ad esempio se esiste un segmento fra A e C abbiamo il triangolo rosso ACP. Se invece i segmenti fra A,B,C sono tutti blu allora abbiamo il triangolo blu ABC.
3) La Teoria di Ramsey
La Teoria di Ramsey studia le proprietà che rimangono conservate in una partizione di un dato insieme. Un modo equivalente è quello di dire che se un insieme \(X\) ha una data proprietà \(P\), allora se \(X\) viene decomposto in sottoinsiemi, almeno uno di questi conserva la proprietà \(P\) (“non esiste un disordine completo“).
Per introdurre la teoria di Ramsey è necessario ricordare alcune definizioni sui grafi e sulle colorazioni dei grafi.
3.1) Richiami sui grafi e sulle colorazioni
Definizione 3.1
Un grafo è una coppia ordinata \(G=(V,E)\), dove \(V\) è l’insieme di elementi chiamati vertici o nodi, e \(E\) è costituito da un sottoinsieme del prodotto cartesiano \( V \times V\), cioè un insieme di coppie di vertici. Gli elementi di \(E\) si chiamano archi o cammini (edge in inglese).
Un grafo si dice semplice se non ha cappi, cioè archi che iniziano e terminano sullo stesso vertice, oppure archi multipli tra due vertici. L’ordine di un grafo è il numero dei vertici, cioè degli elementi di \(V\). Il grado di un vertice è il numero degli archi che incidono sul vertice. Due archi si dicono adiacenti se hanno un vertice in comune. Due vertici si dicono adiacenti se esiste un arco che li collega.
Un grafo si dice orientato se le le coppie dei vertici sono ordinate; altrimenti si dice non orientato. In questo articolo consideriamo solo grafi non orientati.
Definizione 3.2
Un grafo non orientato con \(n\) vertici si dice completo, e si indica con \(K_{n}\), se ogni vertice è adiacente a tutti gli altri vertici.
Alcuni esempi sono i seguenti:
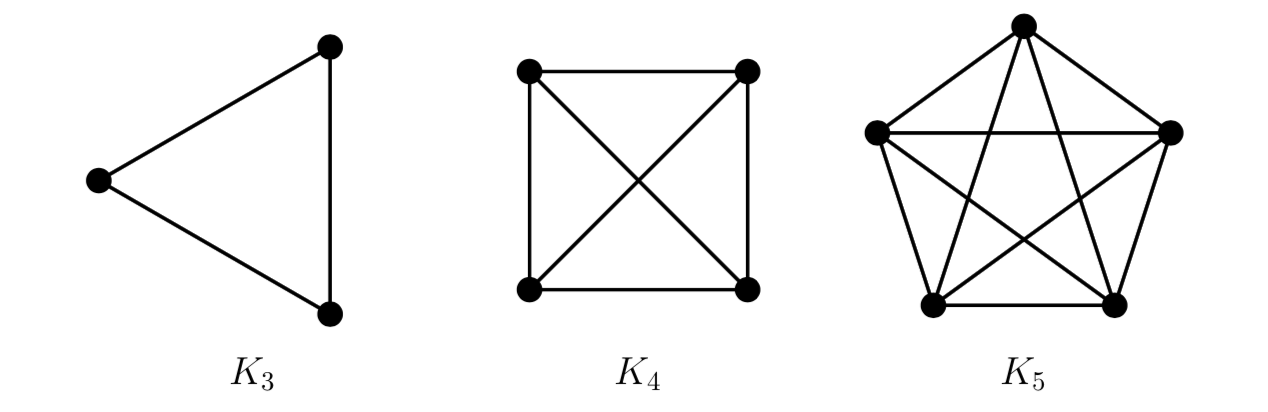
Esercizio 3.1
Dimostrare che il numero degli archi di un grafo completo di ordine \(n\) è
Esercizio 3.2
Dimostrare che in un grafo G non orientato, la somma dei gradi dei vertici è uguale al doppio del numero degli archi. Inoltre il numero dei vertici di grado dispari è pari.
Definizione 3.2
Una r-colorazione dei vertici del grafo \(g(V,E)\) è una funzione \(f: V \to \{1,2, \cdots r\}\). Definizione simile per la r-colorazione degli archi.
4) Il teorema di Ramsey e i numeri di Ramsey
La teoria di Ramsey riguarda in particolare le 2-colorazioni degli archi di un grafo. Per convenzione si utilizzano i colori rosso e blu.
Definizione 4.1
Siano dati due interi positivi \(s,t\). Il numero di Ramsey \(R(s,t)\) è definito come l’ordine del grafo completo più piccolo che, se colorato con due colori rosso e blu, contiene un sottografo completo colorato di rosso \(K_{s}\), oppure un sottografo completo colorato di blu \(K_{t}\).
Teorema 4.1 (Ramsey)
Dati due interi positivi \(s,t\), esiste un intero minimo \(n\), dipendente da \( s,t\) e indicato con \(n=R(s,t)\), tale che ogni 2-colorazione degli archi di un grafo completo \(K_{n}\) di ordine n, contiene un sottografo completo di ordine \(s\), i cui archi sono tutti del colore rosso, oppure contiene un sottografo completo di ordine \(t\), i cui archi sono tutti del colore blu.
Inoltre se \(s,t \ge 2\) allora vale la seguente relazione:
In questo articolo ci limitiamo ad enunciare il teorema base di Ramsey, il quale garantisce l’esistenza del numero \(R(s,t)\) per ogni coppia di interi positivi \(s,t\). In un successivo articolo illustreremo in dettaglio il teorema, alcune sue estensioni ed applicazioni. Per uno studio approfondito della teoria di Ramsey vedere [2] (link Amazon.com).
Esercizio 4.1
Dimostrare le seguenti relazioni:
Esercizio 4.2
Dimostrare che \(R(3,3)=6\). In altre parole dimostrare che per il grafo completo \(K_{6}\) qualunque colorazione degli archi con due colori rosso e blu, contiene almeno un triangolo con lati tutti rossi o tutti blu.
Dimostrare anche che per un grafo \(K_{5}\) si può sempre trovare una colorazione che non contiene alcun triangolo con lati dello stesso colore.
In base all’esercizio 2.1 sappiamo già che \(K(3,3) \le 6\). Rimane da dimostrare che \(K(3,3) >5\). Per questo basta analizzare la seguente colorazione del seguente grafo completo \(K_{5}\).
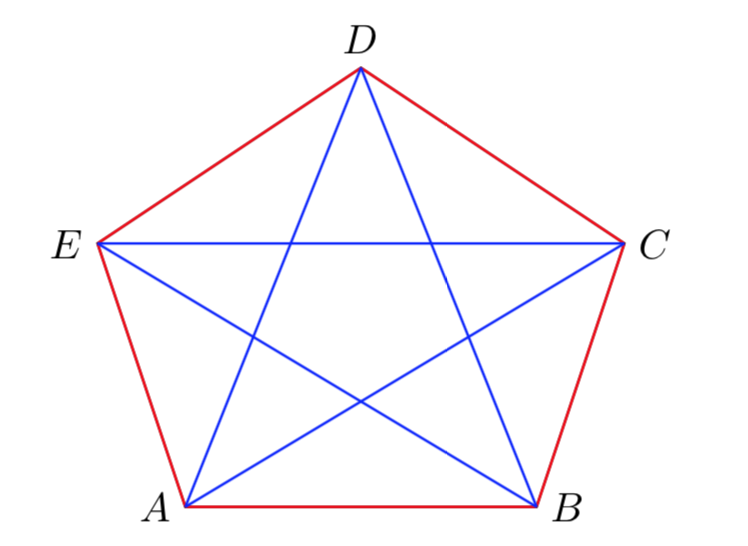
Esercizio 4.3
Dimostrare che ogni colorazione con due colori di un grafo completo \(K_{6}\) contiene almeno due triangoli monocromatici.
Esercizio 4.4
Dimostrare che \(R(3,4)=9\)
Traccia
Dimostriamo intanto che \(R(3,4) > 8\). Per questo basta la seguente figura, la quale illustra un caso di colorazione di un grafo \(K_{8}\) che non contiene un grafo \(K_{3}\) rosso e neanche un \(K_{4}\) blu.
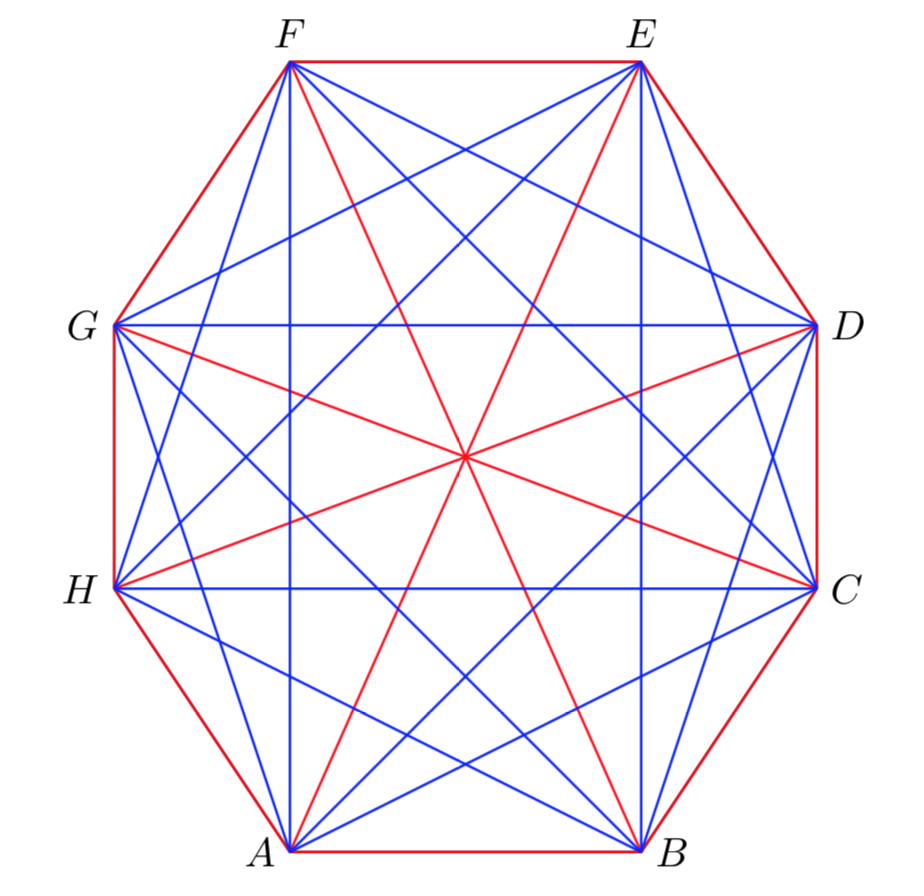
Per dimostrare che \(R(3,4) \le 9\) applicando il teorema di Ramsey, abbiamo: \(R(3,4) \le R(3,3) + R(2,4)=6+4=10\).
Resta da dimostrare che \(R(3,4) <10\). Supponiamo che esista una colorazione rossa e blu di \(K_{9}\) tale che non ci sia nessun sottografo rosso \(K_{3}\) e nessun sottografo blu \(K_{4}\). Allora ogni vertice del grafo deve essere incidente a 3 archi rossi e 5 archi blu, altrimenti sarebbe possibile costruire un \(K_{3}\) rosso, oppure un \(K_{4}\) blu, contrariamente all’ipotesi. Consideriamo ora soltanto il sottografo rosso, che ha \(9\) vertici, ognuno con tre archi incidenti; la somma dei gradi di tutti i vertici è quindi 3*9=27. Questo non è possibile in quanto la somma dei gradi di un grafo non orientato deve essere pari (vedi Esercizio 3.2). Quindi l’ipotesi iniziale è errata e possiamo concludere che \(R(3,4)=9\).
5) Calcolo dei numeri di Ramsey
I valori dei numeri di Ramsey sono molto difficili da calcolare. Alcuni dei numeri calcolati sono presentati nella tabella seguente:
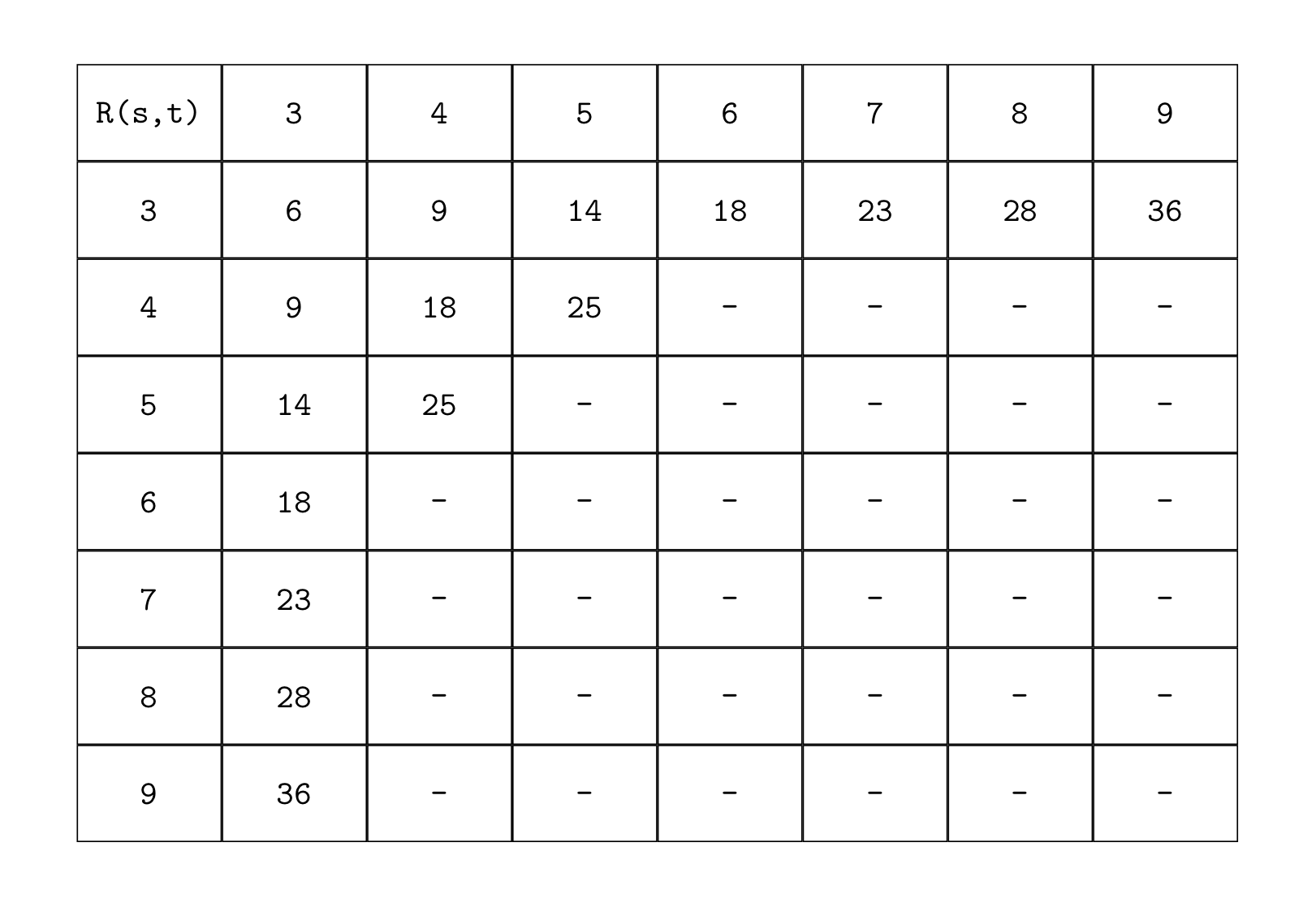
Conclusione
La teoria di Ramsey trova applicazioni interessanti in diversi settori, tra i quali la Teoria dei numeri, l’Algebra, la Teoria dell’informazione. In un prossimo articolo descriveremo con maggiore dettaglio la teoria di Ramsey, con particolare riguardo alle applicazioni alla teoria dei numeri.
Bibliografia
[1]M. Erickson – Introduction to Combinatorics (Wiley)
[2]Graham, Rothschild, Spencer – Ramsey Theory (Wiley)

0 commenti