Il Principio di Inclusione-Esclusione

Il principio di inclusione-esclusione è un risultato importante del calcolo combinatorio che trova applicazioni in vari campi, dalla teoria dei numeri, al calcolo delle probabilità, alla teoria della misura. In questo breve articolo vengono esposte diverse formulazioni del principio, seguite da alcune applicazioni ed esercizi.
Per un approfondimento vedere ad esempio ^[1] e ^[2].

---

1) Il principio di inclusione-esclusione

Siano dati n insiemi di cardinalità finita \(S_{1}, S_{2}, \cdots S_{n}\). Indichiamo con \(S\) l’unione degli \(n\) insiemi, cioè \(S = S_{1} \cup S_{2} \cup \cdots \cup S_{n}\). Spesso è necessario calcolare la cardinalità dell’insieme \(S\), cioè il numero degli elementi distinti di \(S\). Il principio di esclusione, espresso nel seguente teorema, permette di effettuare questo calcolo in modo semplice.

Teorema 1.1
La cardinalità dell’insieme unione \(S\) è data da

\[ |S| =\sum_{k=1}^{n} (-1)^{k+1} \cdot C(k) \]

dove \(C(k) = | {S_{i_{1}}} \cap \cdots \cap S_{i_{k}}| \quad con \quad 1 \le i_{1} < \cdots < i_{k} \le n\) .

Espandendo l’espressione compatta del teorema abbiamo:

\(\\|S_{1} \cup \cdots \cup S_{n}|  =    \\ |S_{1}| + |S_{2}| + \cdots |S_{n}| – |S_{1} \cap S_{2}| – \cdots -|S_{n-1} \cap S_{n}|   \\  +|S_{1} \cap S_{2} \cap S_{3}| + \cdots + |S_{n-2} \cap S_{n-1} \cap S_{n}|  \\   \vdots   \\ + (-1)^{n-1} |S_{1} \cap S_{2} \cdots \cap S_{n}|\\ \)

Il teorema è una estensione al caso generale della proprietà ovvia nel caso di due insiemi \(A,B\). Per calcolare la cardinalità dell’insieme unione \(A \cup B\) bisogna sommare la cardinalità dei singoli insiemi, ma poi bisogna sottrarre il numero degli elementi comuni, cioè appartenenti all’insieme intersezione. In simboli:

\[ |A \cup B| = |A| + |B| – |A \cap B| \]

Nel caso di tre insiemi \(A,B,C\) abbiamo:

\[ \begin{split} |A \cup B \cup C| &=|A| + |B| + |C| \\ & – |A \cap B| – |A \cap C| – |B \cap C| \\ & + |A \cap B \cap C| \end{split} \]

Il seguente grafico illustra la situazione nel caso di tre insiemi: 

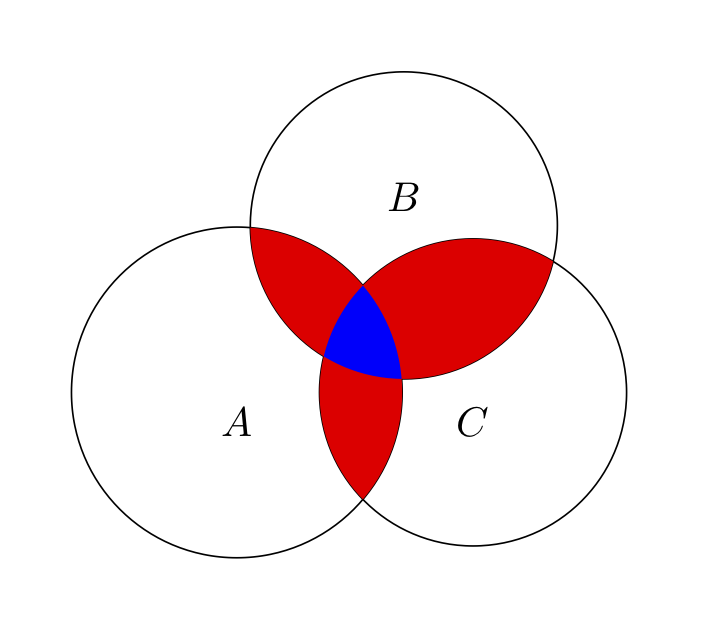
Una formulazione equivalente del principio di inclusione-esclusione è la seguente:

Teorema 1.2
Sia S un insieme di \(N\) elementi e siano \(S_{1},S_{2}, \cdots S_{r}\) sottoinsiemi arbitrari di \(S\) contenenti rispettivamente \(N_{1},N_{2}, \cdots N_{r}\) elementi. Per \(1 \le i < j < l \le r\), sia \(S_{ij…l}\) l’insieme intersezione di \(S_{i},S_{j}, \cdots S_{l}\) e sia \(N_{ij..l}\) numero degli elementi di \(S_{ij \cdots l}\).
Allora il numero degli elementi di S che non appartengono a nessuno degli \(S_{1}, \cdots S_{r}\) è

\[ T = N – \sum_{\substack{1 \le i \le r}}N_{i} + \sum_{\substack{1 \le i < j \le r }}N_{ij} – \cdots + (-1)^{r} N_{12 \cdots r} \]

Dimostrazione
Indichiamo con \(s\) un generico elemento di \(S\) che appartiene ad esattamente \(m\) degli insiemi \(S_{1},S_{2}, \cdots S_{r}\). Se \(m=0\) allora s viene contato esattamente una volta nella formula, precisamente nel primo termine \(N\). Se \(0 < m \le r\), allora s è contato una volta in \(N\), è contato \(\binom{m}{1}\) volte nei termini \(N_{i}\), \(\binom{m}{2}\) nei termini \(N_{ij}\), ecc. Quindi, poiché \(\binom{m}{0}=1\), il contributo al totale T è:

\[ \binom{m}{0} – \binom{m}{1} + \binom{m}{2} – \cdots + (-1)^{m}\binom{m}{m}= (1-1)^{m}=0 \]

per il teorema binomiale di Newton.

Si può dare un terzo enunciato equivalente in termini di probabilità. Al posto degli insiemi abbiamo gli eventi, che non sono altro che insiemi di risultati possibili.

Teorema 1.3
Siano dati n eventi \(E_{1}, E_{2}, \cdots E_{n}\). Allora la probabilità che si verifichi almeno uno degli n eventi è:

\[ \begin{split} P\{E_{1} \cup E_{2} \cdots E_{n}\} = \sum_{1 \le i \le n} P\{E_{i}\} – \sum_{1\le i_{1} < i_{2} \le n}P\{E_{i_{1}} \cap E_{i_{2}}\} + \\ \sum_{1\le i_{1} < i_{2} < i_{3} \le n} P\{E_{i_{1}} \cap E_{i_{2}} \cap E_{i_{3}}\} \cdots + (-1)^{n+1}P\{E_{1}\cap E_{2}\cap \cdots \cap E_{n}\} \end{split} \]

Esercizio
Un dado viene lanciato n volte. Determinare la probabilità che appaiano tutte le 6 facce.

Vediamo ora alcune applicazioni del principio di inclusione-esclusione.

---

2) Il polinomio cromatico di un grafo

Un grafo G consiste in una coppia di insiemi (V,E), dove V è un insieme di nodi o vertici, e E è un insieme di archi o lati (edge), ogni arco essendo definito da una coppia di vertici. Un grafo si dice semplice se non ha archi multipli fra due vertici e non ha cappi(loop). Un grafo si dice connesso se, per ogni coppia di vertici (u, v) ∈ V, esiste un cammino che li collega. Un grafo non connesso è costituito da un numero finito di componenti connesse.
Dato un insieme Q di colori, una colorazione di un grafo è una assegnazione di colori ad ognuno dei vertici. La colorazione si dice propria se in ogni lato i colori dei due vertici sono diversi.

Teorema 2.1
Per ogni grafo \(G = (V, E)\), è possibile definire un polinomio \(P(x)\) tale che per ogni numero naturale \(q\), \(P(q)\) rappresenta il numero di colorazioni proprie del grafo \(G\) con \(q\) colori.

Dimostrazione
Indichiamo con X l’insieme di tutte le colorazioni, proprie e non. Allora si ha \(|X| = q^{n}\), dove \(n\) è il numero dei veritci.
Per ogni lato \(l\) del grafo, indichiamo con \(A_{l}\) l’insieme delle colorazioni possibili per le quali i vertici del lato \(l\) hanno lo stesso colore. Le colorazioni proprie sono quelle che non sono contenute in nessuno degli insiemi \(A_{l}\).
Dato un insieme \(I \subseteq E\), contiamo le colorazioni contenute in \(A_{I}\). Se consideriamo il grafo (V,I), allora una colorazione in \(A_{I}\) assegna lo stesso colore a tutti i vertici nella stessa componente connessa del grafo; quindi se il numero delle componente connesse è \(c(I)\), abbiamo \(|A_{I}|=q^{c(I)}\).
Applichiamo ora il principio di inclusione-esclusione; il numero delle colorazioni proprie è

\[ P_{X}(q)= \sum_{\substack{ I \subseteq E }} (-1)^{|I|} q^{c(I)} \]

Si tratta di un polinomio nella variabile \(q\); il termine principale vale \(q^n\), e deriva dal caso \(I = \emptyset\), cioè se \(I\) è l’insieme vuoto.

Il polinomio \(P_{X}\) viene chiamato polinomio cromatico del grafo G=(V,E).

Esercizio
Calcolare il polinomio cromatico nei seguenti casi:

---

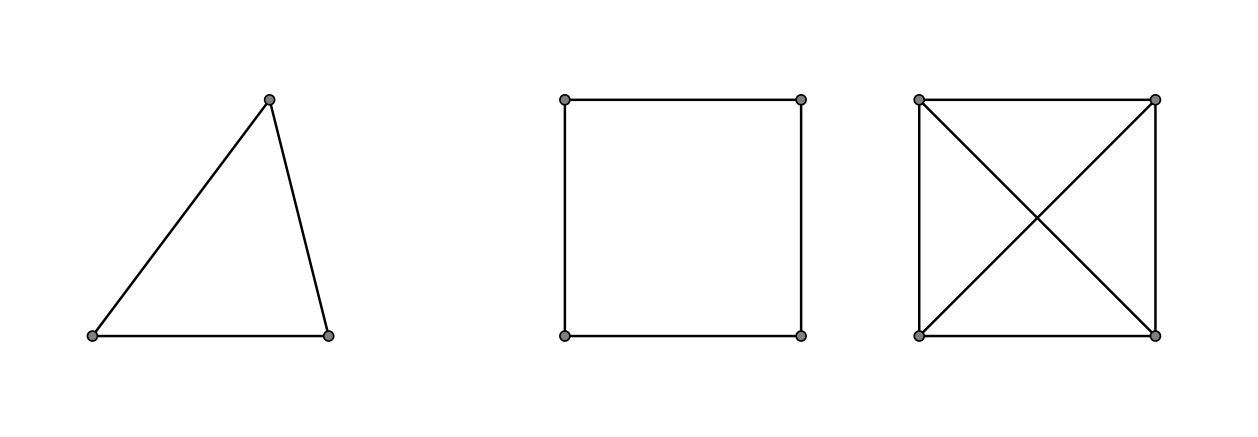
3) Calcolo del numero di funzioni suriettive

Dato un insieme \(A\) di \(m\) elementi, e un insieme \(B\) di \(n\) elementi. È evidente che il numero totale delle funzioni tra A e B è uguale a \(n^{m}\).
Una funzione \(f:A \rightarrow B\) si dice suriettiva se:

\[ \forall {b} \in B \quad \exists a \in A : f(a)=b \]

Esercizio
Determinare il numero totale delle funzioni suriettive fra gli insiemi A, B, se \(m \ge n\).

Suggerimento
Applicare il principio di inclusione-esclusione, escludendo dal totale delle funzioni \(n^{m}\) quelle che assumono un numero di valori diversi inferiore ad \(n\).

---

4) Altri esercizi proposti

Esercizio 4.1
Calcolare il numero di soluzioni della equazione \(x+y+z=15\), dove \(x,y,z\) sono interi non negativi, con la condizione che \(z \le 3\).

Esercizio 4.2
Dato il numero 165, determinare il numero degli interi da 1 a 165 che hanno divisori comuni non banali (diversi da 1) con 165.

Esercizio 4.3
Quanti sono gli interi positivi minori di \(1000\) che non sono divisibili per \(5\) e neanche per \(11\)?

Esercizio 4.4
In un gruppo di 100 persone 70 posseggono una Mercedes e 50 una Fiat. Cosa si può dire sul numero di persone che possiedono sia una Mercedes sia una Fiat?

---

Bibliografia

^[1]William Feller – An introduction to Probability Theory and its applications, Vol. I (Wiley)

^[2]Lipschutz – Theory and problems of Discrete Mathematics (McGraw-Hill)