Problema 1
Calcolare il massimo numero di parti nelle quali un piano può essere diviso da \(n\) rette.
Questo problema è equivalente al problema del massimo numero di parti di una pizza che è possibile fare effettuando n tagli.
Problema 2
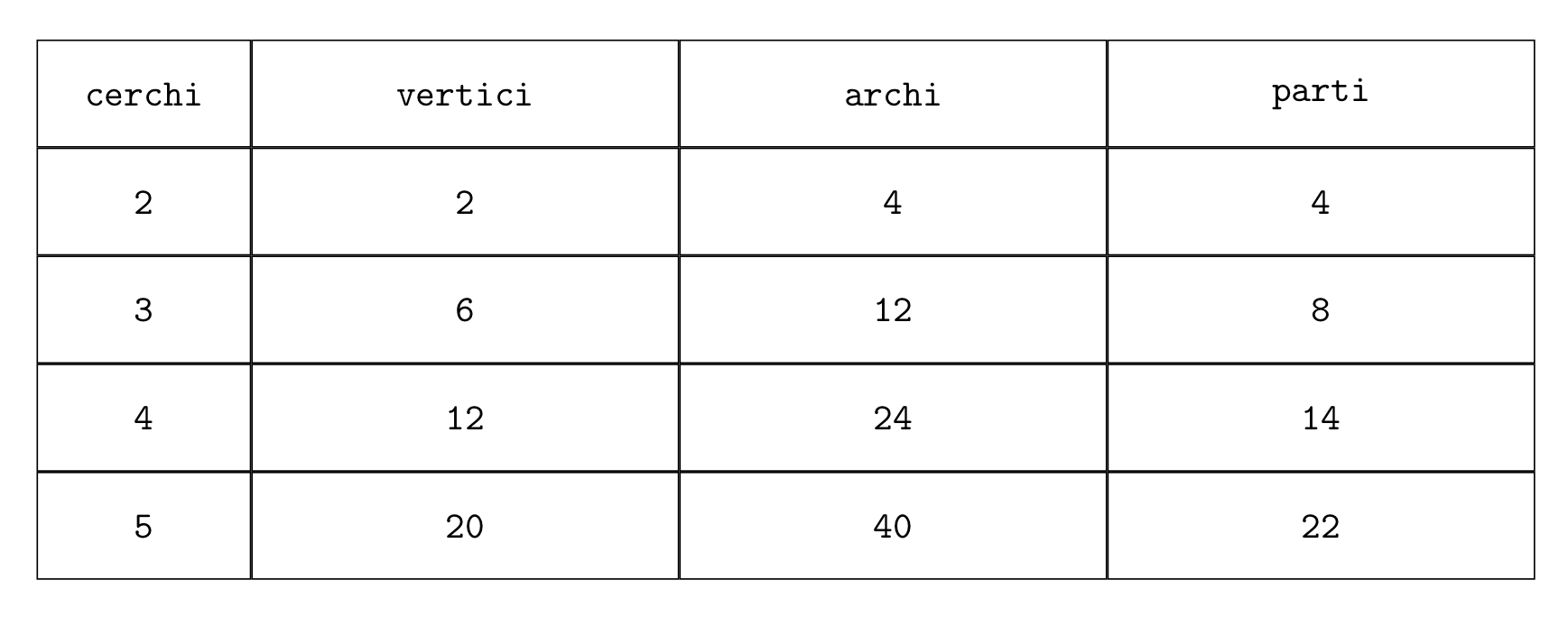
Calcolare il massimo numero di parti nelle quali un piano può essere diviso da \(n\) cerchi.
I due problemi precedenti possono essere generalizzati nello spazio euclideo tridimensionale.
Problema 3
Calcolare il numero massimo di regioni in cui lo spazio tridimensionale può essere diviso da \(n\) piani.
Problema 4
Calcolare il numero massimo di regioni in cui lo spazio tridimensionale può essere diviso da \(n\) sfere.
Per un approfondimento del problema di Steiner vedere ad esempio [3] e [4].
Bibliografia
[1]M. Spiegel – Differenze finite e equazioni alle differenze (Etas Libri)
[2]Tucker – Applied Combinatorics (Wiley)
[3]Knuth, Graham – Concrete Mathematics (Addison Wesley)
[4]Comtet – Advanced Combinatorics (D. Reidel)

4 commenti
Massimiliano Rizzato · 18 Marzo 2022 alle 12:28 AM
Salve,
So che le soluzioni a cui si giunge sono corrette, ma mi sfuggono alcuni passaggi.
Per esempio, nel primo problema, come mai si prende un polinomio di secondo grado per il metodo dei dei coefficienti indeterminati, se si hanno solo i termini per Rn ed Rn-1? Il polinomio caratteristico non è in questo caso di grado 1? Lo stesso vale per il secondo problema.
Potrebbe per favore fornire il calcolo completo per almeno uno dei problemi?
gameludere · 30 Marzo 2022 alle 4:24 PM
Ciao Massimiliano, scusa per la risposta tardiva.
Per risolvere un’equazione lineare alle differenze finite, chiamata anche equazione di ricorrenza, bisogna prima trovare la soluzione generale dell’equazione omogenea, e poi trovare una soluzione particolare dell’equazione non omogenea.
Consideriamo l’equazione di primo grado \(R_{n}-R_{n-1}=n\). L’equazione caratteristica dell’equazione omogenea \(R_{n}-R_{n-1}=0\) è \(\lambda -1=0\), quindi la soluzione generale dell’equazione omogenea è \(R_{n}=k\), dove \(k\) è una costante arbitraria. Per determinare una soluzione particolare dell’equazione non omogenea, possiamo provare con un polinomio di grado maggiore od uguale al grado del polinomio termine noto. Il grado del polinomio di prova dipende dal grado del polinomio termine noto e non dal grado dell’equazione.
Se proviamo con un polinomio di primo grado otteniamo nuovamente la soluzione costante dell’equazione omogenea. Quindi proviamo con un polinomio di secondo grado: \(p(n)=an^{2}+bn+c\). Sostituendo nell’equazione abbiamo:
\[
an^{2}+bn+c – a(n-1)^{2}-b(n-1) -c = n
\]
Svolgendo i calcoli troviamo la soluzione particolare:
\[
-a + 2an + b = n \implies a=b=\frac{1}{2}, c=0 \implies p(n)= \frac{n^{2}+n}{2}
\]
La soluzione generale dell’equazione non omogenea è quindi la somma della soluzione generale dell’equazione omogenea e della soluzione particolare:
\[
R_{n}= \frac{n^{2}+n}{2} + k
\]
Per determinare il valore della costante \(k\) utilizziamo la condizione iniziale \(R_{2}=4\).
Massimiliano Rizzato · 30 Marzo 2022 alle 5:41 PM
Ciao,
Nel frattempo avevo risolto da solo (approfondendo le equazioni alle differenze finite), infatti ho risolto in dettaglio anche tutti gli altri esempi. ,
Quanto mi scrivi conferma esattamente i miei risultati, cosa di cui ti ringrazio molto!
Ciao,
Massimiliano
gameludere · 30 Marzo 2022 alle 9:29 PM
Di nulla, grazie a te per il commento.