Il numero \( \pi \) occupa un ruolo centrale nella Matematica da oltre 2500 anni. Il suo valore è approssimativamente uguale a 3,14. Nella geometria euclidea è definito come il rapporto fra la lunghezza della circonferenza e il diametro di un cerchio. Come è noto nella geometria euclidea tale rapporto è sempre lo stesso, indipendentemente dal raggio del cerchio, mentre questo non è vero nelle geometrie non euclidee.
Il matematico Lambert (1728-1777) ha dimostrato nel 1761 che si tratta di un numero irrazionale, contenente quindi infinite cifre decimali non periodiche.
Nel 1882 il matematico tedesco Lindemann (1852-1939) ha dimostrato che \( \pi \) è un numero trascendente, cioè non è radice di nessun polinomio con coefficienti interi. Questa scoperta fondamentale dimostrò anche che il problema millenario della quadratura del cerchio non ha soluzione. Cioè non è possibile costruire un quadrato con area uguale a quella di un cerchio, utilizzando soltanto riga e compasso.
Il calcolo del valore esatto ha rappresentato una sfida a partire dai Babilonesi, per proseguire con i Greci fino ai nostri giorni, caratterizzati da computer molto potenti che possono calcolare milioni di cifre.
La prima stima fatta nell’antichità è che si tratta di un numero compreso fra 3 e 4. Archimede utilizzò il metodo del calcolo del perimetro dei poligoni inscritti e circoscritti e trovò una prima approssimazione 3,14, vicina al valore del numero razionale \( \displaystyle \frac{223}{71} \).
In questo articolo studieremo alcuni prodotti infiniti nei quali è presente il numero \( \pi \). In successivi articoli studieremo altre rappresentazioni del numero \( \pi \) e gli algoritmi utilizzati per il calcolo delle sue cifre.
1) I prodotti infiniti
Definizione 1.1
Data una successione di numeri reali \( u_{0}, u_{1}, \cdots \) non nulli, definiamo il prodotto parziale di ordine n: \( \prod\limits_{i=0}^{n} u_{i}=u_{0}u_{1} \cdots u_{n} \). Se tale prodotto parziale tende ad un valore finito diverso da zero, questo limite è il valore del prodotto infinito
e il prodotto infinito si dice convergente. Se il limite vale zero allora si dice che il prodotto infinito diverge a zero. Se non converge ad un limite definito, il prodotto infinito si dice oscillante.
In alcuni problemi è conveniente cambiare notazione e scrivere \( u_{n}=1+a_{n} \). Con questa notazione la definizione diventa:
Esercizio 1.1
Dimostrare che una condizione necessaria affinché il prodotto infinito sia convergente è che risulti \( \lim\limits_{n \to \infty}a_{n}=0 \).
Esercizio 1.2
Studiare i seguenti prodotti infiniti:
Riportiamo alcuni teoremi che permettono di stabilire la convergenza dei prodotti infiniti mediante lo studio di serie infinite:
Teorema 1.1
Se tutti i coefficienti soddisfano la condizione \( a_{n} > -1 \), allora condizione necessaria e sufficiente affinché il prodotto infinito sia convergente è che converga la serie logaritmica associata
Teorema 1.2
Un prodotto infinito \( \prod\limits_{n=1}^{\infty}(1+a_{n}) \) con i termini \( a_{n} \) non negativi converge se e solo se converge la serie \( \sum\limits_{n=1}^{\infty}a_{n} \).
Teorema 1.3
Se la serie \( \sum\limits_{n=1}^{\infty}a_{n}^{2} \) converge, allora la serie \( \sum\limits_{n=1}^{\infty}a_{n} \) e il prodotto infinito \( \prod\limits_{n=1}^{\infty}(1+a_{n}) \) convergono entrambi o divergono entrambi.
Teorema 1.4
Un prodotto infinito \( \prod\limits_{n=1}^{\infty}(1-a_{n}) \) con \( 0 \le a_{n} <1 \), converge se e solo se converge la serie \( \sum\limits_{n=1}^{\infty}a_{n} \).
Esercizio 1.3
Dimostrare che il seguente prodotto infinito diverge all’infinito:
Esercizio 1.4
Dimostrare che il prodotto armonico
diverge a zero.
Esercizio 1.5
Dimostrare la seguente formula:
Esercizio 1.6
Dimostrare la seguente formula:
Esercizio 1.7
Dimostrare che il seguente prodotto infinito
converge per \( t>1 \) e diverge per \( t \le 1 \).
Esercizio 1.8
\[ \prod\limits_{n=1}^{\infty}\left(1+\frac{(-1)^{n+1}}{n}\right)=1 \\ \]Lo studio dei prodotti infiniti è un argomento molto vasto ed fondamentale in Analisi Matematica, come quello delle serie infinite. L’estensione della definizione di prodotto infinito al campo dei numeri complessi ha portato a risultati importanti in vari settori, in particolare nello studio della funzione zeta di Riemann, che ha un ruolo centrale nella Teoria dei Numeri.
Per un approfondimento vedere ad esempio il libro di Apostol edito da Pearson[1], oppure il libretto di Knopp[2].
2) La formula di Viète
Una prima rappresentazione del numero \( \pi \) tramite un prodotto infinito è stata proposta da F. Viète (1540-1603):
\[ \frac{2}{\pi} = \sqrt{\frac{1}{2}}\sqrt{\frac{1}{2}+ \frac{1}{2}\sqrt{\frac{1}{2}}}\sqrt{\frac{1}{2}+ \frac{1}{2}\sqrt{\frac{1}{2}+ \frac{1}{2}\sqrt{\frac{1}{2}}}}\cdots \\ \]Per chiarire meglio la formula poniamo
\[ \begin{array}{ll} a_{1} &= \sqrt {\frac{1}{2}} \\ a_{n} &= \sqrt{\frac{1+a_{n-1}}{2}}\\ \end{array} \\ \]La formula di Viète può quindi essere scritta in questo modo più semplice:
\[ \frac{2}{\pi}=\lim\limits_{n \to \infty}(a_{1}a_{2} \cdots a_{n}) \\ \]La formula di Viète è un caso particolare del seguente teorema:
Teorema 2.1 – Eulero
\[ \frac{\sin x}{x}= \prod\limits_{k=1}^{\infty}\cos \frac{x}{2^{k}} \\ \]Dimostrazione
Utilizziamo la nota formula trigonometrica \( \sin 2x= 2 \sin x \cos x \). Iterando questa formula abbiamo:
Utilizzando il limite notevole \( \lim\limits_{x \to 0}\frac{\sin x}{x}=1 \), possiamo subito dedurre che
\[ \lim\limits_{n \to \infty}2^{n} \sin \frac{x}{2^{n}}=x \\ \]Da questo deriva il teorema. La formula di Viète si ottiene ponendo \(x=\frac{\pi}{2} \).
Presentiamo anche la dimostrazione originale di Viète che utilizza il metodo geometrico simile a quello utilizzato da Archimede per calcolare l’area del cerchio e la lunghezza della circonferenza (chiamato anche metodo di esaustione, che anticipa di diversi secoli il calcolo integrale sviluppato da Newton e Leibniz nel Seicento).
Dimostrazione geometrica della formula di Viète
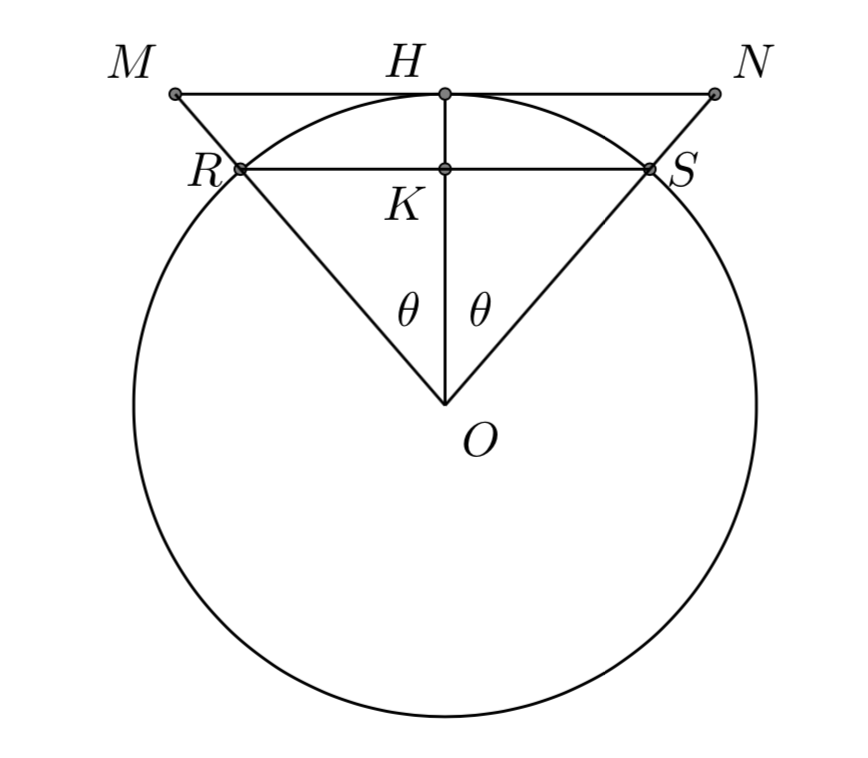
Supponiamo di avere un poligono regolare di \( n \) lati inscritto in un cerchio di raggio uguale a 1, con angolo al centro uguale a \( 2\theta \). Se raddoppiamo il numero dei lati, il poligono regolare di \( 2n \) lati ha angolo al centro uguale a \( \theta \). Come è noto dalla trigonometria l’area del triangolo \( \bigtriangleup ORS \) è uguale a \( \frac{1}{2}\sin 2\theta = \sin \theta \cdot \cos \theta \). Le aree \( A_n \) e \( A_{2n} \) dei poligoni regolari di \( n \) e \( 2n \) lati sono quindi date dalle seguenti formule:
\[ \begin{array}{ll} A_{n} = n\sin \theta \cos \theta \\ A_{2n}= 2n \sin \frac{\theta}{2} \cos \frac{\theta}{2} \end{array} \\ \]Da queste due formula si ricava subito la seguente relazione:
\[ A_{n}=A_{2n}\cos \theta \\ \]Supponiamo ora di partire con un quadrato inscritto nel cerchio: \( n=4 \), \( \theta=\frac{\pi}{4} \). Iterando la relazione precedente troviamo la seguente formula:
\[ A_{4}=2=A_{2^{n+1}}\cos \frac{\pi}{4}\cos \frac{\pi}{8} \cdots \cos \frac{\pi}{2^{n}} \\ \]Poiché il limite \( \lim\limits_{n \to \infty}A_{2^{n+1}}=\pi \) è l’area del cerchio di raggio unitario, abbiamo di nuovo la formula di Viète.
3) Il prodotto infinito di Wallis
John Wallis (1616-1703) pubblicò la formula per \( \pi \) nella sua opera più importante Arithmetica infinitorum, pubblicata nel 1656:
\[ \frac{\pi}{2}=\frac{2 \cdot 2 \cdot 4 \cdot 4 \cdot 6 \cdot 6} {1\cdot 3 \cdot 3\cdot 5 \cdot 5\cdot 7}\cdots = \prod_{n=1}^{\infty}\frac{4n^{2}}{4n^{2}-1} \\ \]La formula di Wallis è un grande risultato dal punto di vista teorico, in quanto per la prima volta ha rappresentato il numero \( \pi \) come limite di una successione di numeri razionali, mentre la formula di Viète utilizza i numeri irrazionali. Tuttavia ai fini del calcolo delle cifre la formula di Wallis è poco utile, in quanto converge lentamente.
La classica dimostrazione utilizza le seguenti formule, valide per \( n >0 \):
Lemma 3.1 – Integrali di Wallis
\[ \begin{array}{l} \int\limits_{0}^{\frac{\pi}{2}}\sin ^{2n}xdx =\int\limits_{0}^{\frac{\pi}{2}}\cos ^{2n}xdx= \frac{1\cdot 3\cdots (2n-1)}{2\cdot 4\cdots (2n)}\frac{\pi}{2} \\ \int\limits_{0}^{\frac{\pi}{2}}\sin ^{2n+1}xdx =\int\limits_{0}^{\frac{\pi}{2}}\cos ^{2n+1}xdx= \frac{2\cdot 4\cdots (2n)}{1\cdot 3\cdots (2n+1)} \end{array} \\ \]Dimostrazione
Poniamo \( I_{n}=\int_{0}^{\frac{\pi}{2}}\sin^{n}x dx \). In primo luogo dimostrare che \( I_{0}=\frac{\pi}{2} \) e \( I_{1}=1 \). Quindi effettuare l’integrazione per parti e ricavare la seguente formula ricorsiva:
Utilizzando i valori iniziali \( I_{0},I_{1} \) si trovano quindi le formule generali nel caso pari e nel caso dispari.
Mediante questi integrali la formula di Wallis può essere dimostrata osservando che possiamo scrivere la seguente relazione:
\[ \frac{\pi}{2} =\frac{I_{2n}}{I_{2n+1}}\prod_{k=1}^{n}\frac{4k^{2}}{4k^{2}-1} \\ \]A questo punto per dimostrare la formula di Wallis basta dimostrare che
\[ \lim_{n \to \infty}\frac{I_{2n}}{I_{2n+1}}=1 \]Esercizio 3.1
Dimostrare la seguente formula:
4) La formula di Eulero per il seno
Nel 1734 Eulero scoprì la seguente formula:
\[ \frac{\sin \pi x}{\pi x} = \prod_{n=1}^{\infty}\left(1- \frac{x^{2}}{n^{2}}\right) \\ \]La formula vale per qualunque numero reale o complesso. In questo articolo ci limitiamo a considerare il caso di x numero reale.
Notiamo che ponendo \( x=\frac{1}{2} \) abbiamo la formula di Wallis.
Presentiamo inizialmente il ragionamento euristico con cui Eulero scoprì la formula. Per questo ricordiamo la seguente proprietà dei polinomi:
Teorema 4.1
Sia dato un polinomio \( p(x) \) di grado \( n \). Un numero reale \( r \) è uno zero del polinomio se e solo se \( p(x)=(x-r)q(x) \), dove \( q(x) \) è un polinomio di grado \( n-1 \).
Esempio 4.1
Un polinomio che ha come zeri \( 4 \) e \( -2 \) è il seguente: \( p(x)=C(x-4)(x+2) \), dove \( C \) è una costante arbitraria diversa da zero.
La funzione \( \displaystyle \frac{\sin x}{ x} \) ha il seguente sviluppo in serie di Taylor:
\[ \frac{\sin x}{ x} = 1 – \frac{x^{2}}{3!}+ \frac{x^{4}}{5!} – \cdots \\ \]Il ragionamento euristico di Eulero consiste nel considerare gli zeri della funzione \( \displaystyle \frac{\sin \pi x}{\pi x} \), trattata come se fosse un polinomio con infiniti termini. Esistono infiniti zeri \( x=\pm 1, \pm 2, \cdots \). Potremo quindi scrivere:
\[ \frac{\sin \pi x}{\pi x}= C(1-x^{2})(1-\frac{x^{2}}{4})(1-\frac{x^{2}}{9}) \dots \\ \]Il prodotto infinito converge per tutti i valori di \( x \) e ha gli stessi zeri della funzione \( \displaystyle \frac{\sin \pi x}{\pi x} \). Affinché le due funzioni siano uguali deve essere \( C=1 \). Infatti abbiamo
\[ \lim\limits_{x \to 0}\frac{\sin \pi x}{\pi x}=1 \\ \]Il ragionamento di Eulero non può essere considerato una vera dimostrazione, in quanto la funzione \( \displaystyle \frac{\sin \pi x}{\pi x} \) non è un polinomio, e inoltre il numero dei zeri è infinito. Tuttavia, come spesso accade in matematica, un teorema prima viene intravisto dai matematici e poi in seguito dimostrato in modo rigoroso.
Oggi il teorema di Eulero si dimostra facilmente mediante il famoso Teorema di fattorizzazione di Weierstrass, il quale afferma sostanzialmente che ogni funzione analitica di variabile complessa può essere espressa come prodotto finito o infinito che coinvolge i suoi zeri. Per i dettagli vedere un testo di analisi complessa, ad esempio il libro di Lang[3].
È possibile dimostrare la formula di Eulero senza ricorrere all’analisi complessa, ad esempio ricorrendo all’analisi di Fourier. L’analisi di Fourier è lo studio della rappresentazione di funzioni generiche come somme di funzioni trigonometriche seno e coseno, con frequenze specifiche. Si tratta di un argomento molto vasto e fondamentale in vari settori della matematica, della fisica e di altre scienze applicate.
Lo sviluppo in serie di Fourier (1768-1830) vale sotto diverse condizioni della funzioni. Ricordiamo soltanto il teorema fondamentale nel caso di una funzione continua. Per uno studio approfondito dell’analisi di Fourier consultare ad esempio il testo di Spiegel[4].
Teorema 4.2 – Fourier
Sia data una funzione \( f(x) \) continua e periodica nell’intervallo \( [-L,L] \). Allora la funzione può essere rappresentata con il seguente sviluppo in serie di Fourier:
dove
\[ \begin{array}{l} a_{0} =\frac{1}{L} \int\limits_{-L}^{L}f(x)dx \\ a_{n} =\frac{1}{L} \int\limits_{-L}^{L}f(x)\cos(\frac{n\pi x}{L})dx \\ b_{n} =\frac{1}{L} \int\limits_{-L}^{L}f(x)\sin(\frac{n\pi x}{L})dx \end{array} \\ \]Esercizio 4.1
Dimostrare che se la funzione è pari, cioè \( f(-x)=f(x) \) allora \( b_{n}=0 \). Se invece la funzione è dispari, cioè \( f(-x)=-f(x) \) allora \( a_{n}=0 \).
Esercizio 4.2
Trovare lo sviluppo in serie di Fourier per la funzione \( f(x)=\cos (tx) \), con \( t \ne 0, \pm 1 \, \pm 2, \cdots \) e \( -\pi \le x \le \pi \).
Soluzione
Si tratta di una funzione pari, in quanto \( \cos(-x)=\cos(x) \) e quindi \( b_{n}=0 \). Per trovare lo sviluppo di Fourier bisogna quindi calcolare il coefficienti \( a_{0} \) e \( a_{n} \). Effettuando i calcoli si trova il seguente sviluppo in serie:
A questo punto possiamo dare una nuova dimostrazione della formula di Eulero.
In base all’esercizio precedente, ponendo \( x=\pi \), e ricordando che \( \displaystyle \cot x = \frac{\cos x}{\sin x} \), possiamo scrivere:
La serie a destra converge uniformemente in ogni intervallo \( 0 \le t <1 \) e quindi è possible effettuare l’integrazione per serie. L’integrale a sinistra è:
\[ \int\limits_{0}^{x}\left(\pi \cot t\pi – \frac{1}{t}\right)dt = \left. \ln \left(\frac{\sin \pi t}{\pi t}\right) \right]^x_0 \\ \]L’integrazione della serie a destra è un po’ laboriosa, ma non difficile. Completando i calcoli otteniamo la formula di Eulero:
\[ \frac{\sin \pi x}{\pi x}= \left(1-\frac{x^{2}}{1^{2}}\right)\left(1-\frac{x^{2}}{2^{2}}\right) \cdots \\ \]Esercizio 4.3
Dimostrare la seguente formula
Suggerimento
Utilizzare la formula di Eulero per il seno e la relazione \( \sin 2x = 2 \sin x \cos x \).
Conclusione
Il numero \( \pi \) non ha solo un ruolo centrale nella storia della matematica, ma riguarda la storia della cultura umana nelle sue diverse espressioni: fisica, astronomia, arte, architettura, letteratura, ecc. La sua importanza venne riconosciuta già dai Babilonesi e poi dagli Egiziani, migliaia di anni fa. Per una panoramica storica vedere ad esempio il libro edito da Springer[5], oppure il libro di Beckmann[6].
In un prossimo articolo studieremo altre rappresentazioni del numero \( \pi \), in particolare tramite le serie infinite, che grazie all’ausilio di computer potenti, permettono di calcolare velocemente un grande numero di cifre decimali.
Bibliografia
[1]T. Apostol – Mathematical Analysis (Pearson)
[2]K. Knopp – Theory and Application of Infinite Series (Dover)
[3]S. Lang – Complex Analysis (Springer-Verlag)
[4]M. Spiegel – Schaum’s Outline of Fourier Analysis with Applications to Boundary Value Problems (McGraw-Hill)
[5]J. L. Berggreen, J. Borwein, P. Borwein – Pi: A Source Book (Springer)
[6]P. Beckmann – A History of Pi (St. Martin’s Press, 1976)
0 commenti